Relaciones lógicas y dependientes de electrones de valencia fuertes de impurezas elementales en semiconductores binarios 2D:un caso de monocapa GeP3 de estudios ab initio

Resultados y discusiones

Oscilaciones pares-impares para sistemas de dopaje de elemento único

La Figura 1a muestra la vista superior y lateral de la estructura del GeP ₃ Supercélula 2 × 2, y la Fig. 1b es la zona de Brillouin 2D correspondiente de GeP ₃ monocapa. Las constantes de celosía optimizadas de GeP ₃ monocapa son \ (\ mathrm {a} =\ mathrm {b} =6,96 \ {\ AA} \), y la banda prohibida calculada es de aproximadamente 0,26 eV, lo que concuerda con otros cálculos teóricos.

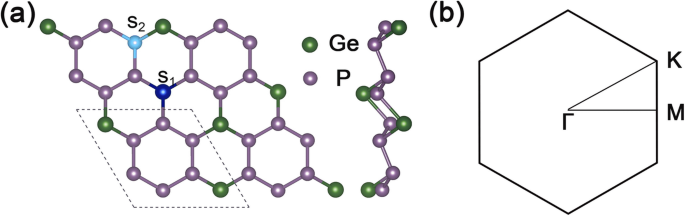
Estructura geométrica y zona de Brillouin de GeP ₃ . un Vistas superior y lateral de la geometría optimizada de GeP ₃ con una supercélula de 2 × 2. La línea de puntos presenta la celda unitaria de GeP ₃ monocapa, S ₁ representa el sitio de la posición de sustitución del sitio Ge, y S ₂ representa el sitio de sustitución del átomo de posición P. b la zona 2D Brillouin de GeP ₃ monocapa

En primer lugar, trazamos las estructuras de bandas de GeP ₃ dopado con un solo elemento monocapa con un átomo de Ge de sustitución (aquí, elegimos B, C, N, O, Al, Si, P, S, Ga, As y Se como dopantes). Los resultados se muestran en la Fig. 2a-1, respectivamente. Podemos ver claramente que el nivel de Fermi aumenta y cruza las bandas de conducción para el grupo V (N, P, As) debido a un dopante de electrones más, mientras que para los dopantes del grupo III (B, Al, Ga) debido a un electrón menos, el uno se desplaza hacia abajo y cruza las bandas de valencia. Por ejemplo, en la Fig. 2f yj, el máximo de su banda de valencia solo corresponde a las bandas parcialmente ocupadas que se muestran en la Fig. 2e e i. Sin embargo, para los dopantes del grupo IV (C, Si y Ge) y VI (O, S y Se), debido al mismo o dos electrones más que el átomo de Ge, los sistemas exhiben una característica semiconductora. Tal sintonía de la transición semiconductora a metálica proviene de la ocupación del número de electrones de valencia, es decir, la ocupación de electrones de valencia impares (pares) conduce a propiedades metálicas (semiconductoras).

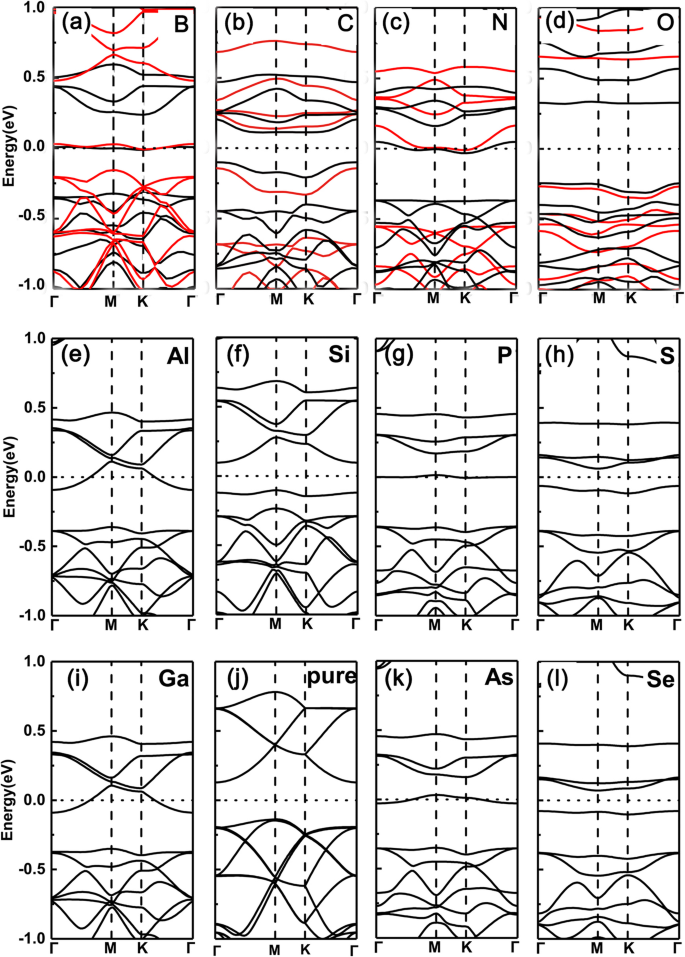
Estructuras de bandas de los diversos dopantes en GeP ₃ monocapa con sustitución del átomo de Ge. un B, b C, c N, d O, e Al, f Si, g P, h S, yo Ga, j Pure GeP ₃ , k Como, l Se. Estructuras de bandas calculadas para una supercélula \ (\ mathsf {2} \ times \ mathsf {2} \) con varios dopantes en GeP ₃ monocapa del grupo III al VI, sustituyendo el átomo de Ge, respectivamente, junto con el de GeP ₃ puro monocapa. Tanto las funciones PBE como HSE06 se emplean en la fila superior

Para confirmar la validez de los resultados anteriores derivados de las funciones PBE, también empleamos las funciones funcionales de densidad híbrida (HSE06) para verificar los sistemas dopados de la fila superior. Está claro que los funcionales de PBE de hecho dan los errores de los huecos de banda debido a la subestimación. Sin embargo, en nuestros sistemas estudiados, todos ellos tienen brechas considerables, esto significa que los errores entre las propiedades metálicas o semiconductoras causados ​​por los funcionales PBE generalmente no sucederán (Esto se debe a que en algunas brechas de banda pequeñas de los semiconductores, los funcionales PBE generalmente dan lugar al error entre propiedades conductoras y metálicas). Además, en nuestro estudio, lo que nos preocupa son las características metálicas o semiconductoras, en lugar de los valores específicos de los espacios de banda. En comparación con las brechas derivadas de las funciones PBE, las brechas de las funciones HSE06 aumentan claramente. Incluso con estos, las oscilaciones de semiconductores de metal permanecen intactas. Por lo tanto, los ingredientes centrales extraídos en base a las funciones de PBE son confiables.

Sin embargo, en marcado contraste, los casos de sustitución de átomos de P por los mismos dopantes están totalmente invertidos, como se muestra en la Fig. 3a-1, respectivamente. Es decir, para los dopantes del grupo V (N, As) y del grupo III (B, Al, Ga), los sistemas dopados siguen siendo propiedad semiconductora, mientras que para los grupos IV (C, Si, Ge) y VI (O, S, Se) dopantes, los que cambian a características metálicas (aquí, la misma tendencia también se encuentra entre los funcionales PBE y HSE06). Esto se debe a que los electrones de valencia se mantienen iguales (dos menos) que (que) la GeP ₃ intrínseca para los dopantes del grupo V (grupo III), pero un electrón menos (más) para los dopantes del grupo IV (VI).

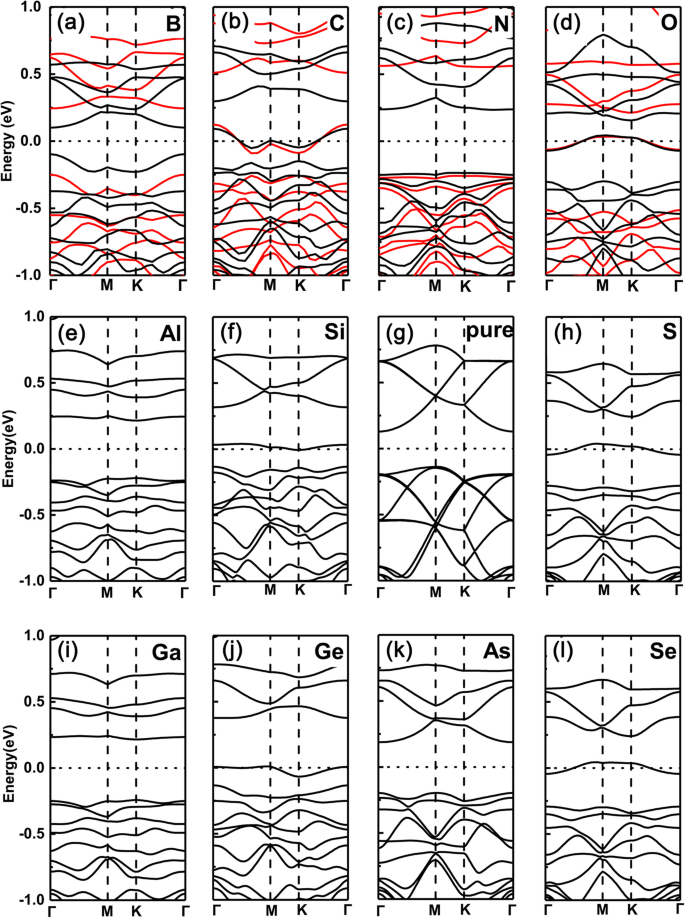
Estructuras de bandas de los diversos dopantes en GeP ₃ monocapa con un átomo de P sustituido. un B, b C, c N, d O, e Al, f Si, g P, h S, yo Ga, j Pure GeP ₃ , k Como, l Se. Estructuras de bandas calculadas para una supercélula \ (\ mathsf {2} \ times \ mathsf {2} \) con varios dopantes en GeP ₃ monocapa del grupo III al VI, con átomos de P sustituidos, respectivamente, junto con el de GeP ₃ puro monocapa. Tanto las funciones PBE como HSE06 se emplean en la fila superior

Para presentar mejor las oscilaciones de la transición de propiedades semiconductoras a metálicas, trazamos la tendencia cambiante de la banda prohibida como los diferentes dopantes, como se muestra en la Fig. 4a yb, respectivamente. Claramente, podemos ver que la transición de propiedades semiconductoras a metálicas se está invirtiendo drásticamente. Específicamente, las oscilaciones metálicas (semiconductoras) -semiconductoras (metálicas) ocurren en la sustitución del sitio Ge (P) como los dopantes que van del grupo III al VI. Además, también encontramos un fenómeno interesante que muestra que la magnitud de la banda prohibida casi se mantiene igual que la intrínseca GeP ₃ monocapa cuando los dopantes tienen los mismos electrones de valencia que el átomo de Ge. Sin embargo, cuando los dopantes tienen dos electrones más que el átomo de Ge, la magnitud de los espacios entre bandas cambia relativamente más. Sin embargo, para los dopantes en los sitios P, independientemente del número de electrones de valencia, la magnitud de los huecos de banda siempre cambia relativamente grandemente. Esto puede entenderse por el efecto conjunto del radio del átomo y los electrones de valencia disponibles, es decir, los dopantes con casi el mismo radio (menor o mayor) y electrones de valencia que (que) el átomo de Ge causan un efecto relativamente menor (mayor) en la electrónica. propiedades, como la banda prohibida. Esto significa que uno puede ajustar no solo las oscilaciones de las transiciones semiconductoras-metálicas, sino que también puede ajustar la magnitud de la banda prohibida eligiendo los dopantes adecuados y los diferentes sitios de dopaje.

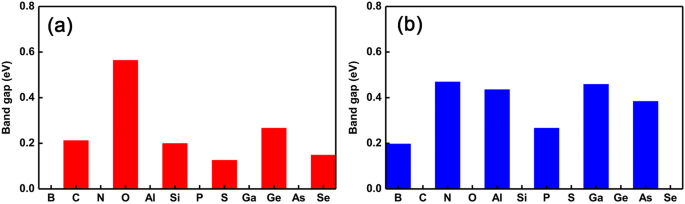
Huecos de banda de todos los sistemas con un solo dopado. Huecos de banda de GeP ₃ dopado monocapas con los diferentes dopantes que van desde el grupo V al VI. un la sustitución de átomos de Ge y b los átomos de sustitución de P, respectivamente

Para comprender el cambio de las estructuras electrónicas de diferentes dopantes en el GeP ₃ monocapa, graficamos la densidad parcial de estados (PDOS) del grupo intrínseco y de dopaje IV-V en GeP ₃ monocapa, como se muestra en la Fig. 5a – d, respectivamente. Se puede ver claramente que la banda de valencia máxima (VBM) y la banda de conducción mínima (CBM) del GeP ₃ La monocapa proviene principalmente de orbitales p de átomos de Ge y P. Cuando los dopantes con el mismo número de electrones de valencia que el átomo de Ge, como C y Si, estén disponibles, habrá estados de impureza que se ubicarán justo por encima del VBM de la GeP intrínseca ₃ monocapa porque el nivel de energía orbital p de C y Si es más alto que el del átomo de P (ver Fig. 5a). Por lo tanto, la propiedad conductora está intacta y la magnitud del cambio de banda prohibida es relativamente pequeña. Sin embargo, cuando los dopantes tienen un electrón más que el átomo de Ge, como N, P y As, también habrá estados de impureza en la banda prohibida y los estados de impureza se originan a partir de la hibridación de CBM dividido (dominante) y los estados de dopantes (ver Fig. 5b).

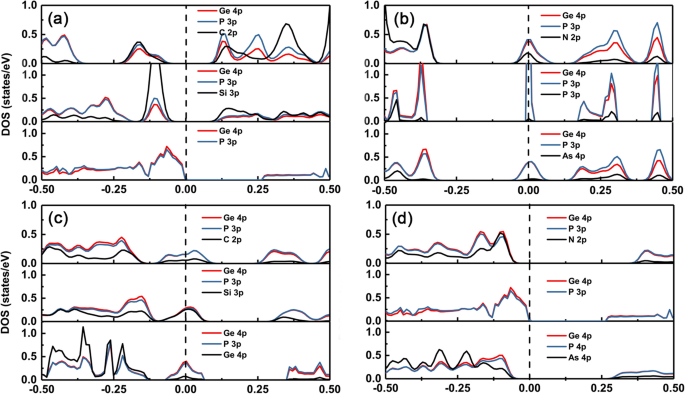
DOS para los sistemas dopados. La densidad parcial de estados (derecha) para los átomos del grupo IV (C, Si y Ge) y del grupo V (N, P y As) dopados con GeP ₃ . La línea discontinua vertical ennegrecida es el nivel de Fermi. (a) y (b) átomo de Ge sustituido, (c) y (d) átomo de P sustituido

Por el contrario, para el dopaje en el sitio P, cuando los dopantes tienen un electrón de valencia menos que el átomo de P, como el grupo IV, habrá estados de impureza en el nivel de Fermi, y los estados de impureza se componen de VBM dividido (dominante ) y los estados de los dopantes. Mientras que, cuando los dopantes tienen el mismo número de electrones de valencia que el átomo de P, como el grupo V, los sistemas dopados aún mantienen una característica semiconductora (ver Fig. 5c). Los huecos de banda se vuelven relativamente más grandes que el de GeP ₃ intrínseco monocapa debido al mayor desajuste de las constantes reticulares. Además, también observamos que la banda prohibida del dopante N es mayor que la del dopante As en la sustitución de átomos de P. Esto se debe a que el nivel de energía del orbital p del átomo de As es más alto que el del átomo de N, por lo tanto, cuanto mayor es el nivel de energía del orbital p, mayor es el desplazamiento hacia arriba de los estados de impureza lejos de VBM (ver Fig. 5d).

Relaciones lógicas para sistemas de codopaje

Sobre la base de los hallazgos antes mencionados de los diferentes dopantes individuales, por lo tanto, podemos diseñar sistemas de codopaje para satisfacer las propiedades electrónicas que deseamos. Aquí, solo mostramos los resultados de B, C, N y O como ejemplos para ilustrar el efecto de codopaje, pero la conclusión es sólida frente a los diferentes dopantes seleccionados. Por ejemplo, en el codopaje del sitio Ge, los dos dopantes con un electrón de valencia menos pueden conducir naturalmente a la propiedad semiconductora, mientras que para los dos dopantes con un número cada vez menor de electrones de valencia, los sistemas de codopaje también pueden tienen una propiedad semiconductora.

Sin embargo, para los dos dopantes con uno menos (más) y el mismo electrón de valencia, los sistemas de co-dopaje aún mantienen la propiedad metálica ya que un número menor (más) de dopantes de electrones de valencia resultó como propiedad. Simplificando, esta idea está exactamente confirmada por nuestros cálculos adicionales de la teoría funcional de densidad (DFT) de sistemas co-dopados, vea los resultados en la Fig. 6a-l para las estructuras de banda de B, C, N y O co-dopado GeP ₃ monocapa.

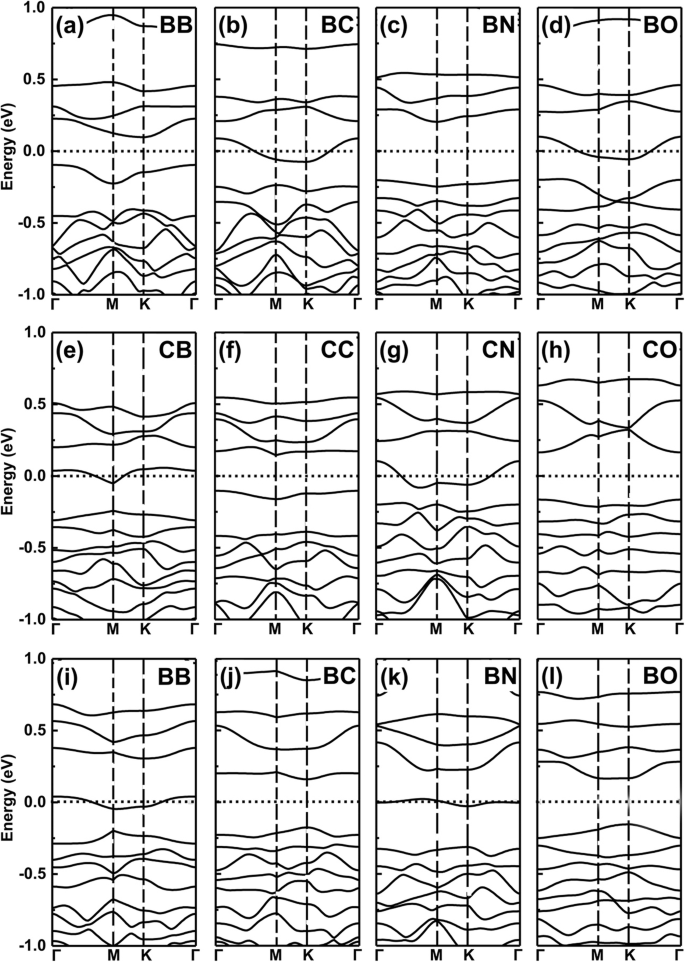
Estructuras de bandas de sistemas codopados. Las estructuras de bandas de B, C, N y O codoparon GeP ₃ monocapa. un - d Los dos dopantes sustituyen dos átomos de Ge en GeP ₃ monocapa, e - h los dos dopantes sustituyen dos átomos de P, i - l los dos dopantes sustituyen un átomo de Ge y un átomo de P, respectivamente

Ahora, podemos dar un ejemplo de operación lógica "Y", estableciendo la propiedad metálica como "M" y la característica semiconductora como "S". Definimos las relaciones lógicas:M AND M =S, S AND S =S, y M AND S =M, respectivamente. En este documento, estos hallazgos que hemos obtenido anteriormente obedecen a relaciones de tipo lógico, por ejemplo, los dopantes con un electrón de valencia más y uno menos dan como resultado una propiedad metálica, pero cuando usamos los dos dopantes como codopaje, como B y N en los sitios Ge como se muestra en la Fig. 7a yb, los sistemas codopados se convierten en propiedad semiconductora como se esperaba ver Fig. 6c. Si elegimos B-C co-dopado GeP ₃ sistema monocapa, presenta característica metálica como es el caso de M y S (ver Fig. 4a, b). Lo mismo para los átomos C-N, N-O y B-O que se dopan conjuntamente en GeP _3, sustituyendo dos átomos de Ge, dos átomos de P o un átomo de Ge y P, como se muestra en la Fig. 7c – f, respectivamente.

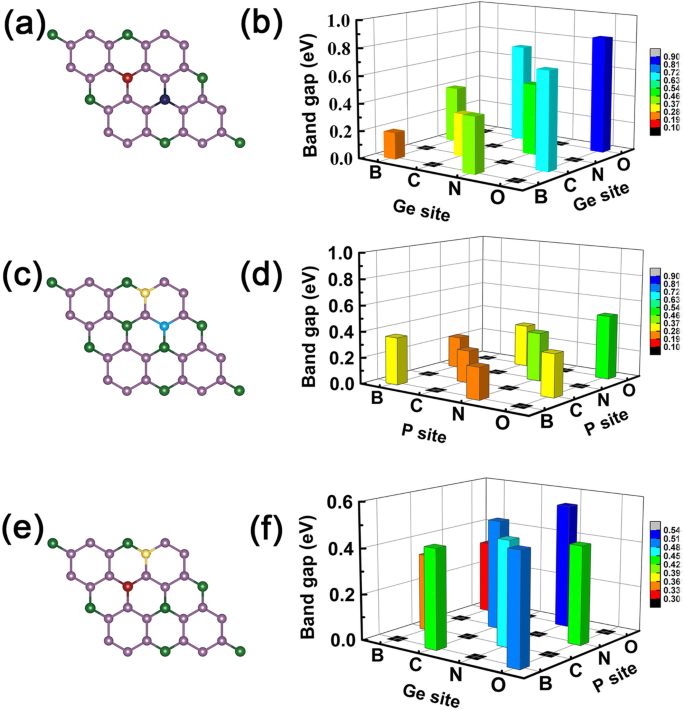
Band gap de todos los sistemas codopados. La magnitud de los huecos de banda de GeP ₃ co-dopado monocapa, las izquierdas son el boceto de los sitios co-dopados, y los derechos son la magnitud de los huecos de banda correspondientes a los elementos de dopaje. un , b El caso de los elementos de dopaje ocupan los dos átomos de Ge. c , d El caso de los elementos de dopaje ocupan los dos átomos de P. e , f El caso de los elementos de dopaje ocupan los átomos de Ge y P, respectivamente

Finalmente, verificamos la estabilidad tanto de los sistemas de un solo dopado como de los codopados para asegurarnos de que se puedan realizar más en el experimento. La energía de formación se calcula usando las Ecs. (1) y (2) para casos de dopaje simple y de dopaje conjunto, respectivamente. Los resultados están presentes en la Fig. 8a-e. De la Fig. 8a yb, podemos ver claramente que el E _f de los dopantes individuales en los sitios Ge son todos cercanos a los de GeP ₃ monocapa (puesta a cero como punto de referencia), excepto los átomos de C, N y S. También notamos que, para los dopantes de átomos B, O, P, Ge y Se, las energías de formación son mucho más pequeñas que las de otros dopantes, lo que indica que son muy fáciles de dopar en un experimento. Para los dopantes en los sitios P, los dopantes de átomos de B, O, P y Ge tienen una energía de formación relativamente menor y también son fáciles de dopar. C, N, Al y Ga no son fáciles de dopar.

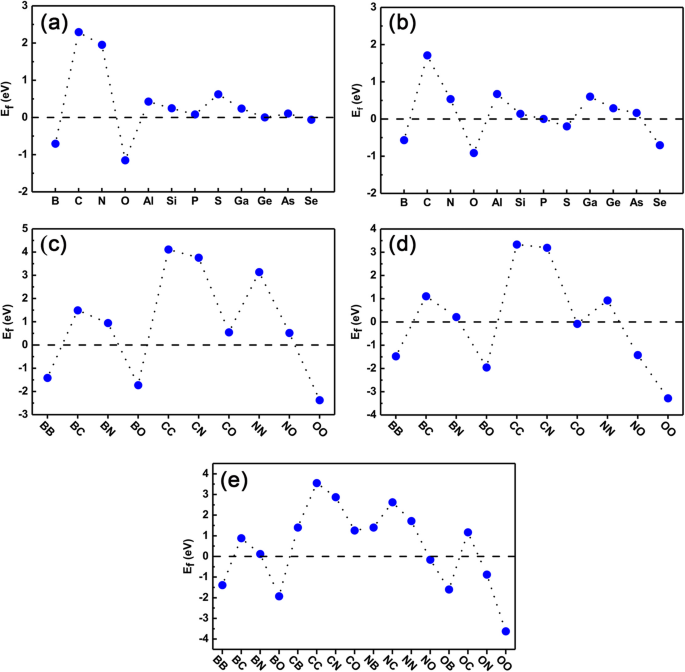
Energía de formación de todos los sistemas dopados. La energía de formación calculada de los sistemas de dopaje y codopaje de un solo elemento. un , b son el átomo de Ge y el átomo de P sustituidos con dopante, respectivamente; c - e Los codopantes sustituidos por dos átomos de Ge, dos átomos de P y un átomo de Ge y un átomo de P, respectivamente

En cuanto a la energía de formación del codopaje, las Fig. 8c-e son la energía de formación del codopaje donde dos dopantes ocupan las posiciones de dos átomos de Ge (indicados como sitios Ge-Ge), dos átomos de P (indicados como PP sitios), un átomo de Ge y un átomo de P (denotados como sitios Ge-P), respectivamente. Aquí solo mostramos los resultados de los dopantes de B, C, N y O como ejemplo. Para los sitios Ge-Ge y los sitios P-P, la energía de formación del codopaje se puede estimar de forma aproximada promediando las energías de formación del dopaje de un solo elemento por separado. Claramente, para el codopaje BB, BO y OO en sitios Ge-Ge y el codopaje BB, BO, NO y OO en sitios P-P, las energías de formación son relativamente pequeñas y pueden realizarse fácilmente en el experimento. Sin embargo, para el dopaje CC, CN y NN en los sitios Ge-Ge y el dopaje CC y CN en los sitios P-P, las energías de formación son relativamente mayores, lo que indica que son difíciles de dopar en el experimento. Para el codopaje de sitios Ge-P, como se muestra en la Fig. 8e, la energía de formación se vuelve más compleja que el codopaje de sitios Ge-Ge o P-P porque hay transferencia de carga entre los dopantes. En cualquier caso, el codopaje BB, BO y OO tienen energías de formación más pequeñas, mientras que el codopaje CC, CN y NN tienen energías de formación más grandes. En general, la energía de formación depende en gran medida del número de electrones de valencia del dopante. Específicamente, cuando los dos dopantes tienen un electrón menos (más) que los átomos sustituidos, la energía de formación del sistema codopado es menor (mayor) que la de los dopantes individuales correspondientes, como los sitios de Ge codopados BB (NN). Esto se debe a que existe una competencia entre la energía disminuida (aumentada) de los electrones reducidos (aumentados) de los sistemas dopados y la repulsión de Coulomb. Para el codopaje agujero-agujero, la energía del primer caso es mucho mayor que la del último caso, lo que resulta en una energía de formación bastante disminuida en sistemas de codopaje como BB, mientras que para el codopaje electrón-electrón, ambos los casos anteriores y posteriores conducen a la energía de formación superior, como NN. Sin embargo, para los sistemas codopados con huecos y electrones, como los sitios de Ge codopados con BN, la energía de formación es dramáticamente más baja que en los casos con un solo dopado correspondiente. Esto se debe a que en dicho sistema codopado, no hay ganancia de energía de los electrones netos añadidos o reducidos en los sistemas, y la interacción de Coulomb juega un papel decisivo en la formación de los codopantes. En total, tomando en conjunto nuestros estudios previos de dopaje de elementos en fosforeno negro, cabe señalar que nuestros estudios actuales tienen un cierto grado de universalidad y se espera que apliquen otras monocapas de semiconductores 2D, como BN, MoS _{2 ,} y así sucesivamente.

Finalmente, para comprobar la estabilidad de los sistemas dopados anteriores en comparación con el caso no dopado, llevamos a cabo el AIMD (dinámica molecular ab initio) para mostrar la energía frente al tiempo, como se muestra en la Fig. 9a-f. Podemos ver claramente que la amplitud oscilatoria será convergente siempre que el tiempo dure lo suficiente (~ 4 ps), lo que implica que los sistemas dopados no colapsarán contra fluctuaciones térmicas de hasta 300 K para GeP dopado C ₃ en la Fig. 9a. Incluso para el GeP ₃ dopado con átomo de C más activo , la temperatura extrema puede ser de hasta 300 K, como se muestra en la Fig. 9c. Además, también tomamos como ejemplo la sustitución del metal Al en el sitio Ge, el resultado calculado se muestra en la Fig.9e yf, de lo cual podemos ver claramente que la amplitud de oscilación de energía disminuye gradualmente con el tiempo que dura, lo que significa que la energía podría ser convergente siempre que el tiempo dure lo suficiente y la estructura del sistema dopado sea térmicamente estable frente a la fluctuación térmica. Por lo tanto, podemos esperar que tales sistemas dopados se puedan realizar en experimentos adicionales dado el GeP ₃ de alta calidad se prepara la monocapa.

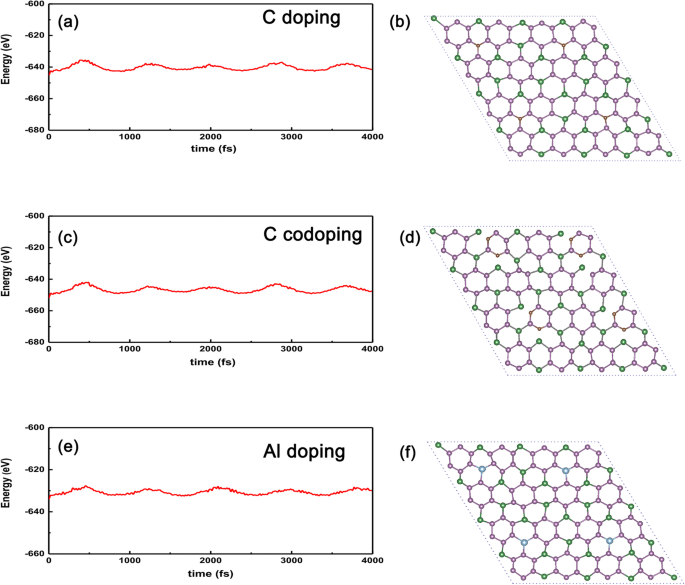
AIMD para los sistemas dopados con átomos de C, dos C y Al. AIMD confirma la estabilidad térmica de a GeP ₃ dopado con átomo de C sustituyendo átomo de Ge, c dos átomos de C dopados con GeP ₃ sustituyendo dos átomos de P, y e GeP ₃ dopado con átomos de Al con sustitución a 300 K. Las estructuras en b C, d dos átomos de C y f Al corresponden a sus estructuras finales después de 4000 fs

Al final, queremos discutir la confiabilidad de nuestro estudio presentado aquí. Nuestras conclusiones presentadas aquí son resultados pronosticados teóricamente pero son altamente confiables. Esto se debe a que se ha informado sobre nuestro material anfitrión utilizado aquí y su fase masiva de capas GeP ₃ ya existe [26]. Por lo tanto, nuestros fenómenos relacionados inducidos por el dopaje estudiados deben confirmarse aún más en el experimento una vez que la monocapa GeP ₃ se realiza aún más. Luego, se podría realizar el dopaje de los átomos correspondientes. Por simplicidad, dopaje de electrones o huecos en monocapa GeP ₃ podría realizarse mediante la adsorción de algunas moléculas.