Dependencia de las propiedades electrónicas y ópticas de las multicapas MoS2 en el acoplamiento entre capas y la singularidad de Van Hove
Resumen
En este artículo, las propiedades estructurales, electrónicas y ópticas de MoS 2 las multicapas se investigan empleando el método de los primeros principios. Hasta seis capas de MoS 2 han sido estudiados comparativamente. La covalencia y la ionicidad en el MoS 2 se ha demostrado que las monocapa son más fuertes que las de la masa. A medida que el número de capas aumenta a dos o más de dos, la división de bandas es significativa debido al acoplamiento entre capas. Descubrimos que surgían mesetas largas en las partes imaginarias de la función dieléctrica \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) y la densidad conjunta de estados (JDOS) de MoS 2 multicapas, debido a las singularidades de Van Hove en un material bidimensional. Aparecen uno, dos y tres pequeños pasos en los umbrales de la meseta larga de \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) y JDOS, para monocapa, bicapa y tricapa, respectivamente . A medida que aumenta el número de capas, el número de pequeños pasos aumenta y el ancho de los pequeños pasos disminuye en consecuencia. Debido al acoplamiento entre capas, la meseta más larga y la meseta más corta de JDOS son de la monocapa y a granel, respectivamente.
Introducción
Disulfuro de molibdeno (MoS 2 ) es uno de los dicalcogenuros de metales de transición típicos y se ha utilizado ampliamente como catalizador [1] y como material de almacenamiento de hidrógeno [2, 3]. Debido a las fuertes interacciones en el plano y las débiles interacciones de van der Waals entre MoS 2 capas atómicas [4, 5], MoS 2 Los cristales son conocidos desde hace muchos años como un importante lubricante sólido [6, 7]. La monocapa MoS 2 , el llamado 1 H -MoS 2 , se ha exfoliado de MoS 2 a granel mediante el uso de escisión micromecánica [8]. El llamado 2 H -MoS 2 (entre 1T , 2H , 3R ) es la estructura más estable de MoS a granel 2 [9, 10] y es un semiconductor con una banda prohibida indirecta de 1,29 eV [4, 11, 12]. La monocapa MoS 2 También ha llamado mucho la atención debido a su naturaleza bidimensional y su estructura de panal de abeja similar al grafeno. Es interesante que la monocapa MoS 2 tiene una banda prohibida directa de 1,90 eV [4, 13] que se puede utilizar como canal conductor de transistores de efecto de campo [14]. Por otro lado, la banda prohibida cero del grafeno restringe sus aplicaciones en óptica y aplicaciones de transistores [15,16,17,18]. Además, los trabajos teóricos y experimentales muestran que la banda prohibida electrónica disminuye a medida que el número de MoS 2 capas aumenta [19,20,21,22]. Acoplamiento entre capas de MoS 2 multicapa es sensible al espesor de la capa [21]. Algunas investigaciones sobre el MoS multicapa 2 están disponibles [19,20,21,22,23,24,25]; sin embargo, las estructuras electrónicas y las propiedades ópticas del MoS 2 multicapa todavía no están bien establecidas, especialmente para las propiedades físicas dependientes de la capa relacionadas con el acoplamiento entre capas. La singularidad de Van Hove (VHS) juega un papel importante en las propiedades ópticas [26, 27]. Los únicos puntos críticos disponibles en materiales bidimensionales son los del P 0 ( P 2 ) y P 1 type, que se muestran como un paso y una singularidad logarítmica [26, 27]. En este artículo, analizamos las propiedades electrónicas y ópticas de MoS 2 relacionados con la singularidad de Van Hove, capa por capa y hasta seis capas atómicas.
En la actualidad, se han realizado con éxito cálculos de primeros principios para estudiar las propiedades estructurales, electrónicas y ópticas de una amplia variedad de materiales. En este trabajo, hemos estudiado sistemáticamente las propiedades electrónicas y ópticas de MoS monocapa, multicapa y a granel 2 utilizando cálculos ab initio. Se enfatizan las discusiones sobre las propiedades ópticas. Nuestros resultados muestran que, para E || x , las partes imaginarias de la función dieléctrica \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) poseen mesetas largas. En estos umbrales de estas mesetas, \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) de la monocapa, bicapa y tricapa exhiben uno, dos y tres pequeños pasos, respectivamente. La parte imaginaria de la función dieléctrica también se analiza mediante la densidad conjunta de estados y los elementos de la matriz de transición. JDOS combinado con las estructuras de banda y las singularidades de Van Hove se discuten en detalle.
Métodos
Los cálculos actuales se han realizado utilizando el paquete de simulación Viena ab initio (VASP) [28, 29], que se basa en la teoría funcional de la densidad, la base de onda plana y la representación de onda aumentada del proyector (PAW) [30]. El potencial de correlación de intercambio se trata dentro de la aproximación de gradiente generalizado (GGA) en forma de funcional Perdew-Burke-Ernzerhof (PBE) [31]. Para considerar las atracciones débiles entre capas en este cristal en capas, se han realizado cálculos de PBE-D2 [32] que incluyen la corrección semiempírica de van der Waals. Con el fin de obtener intervalos de banda más precisos, en este trabajo también se realizan los cálculos funcionales híbridos de Heyd-Scuseria-Ernzerhof (HSE06) [33,34,35,36]. Las funciones de onda de todos los sistemas calculados se expanden en ondas planas, con un corte de energía cinética de 500 eV. Las integraciones de la zona de Brillouin (BZ) se calculan utilizando un k especial -muestreo puntual del esquema Monkhorst-Pack [37], con un 45 × 45 × 1 Γ -rejilla centrada para el MoS monocapa y multicapa 2 y cuadrícula de 45 × 45 × 11 para el MoS 2 a granel para cálculos de PBE-D2. Para los cálculos de HSE06, un 9 × 9 × 1 Γ -rejilla centrada se utiliza para el MoS monocapa y multicapa 2 . Para el MoS monocapa y multicapa 2 , todos los cálculos son modelados por una supercélula con un espacio de vacío de 35 Å en la Z -dirección para evitar las interacciones entre MoS 2 adyacentes losas. Todas las configuraciones atómicas están completamente relajadas hasta que las fuerzas de Hellmann-Feynman en todos los átomos son menores que 0.01 eV / Å. Nuestros cálculos con polarización de espín muestran que las estructuras de bandas de MoS 2 las multicapas son bastante insensibles al efecto de polarización de espín (consulte el archivo adicional 1:Figura S1); por lo tanto, todos los resultados de los cálculos presentados se basan en el esquema de polarización sin espín.
Efectos excitónicos en monocapa MoS 2 resultan significativos y se han observado mediante fotoluminiscencia. Hemos empleado la cuasi-partícula G 0 W 0 método [38], y la ecuación de Bethe-Salpeter (BSE) [39, 40] para explicar los efectos excitónicos. Los huecos de banda de la monocapa MoS 2 se calculan en 2,32 y 2,27 eV para k -mallas de puntos de 15 × 15 × 1 y 24 × 24 × 1 Γ -rejilla centrada, obtenida por G 0 W 0 con cálculos de SOC. Las partes imaginarias de la función dieléctrica se muestran en la Fig.1, calculadas a partir de G 0 W 0 y el G 0 W 0 + Métodos de EEB. Se encuentran dos picos de excitones a 1,84 y 1,99 eV, lo que concuerda bien con las observaciones experimentales [4, 41]. Aunque el G 0 W 0 + El esquema BSE podría describir mejor los efectos excitónicos, en este artículo, presentamos solo los resultados (sin picos excitónicos) bajo el funcional GGA-PBE.
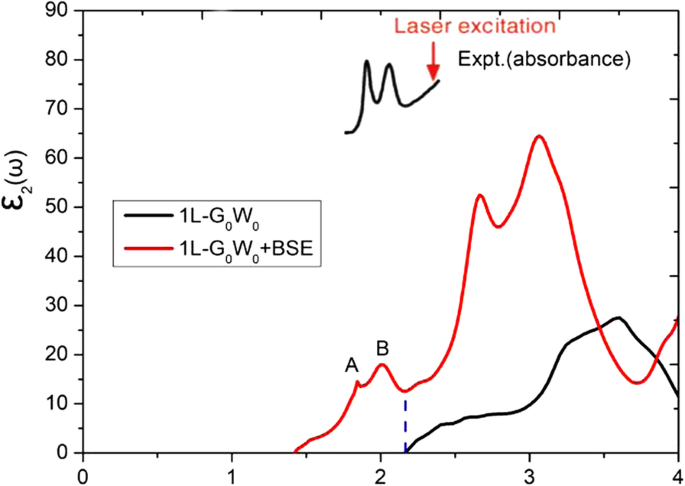
Las partes imaginarias de la función dieléctrica para monocapa MoS 2 , utilizando G 0 W 0 y G 0 W 0 + Métodos de EEB, respectivamente. El espectro de absorción experimental para MoS 2 se extrae de la Ref. [4]
Resultados y discusión
Estructuras electrónicas de MoS 2 Multicapas
MoS cristalino 2 ocurre naturalmente y tiene tres tipos cristalinos:1 T , 2 H y 3 R , que corresponde a cristales con celdas unitarias primitivas trigonales, hexagonales y romboédricas, respectivamente [9]. 2 H -MoS 2 se conoce como la estructura más estable [10]; por lo tanto, consideramos solo las 2 H tipo de MoS a granel 2 en este trabajo. Bulk 2 H -MoS 2 tiene una estructura de capas hexagonales que consta de capas de átomos de molibdeno rodeadas por seis átomos de azufre, con láminas de S-Mo-S apiladas de manera opuesta (mostrada en la Fig. 2). Las hojas vecinas a granel 2 H -MoS 2 están débilmente conectados con interacciones débiles de van der Waals. Una monocapa MoS 2 luego se puede exfoliar fácilmente a partir de la masa. Las constantes de celosía de MoS a granel 2 se calculan para ser a =b =3,19Å, c =12,41 Å, que son coherentes con los valores informados de a =b =3,18 Å, c =13,83 Å [18]. Las constantes de celosía optimizadas para monocapa MoS 2 son a =b =3,19 Å, que están de acuerdo con el MoS 2 a granel . Como se muestra en la Tabla 1, las constantes de celosía calculadas en a , b las direcciones son las mismas para diferentes números de capas de MoS 2 . También fue informado por Kumar et al. [19] que las constantes de celosía ( a, b ) de monocapa MoS 2 son casi idénticas a la mayoría.
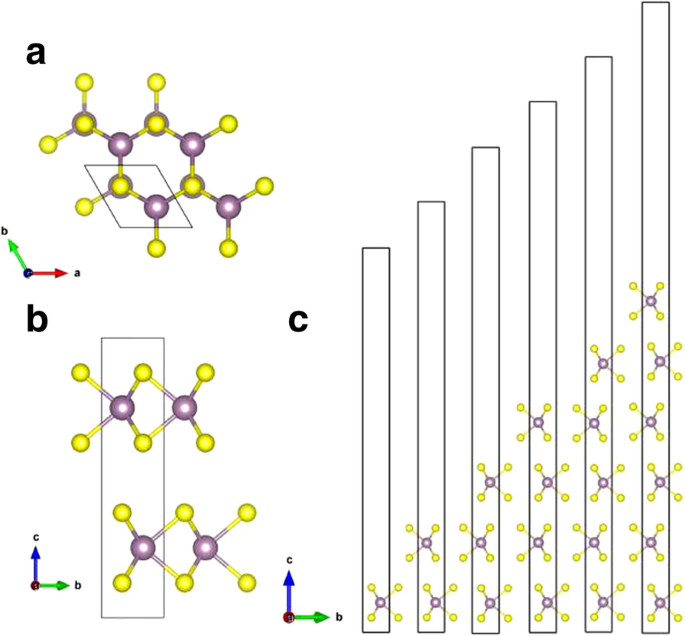
un Vista superior y b vista lateral de Bulk-MoS 2 . c Vista lateral de estructuras monocapa, bicapa, tricapa y de cuatro, cinco y seis capas de MoS 2 . Se muestra una celda unitaria en b . Las bolas púrpuras y amarillas representan átomos de Mo y S, respectivamente
La Figura 3 muestra las estructuras de bandas calculadas y la densidad electrónica de estados (DOS) de diferentes números de capas de MoS 2 . Resultados para MoS 2 monocapa, bicapa, tricapa y de cuatro capas, así como a granel se dan en la Fig.3, mientras que los resultados para MoS de cinco y seis capas 2 son muy similares a los de cuatro capas y a granel. Para monocapa MoS 2 , tanto el máximo de la banda de valencia (VBM) como el mínimo de la banda de conducción (CBM) aparecen en el punto K del BZ, exhibiendo una banda prohibida directa de 1,64 eV. Para MoS 2 bicapa y tricapa , tanto el VBM se ubica en el punto Γ mientras que el CBM se ubica en el punto K, lo que provoca brechas indirectas de 1,17 y 1,08 eV, respectivamente. Sin embargo, como el número de MoS 2 capas aumenta a cuatro y por encima de cuatro, todas las capas múltiples MoS 2 muestran los mismos caracteres que el VBM ubica en el punto Γ mientras que el CBM se encuentra entre los puntos Γ y K, que es el mismo que en el volumen. Los espacios de banda indirectos son 1.03 eV, 1.01 eV, 0.99 eV, 0.93 eV para MoS de cuatro, cinco, seis capas 2 y a granel, respectivamente. Tanto los cálculos PBE-D2 como HSE06 (Tabla 1) muestran que la banda prohibida fundamental aumenta monótonamente cuando el número de MoS 2 capas disminuye, lo que se debe a un gran confinamiento de electrones en la losa [4, 5, 19, 42]. Además, cuando el MoS 2 masivo la losa se reduce a una sola capa, se convierte en un semiconductor de banda prohibida directa, como se mencionó anteriormente, el MoS a granel 2 es un semiconductor de hueco indirecto. En la Fig. 3a, las estructuras de banda trazan el MoS 2 a granel mostrar división de bandas (en comparación con las de monocapa MoS 2 ), principalmente alrededor del  - punto, debido al acoplamiento entre capas [16]. Estructuras de bandas para dos capas (2L) y más de 2L MoS 2 exhiben una división similar de bandas debido nuevamente al acoplamiento entre capas. Sin embargo, la división de bandas a granel es algo más significativa que las de las multicapas MoS 2 , lo que indica un acoplamiento entre capas (ligeramente) más fuerte en el volumen que en las multicapas. Por otro lado, la división de bandas en la vecindad del punto K en BZ es muy pequeña. Los estados electrónicos en el punto K para la banda ocupada más alta se componen principalmente de d xy y \ ({d} _ {x ^ 2- {y} ^ 2} \) orbitales de átomos de Mo, así como pequeñas partes de ( p x , p y ) -orbitales de átomos de S (que se muestran en la Fig. 4b). Los átomos de Mo están situados en la capa media de la hoja S-Mo-S, lo que provoca un acoplamiento entre capas insignificante en el punto K (ya que los átomos más cercanos entre MoS 2 capas son S y S). Como se muestra en la Fig.4, se puede encontrar un acoplamiento entre capas más fuerte en el punto Γ en comparación con el del punto K, ya que los estados electrónicos en el punto Γ para la banda ocupada más alta están dominados por \ ({d} _ {z ^ 2} \ ) orbitales de átomos de Mo y p z orbitales de átomos de S. Por lo tanto, el acoplamiento S-S (acoplamiento entre capas) es claramente más fuerte en el punto Γ que en el punto K. Nuestros resultados son consistentes con otros trabajos teóricos [21]. En términos generales, la densidad electrónica de estados de MoS 2 de pocas capas son similares a los de MoS a granel 2 (ver Fig.3), ya que Bulk MoS 2 es en realidad un material en capas con interacciones débiles entre el MoS 2 capas.
- punto, debido al acoplamiento entre capas [16]. Estructuras de bandas para dos capas (2L) y más de 2L MoS 2 exhiben una división similar de bandas debido nuevamente al acoplamiento entre capas. Sin embargo, la división de bandas a granel es algo más significativa que las de las multicapas MoS 2 , lo que indica un acoplamiento entre capas (ligeramente) más fuerte en el volumen que en las multicapas. Por otro lado, la división de bandas en la vecindad del punto K en BZ es muy pequeña. Los estados electrónicos en el punto K para la banda ocupada más alta se componen principalmente de d xy y \ ({d} _ {x ^ 2- {y} ^ 2} \) orbitales de átomos de Mo, así como pequeñas partes de ( p x , p y ) -orbitales de átomos de S (que se muestran en la Fig. 4b). Los átomos de Mo están situados en la capa media de la hoja S-Mo-S, lo que provoca un acoplamiento entre capas insignificante en el punto K (ya que los átomos más cercanos entre MoS 2 capas son S y S). Como se muestra en la Fig.4, se puede encontrar un acoplamiento entre capas más fuerte en el punto Γ en comparación con el del punto K, ya que los estados electrónicos en el punto Γ para la banda ocupada más alta están dominados por \ ({d} _ {z ^ 2} \ ) orbitales de átomos de Mo y p z orbitales de átomos de S. Por lo tanto, el acoplamiento S-S (acoplamiento entre capas) es claramente más fuerte en el punto Γ que en el punto K. Nuestros resultados son consistentes con otros trabajos teóricos [21]. En términos generales, la densidad electrónica de estados de MoS 2 de pocas capas son similares a los de MoS a granel 2 (ver Fig.3), ya que Bulk MoS 2 es en realidad un material en capas con interacciones débiles entre el MoS 2 capas.
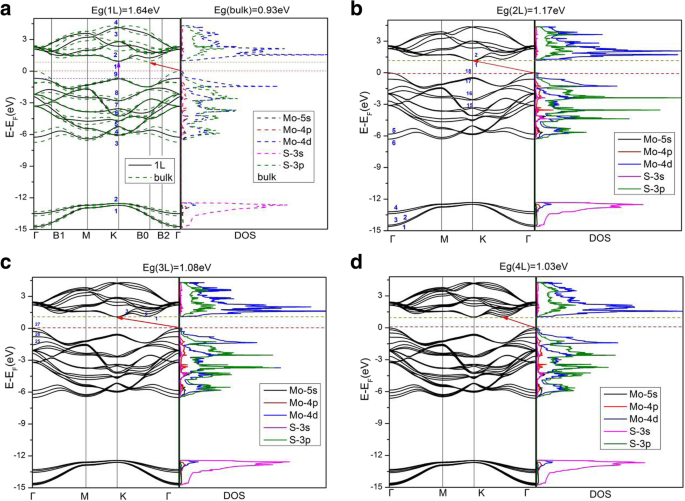
Estructuras de bandas calculadas y densidad de estados de a monocapa (líneas completas) y a granel (líneas discontinuas), b bicapa, c tricapa y d MoS 2 de cuatro capas . En a , las bandas ocupadas más altas para volumen y monocapa en el punto K se establecen en la misma energía. La banda de conducción mínima de volumen está en el punto B0
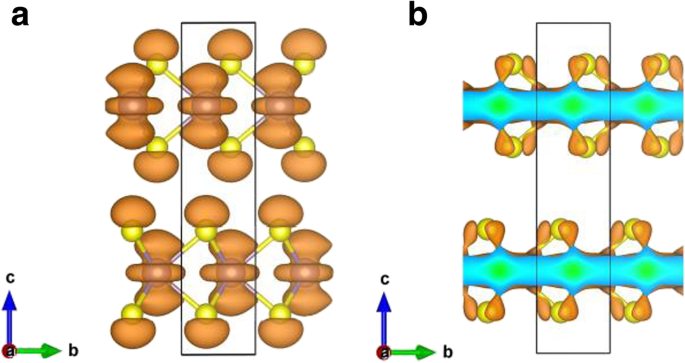
Las distribuciones de cargo de la banda ocupada más alta en a punto  y b punto K para MoS a granel 2 . El valor de isosuperficie se establece en 0,004 e / Å
3
y b punto K para MoS a granel 2 . El valor de isosuperficie se establece en 0,004 e / Å
3
Para explorar profundamente la naturaleza de unión en la monocapa MoS 2 , la densidad de carga de deformación se muestra en la Fig. 5a. La densidad de carga de deformación viene dada por Δρ 1 ( r ) = ρ ( r ) - ∑ μ ρ átomo ( r - R μ ) donde ρ ( r ) es la densidad de carga total y ∑ μ ρ átomo ( r - R u ) representa la superposición de densidades de carga atómica independientes. Los resultados demuestran que la unión en el MoS 2 La monocapa se caracteriza por una covalencia clara (líneas de contorno sólidas entre los átomos de Mo-S), así como interacciones iónicas fuertes (representadas por áreas alternas de contornos discontinuos y sólidos). Para ver la fuerza de unión en la monocapa MoS 2 en comparación con las de la masa, las diferencias de densidad de carga entre la monocapa y la MoS a granel 2 , Δρ 2 ( r ), también se presenta en la Fig. 5b. La diferencia de densidad de carga se define como Δρ 2 ( r ) = ρ 1 L ( r ) - ρ masivo ( r ), donde ρ 1 L ( r ) y ρ masivo ( r ) son las densidades de carga totales de MoS monocapa y a granel 2 , respectivamente. La Figura 5b indica una unión electrónica más fuerte en el caso de la monocapa que en el grueso, que se refleja en la acumulación de carga más grande (líneas de contorno sólidas) entre los átomos de Mo-S en la monocapa, así como por una unión iónica más fuerte en la monocapa MoS 2 dado que las áreas alternas de contornos discontinuos y sólidos en la Fig. 5b son más significativas que las del grueso. Además, la gráfica de diferencias de carga (Fig. 5b) indica que el átomo de Mo de la monocapa perdió más electrones que el átomo de Mo en la masa; por lo tanto, la ionicidad de la monocapa es más fuerte que la masa. Sin embargo, debe señalarse que el orden de magnitud de las diferencias de carga en la Fig. 5b son bastante pequeñas (el intervalo de contorno en la Fig. 5b es solo 2.5 × 10 −4 e / Å 3 ). A juzgar por el efecto de confinamiento cuántico, nuevamente, la interacción intracapa de la monocapa debería ser más fuerte que el volumen. Por lo tanto, se espera que la banda prohibida de la monocapa (1,64 eV) sea mayor que la masa (0,93 eV). El confinamiento cuántico disminuye con el aumento del número de capas [4, 42], lo que mejora el acoplamiento entre capas y reduce la interacción entre capas. Por lo tanto, la banda prohibida de MoS 2 disminuye con el aumento del acoplamiento entre capas. Las redistribuciones de densidad de carga entre capas para MoS 2 bicapa , Δρ 3 ( r ), también se presentan en la Fig. 5c. El Δρ 3 ( r ) viene dado por Δρ 3 ( r ) = ρ 2 L ( r ) - ρ capa1 ( r ) - ρ capa2 ( r ), donde ρ 2 L ( r ), ρ capa1 ( r ), ρ capa2 ( r ) son las densidades de carga de la bicapa MoS 2 , la primera capa de MoS bicapa 2 y la segunda capa de MoS bicapa 2 , respectivamente. Las densidades de carga de layer1 y layer2 de MoS bicapa 2 se calculan utilizando la estructura correspondiente en bicapa MoS 2 . Transferencia de carga desde MoS 2 capas (bicapa) a la región intermedia entre el MoS 2 Las capas se ven claramente en la Fig. 5c, mostradas como líneas de contorno continuas. Las interacciones iónicas entre capas atómicas en MoS 2 bicapa también son claros, como se ve en las áreas alternas de contornos discontinuos y sólidos. Nuevamente, el orden de magnitud de las densidades de carga entre capas, Δρ 3 ( r ), son muy pequeños (el intervalo de contorno es de solo 2,5 × 10 -4 e / Å 3 ). Generalmente, las redistribuciones de densidad de carga entre capas en 2L, 3L,…, MoS a granel 2 todos los sistemas son muy similares.
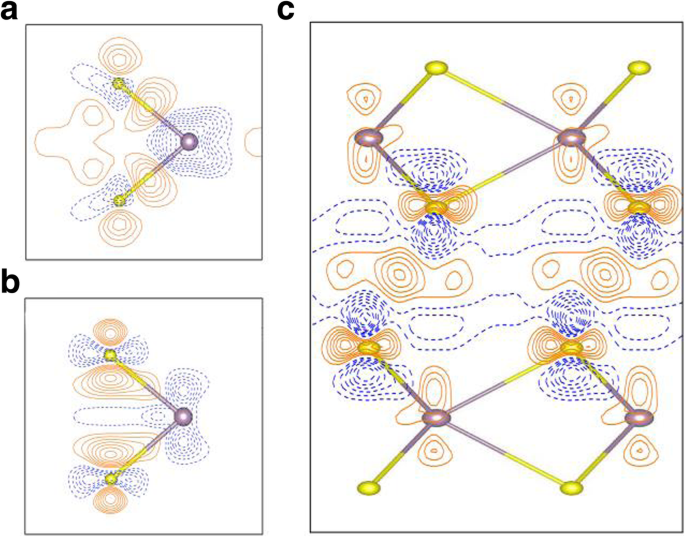
un Densidad de carga de deformación, Δ ρ 1 ( r ) = ρ ( r ) - ∑ μ ρ átomo ( r - R μ ), en la monocapa MoS 2 . b Diferencias entre las densidades de carga de la monocapa y la capa correspondiente de volumen. c La redistribución de la densidad de carga entre capas de MoS 2 bicapa . Intervalo de contorno de a es 2,5 × 10 −2 e / Å 3 , mientras que los de b y c son 2,5 × 10 −4 e / Å 3 . Las líneas de color naranja sólido y azul discontinuo corresponden a Δ ρ > 0 y Δ ρ <0 , respectivamente
Propiedades ópticas de MoS 2 Multicapas
Una vez que se obtienen las estructuras electrónicas del estado fundamental de un material, se pueden investigar las propiedades ópticas. La parte imaginaria de la función dieléctrica \ ({\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) \) está determinada por la siguiente ecuación [43]:
$$ {\ Displaystyle \ begin {array} {c} {\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) =\ frac {4 {\ pi} ^ 2 {e} ^ 2} {\ Omega} {\ lim} _ {q \ to 0} \ frac {1} {q ^ 2} \ underset {c, v, k} {\ Sigma} 2 {w} _k \ delta \ left ({E } _ {ck} - {E} _ {vk} - \ mathrm {\ hslash} \ omega \ right) \\ {} \ times \ left \ langle {u} _ {ck + {e} _ {\ alpha} q } | {u} _ {vk} \ right \ rangle \ left \ langle {u} _ {ck + {e} _ {\ beta} q} | {u} _ {vk} \ right \ rangle \ ast \ end { matriz}} $$ (1)donde los índices α y β denotar direcciones cartesianas, c y v se refieren a las bandas de conducción y valencia, E ck y E vk son las energías de las bandas de conducción y de valencia, respectivamente. La inversión de Kramers-Kronig se puede aplicar para adquirir la parte real de la función dieléctrica \ ({\ varepsilon} _1 ^ {\ alpha \ beta} \ left (\ omega \ right) \) determinada por la parte imaginaria \ ({\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) \):
$$ {\ varepsilon} _1 ^ {\ alpha \ beta} \ left (\ omega \ right) =1 + \ frac {2} {\ pi} P {\ int} _0 ^ {\ infty} \ frac {\ varepsilon_2 ^ {\ alpha \ beta} \ left (\ omega \ hbox {'} \ right) \ omega \ hbox {'}} {\ omega {\ hbox {'}} ^ 2 - {\ omega} ^ 2 + i \ eta} d \ omega \ hbox {'} $$ (2)en el que P representa el valor principal. Desde MoS 2 tiene una estructura uniaxial, ε xx ( ω ) es entonces idéntico a ε yy ( ω ). En este trabajo, solo necesitamos discutir el vector eléctrico E que es paralelo al x-y avión, es decir, E || x es paralelo al MoS 2 x-y avión.
Para investigar espectros ópticos detallados de MoS 2 sistema, el coeficiente de absorción α ( ω ) y la reflectividad R ( ω ) fueron calculados por la parte real ε 1 ( ω ) y la parte imaginaria 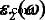 de la función dieléctrica. Las ecuaciones de los parámetros mencionados se presentan a continuación:
de la función dieléctrica. Las ecuaciones de los parámetros mencionados se presentan a continuación:
Si el elemento de matriz \ (\ left \ langle {u} _ {ck + {e} _ {\ alpha} q} | {u} _ {vk} \ right \ rangle \) varía muy lentamente a medida que k -vector, el término \ (\ left \ langle {u} _ {ck + {e} _ {\ alpha} q} | {u} _ {vk} \ right \ rangle \ left \ langle {u} _ {ck + { e} _ {\ beta} q} | {u} _ {vk} \ right \ rangle \ ast \) en la ecuación. (1) puede tomarse fuera del total. En Eq. (1), la mayor parte de la dispersión en \ ({\ varepsilon} _2 ^ {\ alpha \ beta} \ left (\ omega \ right) \) se debe a la suma sobre la función delta δ ( E ck - E vk - ℏ ω ). Esta suma se puede transformar en una integración sobre la energía definiendo una densidad conjunta de estados (JDOS) [25, 44],
$$ {J} _ {cv} \ left (\ omega \ right) =\ frac {1} {4 {\ pi} ^ 3} \ int \ frac {dS_k} {\ nabla_k \ left ({E} _ { ck} - {E} _ {vk} \ right)} $$ (5)en el que ℏ ω es igual a E ck - E vk , S k representa la superficie de energía constante denotada por E ck - E vk =ℏ ω =Const. La densidad conjunta de estados J cv ( ω ) está asociado con las transiciones de las bandas de valencia a las bandas de conducción, y los picos grandes en J cv ( ω ) se originará en el espectro donde ∇ k ( E ck - E vk ) ≈ 0. Puntos en k -espacio donde ∇ k ( E ck - E vk ) =0 se denominan puntos críticos o singularidades de van Hove (VHS), y E ck - E vk se denominan energías de punto crítico [26, 27]. Los puntos críticos ∇ k E ck =∇ k E vk =0 generalmente ocurre solo en puntos de alta simetría, mientras que los puntos críticos ∇ k E ck =∇ k E vk ≠ 0 puede ocurrir en cualquier punto general de la zona de Brillouin [27, 45]. En el caso bidimensional, hay tres tipos de puntos críticos, es decir, P 0 (punto mínimo), P 1 (punto de silla) y P 2 (punto máximo). En los puntos P 0 o P 2 , se produjo una singularidad de función escalonada en JDOS, mientras que en el punto de silla P 1 , JDOS fue descrito por una singularidad logarítmica [27]. Más detalladamente, el E c ( k x , k y ) - E v ( k x , k y ) se puede ampliar en una serie de Taylor sobre el punto crítico. Limitando la expansión a términos cuadráticos, con el término lineal no ocurre debido a la propiedad de la singularidad, entonces tenemos
$$ {E} _c \ left ({k} _x, {k} _y \ right) - {E} _v \ left ({k} _x, {k} _y \ right) ={E} _0 + \ frac {\ mathrm {\ hslash}} {2} \ left ({b} _x \ frac {k_x ^ 2} {m_x} + {b} _y \ frac {k_y ^ 2} {m_y} \ right) $$ (6)Por tanto, surgen tres tipos de puntos críticos. Para P 0 , ( b x > 0, b y > 0), para P 1 , ( b x > 0, b y <0) o ( b x <0, b y > 0) y para P 2 , ( b x <0, b y <0). En este artículo, para el caso de MoS 2 multicapas, solo la P 0 se trata de un punto crítico.
La Figura 6a muestra las partes imaginarias de la función dieléctrica, \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \), de MoS 2 multicapas para E || x. Encontramos un fenómeno interesante de que las partes imaginarias de la función dieléctrica \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) poseen mesetas, y las mesetas de diferentes capas de MoS 2 son casi iguales en el rango de 1,75 eV ~ 2,19 eV. Desde el umbral de energía hasta 1,75 eV, \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) son bastante diferentes para diferentes multicapas de MoS 2 . Las energías umbral y final de las mesetas en diferentes capas son diferentes, especialmente, el rango de energía de la meseta \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) de la monocapa es significativamente más amplia que las de otras multicapas. El umbral de energía de la monocapa MoS 2 La función dieléctrica es igual a su banda prohibida directa de 1,64 eV. Sin embargo, el umbral de energía de la función dieléctrica bicapa no es el intervalo de banda indirecto de 1,17 eV, sino el intervalo mínimo de energía directa de 1,62 eV entre las bandas de valencia y conducción. Esto se debe a que estudiamos solo las transiciones entre las bandas de valencia y conducción con el mismo vector de onda de electrones, que se clasifican como transiciones ópticas directas [36, 47]. Como el número de MoS 2 capas aumentadas a 4, encontramos que \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) de MoS multicapa 2 los sistemas eran casi indistinguibles del volumen. Por lo tanto, discutimos aquí en detalle solo las mesetas de la monocapa, bicapa y tricapa, así como MoS a granel 2 . Las mesetas \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) de monocapa, bicapa, tricapa y MoS a granel 2 terminó en 2,57 eV, 2,28 eV, 2,21 eV y 2,19 eV, respectivamente. Para explicar esto con más precisión, JDOS de monocapa, bicapa, tricapa y MoS a granel 2 se muestran en la Fig. 7. De la Fig. 7, las mesetas también se muestran en el JDOS. Las mesetas de JDOS monocapa, bicapa y tricapa terminaron en 2.57 eV, 2.28 eV, 2.21 eV, respectivamente, que son exactamente iguales a las de su \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right ) \). Para MoS a granel 2 , la meseta de JDOS terminó en 2,09 eV, que es ligeramente menor que 2,19 eV en la función dieléctrica \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \).
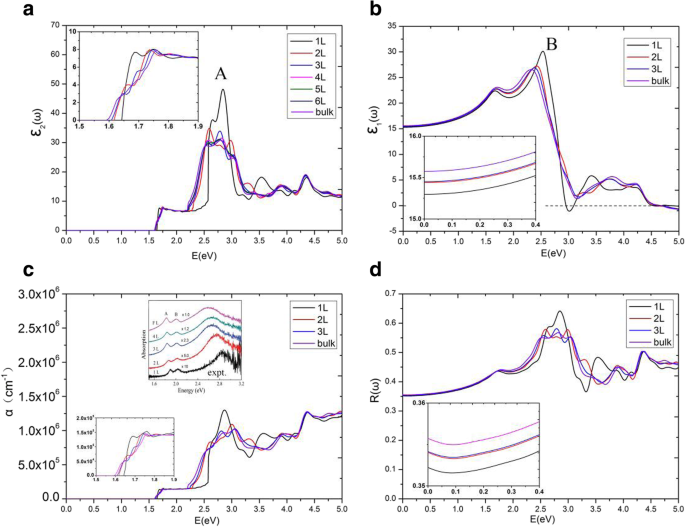
un Las partes imaginarias de la función dieléctrica, b las partes reales de la función dieléctrica, c los coeficientes de absorción, y d los espectros de reflectividad, para diferentes números de MoS 2 capas. El recuadro en c también muestra los datos experimentales [46]
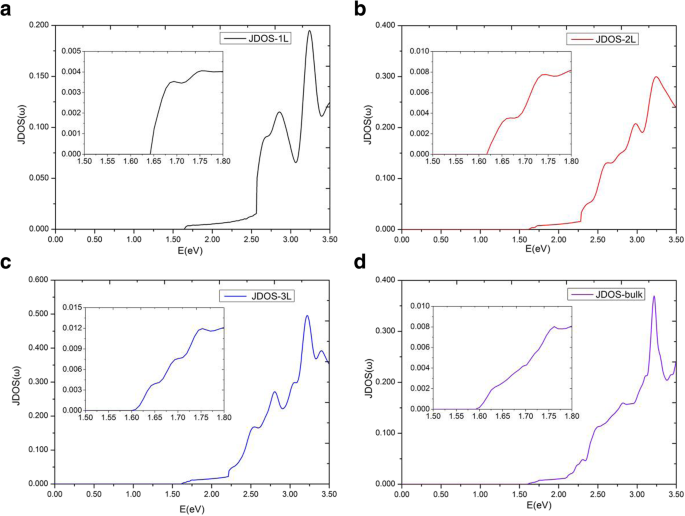
Densidad conjunta de estados para el MoS monocapa, bicapa, tricapa y a granel 2
Para analizar con precisión las transiciones electrónicas y para un análisis detallado de la función dieléctrica \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \), las brechas de energía directa, ΔE (NC - NV), entre bandas de conducción y valencia de monocapa, bicapa, tricapa y MoS a granel 2 se presentan en la Fig. 8. Las notaciones NC y NV representan los números ordinales de las bandas de conducción y valencia. Por lo tanto, NC =1, 2 y 3 significan la banda de material más baja, la segunda más baja y la tercera más baja desocupada. Por otro lado, NV =9, 18 y 27 (que depende del número de electrones en la celda unitaria) significan la banda ocupada más alta de monocapa, bicapa y tricapa MoS 2 , respectivamente. Para monocapa, en la región de 0 ~ 2.57 eV, las transiciones electrónicas se encuentran contribuidas solo desde la banda ocupada más alta NV =9 a la banda desocupada más baja NC =1. De la Fig. 8a, aparece un mínimo en el punto de simetría alta K y el umbral de JDOS (Fig. 7a) aparece en 1,64 eV, que en realidad es la banda prohibida directa de la monocapa MoS 2 . En la vecindad del punto de alta simetría K, la curva de ΔE (NC =1 - NV =9) es similar a una parábola para la monocapa MoS 2 . Por lo tanto, ∇ k ( E ck - E vk ) =0 en el punto K, lo que significa un punto crítico en el punto de alta simetría K. En una estructura bidimensional, este punto crítico pertenece a P 0 singularidad de tipo [27], y por lo tanto conduce a un paso en el JDOS. Por lo tanto, la energía umbral de la meseta JDOS se encuentra en la energía del punto crítico 1,64 eV. La energía final de la meseta JDOS está cerca de 2.57 eV, que es el resultado de la aparición de dos P 0 escriba singularidades en el punto B1 ( k =(0.00, 0.16, 0.00)) y el punto B2 ( k =(- 0,10, 0,20, 0,00)). Las pendientes de la curva ΔE (NC =1 - NV =9) cerca de los dos puntos críticos B1 y B2 son muy pequeñas, lo que da lugar a un rápido aumento de JDOS (ver Ec. (5)). Los principales puntos críticos para estas largas mesetas de JDOS se enumeran en la Tabla 2, incluido el tipo, la ubicación, las bandas de transición y la brecha de energía directa ΔE (NC - NV). Además, encontramos que ∇ k E ck =∇ k E vk =0 ocurrió en el punto de alta simetría K donde las pendientes de las bandas de valencia y conducción son horizontales. Mientras que ∇ k E ck =∇ k E vk ≠ 0 ocurrió en los puntos B1 y B2, lo que significa que las pendientes de dos bandas son paralelas. Simultáneamente, el análisis de las estructuras de bandas y las brechas de energía directa (ver Fig. 8a) para la monocapa muestra que, cuando la brecha de energía directa ΔE está por debajo de 2.65 eV, solo las transiciones entre NV =9 y NC =1 contribuyen a JDOS; cuando el ΔE es mayor que 2.65 eV, las transiciones de NV =9 a NC =2 también comienzan a contribuir a JDOS; mientras que cuando el ΔE alcanza más de 2.86 eV, las transiciones NV =9 a NC =3 tienen efecto en JDOS. Cabe señalar que para energía superior a 2,65 eV, muchas bandas en la Fig. 8a contribuirán a JDOS. JDOS de monocapa MoS 2 exhibe una meseta en el rango de 1,64 ~ 2,57 eV y la variación de la expresión | M vc | 2 / ω 2 se encuentra pequeño en este rango. Según las Ecs. (1) y (5), la parte imaginaria de la función dieléctrica \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) se decide principalmente por el JDOS y los elementos de la matriz de transición, esto da una meseta similar para la parte imaginaria de la función dieléctrica \ ({\ varepsilon} _2 ^ {xx} \ left (\ omega \ right) \) en comparación con JDOS.
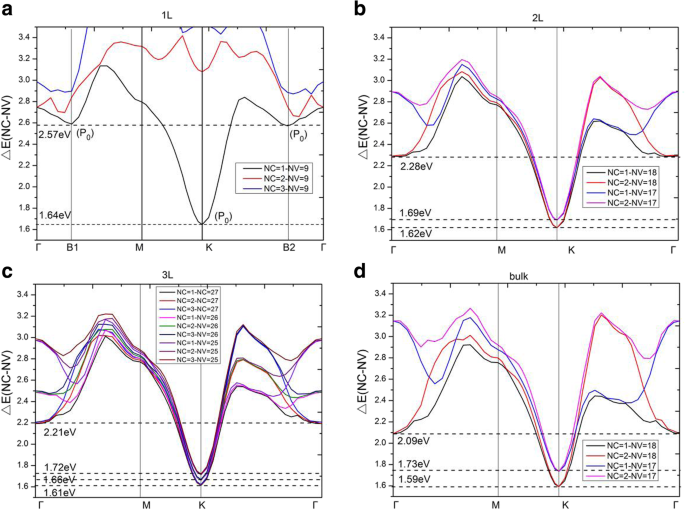
Direct energy gaps, ΔE(NC − NV), between conduction and valence bands for the a monolayer, b bilayer, c trilayer, and d bulk MoS2 . un - d There are three, six, twelve, and six critical points in interband transitions for the monolayer, bilayer, trilayer, and bulk MoS2 , respectivamente
For bilayer MoS2 , in the region of 0 ~ 2.28 eV (the endpoint of JDOS plateau), the electronic transitions are contributed to NV =17, 18 to NC =1, 2. The minimum energy in ΔE(NC − NV) is situated at the K point with a gap of 1.62 eV. In Fig. 8b, similar to monolayer MoS2 , bilayer MoS2 holds two parabolic curves going upward (which come from ΔE(NC = 1 − NV = 18) and ΔE(NC = 2 − NV = 18)) at K point. Therefore, there are two P 0 type singularities (∇k ( E ck - E vk ) = 0) at K point, causing a step in the JDOS. The critical point energies are both 1.62 eV, this is because that the conduction bands (NC =1 and NC =2) are degenerate at point K (as shown in Fig. 3b), which results in the same direct energy gap between transitions of NV =18 to NC =1 and NV =18 to NC =2. From Fig. 8b, as the direct energy gap is increased to 1.69 eV, two new parabolas (which come from ΔE(NC = 1 − NV = 17) and ΔE(NC = 2 − NV = 17)) appear and two new singularities emerge again at K point in the direct energy gap graph, leading to a new step in JDOS for bilayer MoS2 (see Fig. 7b). As a result, the JDOS of the bilayer MoS2 has two steps around the threshold of long plateau (see inset in Fig. 7b). Two parabolas (in Fig. 8b) contribute to the first step and four parabolas contribute to the second step in JDOS. It means that the value of the second step is roughly the double of the first one. As the ΔE reaches to 2.28eV, two new singularities appear at Γ point (where interband transitions come from Γ(NV =18→NC =1) and Γ(NV =18→NC =2)), which have great contribution to the JDOS and bring the end to the plateau. Our calculations demonstrate that ∇k E ck = ∇k E vk = 0 are satisfied not only at high symmetry point K, but also at high symmetry point Γ. Similar to the case of monolayer, we found that the term of |Mvc | 2 / ω 2 is a slowly varying function in the energy range of bilayer JDOS plateau; hence, \( {\varepsilon}_2^{xx}\left(\omega \right) \) of bilayer have a similar plateau in the energy range.
For trilayer MoS2 , in the region of 0 ~ 2.21 eV, the JDOS are contributed from electronic transitions of NV =25, 26, and 27 to NC =1, 2, and 3. As shown in Fig. 8c, trilayer MoS2 have nine singularities at three different energies (ΔE =1.61 eV, 1.66 eV, and 1.72 eV, respectively) at the K point. Figure 3c depicts that the conduction bands (NC =1, 2, 3) are three-hold degenerate at point K; this means that there are three singularities at each critical point energy. According to our previous analysis, the JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) of trilayer MoS2 will show three steps near the thresholds of the long plateaus, the endpoints of the long plateaus of trilayer JDOS, and \( {\varepsilon}_2^{xx}\left(\omega \right) \) are then owing to the appearance of three singularities at Γ point with ΔE =2.21 eV (see Fig. 7c), which come from the interband transitions of Γ(NV =27→NC =1, 2, 3).
For bulk MoS2 , the thresholds of \( {\varepsilon}_2^{xx}\left(\omega \right) \) and JDOS are also located at K point, with the smallest ΔE(NC − NV) equals to 1.59 eV. Nevertheless, there is no obvious step appeared in the thresholds of plateaus for both the \( {\varepsilon}_2^{xx}\left(\omega \right) \) and JDOS (see Fig. 6a and Fig. 7d). Based on the previous analysis, the number of steps in the monolayer, bilayer, and trilayer MoS2 are 1, 2, and 3, respectively. As the number of MoS2 layers increases, the number of steps also increases in the vicinity of the threshold energy. Thus, in the bulk MoS2 , the JDOS curve is composed of numerous small steps around the threshold energy of the long plateau, and finally the small steps disappear near the threshold energy since the width of the small steps decreases. In the region of 0 ~ 2.09 eV, the electron transitions of bulk MoS2 are contributed to NV =17, 18 to NC =1, 2. The 2.09 eV is the endpoint of JDOS plateau of bulk MoS2 , which is attributed to two singularities, i.e., the interband transitions of Γ(NV =18→NC =1) as well as Γ(NV =18→NC =2), as presented in Fig. 8d. However, the plateau endpoint of the imaginary part of dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) is 2.19 eV, which is greater than the counterpart of JDOS (e.g., 2.09 eV). Checked the transition matrix elements, it verified that some transitions are forbidden by the selection rule in the range of 2.09 eV to 2.19 eV. Therefore, the imaginary part of the dielectric function \( {\varepsilon}_2^{xx}\left(\omega \right) \) is nearly invariable in the range of 2.09 ~ 2.19 eV. As a result, the plateau of \( {\varepsilon}_2^{xx}\left(\omega \right) \) of bulk MoS2 is then 1.59 ~ 2.19 eV.
It has been shown that these thresholds of the JDOS plateaus are determined by singularities at the K point for all of the studied materials, see Fig. 8. The endpoint energy of the monolayer JDOS plateau is determined by two critical points at B1 and B2 (Fig. 8a). Nevertheless, the endpoint energies of bilayer, trilayer, and bulk JDOS plateaus are all dependent on the critical points at Γ(Fig. 8b–d). The interlayer coupling near point Γ is significantly larger than the near point K for all the systems of multilayer MoS2 . The smallest direct energy gap decreases and the interlayer coupling increases as the number of layers grow. With the layer number increases, a very small decrease of direct energy gap at point K and a more significant decrease of direct energy gap at point Γ can be observed, as a result, a faint red shift in the threshold energy and a bright red shift in the end of both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus can also be found. For monolayer MoS2 , the smallest ΔE(NC − NV) at point Γ is 2.75 eV which is larger than that at point B1 (or point B2) with a value around 2.57 eV. When it goes to multilayer and bulk MoS2 , the strong interlayer coupling near point Γ makes the smallest ΔE(NC − NV) at Γ less than those at point B1 (or point B2). Hence, monolayer owns the longest plateau of JDOS, which is between 1.64 eV and 2.57 eV. The shortest plateau of JDOS (from 1.59 eV to 2.09 eV) is shown in the bulk.
As the energy is increased to the value larger than the endpoint of long platform of the dielectric function, a peak A can be found at the position around 2.8 eV, for almost all the studied materials (Fig. 6a). The width of peak A for monolayer is narrower compared with those of multilayer MoS2; however, the intensity of peak A for monolayer is found to be a little stronger than multilayers. The differences between the imaginary parts of dielectric function for the monolayer and multilayer MoS2 are evident, on the other hand, the differences are small for multilayer MoS2 .
In order to explore the detailed optical spectra of MoS2 multilayers, the real parts of the dielectric function ε 1 ( ω ), the absorption coefficients α ( ω ), and the reflectivity spectra R ( ω ) are presented in Fig. 6b–d. Our calculated data of bulk MoS2 for the real and imaginary parts of the dielectric function, ε 1 ( ω ) y ε 2 ( ω ), the absorption coefficient α ( ω ) and the reflectivity R ( ω ) agree well with the experimental data, except for the excitonic features near the band edge [48,49,50]. The calculated values of 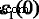 , which is called the static dielectric constant, for MoS2 multilayers and bulk can be found in Table 1. From Table 1, the calculated values of \( {\varepsilon}_1^{xx}(0) \) for multilayers and bulk MoS2 are all around 15.5, which is very close to the experimental value of 15.0 for bulk MoS2 [50]. The values of \( {\varepsilon}_1^{xx}(0) \) increase with the increasing number of MoS2 capas. For monolayer MoS2 , a clear peak B of \( {\varepsilon}_1^{xx}\left(\omega \right) \) appears about 2.54 eV. Peak B of monolayer is clearly more significant than multilayers, and they are all similar for multilayer MoS2 . As the layer number increases, the sharp structures (peak B) also move left slightly. In Fig. 6c, we also observe the emergence of long plateaus in the absorption coefficients, and absorption coefficients are around 1.5 × 10
5
cm
−1
at the long plateaus. There are also small steps around the thresholds for the absorption coefficients, which are consistent to those of the imaginary parts of dielectric function. With the layer number increases, the threshold energy of absorption coefficient decreases, while the number of small steps increases at the starting point of the plateau. For monolayer and multilayer MoS2 , strong absorption peaks emerge at visible light range (1.65–3.26 eV), and the monolayer MoS2 own a highest absorption coefficient of 1.3 × 10
6
cm
−1
. The theoretical absorption coefficients for different number of MoS2 layers are compared with confocal absorption spectral imaging of MoS2 (the inset) [46], as shown in Fig. 6c. For monolayer and multilayer MoS2 , a large peak of α ( ω ) can be found at the position around 2.8 eV for both the calculation and experiment [46, 51]. Furthermore, a smoothly increase of α ( ω ) can be found between 2.2 and 2.8 eV for both the theoretical and experimental curves. Therefore, from Fig. 6c, the calculated absorption coefficients of MoS2 multilayers show fairly good agreement with the experimental data [46], except for the excitonic peaks. The reflectivity spectra are given in Fig. 6d. The reflectivity spectra of MoS2 multilayers are all about 0.35–0.36 when energy is zero, which means that MoS2 system can reflect about 35 to 36% of the incident light. In the region of visible light, the maximum reflectivity of monolayer MoS2 is 64%, while the maxima of multilayer and bulk MoS2 are all about 58%. Because of the behaviors discussed, MoS2 monolayer and multilayers are being considered for photovoltaic applications.
, which is called the static dielectric constant, for MoS2 multilayers and bulk can be found in Table 1. From Table 1, the calculated values of \( {\varepsilon}_1^{xx}(0) \) for multilayers and bulk MoS2 are all around 15.5, which is very close to the experimental value of 15.0 for bulk MoS2 [50]. The values of \( {\varepsilon}_1^{xx}(0) \) increase with the increasing number of MoS2 capas. For monolayer MoS2 , a clear peak B of \( {\varepsilon}_1^{xx}\left(\omega \right) \) appears about 2.54 eV. Peak B of monolayer is clearly more significant than multilayers, and they are all similar for multilayer MoS2 . As the layer number increases, the sharp structures (peak B) also move left slightly. In Fig. 6c, we also observe the emergence of long plateaus in the absorption coefficients, and absorption coefficients are around 1.5 × 10
5
cm
−1
at the long plateaus. There are also small steps around the thresholds for the absorption coefficients, which are consistent to those of the imaginary parts of dielectric function. With the layer number increases, the threshold energy of absorption coefficient decreases, while the number of small steps increases at the starting point of the plateau. For monolayer and multilayer MoS2 , strong absorption peaks emerge at visible light range (1.65–3.26 eV), and the monolayer MoS2 own a highest absorption coefficient of 1.3 × 10
6
cm
−1
. The theoretical absorption coefficients for different number of MoS2 layers are compared with confocal absorption spectral imaging of MoS2 (the inset) [46], as shown in Fig. 6c. For monolayer and multilayer MoS2 , a large peak of α ( ω ) can be found at the position around 2.8 eV for both the calculation and experiment [46, 51]. Furthermore, a smoothly increase of α ( ω ) can be found between 2.2 and 2.8 eV for both the theoretical and experimental curves. Therefore, from Fig. 6c, the calculated absorption coefficients of MoS2 multilayers show fairly good agreement with the experimental data [46], except for the excitonic peaks. The reflectivity spectra are given in Fig. 6d. The reflectivity spectra of MoS2 multilayers are all about 0.35–0.36 when energy is zero, which means that MoS2 system can reflect about 35 to 36% of the incident light. In the region of visible light, the maximum reflectivity of monolayer MoS2 is 64%, while the maxima of multilayer and bulk MoS2 are all about 58%. Because of the behaviors discussed, MoS2 monolayer and multilayers are being considered for photovoltaic applications.
Conclusiones
In this study, by employing ab initio calculations, the electronic and optical properties of MoS2 multilayers are investigated. Compared to bulk MoS2 , the covalency and ionicity of monolayer MoS2 are found to be stronger, which results from larger quantum confinement in the monolayer. With the increase of the layer number, quantum confinement and intra-layer interaction both decrease, meanwhile, the interlayer coupling increases, which result in the decrease of the band gap and the minimum direct energy gap. As the layer number becomes larger than two, the optical and electronic properties of MoS2 multilayers start to exhibit those of bulk. Band structures of multilayers and bulk show splitting of bands mainly around the Γ-point; however, splitting of bands in the vicinity of K point are tiny, owing to the small interlayer coupling at point K.
For optical properties, Van Hove singularities lead to the occurrence of long plateaus in both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \). At the beginnings of these long plateaus, monolayer, bilayer, and trilayer structures appear one, two, and three small steps, respectively. With the layer number increases, the number of small steps increases and the width of the small steps decreases, leading to unobvious steps. A small red shift in the threshold energy and a noticeable red shift in the end of both JDOS and \( {\varepsilon}_2^{xx}\left(\omega \right) \) plateaus are observed, since the increased number of layers leads to small changes in the direct energy gap near point K (weak interlayer coupling) and larger changes near point Γ (stronger interlayer coupling). Thus, the longest plateau and shortest plateau of JDOS are from the monolayer and bulk, respectively. Our results demonstrate that the differences between electronic and optical properties for monolayer and multilayer MoS2 are significant; however, the differences are not obvious between the multilayer MoS2 . The present data can help understand the properties of different layers of MoS2 , which should be important for developing optoelectronic devices.
Disponibilidad de datos y materiales
Los conjuntos de datos que respaldan las conclusiones de este artículo se incluyen dentro del artículo.
Abreviaturas
- Δ E:
-
The direct energy gap
- 1L:
-
Monolayer MoS2
- 2L:
-
Bilayer MoS2
- 3L:
-
Trilayer MoS2
- 4L:
-
Four-layer MoS2
- 5L:
-
Five-layer MoS2
- 6L:
-
Six-layer MoS2
- BSE:
-
Bethe-Salpeter equation
- BZ:
-
Brillouin zone
- CBM:
-
Banda de conducción mínima
- GGA:
-
Aproximación de gradiente generalizada
- GW:
-
Quasi-particle energy calculation
- JDOS:
-
Joint density of states
- MoS 2 :
-
Disulfuro de molibdeno
- NC:
-
The ordinal numbers of conduction band
- NV:
-
The ordinal numbers of valence band
- PAW:
-
Projector augmented wave
- PBE:
-
Perdew-Burke-Ernzerhof
- VASP:
-
Paquete de simulación Viena ab initio
- VBM:
-
Máximo de banda de valencia
- VHS:
-
Van Hove singularity
Nanomateriales
- Presentación de la estructura atómica y electrónica de las nanofibras de carbono de copa apilada
- Estructura y propiedades electrónicas de la nanoarcilla de caolinita dopada con metal de transición
- Modulación de las propiedades de anisotropía óptica y electrónica de ML-GaS por campo eléctrico vertical
- Síntesis fácil y propiedades ópticas de nanocristales y nanovarillas de selenio pequeños
- Efectos del espesor de la bicapa en las propiedades morfológicas, ópticas y eléctricas de los nanolaminados de Al2O3 / ZnO
- Propiedades ópticas y electrónicas de fotodiodos N + / P de silicio hiperdopado con azufre inducido por láser de femtosegundo
- Prueba de las propiedades estructurales, electrónicas y magnéticas de Ag n V (n =1–12) Clusters
- Dependencia de la toxicidad de las nanopartículas en sus propiedades físicas y químicas
- Propiedades ópticas de películas de ZnO dopado con Al en la región infrarroja y sus aplicaciones de absorción
- Monocapa de g-GaN adsorbido por metales alcalinos:funciones de trabajo ultrabajo y propiedades ópticas
- Propiedades electrónicas de la adsorción de átomos de vanadio en una superficie limpia y cubierta de grafeno de Cu (111)



