MATLAB - Transformaciones

MATLAB proporciona comandos para trabajar con transformadas, como las transformadas de Laplace y Fourier. Las transformaciones se utilizan en ciencia e ingeniería como una herramienta para simplificar el análisis y ver los datos desde otro ángulo.

Por ejemplo, la transformada de Fourier nos permite convertir una señal representada en función del tiempo a una función de frecuencia. La transformada de Laplace nos permite convertir una ecuación diferencial en una ecuación algebraica.

MATLAB proporciona el laplace , fourier y fft comandos para trabajar con transformadas de Laplace, Fourier y Fast Fourier.

La transformada de Laplace

La transformada de Laplace de una función del tiempo f(t) viene dada por la siguiente integral −

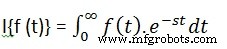
La transformada de Laplace también se denota como transformada de f(t) a F(s). Puede ver que este proceso de transformación o integración convierte f(t), una función de la variable simbólica t, en otra función F(s), con otra variable s.

La transformada de Laplace convierte las ecuaciones diferenciales en ecuaciones algebraicas. Para calcular una transformada de Laplace de una función f(t), escriba −

laplace(f(t))

Ejemplo

En este ejemplo, calcularemos la transformada de Laplace de algunas funciones de uso común.

Cree un archivo de script y escriba el siguiente código −

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Cuando ejecuta el archivo, muestra el siguiente resultado −

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

La transformada inversa de Laplace

MATLAB nos permite calcular la transformada inversa de Laplace usando el comando ilaplace .

Por ejemplo,

ilaplace(1/s^3)

MATLAB ejecutará la instrucción anterior y mostrará el resultado −

ans =
   t^2/2

Ejemplo

Cree un archivo de script y escriba el siguiente código −

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Cuando ejecuta el archivo, muestra el siguiente resultado −

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

Las transformadas de Fourier

La transformada de Fourier comúnmente transforma una función matemática del tiempo, f(t), en una nueva función, a veces denotada por o F, cuyo argumento es la frecuencia con unidades de ciclos/s (hertz) o radianes por segundo. La nueva función se conoce entonces como la transformada de Fourier y/o el espectro de frecuencias de la función f.

Ejemplo

Cree un archivo de script y escriba el siguiente código en él −

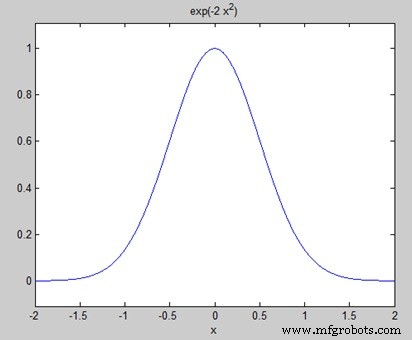
syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Cuando ejecuta el archivo, MATLAB traza el siguiente gráfico −

Se muestra el siguiente resultado −

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

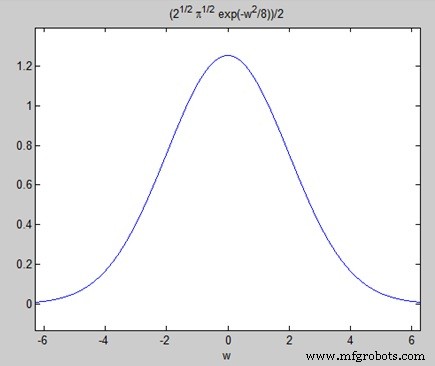
Trazar la transformada de Fourier como −

ezplot(FT)

Da el siguiente gráfico −

Transformadas inversas de Fourier

MATLAB proporciona el ifourier comando para calcular la transformada inversa de Fourier de una función. Por ejemplo,

f = ifourier(-2*exp(-abs(w)))

MATLAB ejecutará la instrucción anterior y mostrará el resultado −

f =
   -2/(pi*(x^2 + 1))