MATLAB-Gráficos

Este capítulo continuará explorando las capacidades de trazado y gráficos de MATLAB. Hablaremos −

• Dibujar gráficos de barras
• Dibujar contornos
• Gráficas tridimensionales

Dibujar gráficos de barras

La barra El comando dibuja un gráfico de barras bidimensional. Tomemos un ejemplo para demostrar la idea.

Ejemplo

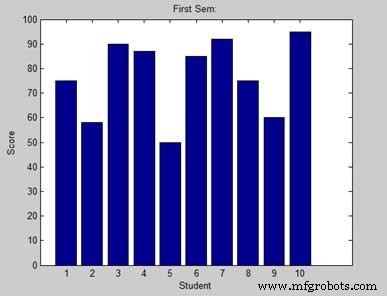
Tengamos un salón de clases imaginario con 10 estudiantes. Sabemos que el porcentaje de calificaciones obtenidas por estos estudiantes es 75, 58, 90, 87, 50, 85, 92, 75, 60 y 95. Dibujaremos el gráfico de barras para estos datos.

Cree un archivo de script y escriba el siguiente código −

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente gráfico de barras −

Dibujo de contornos

Una línea de contorno de una función de dos variables es una curva a lo largo de la cual la función tiene un valor constante. Las curvas de nivel se utilizan para crear mapas de contorno uniendo puntos de igual elevación por encima de un nivel determinado, como el nivel medio del mar.

MATLAB proporciona un contorno función para dibujar mapas de contorno.

Ejemplo

Generemos un mapa de contorno que muestre las líneas de contorno para una función dada g =f(x, y). Esta función tiene dos variables. Entonces, tendremos que generar dos variables independientes, es decir, dos conjuntos de datos x e y. Esto se hace llamando al meshgrid comando.

La red de malla El comando se usa para generar una matriz de elementos que dan el rango sobre x e y junto con la especificación del incremento en cada caso.

Tracemos nuestra función g =f(x, y), donde −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Tomemos un incremento de 0,1 para ambos valores. Las variables se establecen como −

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

Por último, necesitamos asignar la función. Sea nuestra función:x ² + y ²

Cree un archivo de script y escriba el siguiente código −

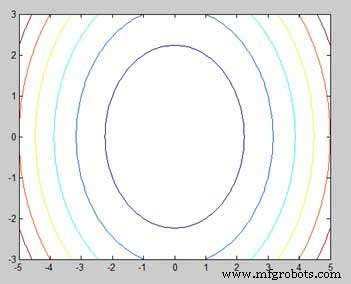
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
contour(x,y,g)                         % call the contour function
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente mapa de contorno −

Modifiquemos un poco el código para arreglar el mapa

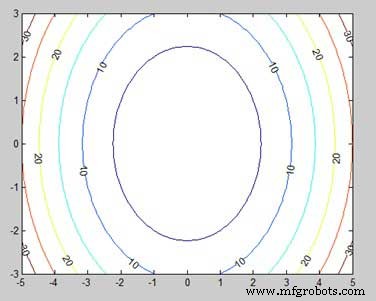
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente mapa de contorno −

Gráficas Tridimensionales

Los gráficos tridimensionales básicamente muestran una superficie definida por una función en dos variables, g =f (x,y).

Como antes, para definir g, primero creamos un conjunto de puntos (x,y) sobre el dominio de la función usando meshgrid dominio. A continuación, asignamos la función en sí. Finalmente, usamos el surf comando para crear un gráfico de superficie.

El siguiente ejemplo demuestra el concepto −

Ejemplo

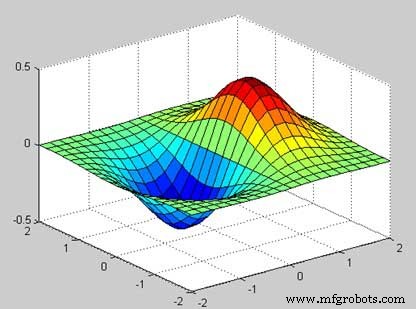
Vamos a crear un mapa de superficie 3D para la función g =xe ^{-(x 2 + y 2 )}

Cree un archivo de script y escriba el siguiente código −

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Cuando ejecuta el archivo, MATLAB muestra el siguiente mapa 3-D −

También puedes usar la malla comando para generar una superficie tridimensional. Sin embargo, el surf El comando muestra tanto las líneas de conexión como las caras de la superficie en color, mientras que la malla El comando crea una superficie de estructura alámbrica con líneas de colores que conectan los puntos de definición.