Propiedades electrónicas de la butaca Nanocintas de fosforo negro modificadas en los bordes por los elementos de transición V, Cr y Mn

Resumen

Las propiedades estructurales, eléctricas y magnéticas de las nanocintas de fosforeno negro de sillón (APNR) funcionalizadas en los bordes por elementos de metal de transición (TM) V, Cr y Mn se estudiaron mediante la teoría de la función de densidad combinada con la función de Green de no equilibrio. Los estados de borde con polarización de espín introducen una gran variedad de estructuras electrónicas de TM-APNR. Para los APNR con borde cosido con Mn, sus estructuras de banda exhiben propiedades eléctricas de semiconductores en estado ferromagnético. Un campo eléctrico transversal puede hacer que los Mn-APNR sean metálicos cambiando las bandas de conducción de los estados de los bordes a través del efecto Stark. La heterounión Mn / Cr-APNR puede usarse para fabricar espín p-n diodo donde la rectificación fuerte actúa solo en un giro.

Introducción

El descubrimiento del grafeno [1, 2] ha desencadenado un aumento de la investigación de materiales cristalinos bidimensionales (2D) [3,4,5,6]. En la última década, se han preparado o predicho nitruro de boro hexagonal, dicalcogenuro de metal de transición, fosforeno negro y muchos otros [7, 8, 9]. Esos materiales 2D se pueden implementar en una amplia gama de campos, importantes no solo para explorar nuevos fenómenos físicos y rendimiento por debajo del límite 2D, sino también para muchas aplicaciones novedosas en dispositivos electrónicos, espintrónicos y optoelectrónicos [10,11,12,13 , 14,15,16,17,18,19,20,21]. Además, algunas propiedades de los materiales bidimensionales pueden mejorarse después de adaptarse a nanocintas unidimensionales (1D) y / o funcionalizarse [22, 23]. Se ha observado un rendimiento excelente en transistores de efecto de campo de nanocintas de grafeno sintetizadas ascendentes [24]. Se han predicho contactos sin barrera de Schottky con semiconductores 2D a través de carburo metálico o nitruro funcionalizado por grupos O u OH [25]. Se han propuesto nanoflakes de fosforeno con bordes modificados para células solares de alta eficiencia [26]. Pueden emplearse defectos atómicos e impurezas para modular localmente las propiedades electrónicas para aplicaciones potenciales en magnetismo y catálisis [27, 28, 29]. La aplicación de campo eléctrico externo y heteroestructuras puede manipular aún más de manera significativa las propiedades electrónicas [30, 31, 32].

Entre los materiales 2D conocidos, el fosforeno negro es uno de los pocos con propiedades mecánicas, eléctricas y ópticas superiores para aplicaciones de dispositivos. Desde la fabricación de transistores de efecto de campo basados en él [9], el fosforeno negro ha atraído cada vez más interés. Es un semiconductor directo con un intervalo de banda modesto (≈ 2 eV) y una gran movilidad de orificios (≈ 1000 cm ² / (Vs)) [33,34,35], mostrando un enorme potencial de aplicación en los campos de la electrónica, optoelectrónica, sensores, catálisis y baterías [36,37,38,39]. Similar al grafeno, el fosforeno negro se puede cortar en dos direcciones típicas en nanocintas de fosforeno en zigzag (ZPNR) o nanocintas de fosforo de sillón (APNR) [40,41,42]. La simulación de los primeros principios ha demostrado que el dopaje sustitutivo del metal de transición puede introducir fácilmente magnetismo en el fosforeno para aplicaciones espintrónicas [43]. La absorción de metales de transición, anclados por defectos, podría dar lugar a sistemas de fosforeno compuestos metálicos y semimetálicos [44]. Se ha predicho que la modificación de los bordes del metal de transición también puede modular en gran medida las propiedades electrónicas de las nanocintas de fosforeno en zigzag [45]. Sin embargo, hasta donde sabemos, los efectos de la pasivación de la MT en los APNR aún no se han estudiado bien.

En este artículo, nos centramos en la modulación de las propiedades electrónicas de los APNR funcionalizados por los elementos metálicos de transición típicos V, Cr y Mn, ya que introducen momentos magnéticos más grandes que los demás. Las simulaciones basadas en la teoría funcional de la densidad muestran que el comportamiento del semiconductor puede aparecer y puede ser controlado por un campo eléctrico transversal. Además, giro de alto rendimiento p-n La unión puede diseñarse para aplicaciones espintrónicas [46].

Sistemas y métodos computacionales

El fósforo negro es un material en capas en el que las capas atómicas se apilan juntas por una fuerza de van der Waals débil entre capas, mientras que los átomos en cada capa están unidos por fuertes enlaces covalentes. Puede desprenderse fácilmente en fosforanos monocapa. La vista superior de un fosforeno se esquematiza en la Fig. 1a con una parte ampliada en su lado derecho para mostrar los parámetros geométricos. Además, se dan dos vistas laterales a lo largo del sillón y direcciones en zigzag, respectivamente. Cada átomo de fósforo está unido a tres átomos de fósforo adyacentes (con constantes de red de 3,31 y 4,38 Å, longitud de enlace 2,2 Å, ángulo de enlace 96,34 ° y ángulo diedro 102,1 °) para formar una estructura de panal plisada [47]. Al igual que otros materiales bidimensionales de celosía de panal hexagonal como el grafeno y el disulfuro de molibdeno, un fosforeno se puede adaptar a nanocintas con dos morfologías de borde típicas, el sillón y nanocintas de fosforo negro en zigzag [40, 41, 48, 49].

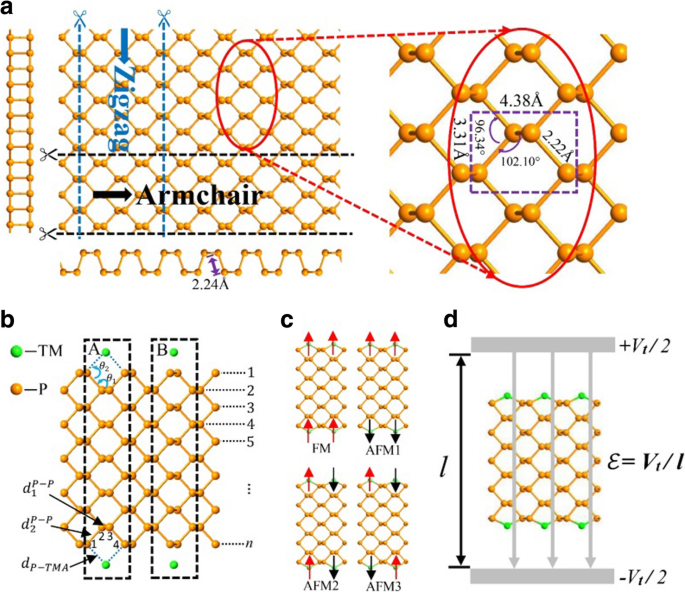
un Vistas superior y lateral de un fosforeno 2D con una vista ampliada en el lado derecho. Las vistas en sección transversal del sillón y los bordes en zigzag se muestran a continuación y en el lado izquierdo, respectivamente. b Un APNR con TM adatoms en sitios huecos (A) y sitios superiores (B) en el borde. Los marcos discontinuos indican el tamaño de la celda primitiva y el número n denota el ancho de nanocintas. c Las cuatro configuraciones magnéticas de APNR. d El diagrama esquemático en presencia de un campo eléctrico transversal

Aquí, consideramos el semiconductor n -APNR para números de ancho impar n con sección transversal simétrica de espejo. Deberían producirse resultados similares incluso para n ya que los dos bordes de la nanocinta son casi independientes, como se describe a continuación. Los efectos de las modificaciones de los bordes por tres elementos típicos de metales de transición (TM) V, Cr y Mn se analizan sistemáticamente. Como se ilustra en la Fig. 1b, un átomo de TM puede adsorberse en un borde APNR en la posición hueca (caso A) o en la posición superior (caso B). Dado que el caso A tiene una energía de enlace mucho mayor, lo adoptamos cuando un átomo de TM se adsorbe cerca del centro de cada posición hueca y se une a los dos átomos del borde de fósforo además. Para facilitar la descripción de la geometría de unión de los átomos de TM en los bordes APNR, como se ilustra en la Fig. 1b, indicamos los átomos de fósforo en los sitios 1, 2, 3 y 4 como P ₁ , P ₂ , P ₃ y P ₄ , respectivamente. También definimos algunos parámetros geométricos:las longitudes de enlace \ ({d} _1 ^ {P-P} \) (entre P ₂ y P ₃ ), \ ({d} _2 ^ {P-P} \) (entre P ₁ , P ₂ o P ₃ , P ₄ ) y d ^{P - TM} y los ángulos de enlace θ ₁ (entre \ ({d} _1 ^ {P-P} \) y \ ({d} _2 ^ {P-P} \)) y θ ₂ (entre \ ({d} _2 ^ {P-P} \) y d ^{P - TM} ). Debido al magnetismo de los adatoms TM, hay cuatro configuraciones magnéticas posibles, es decir, FM, AFM1, AFM2 y AFM3 como se muestra en la Fig. 1c. En ausencia de campo magnético, nuestra simulación muestra que la energía de la celda unitaria AFM2 en la Fig. 1c es aproximadamente 0.2 eV menor que la de la FM. Los dos bordes son casi independientes y la polarización de espín opuesta entre ellos en las configuraciones AFM1 y AFM3 puede reducir la energía en una cantidad inferior a 0,002 eV. En este artículo, estudiamos las propiedades electrónicas de las nanocintas en la configuración FM, ya que un campo magnético aplicado puede mantenerlas así. También estudiamos los efectos de un campo eléctrico transversal aplicado, como se ilustra en la Fig. 1d, sobre la estructura electrónica y las propiedades de los APNR de FM. Finalmente, proponemos posibles aplicaciones de dispositivos de los materiales.

Las propiedades de transporte de una unión de nanocintas se calculan estableciendo una estructura de dispositivo de dos sondas. La unión está dividida en tres partes:Una región de dispersión, donde se encuentra la interfaz de unión, está intercalada entre los electrodos izquierdo (L) y derecho (R). Cuando una polarización de voltaje V _b se aplica entre los dos electrodos, establecemos las energías de Fermi en los electrodos L y R como μ _L =- e | V _b | / 2 y μ _R = e | V _b | / 2. La corriente electrónica de espín σ a través de los dispositivos cuánticos se evalúa mediante la fórmula de Landauer-Büttiker [50]:

$$ {I} _ {\ sigma} =\ frac {e} {h} \ underset {- \ infty} {\ overset {\ infty} {\ int}} {T} _ {\ sigma} (E) \ izquierda [f \ izquierda (E - {\ mu} _ {\ mathrm {R}} \ derecha) -f \ izquierda (E - {\ mu} _ {\ mathrm {L}} \ derecha) \ derecha] dE $ $ (1)

Aquí, T _σ ( E ) es la transmisión de espín σ y f la función de distribución de Fermi-Dirac.

La simulación se realiza mediante el paquete Atomistix toolkits (ATK) basado en la teoría funcional de densidad ab initio (DFT) combinada con el método de función de Green en no equilibrio (NEGF) [51, 52]. Antes de la estructura electrónica y las simulaciones de transporte, las estructuras se optimizan hasta que las fuerzas que actúan sobre cada átomo son inferiores a 0,02 eV / Å. Usamos la aproximación de gradiente generalizado dependiente de espín con la parametrización de Perdew-Burke-Emzerhof (SGGA-PBE) para la función de correlación de intercambio. Hemos confirmado que las simulaciones SGGA + U conducen al mismo resultado que se presenta a continuación [43]. Un conjunto básico de doble polarización zeta ( dzp ) orbitales atómicos se utiliza en el cálculo para obtener un resultado preciso. Se inserta una capa de vacío de 20 Å de espesor entre nanocintas vecinas para evitar acoplamientos entre cintas. La energía de truncamiento para la expansión del vector base de las funciones de onda se establece en 150 Hartree o 4082 eV con un k -rejilla de malla espacial de 1 × 1 × 101. Se adopta una temperatura electrónica de 300 K en la técnica de integración del eje real para el esquema NEGF para facilitar la simulación. Las cuatro configuraciones magnéticas se obtienen estableciendo inicialmente las polarizaciones de espín correspondientes de los adatomos TM antes de la optimización. El campo eléctrico transversal ε es generado por dos placas metálicas virtuales paralelas, separadas por una distancia l , con una diferencia de potencial eléctrico V _t entonces ε =V _t / l .

Resultados y discusión

Geometría y energía de unión

En los APNR prístinos, los átomos del borde P se desplazan a la posición hueca de modo que cada "sillón" de borde se vuelve más estrecho en comparación con su contraparte 2D, como se muestra en la Fig. 2a, b. Si un APNR se hidrogena con el enlace de suspensión de cada átomo de P del borde saturado por un átomo de H como se indica en la Ref. [48, 53], los átomos del borde P se recuperan a sus posiciones 2D, como se ilustra en la Fig. 2c. Cuando un átomo de TM se adsorbe en cada posición hueca, pasiva además los dos átomos de P del borde. Luego, los sillones se recuperan parcialmente y los bordes se magnetizan debido a la polarización de giro de los adatomos TM. En la configuración FM, no se observa ninguna reconstrucción en los bordes y la longitud de la celda primitiva permanece sin cambios como se indica en la Fig. 2d-f.

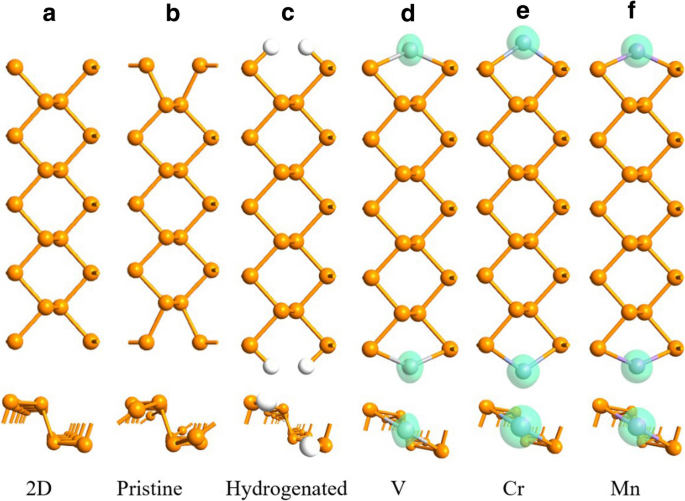
Geometrías de FM 9-APNR a recién cortado de un fosforeno 2D, b geométricamente optimizado (prístino), c hidrogenado, y después de adsorber d V, e Cr y f Mn átomos en el borde. La densidad de polarización de espín de los átomos se muestra en la isosuperficie verde con un valor de 0,004 e / Å ³

En la Tabla 1, enumeramos los parámetros geométricos y la energía de enlace E _b para 9- y 17-APNR prístinos, hidrogenados y que adsorben TM en la configuración FM, si corresponde. Aquí, E _b =( mE _X + E _APNR - E _{X - APNR} ) / m con E _X , E _APNR y E _{X - APNR} las energías totales de un átomo externo, una célula primitiva de APNR prístino y una célula primitiva de APNR pasivada por m átomos externos, respectivamente, con m =4 para H y m =2 para elementos TM. Cuando cortamos un fosforeno 2D para hacer un APNR, los enlaces de suspensión en el borde se reducen significativamente θ ₁ de 102 a 87 °. La pasivación de los enlaces en suspensión por átomos externos se recupera θ ₁ e introduce una reacción repulsiva, marcada por el tramo de \ ({d} _ {P-P} ^ 1 \) y \ ({d} _ {P-P} ^ 2 \). En los casos de TM, la adsorción de átomos de V muestra la reacción repulsiva más fuerte con la mayor θ ₁ . Similar a la de H, la adsorción del elemento TM es energéticamente estable con una energía de enlace del orden de 4 eV. Los dos bordes de APNR son casi independientes entre sí, por lo que los parámetros de geometría y E _b son insensibles al ancho de APNR. La geometría de unión y la energía se mantienen también en diferentes configuraciones magnéticas para TM- n -APNRs.

Estructura electrónica y propiedades magnéticas

En la Fig. 3, presentamos las estructuras de bandas y las funciones de onda típicas de los electrones en 9-APNR con y sin modificación de bordes. Los APNR prístinos son semiconductores indirectos no magnéticos con una banda prohibida de E _g ≈ 0.5 eV, donde los estados electrónicos en la parte superior (inferior) de la banda de valencia (conducción) son estados generales (borde). Cuando los átomos de borde P son pasivados por átomos de H, la banda de conducción debido a los enlaces de suspensión de borde en APNR prístinos se aleja de la banda prohibida y los ANPR hidrogenados se convierten en semiconductores directos con una banda prohibida más amplia de E _g ≈ 1,0 eV. Los estados en la parte inferior de la banda de conducción y en la parte superior de la banda de valencia son todos estados generales. A medida que aumenta el ancho de n =9 a 17, la banda prohibida disminuye ligeramente de 1,01 a 0,89 eV de acuerdo con los pronosticados por Han et al. [49].

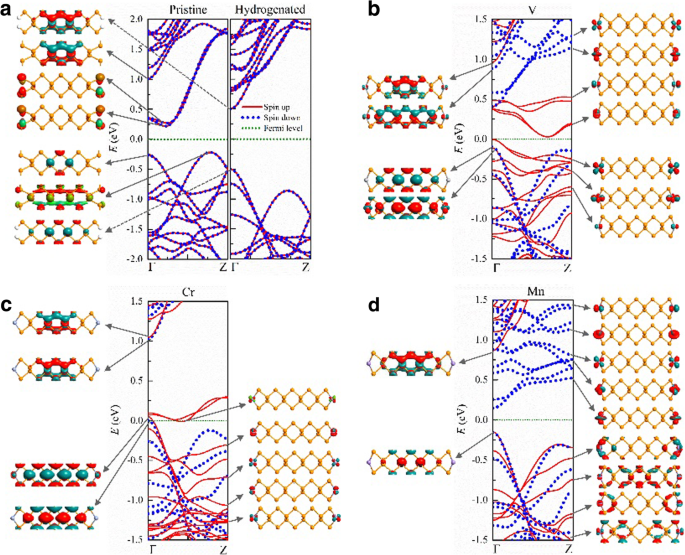
Estructuras de bandas y funciones de onda típicas cerca de la energía de Fermi de los 9-APNR prístinos modificados en el borde por a H, b V, c Cr y d Mn átomos

Cuando los átomos de TM se adsorben en los bordes de los APNR, permanecen polarizados en el espín. En la configuración de FM, V- n -Los APNR son semiconductores magnéticos con banda prohibida dependiente del espín. Como se ilustra en la Fig. 3b, para n =9, los electrones de spin-up tienen una brecha indirecta de \ ({E} _g ^ {\ mathrm {up}} \ approx 0.03 \) eV mientras que los electrones de spin-down tienen una brecha directa de \ ({E} _g ^ {\ mathrm {abajo}} \ aproximadamente 0,5 \) eV. Los estados electrónicos en las bandas giratorias alrededor de la energía de Fermi se componen de d orbitales de los V adatomos y están confinados en los bordes. Esas bandas de borde giratorias tienen una dispersión similar y están parcialmente ocupadas. La parte superior de la banda de valencia correspondiente y la parte inferior de la banda de conducción se separan en k espacio pero están cerca uno del otro en energía. Aparece una banda prohibida indirecta estrecha para los electrones de spin-up. Por el contrario, todas las bandas de borde giratorias están muy por encima de la energía de Fermi. La banda de valencia de spin-down proviene de estados generales y tiene una dispersión opuesta a la banda de conducción de spin-down que proviene de estados de borde. Esto da como resultado la banda prohibida directa para los electrones de spin-down. Las bandas del borde V aparecen en pares debido al acoplamiento débil entre los átomos V del borde izquierdo y derecho. Tres de los cinco pares están ocupados, por lo que cada celda primitiva tiene un momento magnético de 6 μ _B .

Un par de spin-up y todos los spin-down d Las bandas del borde orbital están ubicadas por encima del nivel de Fermi en Cr-9-APNR como se ilustra en la Fig. 3c, porque hay cuatro d electrones orbitales en cada átomo de Cr. Debido a la ligera superposición de los dos pares más altos de bandas de borde de giro hacia arriba cerca de la parte superior de la banda de valencia de giro hacia abajo, se convierte en un medio metal con el nivel de Fermi justo por encima de la parte superior de la banda de valencia de giro hacia abajo. En Mn-9-APNR, los cinco pares de spin-up d las bandas orbitales están ocupadas mientras el spin-down d las bandas orbitales están vacías como se muestra en la Fig. 3d. Se convierte en un medio semiconductor donde los espacios de banda de espines opuestos difieren enormemente, con \ ({E} _g ^ {\ mathrm {up}} \ approx 1 \) eV para spin-up y \ ({E} _g ^ {\ mathrm {down}} \ approx 0.3 \) eV para spin-down. Ambos giros tienen la misma parte superior de la banda de valencia en la que se encuentran los estados generales. Sin embargo, la parte inferior de la banda de conducción del spin-down es mucho más baja que la del spin-up debido a los estados de borde de spin-down desocupados.

Las estructuras electrónicas de TM- n -Las APNR siguen siendo el mismo patrón y no cambian tanto como n aumenta como se ilustra en la Fig. 4. Sin embargo, las propiedades físicas pueden variar significativamente en las muestras pasivadas con Cr porque una brecha de energía puede abrirse como n aumenta. Estrecho Cr- n -Las APNR son mitad metálicas, pero anchas Cr- n -Los APNR pueden convertirse en semiconductores como se muestra en los recuadros de la Fig. 4 para n =11 y n =17, respectivamente.

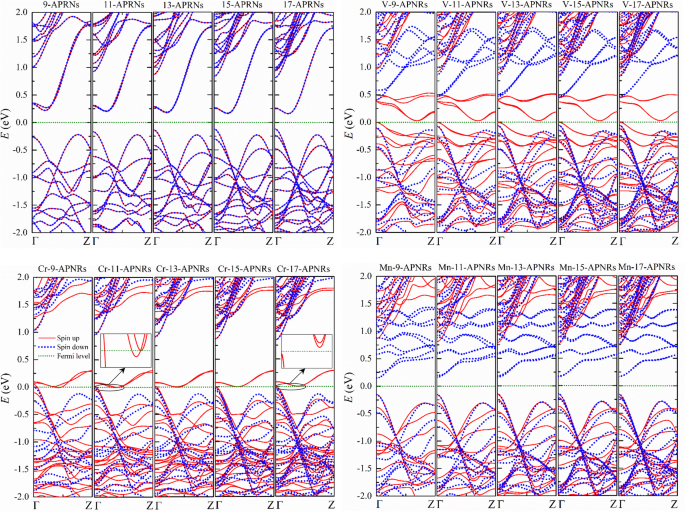
Estructuras de bandas de prístina n -APNR y los modificados en el borde por átomos de V, Cr y Mn para varios n . Vistas ampliadas de Cr- n -Las APNR cerca del nivel de Fermi se muestran en los recuadros para n =11 y 17

Los perfiles de distribución de momento magnético de FM TM-9-APNR se muestran en la Fig.2, donde las isosuperficies de la densidad de espín ∆ρ = ρ ^arriba - ρ ^abajo =0,004 e / Å ³ están trazados. Aquí, ρ ^arriba y ρ ^abajo son las densidades de los electrones de spin-up y spin-down, respectivamente. Los momentos magnéticos se concentran principalmente alrededor de los átomos de TM y la contribución de los átomos de P es demasiado pequeña para mostrarse con claridad. En la Tabla 2, presentamos el momento magnético total M _T en una celda primitiva, la suma de momentos de los diez átomos del borde M _E =2 M (TM) + 4 M (P ₁ ) + 4 M (P ₂ ), y el momento de un átomo de borde único TM, P ₁ / P ₄ , o P ₂ / P ₃ .

Los momentos magnéticos totales provienen principalmente de los átomos del borde ( M _T ≈ M _E ) y en unidades de μ _B por celda primitiva están cerca de los números de electrones de valencia de los átomos del metal de transición menos 4. En V- n -APNRs, los átomos de borde P (P ₁ y P ₄ ) están polarizados ligeramente en antiparalelo mientras que los átomos de P del segundo borde (P ₂ y P ₃ ) están polarizados en paralelo. Entonces, los momentos magnéticos de los átomos de P casi se cancelan entre sí. Cada átomo de V tiene un momento magnético de aproximadamente 3 μ _B de tres 3 d orbitales. Los 4 s El orbital está completamente ocupado de forma similar a un solo átomo de V. En contraste, los átomos de borde P en Cr- n -Las APNR tienen momentos magnéticos mucho más grandes de M (P1) ≈ - 0,27 μ _B . Coincidentemente, tienen el d más largo ^{P - TM} entre los tres TM-APNR, lo que indica también la mayor desviación geométrica de los átomos de P de los del fosforeno 2D. Además, cada átomo de Cr tiene un momento magnético de aproximadamente 5 μ _B , en lugar de 4 μ _B . Esto sugiere que sus 4 s El orbital no está completamente ocupado y contribuye a la polarización del espín, similar al caso del átomo de Cr aislado que tiene una configuración de electrones de valencia de 3 d ⁵ 4 s ¹ . Los s con polarización de espín Los orbitales de átomos de Cr en Cr-APNR podrían haber inducido la polarización de espín antiparalelo en el p orbitales en sus átomos de P vecinos a través del mecanismo de intercambio cinético. En Mn- n -APNR, el d los orbitales del átomo de Mn están ocupados a la mitad con un momento magnético de aproximadamente 5 μ _B y los átomos de P vecinos están todos polarizados en paralelo muy débilmente. En la Fig.5, trazamos la densidad parcial de estados (PDOS) (azul) de d orbitales en átomos de TM junto con la densidad total de estados (DOS) (negro) de los 9-APNR. Aquí, el giro se divide y la energía se propaga de d los orbitales se muestran claramente. En los APNR prístinos e hidrogenados, los espectros DOS de giro hacia arriba y hacia abajo se superponen entre sí, lo que indica que no hay polarización de giro. En TM-APNR, el spin-up y el spin-down d Los espectros de PDOS orbitales se distribuyen principalmente en un rango de energía de 2 a 4 eV. Están bien separados en energía con una separación de aproximadamente 3, 9 y 4 eV en V-, Cr- y Mn-APNR, respectivamente. Excluyendo el d orbitales, el p Los orbitales de los átomos de P dominan la contribución al DOS de las bandas de valencia. Tenga en cuenta que las s Los orbitales de átomos de Cr también contribuyen significativamente en Cr-APNR. La pasivación de los bordes de los átomos de Co y Ni también puede introducir magnetismo en los APNR, pero el magnetismo introducido por otros elementos de TM como Sc, Ti, Fe, Cu y Zn puede ser bastante limitado.

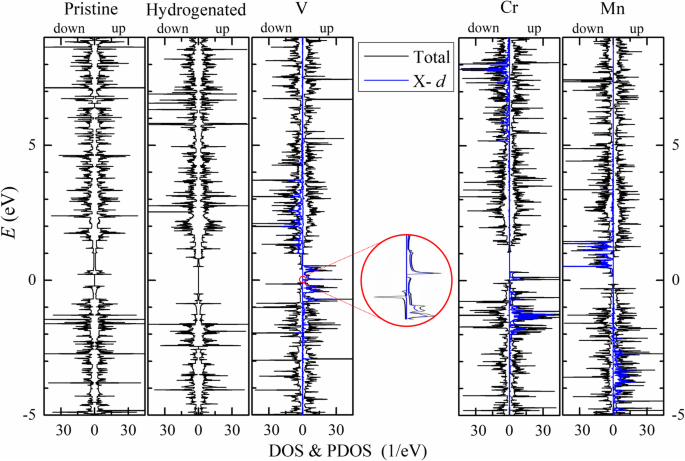
El DOS (curva negra) de los 9-APNR prístinos y modificados en su estado FM se traza para el giro hacia arriba (derecha) y el giro hacia abajo (izquierda). El d También se presenta para comparación la PDOS orbital (curva azul) de los átomos de TM. El DOS de V-9-APNR cerca de la energía de Fermi se amplía en el recuadro para mostrar la banda prohibida

Efectos de un campo eléctrico transversal

El campo eléctrico transversal se ha empleado ampliamente en dispositivos electrónicos para controlar la concentración de portadores y la estructura de bandas de los semiconductores [54, 55]. Como se indica en la Fig. 1d, simulamos las estructuras electrónicas de TM- n -APNR en la configuración FM bajo un campo eléctrico transversal \ (\ mathcal {E} ={V} _t / l \) paralelo al plano de nanocintas, mediante nanocintas intercaladas entre dos barras paralelas. Aquí, V _t es la diferencia de voltaje entre las dos barras y l es la separación entre ellos. Debido al efecto Stark, dos estados degenerados separados en el espacio real por una distancia Δ a lo largo del campo eléctrico deberían dividirse en una cantidad de \ (\ delta E =e {\ mathcal {E}} ^ {\ ast} \ Delta \) , donde el campo eléctrico efectivo \ ({\ mathcal {E}} ^ {\ ast} \) suele ser más pequeño que el campo eléctrico externo \ (\ mathcal {E} \) como resultado del efecto de apantallamiento. En TM- n -APNR, la distancia Δ entre los centros de estado de un par de borde-banda puede ser tanto como el ancho de nanocintas si cada estado está confinado solo en un borde, pero Δ debería ser más corto o incluso desaparecer para estados de borde mixtos. Como se ilustra en las funciones de onda de la Fig. 3, los estados de los bordes suelen estar mezclados.

En la Fig. 6, presentamos las estructuras de bandas de V-, Cr- y Mn-13-APNR para varios \ (\ mathcal {E} \). El ancho de la nanocinta es aproximadamente \ (w =0.5 \ left (n-1 \ right) \ times 3.31 \ {\ AA} + {d} ^ {P- \ mathrm {TM}} \ cos \ left ({135} ^ {{} ^ {\ circ}} - {\ theta} _2 \ right) \ approx 21 \ kern0.20em {\ AA}. \) La división de Stark es mucho más pequeña que \ (e \ mathcal {E} w \) indica un fuerte efecto de tramado o una fuerte mezcla de los estados de los bordes. Dado que V-13-APNR tiene un intervalo de banda de giro muy estrecho, se vuelve medio metálico a aproximadamente \ (\ mathcal {E} =3 \) V / nm. La división de Stark de las bandas de borde de conducción puede llegar a 0.1 eV a \ (\ mathcal {E} =5 \) V / nm. Cr-13-APNR muestra una fuerza similar de división de Stark y permanece medio metálico bajo el campo transversal.

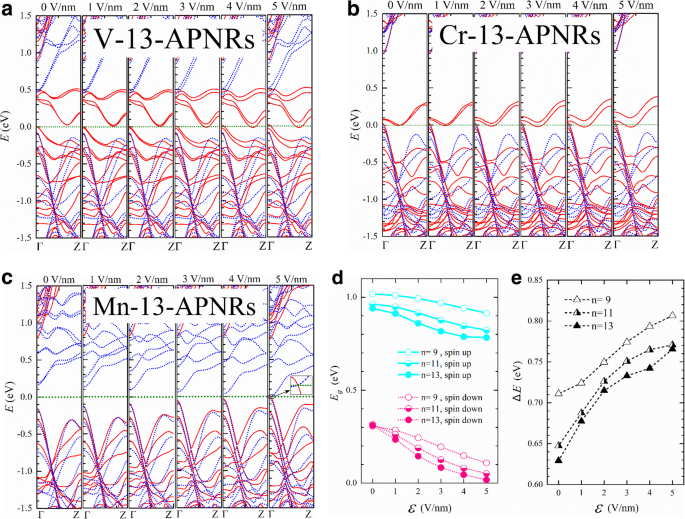
Las estructuras de bandas giratorias (sólidas) y descendentes (punteadas) de a V-, b Cr- y c Mn-13-APNR bajo un campo eléctrico transversal de fuerza \ (\ mathcal {E} =0,1, \ dots, 5 \) V / nm. d Los huecos de banda de Mn- n -APNR versus \ (\ mathcal {E} \) para giro hacia arriba (\ ({E} _g ^ {\ mathrm {arriba}} \), líneas continuas) y giro hacia abajo (\ ({E} _g ^ {\ mathrm {abajo}} \), líneas de puntos) con n =9, 11 y 13. e La diferencia de brecha \ (\ Delta E ={E} _g ^ {\ mathrm {up}} - {E} _g ^ {\ mathrm {down}} \) versus \ (\ mathcal {E} \)

Se observa un efecto Stark mucho más fuerte en el semiconductor Mn-13-APNR como se muestra en la Fig. 6c. Los pares de estados de borde de bandas de conducción descendente obtienen una división de aproximadamente 0,55 eV en el punto Γ en k espacio debajo de \ (\ mathcal {E} =5 \) V / nm. La banda de conducción de spin-down se superpone con la banda de valencia de spin-up, y el Mn-13-APNR pasa de un semiconductor a un metal como se ilustra en el recuadro ampliado. En la Fig. 6d, graficamos las brechas de energía de giro hacia arriba y hacia abajo frente a la intensidad del campo. Las funciones de onda de los electrones cambian con el campo y las brechas de energía no varían linealmente con el campo. La banda prohibida de Mn-13-APNR casi desaparece en \ (\ mathcal {E} =5 \) V / nm para los electrones de spin-down, pero permanece por encima de 0,75 eV para los electrones de spin-up. La diferencia de brecha de energía ∆E entre los giros opuestos se representa frente a \ (\ mathcal {E} \) en la Fig. 6e para n =9, 11 y 13. ∆E aumenta en un paso mucho más lento para n =9 que para n =11 y 13 en el campo bajo, pero la forma se invierte en el campo alto.

Girar p-n Cruce

Hemos visto que los átomos de TM pueden modular la estructura de bandas de los APNR de varias formas. Esto ofrece oportunidades para el diseño de dispositivos novedosos. Por ejemplo, podemos combinar Cr-APNR y Mn-APNR para formar un p-n dependiente de espín. unión. Experimentalmente, está disponible el dopado con iones metálicos [56] en fosforeno. También se pueden realizar costuras suaves de materiales 2D [57] y modificación del borde atómico de nanocintas [58]. Esas técnicas podrían usarse para fabricar el p-n unión. En la Fig. 7a, graficamos su voltaje de corriente ( I-V ) característica obtenida de la simulación del sistema de dos sondas que se muestra en el recuadro superior. El giro p-n La unión muestra un efecto de rectificación muy fuerte para los electrones de spin-up, pero solo un efecto débil para los electrones de spin-down. Esta dependencia del giro proviene de las estructuras de bandas distinguidas de los electrodos izquierdo y derecho, como se ilustra en el recuadro inferior. Bajo sesgo negativo, el electrodo de Mn-APNR izquierdo tiene una energía de Fermi μ _L = e | V _b | / 2 y el Cr-APNR μ derecho _R =- e | V _b | / 2. Dentro de la ventana de transporte del rango de energía [ μ _L , μ _R ], solo hay una parte muy pequeña de la banda de energía de descenso en el electrodo Cr-APNR, por lo que la corriente de descenso permanece baja. Por el contrario, existe una amplia superposición de las bandas de energía de giro tanto en los electrodos de Mn como en los de Cr-APNR y la corriente de giro aumenta rápidamente con la polarización. Dentro de la ventana de transporte [ μ _R , μ _L ] bajo sesgo positivo, sin embargo, no hay banda de energía de giro en el electrodo izquierdo y la corriente correspondiente permanece casi cero ya que Mn-APNR es un p de tipo semiconductor de amplio espacio para un giro ascendente. La corriente de descenso comienza a aumentar en V _b =0,2 V cuando la energía de Fermi derecha se alinea con la banda de conducción de giro descendente izquierda. En la Fig. 7b, graficamos la relación de rectificación α _σ =[ yo _σ (- | V _b |) - yo _σ (| V _b |)] / yo _σ (| V _b |) de giro σ en función de la magnitud del sesgo | V _b |. En | V _b | =0.5 V, el giro APNR p-n La unión tiene una rectificación de 2400 para giro ascendente y solo 2 para giro descendente.

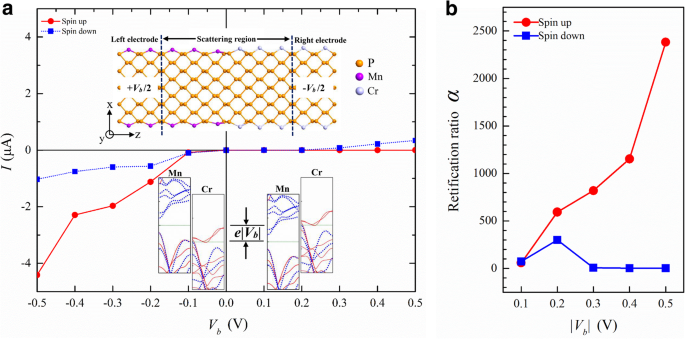
un El I-V dependiente del giro característica de una heterounión Mn / Cr-9-APNR. La geometría del sistema de dos sondas se muestra en el recuadro superior. Los recuadros inferiores esquematizan las alineaciones de las bandas de energía de los electrodos para polarizaciones negativas y positivas. b La relación de rectificación correspondiente α se traza frente a la magnitud del sesgo

Conclusiones

La simulación DFT-NEGF sugiere que la funcionalización de borde de los átomos de TM puede manipular en gran medida las propiedades eléctricas y magnéticas de los APNR de semiconductores no magnéticos y convertirlos en semiconductores metálicos o semiconductores. Los átomos de TM en TM-APNR mantienen sus configuraciones electrónicas en un estado aislado donde el magnetismo de los átomos de V y Mn proviene principalmente de d orbitales pero el de Cr de ambos d y s orbitales. En Mn-APNR, el d los orbitales están medio llenos. Todo el spin-up d los orbitales de los átomos de Mn están ocupados y el spin-down d los orbitales están por encima del nivel de Fermi. Debido a la estrecha banda prohibida de d orbital, los Mn-APNR se convierten en semiconductores donde las bandas de energía de giro hacia abajo tienen un espacio mucho más estrecho en el nivel de Fermi que las de giro hacia arriba. Esta propiedad peculiar podría emplearse para el diseño de dispositivos espintrónicos, ya que los materiales pueden ser semiconductores para un espín y aislantes para el otro en condiciones adecuadas. Con la ayuda del efecto Stark en los estados de borde, las brechas de energía se pueden modular aún más mediante un campo eléctrico transversal aplicado. Por ejemplo, un campo de 5 V / nm puede cerrar la banda prohibida de los electrones de spin-down mientras mantiene un gap de 0,75 eV para los electrones de spin-up. Aprovechando la drástica diferencia de banda de energía entre Mn- y Cr-APNR, podemos diseñar spin p-n diodos de unión Mn / Cr-APNR en los que se produce una rectificación fuerte solo para un giro.

Abreviaturas

1D:: Unidimensional
2D:: Dos dimensiones
AFM:: Antiferromagnético
APNR:: Sillón nanociné fosforeno negro
ATK:: Conjuntos de herramientas de Atomistix
DFT:: Teoría funcional de la densidad
DOS:: Densidad de estados
FM:: Ferromagnético
NEGF:: Función de Green fuera de equilibrio
TM:: Metal de transición

WO3 / p-Type-GR Materiales estratificados para la degradación fotocatalítica de antibióticos promocionada y dispositivo para la percepción del mecanismo Conversión de fotoconductividad positiva y negativa inducida por adsorción de moléculas de H2O en nanocables WO3

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias