Estudio de espectroscopia Raman y difracción de rayos X de alta presión in situ de Ti3C2Tx MXene

Resultados y discusiones

Antes de realizar mediciones de alta presión, primero investigamos las propiedades básicas del material del Ti ₃ exfoliado C ₂ T _x Copos de Mxene. Una imagen óptica del Ti ₃ exfoliado C ₂ T _x escamas depositadas sobre Si / SiO ₂ (300 nm) el sustrato se muestra en la Fig. 1a. Se puede observar un contraste verde claro para las escamas exfoliadas. Según lo informado por Miranda et al., El contraste óptico de Ti ₃ C ₂ T _x las escamas dependen en gran medida del grosor de las escamas, donde las escamas más gruesas siempre muestran un mayor contraste, mientras que las escamas delgadas exhiben un bajo contraste [25]. El contraste de color verde claro de la mayoría de las escamas en la Fig. 1b indica su espesor delgado. Una imagen topográfica de microscopio de fuerza atómica (AFM) de Ti ₃ exfoliado C ₂ T _x las escamas se muestran en la Fig. 1b. Las escamas en el área de mapeo muestran superficies con alta rugosidad, que es típica de Ti ₃ C ₂ T _x copos [26]. El grosor de una escama delgada típica se puede determinar a partir de su perfil de línea (recuadro de la figura 1b) a través de la posición marcada en la figura 1b para que sea de 170 nm. En la figura 1c se muestra una imagen de microscopio electrónico de barrido (SEM) de una escama exfoliada. La estructura laminada de Ti ₃ C ₂ T _x se puede ver claramente, lo que indica la preparación exitosa de Ti ₃ C ₂ T _x muestras en capas [10].

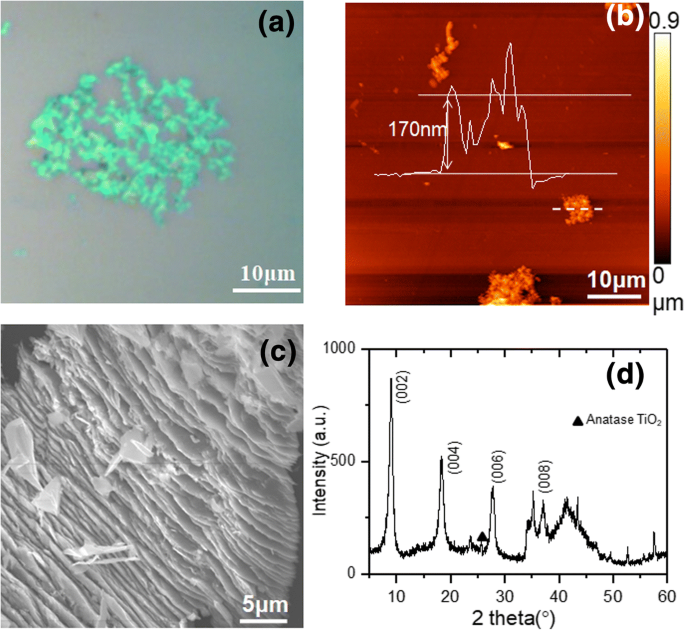
un Imagen óptica de Ti ₃ exfoliado ultrasónicamente C ₂ T _x copos b Imagen topográfica AFM de Ti ₃ exfoliado ultrasónicamente C ₂ T _x escamas, y un perfil de línea a través de la línea punteada marcada se muestra como un recuadro, lo que indica el Ti ₃ C ₂ T _x espesor de las escamas de 170 nm; c Imagen SEM de Ti ₃ exfoliado ultrasónicamente C ₂ T _x copos d Espectros XRD de Ti ₃ C ₂ T _x polvo crudo

Además, medimos los espectros XRD de Ti ₃ en bruto C ₂ T _x polvo, como se muestra en la Fig. 1d. Este patrón XRD es una analogía con informes anteriores [10]; por tanto, los picos prominentes a 8,95 °, 18,28 ° y 27,7 ° pueden asignarse a las difracciones de los planos (002), (004) y (006). En comparación con los picos prominentes, la intensidad de los picos de difracción de las fases menores (anatasa TiO ₂ (101) a 25,3 °, tarjeta JCPDS n. ° 71-1116) es relativamente débil, lo que indica la alta pureza de Ti ₃ C ₂ T _x fase en el polvo obtenido. El pico (002) emerge en un ángulo ligeramente más bajo que el informado por Han et al. (9,21 °) [10]. El c calculado El parámetro de red, 19,66 Å, es mayor que el valor informado (19,2 Å) [10]. Cabe señalar que, dado que el espacio entre capas puede estar sintonizado por diferentes densidades de grupos químicos e iones, como –F, –OH y Li ⁺ , el c El parámetro de la red varía sustancialmente de 19,2 Å a 58,8 Å en diferentes estudios [10, 20, 26, 27]. El c El parámetro de celosía de nuestra muestra está muy cerca del valor bajo que se midió para Ti ₃ C ₂ T _x polvo simplemente usando HF como grabador [10].

Los espectros XRD de Ti ₃ C ₂ T _x las escamas medidas a diferentes presiones hasta 26,7 GPa se muestran en la Fig. 2a. Se puede ver que los espectros medidos a diferentes presiones son similares entre sí, mientras que no se puede encontrar ningún pico de difracción nuevo. Este hallazgo indica que no se produce ninguna transformación de fase con una presión de hasta 26,7 GPa. En la Fig. 2a, todos los picos de difracción cambian a ángulos grandes al aumentar la presión, lo que indica la contracción del Ti ₃ C ₂ T _x enrejado. Esta compresibilidad pseudo-negativa también se ha observado para Ti ₃ C ₂ T _x [20] y otros materiales de baja dimensión con una estructura en capas, como grafito [28], óxido de grafeno [29, 30], MoS ₂ [31], arcilla [32] y titanatos [33]. El pico (002) cambia de 2.883 ° a 3.162 ° a medida que la presión aumenta de 1.8 GPa a 26.7 GPa. La relación de deformación del parámetro de celosía c , c / c ₀ , en función de la presión, se puede calcular a partir del desplazamiento de (002) pico. Además, la relación de deformación de a , a / a ₀ , se puede calcular a partir del desplazamiento de (110) pico. Como se muestra en la Fig. 2b, los parámetros de celosía c y a se deforman un 9,1% y un 2,4%, respectivamente, a una presión de 26,7 GPa. En la región de baja presión a ~ 3 GPa, la relación de compresión del parámetro de celosía c es del 3%. En la anterior medición XRD de alta presión de Ti ₃ C ₂ T _x copos, una c un poco más grande Relación de compresión del 4% para Ti ₃ seco C ₂ T _x copos fue informado por Ghidiu et al. [11] (Figura 2b). Esta diferencia podría ser inducida por un parámetro de celosía más grande c (25,1 Å) de la muestra utilizada por Ghidiu et al. [11] con respecto al nuestro (19,66 Å).

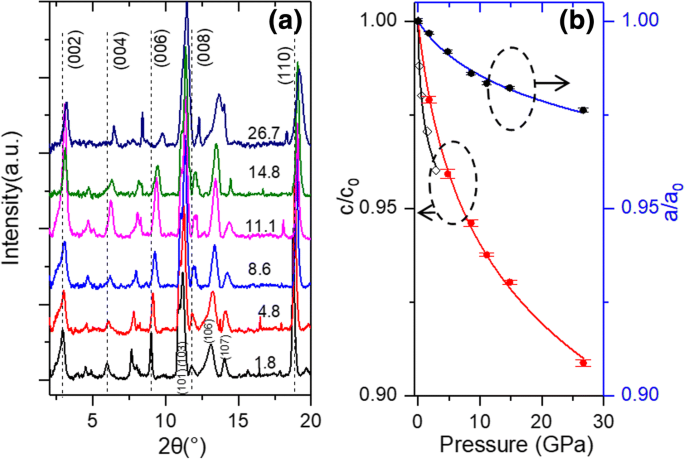
un Espectros XRD de Ti ₃ C ₂ T _x a diferentes presiones cargadas. Tenga en cuenta que la unidad es GPa para la presión anotada en cada espectro. Los picos se asignan de acuerdo con la ref. [26]; b experimental (puntos) y relación de compresión calculada (línea continua) a lo largo de c y a direcciones. Las líneas continuas son los resultados ajustados usando la ecuación \ (r (P) / {r} _0 ={\ left [\ left ({\ delta} _0 / {\ delta} ^ {\ prime} \ right) P + 1 \ right]} ^ {\ delta ^ {\ prime}} \)

Para obtener las constantes elásticas, la c y a Las relaciones de compresión en la Fig. 2b se ajustan aún más utilizando la ecuación de Murnaghan [34].

$$ r (P) / {r} _0 ={\ left [\ left ({\ beta} ^ {\ prime} / {\ beta} _0 \ right) P + 1 \ right]} ^ {- 1 / { \ beta} ^ {\ prime}} $$ (1)

donde r representa las constantes de celosía a lo largo de c y a ejes, \ ({\ beta} _0 ^ {- 1} =- {\ left (\ frac {dlnr} {lnP} \ right)} _ {P =0} \) es la compresibilidad lineal, y β ^′ es la presión derivada de β .

La r ajustada / r ₀ curvas de a y c se trazan como líneas continuas en la Fig. 2b. Puede verse que los resultados experimentales se ajustan muy bien a la expectativa de la ecuación. El mejor ajuste genera β ₀ y β ^′ para c como 67,7 GPa y 25,5, respectivamente. Mientras que para el parámetro de celosía a , β ₀ y β ^′ se calculan en 387,4 GPa y 72,1, respectivamente (Tabla 1). Para materiales 2D ultrafinos como el grafeno, el módulo de Young (1TPa) está muy cerca del β ₀ de grafito grueso [19, 28]. Por lo tanto, β ₀ se puede utilizar como sustitución para evaluar la constante elástica de Ti ₃ C ₂ T _x . Módulo de Young de Ti ₃ C ₂ T _x fue medido recientemente por Lipatov et al. 330 GPa [18], lo que es coherente con el β ₀ en nuestro estudio. Nuestros valores medidos también son comparables a las constantes elásticas de Ti ₃ C ₂ que se calcularon en otros estudios [15, 17] (Tabla 1). El β ₀ en c El eje es más grande que el del grafito ( β ₀ = 35,7 GPa), mientras que β ₀ en a El eje es más pequeño que el del grafito ( β ₀ = 1250 GPa) [28]. El β ₀ de Ti ₃ C ₂ T _x es mayor que el módulo de volumen de MoS ₂ (270 Pa) [35] y también es comparable a la del óxido de grafeno (210 GPa) [36], lo que indica una alta constante elástica de Ti ₃ C ₂ T _x Mxene entre materiales 2D.

Espectros Raman de alta presión de Ti ₃ C ₂ T _x Las muestras se midieron a diferentes presiones de compresión de hasta 25,5 GPa, como se muestra en la Fig. 3a. Los espectros Raman obtenidos a diferentes presiones descompresivas se muestran en la Fig. 3b. A bajas presiones de compresión, Ti ₃ C ₂ T _x Mxene exhibe tres bandas Raman principales a ~ 210, ~ 500 y 700 cm ⁻¹ . Cabe señalar que los espectros Raman de Ti ₃ C ₂ T _x MXene varía significativamente en diferentes tipos de literatura. Hu y col. [23] informó fuertes picos Raman a ~ 200 cm ⁻¹ y 720 cm ⁻¹ , mientras que otras bandas a 400 cm ⁻¹ eran bastante amplios. Sin embargo, Han et al. [10] y Zhu et al. [37] observó un pico agudo a ~ 200 cm ⁻¹ , pero otras bandas eran todas amplias. Xue y col. [14] solo observó picos anchos de 100 a 700 cm ⁻¹ . Los espectros Raman en la Fig. 3 son diferentes a los de la ref. [10, 14, 23, 37]. Esta diferencia podría ser inducida por diferentes tipos y concentraciones de grupos químicos en Ti ₃ C ₂ T _x MXene. La interpretación adicional de estas diferentes bandas Raman necesita recordar la dispersión de fonones de Ti ₃ C ₂ T _x que fue calculado teóricamente por Hu et al. [23, 24]. El grupo espacial de Ti ₃ C ₂ T _x era P6 ₃ / mmc [23]. El número de átomos ( N ) en una celda primitiva de Ti ₃ C ₂ T _x se calculó que era 7, 7 y 9 para T =−O, −F y −OH, respectivamente, dado x =2. En Γ punto de la primera zona de Brillouin, se prevé que existan los siguientes fonones ópticos para diferentes Ti ₃ C ₂ T _x MXenes: Γ _óptico (Ti ₃ C ₂ O ₂ ) =6 E _g + 3 A _1g , Γ _óptico (Ti ₃ C ₂ F ₂ , Ti ₃ C ₂ (OH) ₂ ) =8 E _g + 4 A _1g [23]. Las vibraciones del átomo de diferentes modos activos Raman de Ti ₃ C ₂ F ₂ y Ti ₃ C ₂ (OH) ₂ se ilustran esquemáticamente en la Tabla 2. Sus frecuencias fueron calculadas teóricamente por Hu et al. [23] y se enumeran en la Tabla 2. Para Ti ₃ C ₂ (OH) ₂ , hay cuatro modos fuera del plano ( A _1g :218, 514, 684 y 3734 cm ⁻¹ ) y cuatro modos en el plano ( E _g :138, 278, 437 y 622 cm ⁻¹ ). Para Ti ₃ C ₂ F ₂ , hay tres A _1g modos (190, 465 y 694 cm ^{- 1} ) y tres E _g modos (128, 231 y 612 cm ^{- 1} ) [23].

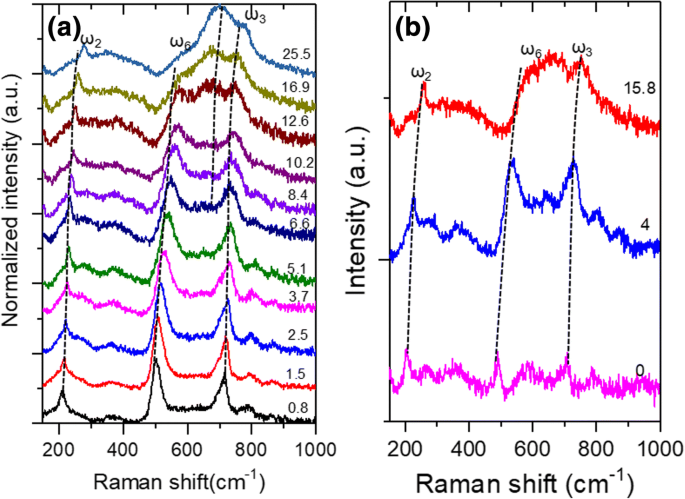
un Espectros Raman de Ti ₃ C ₂ T _x escamas a diferentes presiones de compresión; b Espectros Raman obtenidos a diferentes presiones de descompresión. Tenga en cuenta que la unidad de presiones en a y b es GPa

Sin embargo, se pueden ver las frecuencias fonéticas calculadas de Ti ₃ puro C ₂ F ₂ o Ti ₃ C ₂ (OH) ₂ no se ajusta a los espectros Raman experimentales de Ti ₃ C ₂ T _x en la Fig. 3. Debido a que la superficie de Ti ₃ C ₂ T _x generalmente está unido por un tipo diferente de grupos químicos, una interpretación completa de los espectros experimentales Raman en la Fig. 3 necesita considerar los modos de vibración hibridados de −F y −OH [23]. En una investigación anterior [23], las bandas Raman en ~ 200, ~ 500 y ~ 700 cm ⁻¹ fueron asignados a ω ₂ , ω ₆ y ω ₃ , respectivamente. Siguiendo esta instrucción, las bandas Raman prominentes en 205,6, 490,2 y 702,5 cm ⁻¹ de la Fig. 3a, b se puede asignar a ω ₂ , ω ₆ y ω ₃ modos, respectivamente. Curiosamente, estos modos son todos modos fuera del plano. Otros modos Raman son difíciles de aislar de sus modos vecinos debido a sus bajas intensidades. Para obtener datos sólidos al eliminar las incertidumbres, solo estos tres modos se consideran en los siguientes cálculos y análisis.

En las Fig. 3a, b, también se puede ver que las intensidades relativas de estos modos en el plano aumentan con las presiones de compresión crecientes (Fig. 3a). Cuando la presión de compresión es ≥ 12,6 GPa, un nuevo pico a ~ 600 cm ⁻¹ (ω ₄ ) emerge y se convierte en el pico prominente. En el proceso de descompresión, las intensidades de este ω ₄ modo disminuyen significativamente. Los espectros Raman obtenidos a 0 GPa de presión de descompresión contienen casi todos los modos de fonones en el plano y fuera del plano. Tal aparición de modos en el plano a alta presión de compresión podría estar relacionada con la fractura de escamas o la polarización inducida por rotación de orientación. La investigación sobre este efecto aún está en curso y se informará en el futuro.

Al aumentar la presión de 0,8 GPa a 25,6 GPa, ω ₂ , ω ₆ y ω ₃ todos muestran desplazamientos al azul monótonos en aumento (Fig. 4a-d), que son similares a los desplazamientos al azul dependientes de la presión del grafito [28] y MoS ₂ [31]. A 25,6 GPa, los desplazamientos al azul de estos tres modos son 66,7, 85,1 y 60 cm ⁻¹ , respectivamente. Tales cambios al azul dependientes de la presión son mucho mayores que los de MoS ₂ [31]. Para cuantificar el cambio Raman frente a la presión, los gráficos de cambio Raman de la Fig. 4a, b, d se ajustaron utilizando la siguiente ecuación [28]:

$$ \ omega (P) / {\ omega} _0 ={\ left [\ left ({\ delta} _0 / {\ delta} ^ {\ prime} \ right) P + 1 \ right]} ^ {\ delta ^ {\ prime}} $$ (2)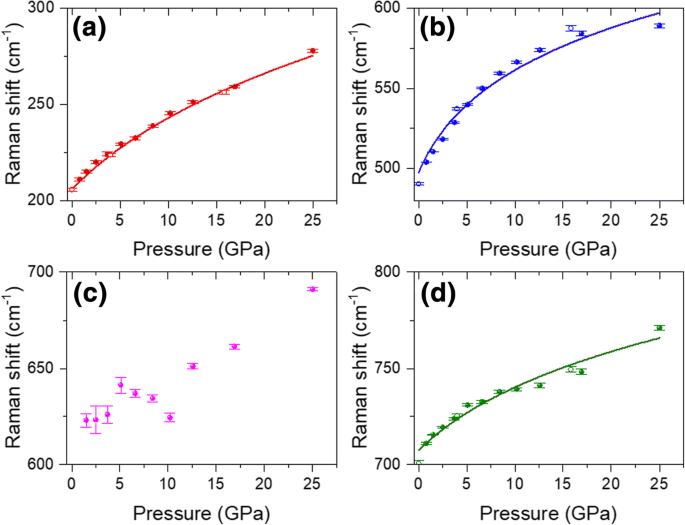

Cambios Raman de diferentes modos de fonón en función de diferentes presiones de compresión (esfera sólida) y presiones de descompresión (círculos abiertos): a 210 cm ⁻¹ , b 504 cm ⁻¹ , c 620 cm ⁻¹ y d 711 cm ⁻¹ . Las líneas continuas son los resultados del ajuste usando la ecuación \ (\ omega (P) / {\ omega} _0 ={\ left [\ left ({\ delta} _0 / {\ delta} ^ {\ prime} \ right) P + 1 \ right]} ^ {\ delta ^ {\ prime}} \)

donde δ ₀ y δ ^′ son la derivada logarítmica de la presión ( dlnω / dP ) _{P =0} y la derivada de presión de dlnω / dP , respectivamente. Los resultados ajustados se representan como líneas continuas en la Fig. 4a, b, d. Debido a las altas incertidumbres en la región de baja presión, el modo Raman a 620 cm ⁻¹ no estaba ajustado. Puede verse en las Fig. 4a, b, d que las curvas ajustadas son consistentes con los resultados experimentales, lo que indica la alta precisión del proceso de ajuste. Los parámetros obtenidos de δ ₀ y δ ^′ se enumeran en la Tabla 3.

Para materiales 2D anisotrópicos con un espesor atómico, como MXene y grafeno, dos componentes independientes de los tensores de Grüneisen suelen estar asociados con las deformaciones que son paralelas y perpendiculares a la c eje. Para simplificar, adoptamos la relación de escala propuesta por Zallen et al. [38], que se ha utilizado para ajustar el cambio Raman dependiente de la presión del grafito por Hanfland et al. [28]

$$ \ omega (P) / {\ omega} _0 ={\ left [r (P) / {r} _0 \ right]} ^ {3 \ gamma} $$ (3)

donde r se refiere a las constantes de celosía en el plano y fuera del plano para los modos intracapa e intercapa, respectivamente. γ es equivalente al parámetro de Grüneisen que se definió en otros estudios [39, 40].

Como solo se observan los modos fuera del plano en el proceso de compresión, c El parámetro de celosía en función de la presión hidrostática es adecuado para el cálculo. Adoptamos los datos de distancia espacial del plano (002) de 0 a 26,7 GPa en la Fig. 2b para el cálculo del parámetro de Grüneisen γ . El \ (\ overline {\ upgamma} \) promediado hasta 26,7 GPa para ω ₂ , ω ₆ y ω ₃ se calcularon en 1,08, 1,16 y 0,29, respectivamente (Tabla 2). Similar al grafito, el \ (\ overline {\ upgamma} \) más pequeño de ω ₃ en comparación con los otros dos modos, indica que hay un cambio menor en las constantes de fuerza involucradas en el movimiento de la capa rígida [28]. Hasta donde sabemos, los parámetros Grüneisen de Ti ₃ C ₂ T _x aún no han sido reportados. Sin embargo, aún podemos comparar nuestros datos con otros materiales 2D. Zha y col. informaron los parámetros de Grüneisen como 4-5 para los modos de fonón acústico de Ti ₂ CO ₂ [41]. Debido a que los parámetros de Grüneisen de los modos ópticos de alta frecuencia suelen ser uno o dos órdenes más bajos que los de los modos de baja frecuencia [28], los parámetros de Grüneisen para fonones ópticos de Ti ₂ CO ₂ se puede estimar en 0.05–0.5, que son similares a los de nuestros valores para Ti ₃ C ₂ T _x . Recientemente, Peng et al. [42] informó que los parámetros de Grüneisen a temperatura ambiente eran 1,22, 1,20 y 1,15 para MoS ₂ , MoSe ₂ y WS ₂ , respectivamente, que son mayores que nuestros resultados. Nuestros resultados también son más pequeños que los del grafeno (1,99 para E _2g modo) [40] y grafito (1.06 para E _2g modo) [28]. Este hallazgo indica que Ti ₃ C ₂ T _x MXene tiene la anarmonicidad de unión más débil entre estos materiales 2D ultradelgados [42].

Conclusiones

En conclusión, medimos la deformación de la red y la respuesta fonética de Ti ₃ C ₂ T _x escamas delgadas a diferentes presiones hidrostáticas hasta 26,7 GPa. No se ha observado transformación de fase por debajo de una presión de 26,7 GPa. Todos los modos de fonón muestran un cambio de frecuencia positivo con presiones crecientes. Los parámetros positivos de Grüneisen de tres fonones fuera del plano se calculan en 1,08, 1,16 y 0,29. Nuestros resultados aumentan la comprensión de las propiedades mecánicas y térmicas del Ti ₃ C ₂ T _x a altas presiones.

Métodos

Ti ₃ C ₂ T _x El polvo se preparó mediante un método indicado en la referencia [43]. Brevemente, Ti ₃ AlC ₂ El polvo (Forsman, 10 g) se atacó con una solución de HF (160 ml) a temperatura ambiente durante 5 h. El Ti ₃ obtenido C ₂ T _x el polvo se dispersó en agua desionizada y se exfolió ultrasónicamente a una potencia de 700 W. La solución resultante se separó después de almacenarse durante 24 h. La solución de la capa superior obtenida se utilizó para análisis adicionales de Raman, microscopio de fuerza atómica (AFM) y microscopio electrónico de barrido (SEM). Los espectros de difracción de rayos X (XRD) a presión ambiental se midieron usando un difractómetro de rayos X (Rigaku, MiniFlex600). Las imágenes SEM se obtuvieron utilizando un microscopio electrónico de barrido (Hitachi, Su1510). Se realizaron mediciones de XRD de alta presión in situ en la Instalación de Radiación del Sincrotrón de Shanghai mediante una celda de yunque de diamante de alta presión (DAC) con junta a temperatura ambiente. Para producir un ambiente hidrostático alrededor de la muestra, usamos metanol / etanol / agua (16:3:1) como medio transmisor de presión. La presión se determinó mediante el desplazamiento espectral dependiente de la presión de la línea R1 de fluorescencia rubí nítida. La muestra se colocó en un orificio de junta de acero inoxidable (100 µm de diámetro) con un culet de diamante (400 µm de diámetro). Se realizaron mediciones de dispersión Raman a alta presión utilizando un espectrómetro Renishaw inVia Raman con una longitud de onda de excitación de 532 nm. Las mediciones topográficas se realizaron en un instrumento AFM (Bruker, Innova).

El ajuste de las posiciones de los picos de difracción y los cambios de los picos Raman se realizó en el paquete OriginPro. Una función definida por el usuario, y =(A1 × x + 1) ^A2 , se utilizó estableciendo A1 y A2 como parámetros de ajuste. El ajuste adecuado se puede obtener fácilmente mediante un método simplex.

Abreviaturas

2D:

Dos dimensiones

AFM:

Microscopio de fuerza atómica

DAC:

Celda de yunque de diamante

SEM:

Microscopio electrónico de barrido

TMD:

Dicalcogenuros de metales de transición

XRD:

Difracción de rayos X

Preparación y propiedades electroquímicas de los ánodos de Fe2O3 / C en forma de granada para baterías de iones de litio Diseño racional de arquitectura porosa hueca de Ni (OH) 2 para sensor de glucosa sin enzimas de alta sensibilidad