Estudio de termometría en Sb2Te3 bidimensional a partir de espectroscopia Raman dependiente de la temperatura

Resumen

El descubrimiento de aisladores topológicos (TI) bidimensionales (2D) demuestra un enorme potencial en el campo de la termoeléctrica desde la última década. Aquí, hemos sintetizado 2D TI, Sb ₂ Te ₃ de varios espesores en el rango de 65-400 nm usando exfoliación mecánica y coeficiente de temperatura estudiado en el rango de 100-300 K usando espectroscopía micro-Raman. Se ha analizado la dependencia de la temperatura de la posición del pico y el ancho de línea de los modos de fonón para determinar el coeficiente de temperatura, que se encuentra en el orden de 10 ^–2 cm ⁻¹ / K, y disminuye con una disminución en Sb ₂ Te ₃ grosor. Tal coeficiente de baja temperatura favorecería lograr una alta figura de mérito ( ZT ) y allanar el camino para utilizar este material como un excelente candidato para materiales termoeléctricos. Hemos estimado la conductividad térmica de Sb ₂ Te ₃ escamas con un grosor de 115 nm soportadas en SiO ₂ de 300 nm / Sustrato de Si que se encuentra en ~ 10 W / m – K. El valor de conductividad térmica ligeramente más alto sugiere que el sustrato de soporte afecta significativamente la disipación de calor del Sb ₂ Te ₃ escamas.

Introducción

Los aislantes topológicos (TI) son la nueva clase de materiales cuánticos que tienen una amplia brecha de energía en el volumen y en la superficie menos estados similares a Dirac, que están protegidos bajo simetría de inversión del tiempo [1, 2, 3]. Estos materiales son muy prometedores para una amplia gama de aplicaciones potenciales, incluidos transistores de efecto de campo [4, 5], detectores infrarrojos de THz [6], sensores de campo magnético [7, 8] y termoelectricidad [9, 10]. El rendimiento termoeléctrico de cualquier material a una temperatura T se rige por la figura adimensional del mérito ZT ( ZT = S ² σT / κ , donde S , σ y κ denotan el coeficiente de Seebeck, la conductividad eléctrica y la conductividad térmica, respectivamente [11, 12]. Se ha demostrado que la dimensionalidad reducida de estos materiales es uno de los enfoques más comunes para minimizar la conductividad térmica y obtener un ZT alto. [13]. Para minimizar la conductividad térmica, es muy importante comprender la dinámica de los fonones en este tipo de material, particularmente las interacciones fonón-fonón y electrón-fonón, todas las cuales tienen un gran impacto en el rendimiento del dispositivo termoeléctrico [14, 15].

Se ha demostrado que la dispersión Raman es una herramienta importante para probar los modos vibracionales en un material basándose en su naturaleza microscópica y no destructiva [16, 17]. También proporciona información importante sobre el dopaje, la ingeniería de deformaciones y las fases cristalinas [18, 19]. Si bien las caracterizaciones Raman a temperatura ambiente de los modos de fonón en varios TI 2D se han estudiado bien en la literatura [20, 21], las caracterizaciones Raman de la dependencia de la temperatura aún se encuentran en una etapa incipiente. Además, es bien sabido que el cambio de temperatura puede variar las distancias interatómicas y afectar varios modos de fonón en el cristal [14]. Por lo tanto, los espectros Raman dependientes de la temperatura son muy adecuados para obtener información sobre la conductividad térmica de los materiales, así como los efectos isotópicos y la vida útil de los fonones [22, 23].

En este trabajo, presentamos espectroscopía Raman dependiente de la potencia a temperatura ambiente y espectroscopía Raman dependiente de la temperatura en el rango de temperatura entre 100 y 300 K de 2D Sb ₂ Te ₃ cristales de varios espesores. La variación de la posición del pico Raman y el ancho completo a la mitad del máximo ( FWHM ) con respecto a la temperatura y la potencia, y los resultados se interpretan para determinar el coeficiente de expansión térmica y la conductividad térmica de Sb ₂ Te ₃ escamas en el contexto del estudio de termometría. El valor de la conductividad térmica para Sb ₂ Te ₃ Se ha estimado la escama con un espesor de 115 nm y se ha discutido el papel del sustrato para mejorar la conductividad térmica.

Métodos

La exfoliación mecánica se llevó a cabo en Sb ₂ a granel de alta calidad Te ₃ crystal (2D Semiconductors, EE. UU.) utilizando la técnica estándar de cinta adhesiva [24] para obtener Sb ₂ Te ₃ escamas de diferentes espesores (65 nm, 80 nm, 115 nm, 200 nm y 400 nm) en SiO ₂ de 300 nm / Sustratos de Si. Las muestras exfoliadas se identificaron con la ayuda de un microscopio óptico (LV100ND-Nikon Microscope). Los tamaños laterales del Sb ₂ Te ₃ nanoflakes se encuentran en el rango de 5-7 μm. Se utilizó Park NX-10 AFM (microscopía de fuerza atómica) para medir el grosor del Sb ₂ Te ₃ escamas usando el modo sin contacto.

Los espectros Raman se midieron en varias escamas usando un sistema micro-Raman confocal HORIBA LabRAM en una geometría de retrodispersión usando una excitación láser de 632 nm. Se utilizó como fuente de excitación un láser con un tamaño de punto de ~ 1 µm y una potencia óptica sintonizable de ~ 0,4 a 2,6 mW. Los espectros se recogieron usando un espectrómetro equipado con una cámara CCD enfriada con nitrógeno líquido. Los espectros se adquirieron en el rango de frecuencia de 100 a 200 cm ⁻¹ con una resolución espectral de 1 cm ⁻¹ . Todas las medidas se tomaron utilizando un tiempo de integración de 10 s, adquisiciones de 10 y rejilla de 1800. Para las mediciones de temperatura ambiente (RT), se utilizó un objetivo de 100 ×, mientras que el objetivo de 50 × de larga distancia de trabajo se utilizó para las mediciones de baja temperatura.

Resultados y discusión

Sb ₂ Te ₃ es un TI, que cristaliza en la estructura cristalina romboédrica con el grupo espacial D ⁵ _{3 d} (\ (R \ overline {3} m \)), y su celda unitaria contiene cinco átomos [20]. Este cristal se forma apilando capas de cinco átomos a lo largo de la z- dirección, que se conoce como una capa quíntuple (QL) como se muestra en la Fig. 1, con un espesor de aproximadamente 0,96 nm [20]. Desde el registro atómico, podemos ver que el átomo de Sb está intercalado entre dos átomos de Te, con el Te ⁽²⁾ átomo que actúa como centro de inversión. Esta propiedad centrosimétrica de la estructura cristalina da lugar a modos activos Raman mutuamente independientes. Los átomos dentro de un solo QL se mantienen unidos por fuertes fuerzas covalentes, mientras que la fuerza entre QL es mucho más débil y del tipo de van der Waal. Debido a la fuerza de van der Waal débil en la dirección fuera del plano, es posible exfoliar mecánicamente capas delgadas de este material de sus cristales a granel. Aunque las muestras exfoliadas conservan la composición y estructura de los cristales a granel, hay un cambio en la dinámica de los fonones cuando su espesor se reduce al nivel de nanoescala [25, 26].

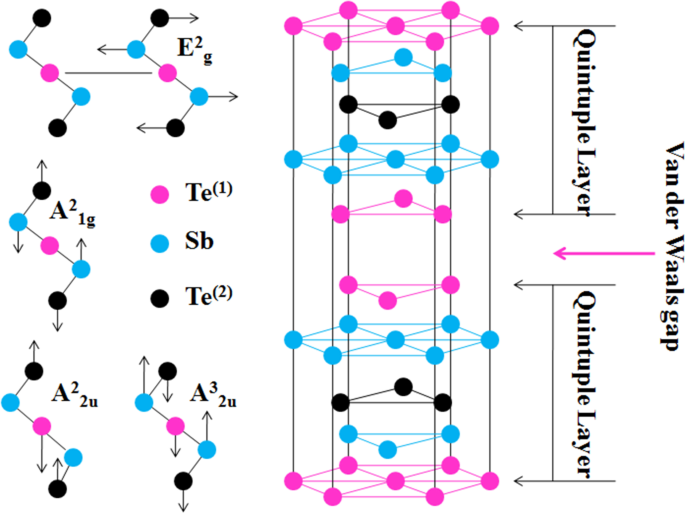
Esquema de Sb ₂ Te ₃ cristal que muestra la disposición de los átomos y la brecha de van der Waals. Los círculos rosa, azul claro y negro representan el Te ⁽¹⁾ , Sb y Te ⁽²⁾ átomos, respectivamente. El panel de la izquierda muestra los posibles modos de teléfono en el rango de frecuencia de 100 cm ⁻¹ hasta 200 cm ⁻¹ . Las flechas representan la dirección de las vibraciones de los átomos constituyentes

Imágenes de micrografía óptica (OM) de tres Sb ₂ diferentes Te ₃ nanoflakes exfoliados en SiO ₂ / El sustrato de Si se muestra en la Fig. 2a-c. Los tamaños laterales de las escamas están en el rango de 5-7 μm, que son lo suficientemente grandes para ser observados en MO. Se puede observar que el contraste de color de las escamas es muy sensible al grosor de las escamas es decir, diferentes espesores muestran diferentes contrastes de color. Los espesores de estas escamas preparadas se midieron mediante microscopía de fuerza atómica (AFM), que se muestran en el panel inferior de la Fig. 2 junto con sus perfiles de altura de sección transversal (Fig. 2d-f). Los valores de espesor de estas escamas se estimaron en 65 nm, 115 nm y 200 nm y se encontró que eran casi uniformes excepto por algunas protuberancias. Pero, todas las medidas Raman se tomaron en la posición de las escamas, donde se mantuvo la uniformidad.

a-c Imágenes OM de Sb ₂ Te ₃ escamas de espesores de 65 nm, 115 nm y 200 nm, respectivamente. d-f Sus imágenes AFM representativas y perfiles de altura.

La Figura 3 presenta los espectros Raman dependientes de la energía de los tres copos anteriores medidos a temperatura ambiente, que consta de cuatro modos vibratorios que incluyen dos modos activos Raman E ² _g y A ² _1g asignado a frecuencias ~ 125 cm ⁻¹ y ~ 169 cm ⁻¹ y dos modos activos de infrarrojos A ² _2u y A ³ _2u asignado a ~ 115 cm ⁻¹ y ~ 144 cm ⁻¹ , respectivamente [20, 27]. Se observa claramente que hay un corrimiento hacia el rojo así como un aumento en la intensidad máxima de todos los modos Raman con un aumento en la potencia del láser para todas las escamas (65 nm, 115 nm y 200 nm). Estos cambios sugieren que el aumento de la potencia del láser conduce a un aumento considerable de la temperatura local en la superficie de la muestra [28]. Sb ₂ Te ₃ las escamas con espesores de 115 nm y 200 nm exhiben los cuatro modos (A ² _2u , E ² _g , A ³ _2u y A ² _1g ) para una potencia láser baja de 0,402 mW y A ² _2u y E ² _g los modos se combinan con un mayor aumento de potencia, que se puede ver en el ancho de línea asimétrico de A ² _2u / E ² _g modos en la Fig. 3b, c. La Figura 3a muestra los espectros Raman de Sb ₂ Te ₃ escamas con un grosor de 65 nm a tres potencias de láser incidentes diferentes, y todo el espectro muestra solo dos modos Raman E ² _g y A ³ _2u a temperatura ambiente. En este caso, la forma de E ² _g picos para todos los poderes del láser parece asimetría, lo que implica que también hay fusión de ambos A ² _2u y E ² _g modos similares a escamas gruesas (115 nm, 200 nm) a alta potencia láser. Sin embargo, el A ² _1g está completamente ausente para este espesor. Creemos que este modo serían las características de la vibración fuera del plano, que no sería tan significativa para este espesor.

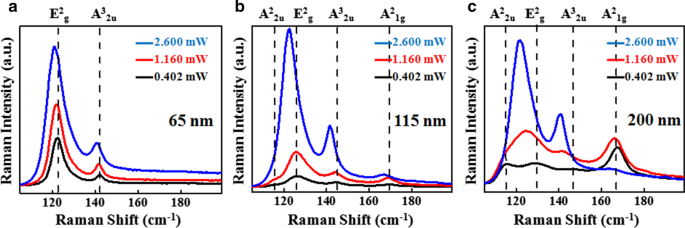
a-c Espectros micro-Raman dependientes de la potencia de 65 nm, 115 nm y 200 nm Sb ₂ Te ₃ copos, respectivamente. Los espectros se miden utilizando láser de 632 nm con tres potencias diferentes:0,402 mW, 1,160 mW y 2,600 mW. Las líneas discontinuas muestran la posición de los modos Raman.

La comparación de espectros Raman de tres muestras de diferentes espesores (65 nm, 115 nm y 200 nm) a una potencia láser particular de 0,402 mW se presenta en la Fig. 4a. Todos los modos Raman observados y sus asignaciones se enumeran en la Tabla 1. Es muy interesante observar que A ² _1g y A ² _2u Los modos para escamas de 200 nm poseen más intensidad que los otros dos modos (E ² _g y A ³ _2u ). A ² _1g y A ² _2u Los modos son más sensibles al espesor porque refleja las vibraciones fuera del plano y las interacciones de van der Walls entre capas. En el caso de Sb ₂ Te ₃ escamas con un grosor de 65 nm y 115 nm, la forma de E ² _g picos para todos los poderes del láser parece asimetría, lo que implica que hay una fusión de ambos A ² _2u y E ² _g modos. Sin embargo, el A ² _1g está completamente ausente para Sb ₂ Te ₃ escamas con un espesor de 65 nm. Este modo Raman en particular se originaría debido a una vibración fuera del plano, que podría no responder a este grosor. Se observa un desplazamiento hacia el rojo para E ² _g y A ³ _2u modos de fonón en el caso de escamas más delgadas, similar a lo informado por Zang et al. [30], mientras que A ² _1g El modo muestra un cambio ligeramente azul (ver Tabla 1). Las intensidades máximas de 65 nm Sb ₂ Te ₃ las escamas son más pronunciadas que las más gruesas bajo la misma potencia del láser de excitación, y este fenómeno se puede atribuir a las mejoras de interferencia óptica que se producen tanto para el láser de excitación como para la radiación Raman emitida en la capa de TI / SiO ₂ / Si system [30], que también se informa para Bi ₂ Se ₃ y Bi ₂ Te ₃ [26, 31]. A partir de los espectros Raman dependientes de la potencia de 115 nm Sb ₂ Te ₃ escamas (Fig. 3b), las frecuencias Raman de E ² _g &A ² _1g Los modos se han extraído en función de la potencia del láser, como se muestra en la Fig. 4b. El cambio en la frecuencia del fonón con el cambio en la potencia del láser incidente es decir, coeficiente de potencia ( δω / δP ) se ha estimado a partir del ajuste lineal de los datos extraídos, que se encuentra en - 1,59 cm ⁻¹ / mW y - 1,32 cm ⁻¹ / mW correspondiente a E ² _g y A ² _1g modos.

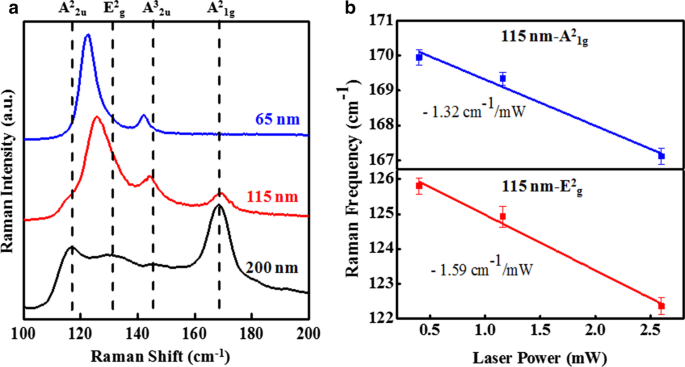
un Comparación de espectros micro-Raman dependientes del espesor de 65 nm, 115 nm y 200 nm Sb ₂ Te ₃ copos a una potencia de láser de 0,402 mW. Las líneas discontinuas muestran la posición de los modos Raman. b Gráficos de frecuencia Raman frente a potencia láser de E ² _g &A ² _1g modos para 115 nm Sb ₂ Te ₃ escama. Las líneas continuas son los ajustes lineales a los datos experimentales (símbolos). Las pendientes calculadas a partir de los ajustes lineales se muestran como recuadros. La incertidumbre en la medición de la frecuencia Raman se ha mostrado como barras de error

Los espectros Raman dependientes de la temperatura se midieron en el rango de temperatura de 100 a 300 K como se muestra en la Fig. 5 para tres escamas diferentes con espesores de 80 nm, 115 nm y 400 nm, respectivamente, a una potencia de láser de 1,16 mW. Las imágenes de OM, AFM junto con perfiles de altura de 80 nm y 400 nm exfoliaron Sb ₂ Te ₃ las escamas se dan en el archivo adicional 1:información de apoyo S1. A la temperatura más baja de 100 K, cuatro modos Raman de características (A ² _2u , E ² _g , A ² _1g y A ³ _2u ) de Sb ₂ Te ₃ son claramente distinguibles, mientras que A ² _2u y E ² _g Los modos Raman se fusionan hacia temperaturas más altas es decir, 220 K y 300 K. Se observaron corrimientos al rojo y ensanchamiento de picos en todos los modos Raman (A ² _2u , E ² _g , A ² _1g y A ³ _2u ) con el aumento de temperatura de 100 a 300 K. En general, la espectroscopia Raman dependiente de la temperatura se usa ampliamente para investigar la expansión térmica, la conducción térmica y el acoplamiento entre capas [15, 31, 32]. Además, la frecuencia pico tiene una dependencia lineal con la temperatura, que viene dada por [15],

$$ \ omega \ left (T \ right) =\ omega_ {0} + \ chi T $$ (1)

donde ω ₀ es la frecuencia de vibración de estos modos de fonón a temperatura de cero absoluto, y χ es el coeficiente de temperatura de primer orden de estos modos de fonón. Se ha informado que la expansión y contracción térmica de los modos de cristal y fonón puede llevar a la dependencia de la posición del pico en la espectroscopía Raman con la temperatura [33].

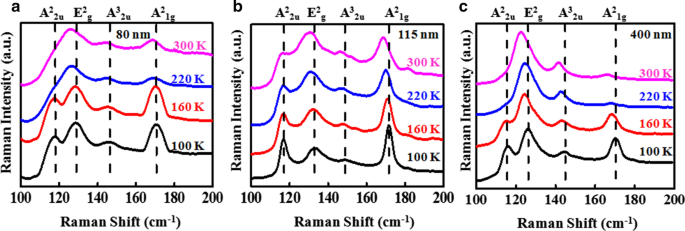
a-c Espectros micro-Raman dependientes de la temperatura de Sb ₂ Te ₃ de espesor 80 nm, 115 nm y 400 nm, respectivamente. Las curvas de color negro, rojo, azul y azul claro representan los espectros Raman a 100 K, 160 K, 220 K y 300 K, respectivamente, para una potencia de láser de 1,16 mW. Las líneas discontinuas muestran la posición de los modos Raman.

Las gráficas de posición pico versus temperatura de E ² _g &A ² _1g los modos se muestran en la Fig. 6a, b, respectivamente, para muestras de diferentes espesores. Las gráficas de posición de pico versus temperatura (Fig. 6a, b) se han ajustado linealmente usando la Ec. 1 para calcular el coeficiente de temperatura de primer orden ( χ ) y los valores del coeficiente de temperatura de primer orden para E ² _g &A ² _1g Los modos Raman se enumeran en la Tabla 2. La ampliación en FWHM de E ² _g &A ² _1g Los modos Raman con aumento de temperatura se muestran en la Fig. 7a, b, respectivamente. La dependencia de la temperatura del FWHM es una medida de anarmonicidad fonónica y aumenta linealmente con el aumento de temperatura. La aproximación anarmónica más simple, conocida como el modelo de acoplamiento simétrico de tres fonones [34], tiene en cuenta la desintegración del fonón óptico en dos fonones con energías iguales y momentos opuestos. En el presente trabajo, hemos calculado el coeficiente de temperatura de primer orden ( χ) y conductividad térmica de los espectros Raman dependientes de la temperatura. Sin embargo, no estamos analizando el FWHM en el contexto de ZT ya que no tiene una relevancia tan directa.

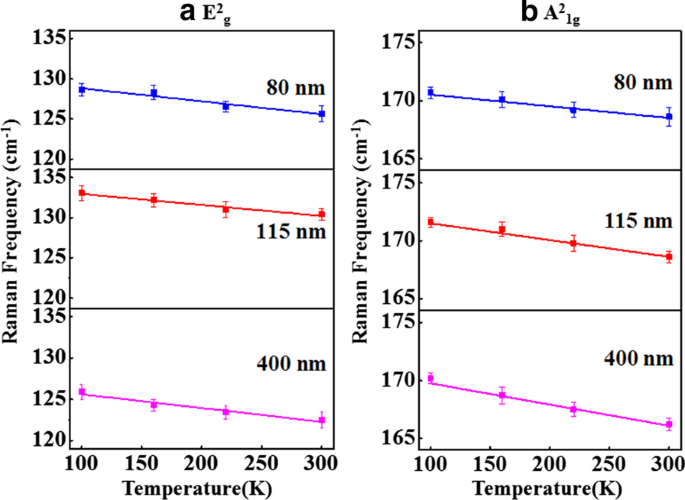
Gráficos de frecuencia Raman frente a temperatura de a E ² _g modo y b A ² _1g modo para 80 nm, 115 nm y 400 nm Sb ₂ Te ₃ copos. Las líneas continuas son los ajustes lineales a los datos experimentales (símbolos). La incertidumbre en la medición de la frecuencia Raman se ha mostrado como barras de error

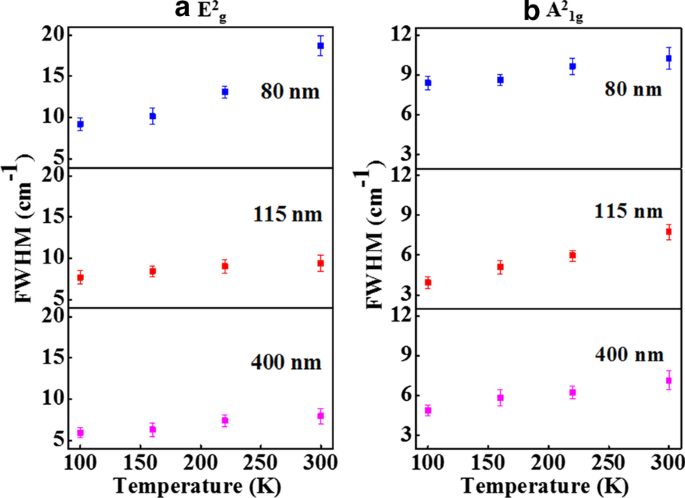
Gráficos de FWHM frente a temperatura de a E ² _g modo y b A ² _1g modo para 80 nm, 115 nm y 400 nm Sb ₂ Te ₃ copos. La incertidumbre en la estimación FWHM se ha mostrado como barras de error

Se observa que el valor de los coeficientes de temperatura de primer orden ( χ ) para E ² _g y A ² _1g el modo es del orden de 10 ^–2 cm ⁻¹ / K. El valor de χ correspondiente a A ² _1g el modo disminuye de - 2 × 10 ^–2 a - 1 × 10 ^–2 cm ⁻¹ / K cuando el grosor de Sb ₂ Te ₃ la escama se reduce de 400 a 80 nm. Tan bajo χ daría baja conductividad térmica y favorecería obtener una alta figura de mérito ( ZT ). Sin embargo, el valor de χ correspondiente a E ² _g el modo es casi constante e independiente del espesor. Ahora, hemos calculado un valor aproximado de conductividad térmica de Sb ₂ Te ₃ escamas utilizando los valores del coeficiente de potencia y del coeficiente de temperatura de primer orden. La conducción de calor a través de una superficie con el área de la sección transversal S se puede evaluar a partir de la siguiente ecuación:\ (\ Partical Q / \ Partical t =- \ kappa {\ oint} \ nabla T.dS, \) donde Q es la cantidad de calor transferida durante el tiempo t y T es la temperatura absoluta. Considerando el flujo de calor radial, Balandin et al . [40] han obtenido una expresión para la conductividad térmica del grafeno, que viene dada por

$$ =\ left ({1/2 \ pi h} \ right) \ left ({\ Delta P / \ Delta T} \ right) $$ (2)

donde h es el espesor de la película 2D del material y el aumento de temperatura local ΔT se debe al cambio en la potencia de calefacción ΔP . Al diferenciar la ecuación. (1) con respecto a la potencia y la sustitución ( ΔP / ΔT ) en la expresión (2), la conductividad térmica se puede escribir de la siguiente manera,

$$ =\ chi \ left ({\ frac {1} {2 \ pi h}} \ right) \ left ({\ frac {\ delta \ omega} {{\ delta P}}} \ right) ^ {- 1} $$ (3)

donde κ es conductividad térmica, h es el grosor de la película 2D del material, χ es el coeficiente de temperatura de primer orden, y ( δω / δP ) es un cambio en la frecuencia del fonón con un cambio en la potencia del láser incidente es decir, coeficiente de potencia de determinados modos Raman. Se encuentra que la conductividad térmica calculada es ~ 10 W / m – K para Sb ₂ Te ₃ escamas con un grosor de 115 nm soportadas en SiO ₂ de 300 nm / Sustrato de Si. Este valor es relativamente más alto que la conductividad térmica informada de otros TI [41]. La ligera mejora en la conductividad térmica sugiere que el sustrato de soporte juega un papel más sensible es decir, el valor de la conductividad térmica puede depender de las cargas interfaciales [42]. Esta mayor conductividad térmica en la muestra soportada por el sustrato también puede explicar el menor aumento de temperatura bajo alta potencia del láser en comparación con la muestra suspendida. El efecto de sustrato similar también se informa en Su et al . para capas de fósforo negro [42]. Guo y otros . También informó que, en ciertas regiones, el efecto de la dispersión de fonones puede suprimirse y la conductividad térmica de los nanomateriales puede incrementarse sorprendentemente debido al cambio inducido por el acoplamiento de la banda de fonones al vector de onda baja [43]. Recientemente, también se ha informado de un estudio teórico sobre el efecto del sustrato de la conductividad térmica del grafeno. Los autores también encontraron que tanto la reducción como el incremento de la conductividad térmica pueden ser inducidos por el sustrato, dependiendo de la condición de acoplamiento [44]. De la ecuación. 3, la conductividad térmica es directamente proporcional al coeficiente de temperatura de primer orden, y es bien sabido que la figura de mérito ( ZT ) es inversamente proporcional a la conductividad térmica. Por lo tanto, bajo χ y κ prometen lograr un ZT alto .

Hay más trabajo en proceso para lograr Sb ₂ Te ₃ nanoflake con un espesor inferior a 7 QL, que es el límite de confinamiento de la TI 2D utilizando la técnica de exfoliación con ayuda de cinta adhesiva de tipo especial o mediante el uso de deposición de vapor químico. Se espera que tales escamas de bajo espesor produzcan un coeficiente de temperatura muy baja (~ 10 ^–3 a 10 ^–4 cm ⁻¹ / K) y un ZT alto . Con alto ZT , 2D Sb ₂ Te ₃ tendría un gran potencial en el campo de las aplicaciones termoeléctricas.

Conclusiones

En conclusión, hemos sintetizado con éxito 2D Sb ₂ Te ₃ de varios espesores en el rango de 65 a 400 nm mediante exfoliación mecánica y estudiaron la termometría de estas nanoflakes. La dependencia de la temperatura de la posición del pico y el ancho de línea de los modos de fonón A ² _1g y E ² _g Se analizaron los modos para determinar el coeficiente de temperatura, que se encuentra en el orden de 10 ^–2 cm ⁻¹ / K. El coeficiente de temperatura en la dirección fuera del plano disminuye con la disminución de Sb ₂ Te ₃ grosor. Un coeficiente de temperatura tan baja favorecería lograr un ZT alto y allanar el camino para utilizar este material como excelentes candidatos de materiales termoeléctricos. Usando valores de coeficiente de temperatura y coeficiente de potencia, la conductividad térmica de 115 nm Sb ₂ Te ₃ escamas compatibles con SiO ₂ de 300 nm / El sustrato de Si se estimó en ~ 10 W / m – K. La conductividad térmica ligeramente más alta en comparación con otros TI sugiere que el sustrato de soporte afecta significativamente la disipación de calor del Sb ₂ Te ₃ escamas.

Disponibilidad de datos y materiales

Los datos que respaldan los hallazgos de este estudio están disponibles del autor correspondiente a solicitud razonable.

Abreviaturas

TI:: Aisladores topológicos
ZT :: Figura de mérito
OM:: Micrografía óptica
AFM:: Microscopía de fuerza atómica
FWHM :: Ancho completo a la mitad del máximo
QL:: Capa quíntuple

Una guía de ondas flexible y estirable basada en nanograbados para detección táctil Transistor de efecto de campo de capacitancia negativa ZrOx con comportamiento de oscilación sub-60 subumbral

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias