Dispersión en ángulos pequeños de fractales gordos a nanoescala

Resumen

Se considera que la dispersión de ángulo pequeño (de neutrones, rayos X o luz; SAS) describe las características estructurales de los fractales de grasa deterministas a nanoescala. Mostramos que en el caso de un sistema fractal polidisperso, con igual probabilidad para cualquier orientación, se obtienen las dimensiones fractales y factores de escala en cada nivel estructural. Esto está de acuerdo con los resultados generales deducidos en el contexto del análisis de dispersión de ángulo pequeño de un sistema de nano- / micro-fractales orientados aleatoriamente, que no interactúan. Aplicamos nuestros resultados a un fractal gordo bidimensional similar a Cantor, calculando expresiones analíticas para las intensidades de dispersión y los factores de estructura. Explicamos cómo se pueden calcular las propiedades estructurales a partir de datos experimentales y mostramos su correlación con la variación del factor de escala con el número de iteración. El modelo se puede utilizar para interpretar datos SAS experimentales registrados en el marco de fractales gruesos y puede revelar propiedades estructurales de materiales caracterizados por una ley regular de cambio de las dimensiones fractales. Puede describir sucesiones de decaimientos de la ley de potencias, con valores decrecientes arbitrarios de los exponentes de dispersión, y intercalado por regiones de intensidad constante.

Introducción

Muchas estructuras jerárquicas generadas a nano y microescala tienen características geométricas que son invariables bajo dilataciones de escala, muestran auto-similitud y, por lo tanto, tienen propiedades fractales [1, 2]. Aunque los avances recientes en la ciencia de los materiales y la nanotecnología permiten la preparación de varios fractales deterministas artificiales nano / microescala, con una auto-similitud exacta [3-7], la gran mayoría de los procesos naturales generan fractales aleatorios, estadísticamente auto-similares. Se puede hacer una buena aproximación en los estudios estructurales de formaciones fractales naturales recurriendo a modelos fractales deterministas, con la misma dimensión fractal que los aleatorios. Este enfoque se utilizó con éxito para demostrar que la transferencia a través de superficies fractales aleatorias está muy cerca de la respuesta de geometrías de modelos deterministas [8]. Al introducir la polidispersidad en el algoritmo de construcción de un fractal determinista, se pueden obtener intensidades de dispersión de ángulo pequeño (SAS) similares a las correspondientes a los fractales aleatorios [9]. Además, un enfoque "determinista" es computacionalmente más eficiente, ya que permite la descripción analítica de varias propiedades, como la forma fractal, los factores de estructura y el radio de giro.

Uno de los métodos más fiables para determinar las propiedades estructurales de fractales deterministas y aleatorios [10, 11] es el empleo de difracción de ondas en el contexto de la dispersión de ángulos pequeños en materiales nano o microestructurados, utilizando neutrones u ondas electromagnéticas (x -rayos, luces, etc.) [12]. Es por ello que una de las tareas fundamentales en las descripciones teóricas vinculadas a las determinaciones experimentales en esta área de investigación es revelar la relación entre la estructura de los fractales y su correspondiente espectro de difracción o distribución de intensidad de dispersión vs. vector de onda de dispersión. Se llevaron a cabo muchos estudios experimentales y teóricos en esta dirección [13-21].

Usando cálculos teóricos estándar e interpolación, el parámetro que se determina a partir de este tipo de medidas experimentales es la dimensión fractal de masa D _m (ver Apéndice 1), con D _m D _s , con d −1 < D _s < d . Denotamos con d la dimensión euclidiana en la que está incrustado el fractal. La dimensión fractal de masa describe la forma en que la masa M ( r ) varía cuando está incrustado en un disco de radio r . El radio de masa obtenido relación \ (M (r) \ propto r ^ {D _ {\ mathrm {m}}} \) conduce al comportamiento de la intensidad de dispersión \ (I (q) \ propto q ^ {- D _ {\ mathrm {m} }} \). Evidentemente, D _m se puede identificar con el exponente de la dependencia de la ley de potencias de la intensidad de dispersión en función del vector de onda de dispersión q [18, 22]. Cuanto mayor sea el valor de D _m , cuanto más compacta es la estructura. De manera similar, en el caso de un fractal de superficie, su distribución de superficie obedece a \ (S (r) \ propto r ^ {2-D _ {\ mathrm {s}}} \), y por lo tanto, \ (\ phantom {\ dot { i} \!} I (q) \ propto q ^ {- (2 \ mathrm {d} -D _ {\ mathrm {s}})} \) [19, 23]. Trabajando en el espacio euclidiano tridimensional, D _s se acerca al mínimo de dos, cuando la superficie es casi perfectamente lisa. Tiende al máximo de tres, si está tan doblado que llena casi por completo el espacio.

Muchas intensidades de difracción experimentales de diversos sistemas biológicos y sintetizados químicamente se caracterizan, en una escala logarítmica doble, por una sucesión de desintegraciones de la ley de potencias, intercaladas por regiones de intensidad constante. Este comportamiento se puede identificar para algunos geles poliméricos [24], glucósido hidrolasa para el sustrato de celobiosa [25], complejos polielectrolíticos coacervados [26] o carbono nanoporoso [27]. Aunque el modelo clásico de Beaucage [28] puede proporcionar información estructural básica sobre estos sistemas (es decir, dimensión fractal de masa o superficie y el tamaño total de cada nivel estructural), se necesita una caracterización más completa debido a la gran cantidad de configuraciones que corresponden a un valor fijo de la dimensión fractal. Este problema fue abordado parcialmente recientemente por Cherny et al. [29] en el contexto de los modelos de dispersión de ángulo pequeño (SAS). Se demostró que, para fractales de masa deterministas con una sola escala, se puede obtener información adicional, como el número de iteración fractal, el número de unidades constituyentes básicas y el factor de escala. Además, este enfoque se utilizó con éxito para desarrollar nuevos modelos de fractales gordos, si las sucesiones de desintegraciones de la ley de potencias están presentes en las distribuciones de dispersión. Se puede aplicar a estructuras donde el tamaño total de las unidades de componentes básicos es del mismo orden que las distancias entre ellas [30, 31].

El modelo teórico presentado en este artículo combina modelos anteriores para ampliar su aplicabilidad. Describe sucesiones de decaimientos de la ley de potencias, con valores decrecientes arbitrariamente de los exponentes de dispersión, y intercalado por regiones de intensidad constante. Nuestro modelo también es capaz de proporcionar información más detallada sobre cada nivel estructural en el nano- / micro-fractal. Para este propósito, consideramos un fractal grueso, representado por un fractal de masa determinista bidimensional con un factor de escala que depende del número de iteración, pero con un área de superficie que no desaparece en el límite de un gran número de iteraciones, por lo que con un factor de escala positivo Medida de Lebesgue. Derivamos expresiones analíticas de la forma fractal y los factores de estructura, y mostramos cómo determinar las dimensiones fractales y los factores de escala en cada nivel estructural.

Antecedentes teóricos

Considerando una matriz de aperturas de difracción idénticas y orientadas de manera similar, indicadas aquí por Σ , que contiene N regiones transparentes, etiquetadas con j , se debe tener en cuenta una suma de las amplitudes obtenidas de cada apertura. Entonces, la conocida distribución de frecuencia de la amplitud de difracción de una sola apertura (Ec. (37) en el Apéndice 2) se puede reescribir como [32]:

$$ A (p, s) =\ suma \ límites_ {j =1} ^ {N} \ iint \ límites _ {- \ infty} ^ {~~~ + \ infty} T (x, y) e ^ {- 2 i \ pi \ left (p (x + x_ {j}) + s (y + y_ {j}) \ right)} \ mathrm {d} x \, \ mathrm {d} y. $$ (1)

Las coordenadas de un punto en el marco local de j la apertura son ( x _j , años _j ) y T ( x, y ) representa la función de transmisión individual correspondiente a cada región transparente. Se puede intercambiar sumatoria con integración porque, en nuestro caso, las aberturas están descritas por la misma función de distribución individual, por lo que la Ec. (1) se puede reescribir como:

$$ A (p, s) =\ iint \ limits _ {- \ infty} ^ {~~~ + \ infty} T (x, y) e ^ {- 2 i \ pi (px + sy)} \ mathrm { d} x \, \ mathrm {d} y \ times \ sum \ limits_ {j =1} ^ {N} e ^ {ipx_ {j}} e ^ {isy_ {j}}. $$ (2)

El factor integral de la igualdad anterior representa la transformada de Fourier de la función de distribución de cada una de las aberturas idénticas, como se señaló anteriormente. Esta amplitud está modulada por el factor que contiene la suma, que representa la transformada de Fourier de las distribuciones de Dirac-delta de la forma \ (A _ {\ delta} ~ =~ \ sum _ {j ~ =~ 1} ^ {N} (x ~ - ~ x_ {j}) (y ~ - ~ y_ {j}) \). Por tanto, también se tiene en cuenta la distribución espacial de las aberturas dentro de la matriz. Por tanto, la ecuación. (2) se puede reescribir en la forma conocida como el teorema de la matriz [32]:

$$ A (p, s) ~ =~ \ mathcal {F} \ left \ {T (x, y) \ right \} \ mathcal {F} \ left \ {A _ {\ delta} \ right \}. $$ (3)

La distribución de intensidad de la imagen difractada en el plano de Fourier se convierte en:

$$ I (p, s) \ equiv \ left | A (p, s) \ right | ^ {2} =\ left | \ mathcal {F} \ left \ {T (x, y) \ right \} \ right | ^ {2} \ big | \ mathcal {F } \ left \ {A _ {\ delta} \ right \} \ big | ^ {2}. $$ (4)

Como era de esperar, el primer factor en el producto corresponde a la intensidad de dispersión de un solo agujero, mientras que el segundo revela la forma en que estos agujeros se distribuyen dentro de la apertura de difracción Σ . Estas cantidades también se conocen como factor de forma F ( p, q ) y, respectivamente, el factor de estructura S ( p, q ). Por eso, los resultados obtenidos a lo largo del trabajo se expresarán utilizando la siguiente forma de intensidad de dispersión:

$$ I (p, q) \ equiv F (p, s) S (p, s). $$ (5)

Modelo y método fractal grueso

El procedimiento detallado para construir un fractal de Cantor delgado (regular) es bien conocido [33]. Aquí solo se resume el procedimiento de construcción principal. Se adopta un enfoque de arriba a abajo. Comenzando con un cuadrado inicial (o cualquier otra forma euclidiana) de borde l ₀ (a m =0), cuyo centro coincide con el origen del sistema de coordenadas cartesiano y aristas paralelas a los ejes del sistema de coordenadas, cualquier punto en el cuadrado satisface las condiciones - l ₀ / 2≤ x ≤ l ₀ / 2 y - l ₀ / 2≤ años ≤ l ₀ / 2. En la primera iteración ( m =1), el cuadrado se divide en otros cuatro cuadrados, con una longitud de borde \ (\ beta _ {\ mathrm {s}} ^ {(1)} l_ {0} \). Denotamos con \ (\ beta _ {\ mathrm {s}} ^ {(1)} \ equiv (1- \ gamma _ {1}) / 2 \), con \ (0 <\ beta _ {\ mathrm { s}} ^ {(1)} <1/2 \), el primer factor de escala de iteración, y con γ ₁ la fracción de la longitud eliminada en este punto, como se puede ver en la Fig. 1 a, b) para m =1. El número colocado entre (⋯), que aparece como índice superior, cuantifica el número de iteración. No debe interpretarse como un exponente de una función de potencia. En términos del factor de escala, las posiciones de los cuatro cuadrados vienen dadas por los vectores \ (\ boldsymbol {a} _ {j} ~ =~ \ left \ {\ pm \ beta _ {\ mathrm {t}} ^ { (1)} l_ {0}, \ pm \ beta _ {\ mathrm {t}} ^ {(1)} l_ {0} \ right \} \) con todas las combinaciones de signos posibles, donde \ (\ beta _ { \ mathrm {t}} ^ {(1)} ~ =~ \ left (1- \ beta _ {\ mathrm {s}} ^ {(1)} \ right) / 2 \) se usa para simplificar aún más las formulaciones. Se eligió el cuadrado como forma inicial, debido a la simplicidad de los cálculos numéricos. Se puede considerar cualquier otra forma geométrica, por ejemplo un círculo. El efecto de elegir otra forma se observa solo en la región de Porod del factor de forma, que está más allá del alcance de este documento.

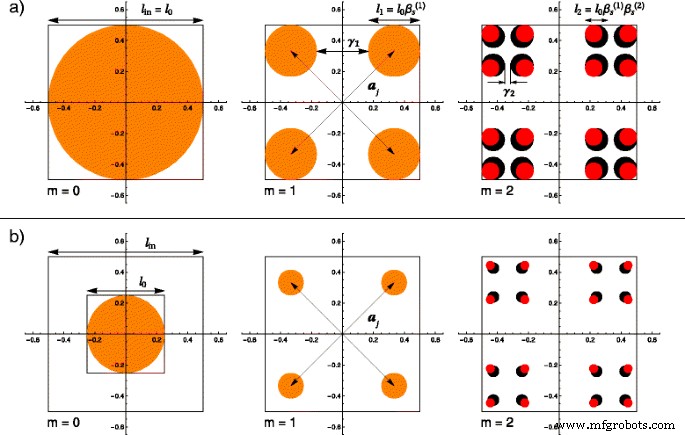
(Color en línea) Una comparación entre fractales regulares y gruesos para las dos primeras iteraciones, donde la forma básica en m =0 es un disco de diámetro l ₀ y el tamaño fractal es l _en : a l ₀ = l _en; b l ₀ = l _en / f , con f =2. En ambos casos, a m =1 las estructuras coinciden debido a factores de escala iguales \ (\ beta _ {\ mathrm {s}} ^ {(1)} \). Comenzando con m =2, el fractal grueso tiene un factor de escala mayor \ (\ left (\ beta _ {\ mathrm {s}} ^ {(2)}> \ beta _ {\ mathrm {s}} ^ {(1)} \ derecha) \), por lo que los discos tienen un diámetro mayor ( discos negros ) que en el caso de fractal regular ( discos rojos ); a _j son los vectores de posición y γ _i son las fracciones de longitud eliminada en i a iteración

Los dos primeros pasos descritos anteriormente también se aplican en la construcción de la versión clásica de un fractal grueso, para iteraciones m =0 y m =1. Por eso, hasta ahora, estas dos estructuras coinciden. Para obtener el fractal gordo, una modificación del algoritmo utilizado en la iteración m =1 debe hacerse eligiendo otro factor de escala en m =2, \ (\ beta _ {\ mathrm {s}} ^ {(2)} \ equiv (1 - \ gamma _ {2}) / 2 \). Aplicando todo el algoritmo en el límite de un gran número de iteraciones [34, 35], se vuelve a obtener la versión clásica de un fractal grueso. De la construcción se desprende claramente que la versión regular del fractal se recupera cuando los factores de escala, en cada iteración, se eligen para que sean iguales \ (\ beta _ {\ mathrm {s}} ^ {(1)} ~ =~ \ beta _ {\ mathrm {s}} ^ {(2)} ~ =~ \ cdots =\ beta _ {\ mathrm {s}} ^ {(m)} \).

Para obtener la meseta constante entre dos decaimientos de la ley de potencias en el comportamiento de la intensidad SAS, debemos tener en cuenta que las distancias entre las unidades de dispersión son mucho mayores que su tamaño total. Este enfoque se utilizó por primera vez en el contexto de modelos fractales de superficie [36, 37]. Considerando la proporción f de la distancia total entre las unidades de dispersión l _en y su tamaño total l ₀ , uno tiene:

$$ f ~ \ equiv ~ l _ {\ text {in}} / l_ {0}. $$ (6)

Para experimentos de dispersión que muestran mesetas de intensidad constante entre dos regiones fractales, valores de f Se debe elegir ≫1. En el caso de fractales superficiales, aumentar el valor de f conduce a una mejor concordancia entre la intensidad SAS total, por un lado, y la aproximación de unidades de dispersión independientes, por el otro [36, 37].

Usando las consideraciones anteriores, se pueden describir las diferencias entre fractales regulares y gruesos. La influencia del factor f , presentado anteriormente, también se puede visualizar. Es por esto que, en la Fig.1, ejemplificamos gráficamente la comparación usando un disco de radio r ₀ ≡ l ₀ / 2 = l _en / (2 f ) como nuestra forma básica. Los resultados de las dos primeras iteraciones, que se muestran en cada fila de la Fig.1, representan las estructuras obtenidas para un fractal regular (marcado por discos rojos) y un fractal grueso (representado como un disco negro), que también pueden superponerse totalmente ( marcados como discos naranjas). En la fila etiquetada como Fig. 1 a, el factor f se considera igual a la unidad para que se obtengan las construcciones clásicas y las formas fractales. La segunda fila de la figura, denominada Fig. 1 b, muestra la influencia del factor presentado anteriormente. En estos cálculos, elegimos el valor arbitrario de f =2. Se observa que en iteraciones m =0 y m =1, en los casos ayb, las estructuras obtenidas de los conjuntos Cantor regular y gordo son idénticas y están completamente superpuestas. Esto es de esperar debido al factor de escala común. Sin embargo, como se puede ver en el último par de imágenes de la Fig.1, comenzando con m =2, los radios de los discos del fractal gordo son mayores porque su factor de escala \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) es mayor, por definición, que el del normal. En la última imagen de la Fig. 2 b, el tamaño de los discos es mucho menor que en su contraparte de la Fig. 2 a debido al valor no unitario del factor f .

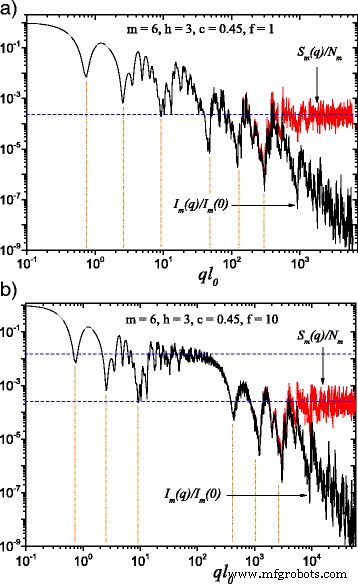
(Color en línea) Una comparación entre la intensidad de dispersión dada por la Ec. (22) ( curvas negras ) y factor de estructura dado por la Ec. (24) ( curvas rojas ) en m =6 y promediado sobre las orientaciones de acuerdo con la Ec. (25). Aquí, h =3 (es decir, el factor de escala se mantiene constante durante tres iteraciones consecutivas), mientras que la forma básica para calcular la intensidad de la dispersión es un cuadrado de tamaño de borde l ₀ : a l ₀ = l _en; b l ₀ = l _en / f (con f =10). Cuando f ≠ 1, aparece una meseta de intensidad constante entre las dos desintegraciones de la ley de potencias generalizadas (Fig. 2 b). Líneas horizontales denotar la asíntota del factor de estructura ≃1 / N _m , mientras que las posiciones mínimas se estiman según la Eq. (26)

Para obtener las leyes de potencia en sí mismas, es necesario generalizar aún más el modelo clásico de fractal grueso. Esto se hace considerando que los cambios en el factor de escala no se realizan con cada iteración, sino cada segundo, tercero, ⋯ o, en general, cada h th iteración. La fracción de longitudes eliminadas en los m la iteración es:

$$ \ gamma_ {m} ~ =~ c ^ {p_ {m}}, $$ (7)

con 0 < c <1. La función p _m se define como:

$$ p_ {m} \ equiv \ left \ lfloor 1+ \ frac {m-1} {h} \ right \ rfloor, $$ (8)

para cualquier valor entero positivo de m , con h =1, ⋯, m , donde se utilizó la función de suelo ⌊ ⋯ ⌋. Por tanto, el factor de escala correspondiente a m La iteración viene dada por:

$$ \ beta _ {\ mathrm {s}} ^ {(m)} ~ =~ \ frac {1- \ gamma_ {m}} {2}. $$ (9)

Ahora está claro que el propósito de la función p _m es mantener constante el factor de escala para h iteraciones ( h < m ).

Los componentes de los vectores de posición de cada cuadrado se pueden escribir como:

$$ \ beta _ {\ mathrm {t}} ^ {(m)} =\ frac {\ beta _ {\ mathrm {s}} ^ {(m)}} {2} + \ frac {\ gamma_ {m}} {2}, $$ (10)

mientras que la longitud del borde de cada cuadrado viene dada por:

$$ l_ {m} =\ frac {l_ {0}} {2 ^ {m}} \ prod_ {i =1} ^ {m} (1- \ gamma_ {i}). $$ (11)

El factor f se utilizará en la fórmula de la longitud l ₀ para tener en cuenta que para iteraciones entre el ( h +1) th y m th, el tamaño de los cuadrados disminuye con respecto a las distancias entre ellos:

$$ l_ {0} =\ left \ {\ begin {array} {ll} l _ {\ text {in}}, &\ mathrm {para ~~ iteraciones ~~} \ leq h \\ l _ {\ text {in }} / f, &\ mathrm {para ~~ iteraciones ~~}> h, \ end {matriz} \ right. $$ (12)

donde h < m . El número de cuadrados en cada iteración es:

$$ N_ {m} ~ =~ 4 ^ {m}. $$ (13)

Así, en cada escala, considerada como iteración con factor de escala constante, se tiene una dimensión fractal diferente dada por [29, 38, 39]:

$$ D _ {\ mathrm {m}} ~ =~ - \ frac {2 \ ln 2} {\ ln \ beta _ {\ mathrm {s}} ^ {(m)}}. $$ (14)

En el límite de un gran número de iteraciones, la dimensión fractal del conjunto fractal construido será [34]:

$$ D \ equiv \ lim \ limits_ {m \ rightarrow \ infty} {\ frac {\ ln N_ {m}} {\ ln (l_ {0} / l_ {m})}} =2, $$ (15 )

que es el valor esperado para un fractal gordo bidimensional. Finalmente, si a _i es el área relativa eliminada en i th iteración, entonces \ (\ prod _ {i =1} ^ {m} (1-a_ {i})> 0 \) si \ (\ sum _ {i =1} ^ {\ infty} a_ {i} <\ infty \), y por lo tanto, el modelo satisface la definición y características de los fractales gordos [35].

Resultados y discusión

Según el principio de Babinet, podemos concluir que en m En la iteración, las aberturas en la rejilla son los cuadrados restantes en el fractal, mientras que las partes removidas se vuelven opacas a la radiación.

Intensidad de dispersión monodispersa y factor de estructura

Para derivar la expresión analítica de la intensidad de dispersión para el fractal de Cantor gordo, comenzamos escribiendo la relación de recurrencia de la transmitancia de la rejilla para una iteración arbitraria correspondiente a 1 D caso. En m =0, tenemos

$$ T_ {0} (l_ {0}, x) \ equiv \ text {rect} (l_ {0}, x) =\ left \ {\ begin {array} {ll} 1, &| x | Teniendo en cuenta el algoritmo de construcción del fractal, la transmitancia después de la primera iteración viene dada por:

$$ \ begin {alineado} T_ {1} (l_ {1}, x,) =T_ {0} (l_ {1}, x) \ ast \ delta \ left (\ frac {x-l_ {0} \ beta _ {\ mathrm {t}} ^ {(1)}} {l_ {1}} \ right) + \\ T_ {0} (l_ {1}, x) \ ast \ delta \ left (\ frac {x + l_ {0} \ beta _ {\ mathrm {t}} ^ {(1)}} {l_ {1}} \ right), ~~~~~~~~~~~~ \ end {alineado} $$ (17)

donde δ ( x - a ) es la distribución unidimensional de Dirac-delta en x = a . El símbolo ∗ representa el operador de convolución. Por lo tanto, en m th iteración, podemos escribir:

$$ \ begin {alineado} T_ {m} (l_ {m}, x) =T_ {m-1} (l_ {m}, x) \ ast \ delta \ left (\ frac {x-u_ {m} } {l_ {m}} \ right) + \\ T_ {m-1} (l_ {m}, x, y) \ ast \ delta \ left (\ frac {x + u_ {m}} {l_ {m }} \ derecha), ~~~~~~~~~~~~ \ end {alineado} $$ (18)

donde \ (u_ {m} ~ =~ l_ {0} \ beta _ {\ mathrm {t}} ^ {(m)} \ prod _ {j =1} ^ {m-1} \ beta _ {\ mathrm {s}} ^ {(j)} \). Realizando una transformada de Fourier en la ecuación. (18), se encuentra que la amplitud dispersa en m la iteración es:

$$ A_ {m} (p) =2 ^ {m} \ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ prod \ limits_ {i =1} ^ { m} \ cos (2 \ pi p u_ {i}). $$ (19)

Desde la 2 D El modelo fractal gordo es un producto directo de dos fractales gordos unidimensionales, su transformada de Fourier se puede escribir como un producto de dos transformadas de Fourier unidimensionales. Por lo tanto, la amplitud de dispersión bidimensional se puede escribir como:

$$ A_ {m} (p, s) \ equiv A_ {m} (p) A_ {m} (s), $$ (20)

y así,

$$ \ begin {alineado} A_ {m} (p, s) =N_ {m} \ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin (\ pi s l_ {m})} {\ pi s l_ {m}} \ times \\ \ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}), \ end {alineado} $$ (21)

de modo que la intensidad de dispersión se convierta en:

$$ \ begin {alineado} I_ {m} (p, s) =\ left (\ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin ( \ pi s l_ {m})} {\ pi s l_ {m}} \ right) ^ {2} \ times \\ N_ {m} ^ {2} \ left (\ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}) \ right) ^ {2}. \ end {alineado} $$ (22)

El primer factor de la ecuación anterior, que representa la intensidad de difracción debida al factor de forma, como se indica en la Ec. (5):

$$ F_ {m} (p, s) =\ left (\ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin (\ pi s l_ { m})} {\ pi s l_ {m}} \ derecha) ^ {2}, $$ (23)

corresponde a la intensidad de dispersión obtenida de un solo cuadrado de borde l _m . El segundo factor, que representa la intensidad de difracción debida al factor de estructura, como se indica en la Ec. (5):

$$ S_ {m} (p, s) =N_ {m} ^ {2} \ left (\ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}) \ derecha) ^ {2}, $$ (24)

describe la forma en que se distribuyen los cuadrados. La intensidad de la radiación dispersada total es el producto de F _m ( p, s ) y S _m ( p, s ).

El decaimiento de la intensidad según la ley de potencias, como se formula en la Ec. (22), se obtiene después de realizar la media de todas las orientaciones [29]. Considerando la misma probabilidad para cualquier orientación, el promedio se puede calcular en el caso de fractales bidimensionales mediante la integración en todas las direcciones del vector de dispersión q =( p, s ):

$$ \ langle f (p, s) \ rangle =\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} f (q, \ phi) \ mathrm {d} \ phi, $ $ (25)

donde p = q porque ϕ y s = q pecado ϕ . Por lo tanto, la intensidad de dispersión I ( q ) se obtiene en función del módulo de transferencia de momento q ≡ | q |.

Porque, de la definición de factor de estructura, uno tiene \ (S_ {m} (0) ~ =~ N_ {m} ^ {2} \), donde N _m es el número de cuadrados, como se define en la Ec. (13), el procedimiento estándar de normalización S _m (0) =1 se puede adoptar, como se describe en [11, 29].

Los resultados calculados para la intensidad de dispersión monodispersa I _m ( q ) y factor de estructura S _m ( q ), con m =6, se muestran en la Fig.2 para el fractal gordo clásico ( f =1 en la Fig.2 a) y, para el modelo fractal de grasa extendido desarrollado en este trabajo ( f =10 en la Fig. 2 b). Para obtener la Fig. 2 b, consideramos h =3 para que el factor de escala \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) de las primeras tres iteraciones se mantuviera constante, luego tenía otro valor constante \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) para las próximas tres iteraciones. Como se esperaba, en ambos casos (para f =1 y f =10), las diferencias entre la intensidad de dispersión, por un lado, y el factor de estructura, por el otro, se pueden observar cuando \ (q \ gtrsim 1 / l_ {m} \). En esta región, la intensidad de dispersión tiene una disminución de la ley de potencia I ( q ) ∝ q ⁻³ . El factor de estructura tiene un valor asintótico que tiende a 1 / N _m , representada por la línea horizontal en la Fig. 2 a o la línea horizontal inferior en la Fig. 2 b [29, 33].

En la figura 2a se puede ver una sucesión de dos desintegraciones de ley de potencias generalizadas, identificables como una superposición de máximos y mínimos, sobre una desintegración de ley de potencias simple. Pero en la Fig.2 b, una región de intensidad aproximadamente constante, en el dominio 20≲ ql ₀ ≲100, se puede distinguir claramente, englobado por las dos desintegraciones sucesivas de leyes de potencia generalizadas. Esto se debe a la disminución del tamaño de los cuadrados en un orden de magnitud ( f =10) en comparación con las distancias entre ellos. Esta región, observable alrededor de la línea horizontal superior en la Fig.2 b tiene la asíntota 1 / N ₃ , el mismo que el del factor de estructura del fractal gordo clásico, mostrando un comportamiento similar al caso de considerar solo las tres primeras iteraciones.

Además, se puede ver en la Fig. 2 que el número de mínimos en cada escala coincide con el número de iteraciones de factor de escala constante. Estos mínimos ocurren cuando la radiación que pasa a través de diferentes cuadrados dentro del fractal interfiere y están en oposición de fase, y por lo tanto, las distancias más frecuentes entre el centro de los cuadrados (2 u _m ) son iguales a π / q . Por eso, las posiciones aproximadas de los mínimos se obtienen de la relación:

$$ q_ {i} \ simeq \ frac {\ pi} {2 u_ {i}}, ~~~~ i =1, \ cdots, m $$ (26)

indicado en la Fig. 2 mediante líneas verticales. Para las primeras seis iteraciones, se observa una concordancia bastante buena entre las posiciones calculadas usando la Ec. (26), y los encontrados en la intensidad de dispersión o factor de estructura. Esta aproximación podría ser menos precisa para iteraciones más altas, una vez que el número de iteración aumenta por encima de un cierto valor porque en estos casos, cada vez más distancias son comparables a las que se encuentran con más frecuencia. No obstante, esta aproximación funcionará bastante bien en la práctica, donde difícilmente se puede esperar distinguir más de cuatro o cinco de esos mínimos.

Para cada escala individual, en un rango dado 1 / (2 u _i ) ≲ q ≲1 / (2 u _{i +1} ), el patrón de difracción es producido por la interferencia de solo i ª iteración fractal. Esto puede usarse para mostrar que, dentro de este intervalo, las funciones I _m ( q ) q ^D y S _m ( q ) q ^D son logarítmicas periódicas [29], donde D es la dimensión fractal correspondiente a una escala dada. En particular, para los resultados mostrados en las Figs. 2 y 3, las funciones I _m ( q ) q ^−1.1 y S _m ( q ) q ^−1.1 son logarítmicas periódicas con el período \ (1 / \ beta _ {\ mathrm {s}} ^ {(1)} \) para las tres primeras iteraciones, mientras que I _m ( q ) q ^−1.51 y S _m ( q ) q ^−1.51 son logarítmicas periódicas con \ (1 / \ beta _ {\ mathrm {s}} ^ {(2)} \) para el segundo grupo de tres iteraciones.

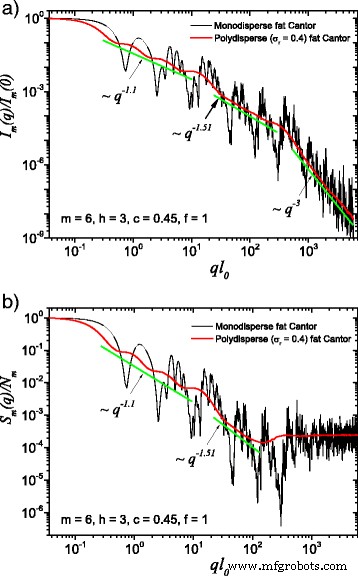
(Color en línea) Una comparación entre sistemas monodispersos y polidispersos: a intensidad de dispersión (ecuación (22)); b factor de estructura (Ec. (24)), promediado sobre todas las orientaciones del fractal, de acuerdo con la Ec. (25). Aquí, f =1, m =6, h =3 (es decir, el factor de escala se mantiene constante durante tres iteraciones consecutivas), y la forma básica es un cuadrado de longitud de borde inicial l ₀ = l _en . Para ambos casos, la polidispersidad difumina las curvas de dispersión monodispersas y las dimensiones fractales se pueden recuperar en cada nivel estructural

De manera similar a los fractales de masa deterministas, la Ec. (26) se puede utilizar para obtener varios parámetros estructurales que caracterizan los fractales grasos. Primero, el número total de mínimos coincide con el número total de iteraciones fractales. La Figura 2 muestra que el fractal consta de tres iteraciones con factor de escala \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) y tres iteraciones con factor de escala \ (\ beta _ {\ mathrm {s} } ^ {(2)} \). En segundo lugar, a partir de la periodicidad de estos mínimos (o de la periodicidad de I _m ( q ) q ^D y S _m ( q ) q ^D ), los factores de escala se pueden recuperar. En la Fig. 2 b, el factor de escala \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) se puede obtener a partir de la periodicidad de los mínimos en ql ₀ ≃7,25 y 90, mientras que el factor de escala \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) se puede obtener a partir de la periodicidad de los mínimos en ql ₀ ≃400,1000 y 2500. Además, la longitud de la meseta intermedia entre regiones fractales se puede utilizar como una indicación de la relación ( f ) de las distancias entre las unidades de dispersión y su tamaño total. En la Fig. 2 b, este rango corresponde a 13≲ ql ₀ ≲130.

Intensidad de dispersión polidispersa y factor de estructura

En esta parte de nuestro trabajo, podemos considerar ahora que los tamaños de las rejillas obedecen a una función de distribución D _N ( l ₀ ), definido de tal manera que D _N ( l ₀ ) d l ₀ da la probabilidad de que el tamaño de la rejilla fractal esté en el intervalo ( l ₀ , l ₀ + d l ₀ ). Este paso introduce la polidispersidad en nuestro modelo fractal gordo. Ejemplificamos esto eligiendo una distribución logarítmica normal:

$$ D _ {\ mathrm {N}} (l_ {0}) =\ frac {1} {\ sigma l_ {0} (2 \ pi) ^ {1/2}} e ^ {- \ frac {\ left (\ log (l_ {0} / \ mu) + \ sigma ^ {2} / 2 \ right) ^ {2}} {2 \ sigma ^ {2}}}, $$ (27)

con varianza relativa \ (\ sigma _ {\ mathrm {r}} =\ left (\ left \ langle l_ {0} ^ {2} \ right \ rangle _ {D} - \ mu ^ {2} \ right) ^ {1/2} / \ mu \), valor medio μ =〈 l ₀ 〉 _D , and variance $\sigma =\left (\log \left (1+\sigma _{\mathrm {r}}^{2}\right)\right)^{1/2}$. Using Eqs. (21) and (27) one obtains the polydisperse intensity averaged over the distribution function:

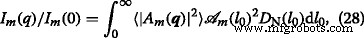
donde is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term [29].

The computed results in the case of polydisperse (red curves) and monodisperse (black curves) scattering intensities (labeled by a) and structure factors (labeled by b) can be seen in Figs. 3 and 4. The difference between them is given by the value of the f factor. In Fig. 3, the classical construction of a fat fractal was used so that f =1, while taking into account the smaller sizes of the basic units leads to the choice of f =10 in Fig. 4. Polydispersity is calculated for a relative variance of σ _r =0.4. It can be seen that the oscillations are smeared out, the overall amplitude decreases, so that the scattering curves become smoother [29, 40]. However, for this particular value of σ _r , the positions of main minima and maxima are still observable.

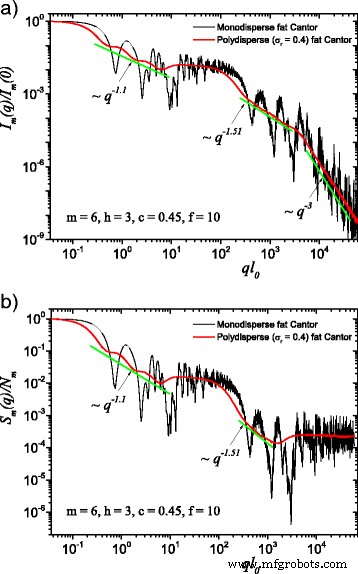
(Color online) A comparison between monodisperse and polydisperse systems:a scattering intensity (Eq. (22)); b structure factor (Eq. (24)), averaged over all orientations of the fractal, according to Eq. (25). Here, f =10 (and thus, a region of constant intensity appears at about 20≲ql ₀ ≲100), m =6, h =3 (i.e., the scaling factor is kept constant for three consecutive iterations), and the basic shape is a square of initial edge length l ₀ =l _in . For both cases, the polydispersity smears out monodisperse scattering curves, and the fractal dimensions can be recovered at each structural level

More generally, for small values of σ _r (i.e., small enough that the oscillations are observable), the estimation given by Eq. (26) can be still used. Hence, the number of fractal iterations, the scaling factor at each structural level, the ratio of the distances between scattering units, and their overall size can be recovered. When σ _r is increased to high enough values so that oscillations are completely smeared out, the scattering curves become simple power-law decays. Since we used a narrow bell-shaped distribution, the scattering exponent is preserved. Moreover, it gives, for each power-law decay, the fractal dimension of that particular structural level. This is in good agreement with the theoretical estimation of Eq. (14). This is also in accordance with experimental setups, where almost every scattering curve has a certain degree of polydispersity. Thus, our developed fat fractal model, with an interleaved region of constant intensity, recovers the fractal dimension at each structural level from polydisperse experimental data.

Conclusions

In this article, we suggest a theoretical model that generalizes the standard one for nanoscale fat fractals. It is characterized by the fact that the initial edge size of the elementary unit shape is taken to be much smaller than that of the overall size of the fractal, and thus, much smaller than the distances between the elementary units inside the fractal. Figure 1 b illustrates the basic model, when a quotient of 1/2 is considered in-between these quantities, respectively.

Based on this model, an analytical formula is calculated and presented, in Eq. (22) for the scattering intensity and in Eq. (24) for the structure factor. Averaging over all possible orientations is done according to Eq. (25). These averaged quantities are characterized, on a double logarithmic scale, by the presence of two structural levels, and thus by two power-law decays interleaved by a region of constant intensity, represented by a plateau, as seen in Figs. 2 b and 4. This plateau coincides with the asymptotic region of the structure factor of the fat fractal, as if we would have considered only the contribution from the first structural level, when the scaling factor was kept constant. The asymptotic values of the plateaus can be used to obtain the number of scattering units for each structural level. The length of the plateau is controlled by the value of f . The power-law decays encompassing the plateau are obtained by keeping constant the scaling factors for a finite number of iterations, in our case, as an example, for three out of a total of six. The slope of the second power-law decay is higher because the values of scaling factors, by definition, increase at each structural level, and this is confirmed by our numerical computations, as can be seen in Figs. 2, 3, and 4.

We also described the polydisperse case of the fat fractal model. Here, the sizes of the composing units obey, as an example, a log-normal distribution function. We obtained smoothed curves for the scattering intensities and structure factors. The monodisperse scattering curves as well as the polydisperse ones, with small enough values of the relative variance, allow to obtain the scaling factors at each structural level, while the scattering exponents in the polydisperse curve give the fractal dimensions at each structural level. The chosen value of 0.4 for the relative variance is meant to illustrate the case in which one can still observe some minima in the scattering characteristics, and the curves still retain a shape close to power-law decays.

The results obtained in the framework of the suggested model can be used to reveal structural properties of fractal materials characterized by a regular law of changing of the fractal dimensions. The proposed model is also a very versatile one because it can be extended to include other features such as different shapes of the elementary unit, more than two structural levels, or it can be adapted to work in other Euclidean dimensions. These results are useful for a detailed description of experimental diffraction data in the context of small-angle scattering obtained from various complex nano- and micro- scaled hierarchical structures.

Appendix

fractal dimension

Mass and, respectively, surface fractal dimensions are probably the most important quantities that characterize a fractal. Actually, we will deal only with deterministic mass fractals, and we shall refer to mass fractal dimension, simply as the fractal dimension (D _m ).

In general terms, the mass-radius relation can be rewritten as [2]:

$$ M(r) =A(r) r^{D_{\mathrm{m}}}, $$ (29)

where the scaling law correction A (r ) tends to a constant value if r →∞ .

If it is known a priori that the structure is a fractal in the high number limit, the fractal dimension can be found straight from the first iteration. To illustrate this procedure, let us consider a fractal of size l ₀ , composed of k elementary units at the first iteration, each of size β _s l ₀ , where β _s is a scaling factor. Since the mass-radius relation, given by Eq. (29), is equivalent with the scale-invariance relation [2]:

$$ M(\beta_{\mathrm{s}}l_{0}) =\beta_{\mathrm{s}}^{D_{\mathrm{m}}}M(l_{0}), $$ (30)

one can write M (l ₀ )=kM (β _s l ₀ ). Usando la ecuación. (29), one obtains a direct method to compute the fractal dimension, via:

$$ k \beta_{\mathrm{s}}^{D_{\mathrm{m}}} =1. $$ (31)

fraunhofer diffraction and the array theorem

Let us consider a two-dimensional diffracting aperture Σ , laid in the (x,y ) plane, illuminated in the positive z direction. In an observation plane (u,v ), parallel to Σ , the complex-valued amplitude of the obtained diffraction image, computed using the framework of scalar theory of diffraction, according to the Huygens-Fresnel principle, can be written as [41]:

$$ A(u,v) =\frac{z}{i\lambda} \iint\limits_{\Sigma} A(x,y)\frac{e^{ikr}}{r^{2}} \mathrm{d} x\,\mathrm{d} y. $$ (32)

In the previous formula, $r =\sqrt {z^{2}+(u-x)^{2}+(v-y)^{2}}$ is the distance between two arbitrarily points taken, respectively, from the plane containing Σ and from the observation plane. For the Fraunhofer diffraction model to be applicable, this distance must satisfy the condition of being much bigger than the wavelength λ .

Performing a binomial expansion of the square root in Eq. (32) and retaining only the first two terms, one obtains [41]:

$$ r \approx z\left(1 + \frac{(u-x)^{2}}{2z^{2}} + \frac{(v-y)^{2}}{2z^{2}}\right). $$ (33)

This approximation leads to the Fresnel diffraction integral:

$$ \frac{A(u,v)}{P(u,v)} =\iint\limits_{-\infty}^{~~~+\infty} \left\{A(x,y) e^{i\frac{k}{2z}(x^{2} + y^{2})}\right\} e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y, $$ (34)

where the prefactor P (u,v ) is given by

$$ P(u,v) =\frac{e^{ikz}e^{i\frac{k}{2z}(u^{2}+v^{2})}}{i\lambda z}, $$ (35)

y k =2π /λ . Considering, in addition, that the condition z ≫k Max(x ² +y ² )/2 is satisfied, one has $\text {Exp}{\left (\frac {k}{2z}(x^{2}+y^{2})\right)} \simeq 1$. Rewriting Eq. (34), the Fraunhofer approximation becomes:

$$ A(u,v) =P(u,v)\iint\limits_{-\infty}^{~~~+\infty} A(x,y) e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y. $$ (36)

Denoting the spatial frequencies with p =u /(λ z ) and s =v /(λ z ) and ignoring the multiplicative phase factor P (u,v ) preceding the integral in Eq. (36), the amplitude becomes simply the Fourier transform of the distribution of the Σ aperture. Considering that the illumination is made using a monochromatic, unit-amplitude plane-wave, at normal incidence, and that the field distribution across the aperture is equal to its transmission function T (x,y ), one obtains the frequency distribution of the diffraction amplitude in the phase space:

$$ A(p,s) =\iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{-2 i \pi (px + sy)}\mathrm{d}x\,\mathrm{d}y. $$ (37)

Ingeniería del proceso de recubrimiento por inmersión y optimización del rendimiento para dispositivos electrocrómicos de tres estados Fabricación por lotes de microlentes planas metálicas de banda ancha y sus matrices que combinan el autoensamblaje de la nanoesfera con la fotolitografía convencional

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias