Conversión de numeración decimal

Debido a que los sistemas de numeración octal y hexadecimal tienen bases que son múltiplos de binario (base 2), la conversión entre hexadecimal u octal y binario es muy fácil.

Además, debido a que estamos tan familiarizados con el sistema decimal, la conversión de formato binario, octal o hexadecimal a decimal es relativamente fácil (simplemente sume los productos de valores cifrados y pesos de lugar).

Sin embargo, la conversión de decimal a cualquiera de estos "extraños" sistemas de numeración es un asunto diferente.

Método de prueba y ajuste

El método que probablemente tendrá más sentido es el método de "prueba y ajuste", en el que intenta "ajustar" la notación binaria, octal o hexadecimal al valor deseado representado en forma decimal.

Por ejemplo, digamos que quería representar el valor decimal de 87 en forma binaria. Comencemos dibujando un campo numérico binario, completo con valores de ponderación posicional:

Bueno, sabemos que no tendremos un bit "1" en el lugar de 128, porque eso nos daría inmediatamente un valor mayor que 87.

Sin embargo, dado que el siguiente peso a la derecha (64) es menor que 87, sabemos que debemos tener un "1" allí.

Si también hiciéramos el siguiente lugar a la derecha un "1", nuestro valor total sería 64 ₁₀ + 32 ₁₀ o 96 ₁₀ . Esto es mayor que 87 ₁₀ , por lo que sabemos que este bit debe ser un "0".

Si hacemos que el siguiente bit de lugar (16) sea igual a "1", esto lleva nuestro valor total a 64 ₁₀ + 16 ₁₀ o 80 ₁₀ , que está más cerca de nuestro valor deseado (87 ₁₀ ) sin excederlo:

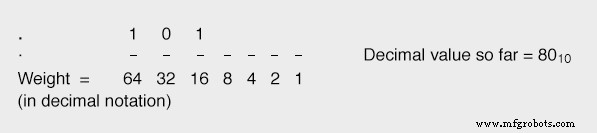
Al continuar en esta progresión, configurando cada bit de menor peso a medida que necesitamos llegar a nuestro valor total deseado sin excederlo, eventualmente llegaremos a la cifra correcta:

Método de prueba y ajuste en octal y hexadecimal

Esta estrategia de prueba y ajuste también funcionará con conversiones octales y hexadecimales. Tomemos la misma cifra decimal, 87 ₁₀ y convertirlo a numeración octal:

Si ponemos un cifrado de "1" en el lugar del 64, tendríamos un valor total de 64 ₁₀ (menos de 87 ₁₀ ). Si ponemos un cifrado de "2" en el lugar del 64, tendríamos un valor total de 128 ₁₀ (mayor que 87 ₁₀ ). Esto nos dice que nuestra numeración octal debe comenzar con un "1" en el lugar del 64:

Ahora, necesitamos experimentar con valores de cifrado en el lugar de los 8 para intentar obtener un valor total (decimal) lo más cercano a 87 como sea posible sin excederlo. Al probar las primeras opciones de cifrado, obtenemos:

Un valor de cifrado de "3" en el lugar de los 8 nos colocaría sobre el total deseado de 87 ₁₀ , entonces "2" es!

Por supuesto, si estuvo prestando atención durante la última sección sobre conversiones octales / binarias, se dará cuenta de que podemos tomar la representación binaria de (decimal) 87 ₁₀ , que previamente determinamos que era 1010111 ₂ y convertir fácilmente de eso a octal para comprobar nuestro trabajo:

¿Podemos hacer la conversión de decimal a hexadecimal de la misma manera? Seguro, pero ¿quién querría? Este método es simple de entender, pero laborioso de llevar a cabo.

Hay otra forma de hacer estas conversiones, que es esencialmente la misma (matemáticamente), pero más fácil de lograr.

Técnica de división repetida

Este otro método usa ciclos repetidos de división (usando notación decimal) para dividir la numeración decimal en múltiplos de valores de peso posicional binarios, octales o hexadecimales.

En el primer ciclo de división, tomamos el número decimal original y lo dividimos por la base del sistema de numeración al que estamos convirtiendo (binario =2 octal =8, hex =16).

Luego, tomamos la porción de número entero del resultado de la división (cociente) y lo dividimos por el valor base nuevamente, y así sucesivamente, hasta que obtenemos un cociente menor que 1.

Los dígitos binarios, octales o hexadecimales están determinados por los "restos" que quedan en cada paso de división. Veamos cómo funciona esto para binario, con el ejemplo decimal de 87 ₁₀ :

Los bits binarios se ensamblan a partir del resto de los pasos de división sucesivos, comenzando con el LSB y continuando con el MSB. En este caso, llegamos a una notación binaria de 1010111 ₂ .

Cuando dividimos por 2, siempre obtendremos un cociente que termine en ".0" o ".5", es decir, un resto de 0 o 1. Como se dijo antes, esta técnica de repetición de división para la conversión funcionará para la numeración. sistemas que no sean binarios.

Si tuviéramos que realizar divisiones sucesivas usando un número diferente, como 8 para la conversión a octal, necesariamente obtendremos restos entre 0 y 7. Intentemos esto con el mismo número decimal, 87 ₁₀ :

También podemos usar una técnica similar para convertir sistemas de numeración que se ocupan de cantidades menores que 1.

Para convertir un número decimal menor que 1 en binario, octal o hexadecimal, usamos la multiplicación repetida, tomando la porción entera del producto en cada paso como el siguiente dígito de nuestro número convertido.

Usemos el número decimal 0.8125 ₁₀ como ejemplo, convertir a binario:

Al igual que con el proceso de división repetida para números enteros, cada paso nos da el siguiente dígito (o bit) más alejado del "punto".

Con entero (división), trabajamos de LSB a MSB (de derecha a izquierda), pero con multiplicaciones repetidas, trabajamos de izquierda a derecha.

Para convertir un número decimal mayor que 1, con un componente <1, debemos usar ambos técnicas, una a la vez. Tome el ejemplo decimal de 54.40625 ₁₀ , convirtiendo a binario:

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de sistemas de numeración