Confinamiento mejorado de polaritones de plasma de superficie de terahercios en guías de ondas de metal semimetálico-aislante-metal Dirac a granel
Resumen
Se investiga una guía de onda plasmónica de terahercios de sublongitud de onda basada en una estructura a granel de semimetal de Dirac (BDS) -aislante-metal (BIM), lo que indica que existe un rango de frecuencia optimizado con el mejor confinamiento y menor pérdida. Un confinamiento del modo de banda ancha hasta λ 0 / 15 con una pérdida relativamente baja de 1.0 dB / λ 0 puede lograrse. También mostramos que dos cintas de silicio introducidas en la guía de ondas BIM pueden formar un filtro sintonizable dinámicamente que adapta polaritones de plasmón de superficie de terahercios en una escala de sublongitud de onda profunda, que se puede aprovechar aún más para el diseño de dispositivos plasmónicos THz ultracompactos con sintonización dinámica. Nuestros resultados también pueden proporcionar aplicaciones potenciales en el filtrado óptico.
Antecedentes
La onda de terahercios (THz) ha sido muy atestiguada en las últimas décadas por sus aplicaciones innovadoras, como la obtención de imágenes de THz, la detección bioquímica y las comunicaciones [1, 2, 3]. Para mejorar la sensibilidad de detección, la resolución de imágenes y el nivel de integración de los dispositivos THz, se desea con urgencia confinar la onda THz en una escala de sublongitud de onda profunda [4, 5, 6]. Los polaritones de plasmón de superficie (SPP), los modos electromagnéticos de superficie estimulados por la interacción entre el electrón en la banda de conducción de un metal noble y los fotones en las longitudes de onda visibles, se propagan a lo largo de la interfaz metal-aislante y permiten la manipulación de la luz más allá del límite de difracción clásico [7]. Los modos Sommerfeld-Zenneck, análogos de SPP en banda visible, pueden ser compatibles con metal en la región THz. Se han propuesto metamateriales y otras estructuras artificiales, como parches periódicos, placas perforadas y tubos de latón, para adaptar estas ondas superficiales sueltas [8,9,10]. Desafortunadamente, el confinamiento deficiente, la alta pérdida intrínseca y la capacidad de sintonización pasiva de este modo han obstaculizado gravemente sus aplicaciones prácticas.
Los plasmones de grafeno, con pérdidas relativamente bajas, sintonización dinámica y confinamiento extremo a las ondas THz, tienen aplicaciones prometedoras en dispositivos sintonizables dinámicos, ultracompactos y de alta resolución. Duan y col. proponen una heteroestructura de grafeno sintonizable por puerta de banda ancha para generar y controlar de manera coherente plasmones de terahercios con sintonía dinámica y mayor eficiencia. Se puede generar una señal de frecuencia de diferencia sólida debido al estrecho confinamiento del campo de plasmón de grafeno [11]. Duan y col. En primer lugar, investigue el efecto Talbot discreto en matrices de guías de onda plasmónicas de grafeno dieléctrico en longitudes de onda THz, lo que proporciona una plataforma novedosa para la autoimagen de alta resolución de ondas THz en nanoescala [12]. Lin y col. proponen una guía de ondas de transparencia ultracompacta inducida por plasmón, que promete aplicaciones potenciales en la luz lenta de las ondas THz [13, 14]. Li y col. proponen una serie de filtros ópticos funcionales y absorbentes basados en plasmones de material 2D, que demuestran una alta integración [15], bajas pérdidas y sintonía dinámica [16,17,18]. A partir de estos trabajos, podemos convencer de que es el confinamiento extremo de los plasmones de superficie lo que hace posible manipular las ondas THz a una escala de sublongitud de onda profunda.
Recientemente, los semimetales de Dirac a granel (BDS), "grafeno 3-D", se enfocan debido a su movilidad de portadora ultra alta de hasta 9 × 10 6 cm 2 V −1 s −1 , que es mucho más alto que el mejor grafeno de 2 × 10 5 cm 2 V −1 s −1 [19]. En general, cuanto mayor sea la movilidad del portador, menor será la pérdida intrínseca de plasmones. Además, las funciones dieléctricas de BDS se pueden sintonizar activamente cambiando su energía Fermi. La buena noticia es que BDS, como Na 3 Bi [19], Cd 3 Como 2 [20] y los cuasicristales AlCuFe [21], son más fáciles de procesar y más estables en comparación con el grafeno, que se espera que sea una nueva generación de material plasmónico después del grafeno. Sin embargo, el confinamiento de modo de los SPP en la interfaz BDS-aislante no es optimista. Nuestro trabajo reciente ha investigado la manipulación de los THz SPP en la guía de ondas de hoja BDS de doble capa, lo que indica que el modo de acoplamiento simétrico tiene un mejor confinamiento que el modo de guía de onda plasmónica en una película BDS monocapa [22]. El índice de modo del modo simétrico es 1,21 a 1,0 THz con la energía de Fermi de BDS E F =70 meV, que sigue siendo insuficiente para satisfacer la demanda de manipulación de ondas THz en una escala de sublongitud de onda profunda.
En este artículo, proponemos una guía de onda de metal aislante BDS de sublongitud de onda profunda (BIM) con confinamiento mejorado, pérdida relativamente baja y sintonización deseable. Se investigan la relación de dispersión, la pérdida de propagación y la aplicación de filtrado de este modo altamente confinado. Curiosamente, existe un rango de frecuencia optimizado con un confinamiento mejorado, así como una pérdida reducida, que rara vez se ha informado en el modo SPP tradicional en estructuras metálicas. Un confinamiento del modo de banda ancha hasta λ 0 / 15 con una pérdida relativamente baja de 1.0 dB / λ 0 puede lograrse. A diferencia de la estructura basada en BDS estudiada anteriormente, el modo de esta guía de ondas BIM se puede transmitir de manera eficiente a través de una rendija ultra estrecha con un ancho menor que λ 0 / 2000. Al tomar dos cintas de silicio como espejos de reflexión, se ha logrado un resonador óptico sintonizable dinámicamente. La frecuencia de resonancia del resonador se puede sintonizar dinámicamente variando la energía de Fermi de BDS, que puede encontrar aplicaciones en la conmutación y filtrado de THz.
Teoría y simulación
La guía de onda plasmónica BIM propuesta se presenta esquemáticamente en la Fig. 1 (a), donde la película BDS monocapa con un grosor de 0,2 μm se coloca con un ancho de espacio g lejos del sustrato de plata separado por el espaciador dieléctrico con permitividad ε r . El sustrato de plata en la región THz puede tratarse como un límite de conductor eléctrico perfecto (PEC). Para la luz incidente polarizada en TM, el modo de guía de onda plasmónica confinado en la interfaz metal-aislante puede propagarse a lo largo de la x dirección con un vector de onda k SPP y decaer exponencialmente a lo largo de la y dirección hacia el espacio libre. Al combinar las condiciones de contorno adecuadas, el vector de onda k SPP de la guía de ondas BIM se puede obtener a partir de la siguiente relación de dispersión:[23].
$$ - \ frac {\ varepsilon_r \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} {\ varepsilon_0 \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac { \ varepsilon_r {k} _0 ^ 2} {\ varepsilon_0}}} =\ left (1+ \ frac {i \ sigma \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} { {\ omega \ varepsilon} _0} \ right) \ tanh \ left (g \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac {\ varepsilon_r {k} _0 ^ 2} {\ varepsilon_0}} \ right ), $$ (1)donde k 0 es el vector de onda de la luz incidente. Resolviendo la ecuación. (1), podemos obtener el índice de refracción efectivo n ef = k SPP / k 0 =Re ( n ef ) + i Soy ( n ef ) de la guía de ondas plasmónica propuesta. Para los modos de guía de ondas plasmónicas altamente confinados, la parte real del índice de refracción efectivo Re ( n ef ) describen aproximadamente el modo de confinamiento, mientras que la parte imaginaria Im ( n ef ) es directamente proporcional a la pérdida de propagación del modo:la mayor Re ( n ef ) es, mayor es el confinamiento. Cuando g es lo suficientemente grande como para que tanh [ g ( k SPP 2 - ε r k 0 2 / ε 0 )] ~ 1, Ec. (1) se reduciría a la relación de dispersión
$$ - \ frac {\ varepsilon_r \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} {\ varepsilon_0 \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac { \ varepsilon_r {k} _0 ^ 2} {\ varepsilon_0}}} =\ left (1+ \ frac {i \ sigma \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} { {\ omega \ varepsilon} _0} \ derecha), $$ (2)que representa el modo de guía de onda plasmónica apoyado por una sola capa de BDS solo. La conductividad compleja de BDS se presenta en los métodos Eqs (3) - (4).
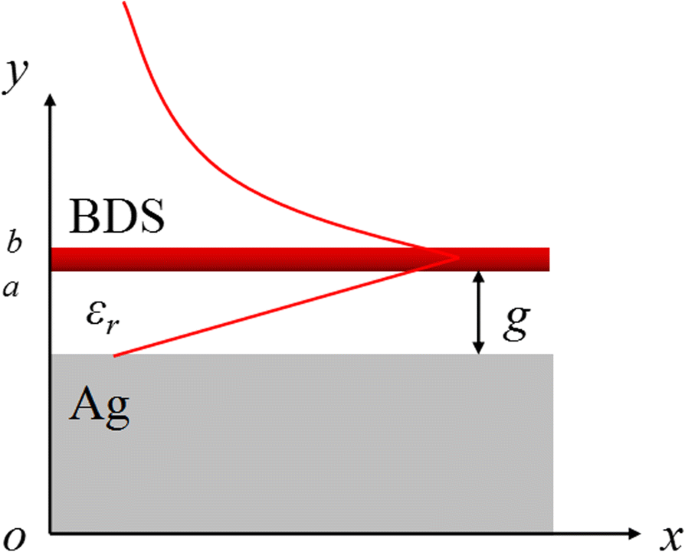
Ilustración esquemática de la guía de ondas plasmónica BIM:se coloca una película BDS monocapa con un ancho de separación g lejos del sustrato de plata separado por un espaciador dieléctrico con permitividad ε r . El modo de guía de onda plasmónica polarizada por TM se propaga a lo largo de la x dirección y decae a lo largo de la y dirección. Representación esquemática del E x la distribución está representada por la línea roja
Resultados y discusión
Primero, demostramos la dependencia del confinamiento de modo y la pérdida de propagación de la guía de ondas BIM en el ancho de brecha de metal BDS g y Fermi energy E F . Tomando E F =70 meV, calculamos los índices de refracción efectivos del modo de guía de ondas SPP n ef para diferentes valores de g , donde sus partes real e imaginaria, Re ( n ef ) y yo ( n ef ), se representan en la Fig. 2a, b, respectivamente. Como se muestra en la Fig. 2a, las curvas para g =10 y 100 μm se fusionan a frecuencias superiores a 0,05 THz, lo que sugiere que los modos de guía de ondas plasmónicas están tan estrechamente confinados en la interfaz BDS-aislante que la mayoría de los campos SPP se distribuyen dentro de la escala de 10 μm y la plata no funcionaría con un ancho de espacio tan grande. Mientras que el confinamiento de modo se mejora drásticamente después del ancho del espacio g se reduce gradualmente de 1 μm, el menor g investigaciones, y se puede obtener el confinamiento más fuerte. Se puede observar una tendencia similar en la dependencia de la pérdida de propagación del ancho de la brecha g , como se muestra en la Fig. 2b. Por otro lado, para un ancho de espacio fijo menor de 1 μm, Re ( n ef ) cada uno muestra inicialmente una reducción pronunciada al mínimo y luego exhibe un comportamiento que aumenta gradualmente, mientras que Im ( n ef ) cada uno disminuye monótonamente a medida que aumenta la frecuencia. Por lo tanto, existe una región de frecuencia optimizada en la que el confinamiento de modo se mejora fuertemente mientras que la pérdida de propagación se reduce gradualmente. Esta característica rara vez se ha observado en los modos tradicionales de guía de ondas plasmónicas en la interfaz metal-aislante. La Figura 2c, d representa la dependencia del confinamiento del modo y la pérdida de propagación de la energía de Fermi E F de la película BDS, donde el ancho del espacio g =1 μm. Al igual que en el caso de una guía de ondas monocapa y de doble capa, el confinamiento de modo y la pérdida de propagación disminuyen continuamente con el aumento de la energía de Fermi, lo que puede atribuirse a la metalicidad mejorada y al tiempo prolongado de relajación del portador de BDS. Por ejemplo, el factor de confinamiento del modo de guía de onda plasmónica a 2,5 THz puede ser de hasta λ 0 / 15, donde es λ 0 la longitud de onda incidente, con una pérdida relativamente baja de 1.0 dB / λ 0 cuando el ancho de la brecha de BDS-metal es de 10 nm y la energía de Fermi es de 70 meV. Por lo tanto, confiar en los marcos que ya se han discutido anteriormente aumentaría el confinamiento de modo con una pérdida relativamente baja, que se puede utilizar para el diseño de filtros ópticos integrados, amortiguadores e interferómetro Mach-Zehnder.
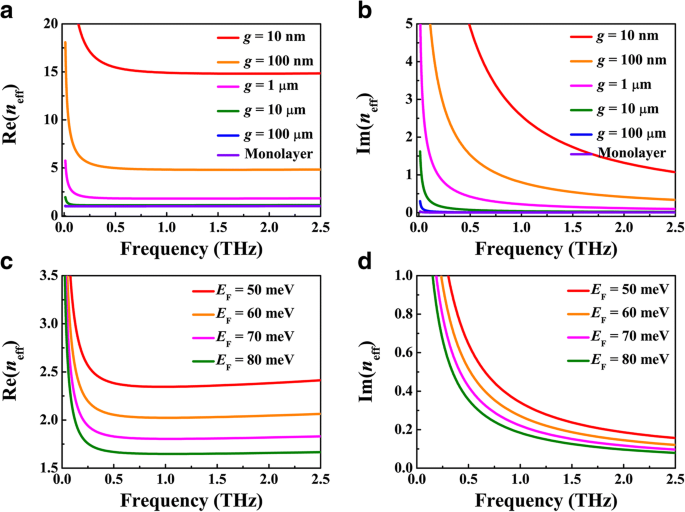
Partes reales e imaginarias del índice de refracción efectivo n ef para un , b diferente ancho de espacio g , donde la energía de Fermi de BDS se fija en E F =70 meV y c , d diferentes valores de la energía Fermi E F , donde el ancho del espacio se fija en g = 1 μm
Para examinar el análisis mencionado anteriormente, realizamos cálculos numéricos sobre la intensidad de transmisión y la distribución de campo de la estructura de guía de ondas propuesta. La configuración de la simulación se describe en métodos. Comparando con la guía de ondas BDS monocapa con la misma energía Fermi E F =70 meV, la intensidad de transmisión de la guía de ondas BIM a la frecuencia de 1,56 THz es 0,97, que es más alta que la de la primera, como se muestra en la Fig.3a, lo que sugiere que el modo de guía de ondas plasmónica en la estructura BIM sufre una menor pérdida de propagación. Por otro lado, como se indica en la Fig. 2a, la parte real del índice de refracción efectivo de BIM a 1,56 THz Re ( n ef ) =2,45, que es mucho más alto que el caso de la monocapa de 1,002. Para visualizar esta afirmación, el campo magnético Hz Las distribuciones de estos modos se presentan en la Fig. 3b, c. Se puede encontrar claramente que el modo plasmónico altamente confinado en la guía de ondas BIM muestra un período de oscilación más corto que el del caso BDS monocapa. Además, la mayor parte del campo plasmónico se localiza en una rendija tan estrecha ~ λ 0 / 2000, que tiene aplicaciones prometedoras en la mejora de campo cercano para la física no lineal.
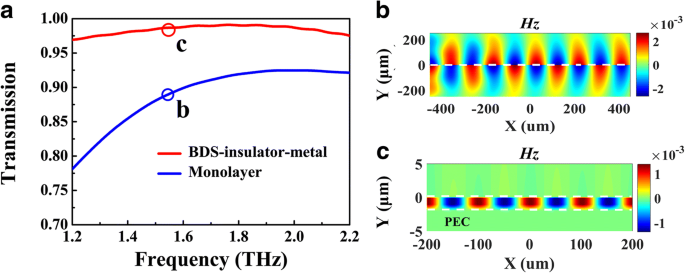
Cálculos numéricos de los espectros de transmisión ( a ) y campo magnético ( H z ) distribuciones ( b , c ) de guías de onda BIM (curva roja) y monocapa (curva azul), donde E F =70 meV, g =50 μ my frecuencia incidente de 1,56 THz
Entre todas las aplicaciones mencionadas anteriormente, el resonador óptico es el elemento esencial para adaptar el modo de guía de onda plasmónica THz. Como se ilustra en la Fig. 4a, dos silicio ( n Si =3.4) [24] cintas se incrustan en el espaciador dieléctrico para formar los espejos reflectantes, donde la onda plasmónica que se propaga se puede reflejar hacia adelante y hacia atrás en la interfaz silicio-aire formando una resonancia de onda estacionaria localizada en la región BIM entre las dos cintas de silicio . Solo la frecuencia incidente satisface la condición de resonancia de la onda estacionaria, las ondas plasmónicas pueden transmitirse a la salida de la guía de ondas mediante el acoplamiento con el resonador óptico diseñado. La Figura 4a presenta el espectro de transmisión de la guía de ondas BIM con dos cintas de silicio, donde se pueden encontrar dos picos de transmisión con valores FWHM (ancho completo a la mitad del máximo) de 0.12 y 0.09 THz a la frecuencia de 1.56 y 2.22 THz, lo que demuestra lo novedoso Efecto de filtrado de paso de banda en la región de terahercios. Las distribuciones del campo magnético (| H z | 2 ) de los picos de transmisión se muestran en la Fig. 4c, e, lo que implica que la región BIM intercalada por dos cintas de silicio se puede considerar como una cavidad de Fabry-Perot (FP). La resonancia de primer y segundo orden se puede encontrar claramente en la cavidad FP. La onda plasmónica incidente cerca de la frecuencia de resonancia se puede acoplar a la cavidad FP y luego se transmite a través de la guía de ondas BIM, que genera el pico de transmisión en el espectro. Mientras que, para la región de frecuencia no resonante, la onda estacionaria no se puede formar y, por lo tanto, las ondas incidentes están prohibidas en el puerto izquierdo de la guía de ondas BIM, como se muestra en la Fig. 4d. Además, combinado con la relación de dispersión de la guía de ondas BIM, la intensidad de transmisión se puede calcular analíticamente mediante la teoría del modo acoplado (CMT) [17]:
$$ T \ left (\ omega \ right) =\ frac {\ kappa_w ^ 2} {{\ left (\ omega - {\ omega} _0 \ right)} ^ 2 - {\ left ({\ kappa} _w + { \ kappa} _i \ right)} ^ 2}, $$ (5)donde ω 0 es la frecuencia de resonancia de la cavidad FP, respectivamente. Aquí, κ w = ω 0 / (2 Q w ) y κ i = ω 0 / (2 Q i ) son tasas de desintegración relacionadas con la pérdida de acoplamiento de la guía de ondas y la pérdida intrínseca de la cavidad FP, respectivamente. El factor de calidad de pérdida total e intrínseca se puede estimar mediante Q t = ω 0 / FWHM y Q oi =- Re ( n ef ) / (2Im ( n ef )), respectivamente. Luego, el factor de calidad de pérdida de acoplamiento de la guía de ondas se puede obtener restando la pérdida intrínseca de la pérdida total, es decir, Q ei =Q oi Q ti / ( Q oi - Q ti ) [17]. Los resultados analíticos basados en CMT concuerdan bien con las simulaciones numéricas, como se muestra en la Fig. 4b.
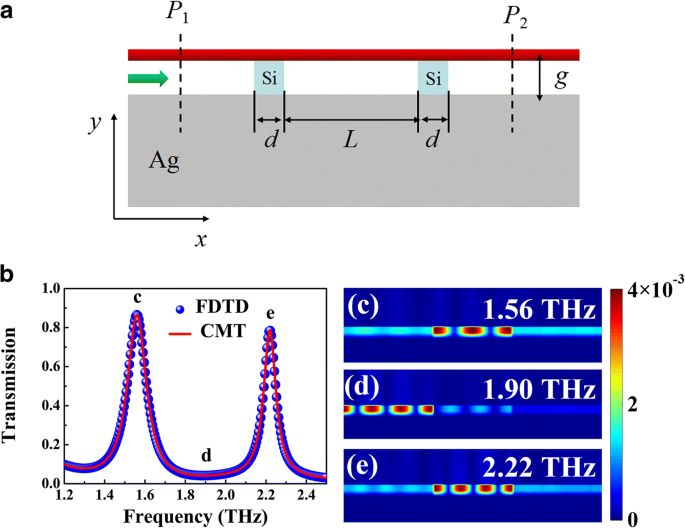
un Esquema de la guía de ondas BIM con cintas de silicona introducidas. El ancho de cada cinta de silicona es d , y la distancia entre las cintas es L . b Espectros de transmisión numéricos (bolas azules) y CMT ajustados (curva roja) de la estructura propuesta donde g =1 μm, d =5 μm y L =120 μm. c - e Distribuciones de campo magnético (| H z | 2 ) de en las frecuencias de incidentes de 1,56 ( c ), 1,90 ( d ) y 2,22 THz ( e )
La figura 5 muestra la dependencia de la frecuencia resonante de la longitud de la cavidad L , donde g =1 μm, d =5 μm y E F =70 meV. El pico de transmisión tiende a cambiar al rojo con el aumento de L , como se presenta en la Fig. 5a, que puede describirse con más detalle mediante la condición de resonancia de onda estacionaria 2 k SPP ( ω r ) L + θ =2 mπ ( m =1, 2, 3, ...), donde θ es el cambio de fase reflectante de la interfaz silicio-aire y k SPP ( ω r ) es el vector de onda de la guía de ondas BIM a una frecuencia resonante. Como se muestra en la Fig. 5b, las frecuencias de resonancia del primer y segundo modo de hecho exhiben un corrimiento hacia el rojo con el aumento de L . Según Eq. (1), el confinamiento del modo se ve afectado por el ancho del espacio g que por tanto tienen impacto en la frecuencia de resonancia. La Figura 6a presenta los espectros de transmisión para diferentes g , donde L =120 μm y E F =70 meV. Con el aumento de g , el pico resonante en el mismo orden exhibe un desplazamiento azul. Este fenómeno se puede atribuir a la dramática disminución de Re ( n ef ) como se muestra en la Fig. 6c. La sintonización de la energía de Fermi de BDS se puede realizar mediante el dopado superficial alcalino en el experimento. La Figura 6b presenta los espectros de transmisión para diferentes energías de Fermi, donde los otros parámetros son los mismos que en la Figura 4b. A medida que aumenta la energía de Fermi, el pico de transmisión presenta un cambio al azul, que también puede estar involucrado en la imagen de resonancia de la onda estacionaria. Para una longitud fija L , la cavidad FP soporta la resonancia con longitud de onda SPP definida λ SPP = λ 0 / Re ( n ef ), donde λ 0 es la longitud de onda incidente. Como se muestra en la Fig. 6c, Re ( n ef ) se reduce con el aumento de la energía de Fermi. Como resultado, la longitud de onda incidente λ 0 también debe reducirse para mantener λ SPP como una constante. Esa es la razón por la que el pico de transmisión tiende a cambiar al azul con el aumento de la energía de Fermi. Mientras tanto, el ancho de banda del pico de transmisión se reduce, lo que puede atribuirse a la disminución de Im ( n ef ), es decir, la pérdida de propagación del modo de guía de onda plasmónica en la guía de onda BIM.
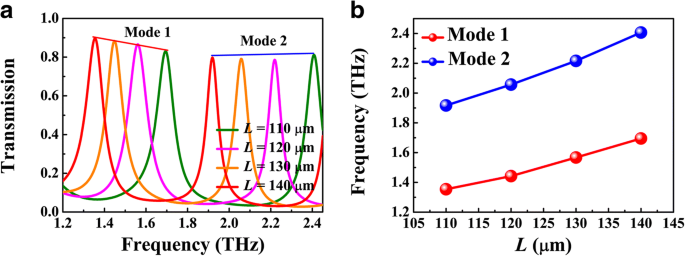
un Espectros de transmisión numérica para diferentes longitudes de cavidad L . b Frecuencias de resonancia de los modos 1 y 2 en función de la longitud de la cavidad L . Aquí, g =1 μm, d =5 μm y E F =70 meV
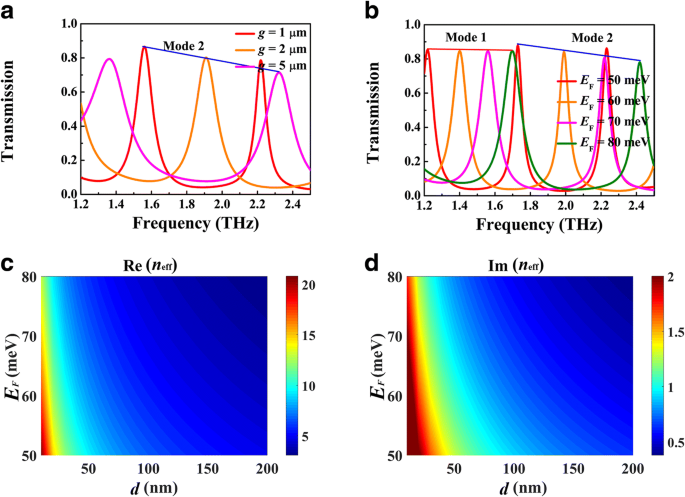
Espectros de transmisión para diferentes anchos de separación g ( a ) y Fermi energy E F ( b ), donde los demás parámetros son los mismos que en la Fig. 4b. Dependencia de Re ( n ef ) ( c ) y yo ( n ef ) ( d ) en Fermi Energy E F y ancho de espacio g
Conclusiones
En resumen, hemos demostrado el modo plasmónico de terahercios altamente confinado apoyado por una guía de ondas BIM. Las características de confinamiento y pérdida de modo se han discutido con las variaciones de la separación de BDS-metal y la energía de Fermi, lo que indica que hay un rango de frecuencia optimizado con confinamiento de modo mejorado, así como pérdida de propagación reducida, que rara vez se ha informado en el modo SPP tradicional. en estructura metálica. A diferencia de la estructura basada en BDS previamente estudiada, el modo de esta guía de ondas BIM se puede soportar de manera eficiente en una rendija muy estrecha con un ancho menor que λ 0 / 2000. Al tomar dos cintas de silicio como espejos reflectantes, se ha logrado un filtro de paso de banda dinámicamente sintonizable, donde la frecuencia resonante se puede controlar activamente ajustando la energía de Fermi de la película BDS sin volver a optimizar sus parámetros estructurales.
Métodos
Los resultados numéricos se obtienen utilizando el método 2D de dominio de tiempo de diferencia finita (FDTD), donde las capas perfectamente emparejadas se establecen para absorber la luz de dispersión en el x y y direcciones. El tamaño de malla de la película BDS se establece como d x × d y =1 μm × 0.02 μm para lograr una buena convergencia.
La conductividad dependiente de la frecuencia de BDS se describe mediante la fórmula de Kubo con aproximación de fase aleatoria [12, 25].
$$ \ operatorname {Re} \ sigma \ left (\ Omega \ right) =\ frac {e ^ 2} {\ mathrm {\ hslash}} \ frac {tk_F} {24 \ pi} \ Omega G \ left (\ Omega / 2 \ right), $$ (3) $$ \ operatorname {Im} \ sigma \ left (\ Omega \ right) =\ frac {e ^ 2} {\ mathrm {\ hslash}} \ frac {tk_F} {24 {\ pi} ^ 2} \ left \ {\ frac {4} {\ Omega} \ left [1+ \ frac {\ pi ^ 2} {3} {\ left (\ frac {T} {E_F} \ right)} ^ 2 \ right] +8 \ Omega {\ int} _0 ^ {\ varepsilon_c} \ left [\ frac {G \ left (\ varepsilon \ right) -G \ left (\ Omega / 2 \ right) } {\ Omega ^ 2-4 {\ varepsilon} ^ 2} \ right] \ varepsilon d \ varepsilon \ right \}, $$ (4)donde G ( E ) = n (- E ) - n ( E ) y n ( E ) es la función de distribución de Fermi-Dirac, E F es la energía Fermi de BDS, k F = E F / ћv F es su impulso de Fermi, y v F =10 6 m / s es la velocidad de Fermi. ε = E / E F , Ω = ћω / E F + iћτ −1 / E F , donde ћτ −1 = v F / ( k F μ ) es la tasa de dispersión de electrones que muestra una fuerte dependencia de la movilidad del portador μ. ε c = E c / E F ( E c es la energía de corte más allá de la cual el espectro de Dirac ya no es lineal), y t es el factor de degeneración cuántica. Tomando AlCuFe como ejemplo, los parámetros de ajuste en nuestros cálculos se establecen de la siguiente manera: t =40, ε c =3, μ = 3 × 10 4 cm 2 V −1 s −1 y E F =70 meV.
No hay participantes humanos, datos, tejidos o animales involucrados en esta investigación.
Abreviaturas
- BDS:
-
Semimetales de Dirac a granel
- BIM:
-
BDS-aislante-metal
- CMT:
-
Teoría del modo acoplado
- FDTD:
-
Dominio del tiempo de diferencia finita
- FWHM:
-
Ancho completo a la mitad del máximo
- SPP:
-
Polaritones de plasmón de superficie
Nanomateriales
- Introducción a la banda de terahercios
- Nanofibras y filamentos para una mejor administración de fármacos
- Nanobiosensor de oro basado en la resonancia de plasmón superficial localizado es capaz de diagnosticar la brucelosis humana, presentando un método rápido y asequible
- Dependencia de la resonancia de plasmón de superficie localizada del dímero de nanoprisma Ag truncado desalineado
- Propiedades infrarrojas y modulación de onda de terahercios de grafeno / ferrita MnZn / heterouniones p-Si
- Biocompatibilidad mejorada en matrices anódicas TaO x nanotubos
- Defectos en la superficie del nanofósforo de MgAl2O4 dopado con Ti
- Los efectos de acoplamiento de los polaritones de plasma superficial y las resonancias magnéticas dipolo en metamateriales
- Sensor plasmónico basado en nanoprismas dieléctricos
- Dispositivo bidimensional de haluro metálico híbrido que permite controlar las emisiones de terahercios
- Una nueva cámara flexible de terahercios puede inspeccionar objetos con diversas formas



