Dielectroforesis de ondas de frecuencia modulada de vesículas y células:cambios de sentido periódicos en la frecuencia de cruce

Resumen

Hemos formulado la fuerza dielectroforética ejercida sobre micro / nanopartículas tras la aplicación de campos eléctricos de frecuencia modulada (FM). Ajustando el rango de frecuencia de una onda FM para cubrir la frecuencia de cruce f _X en la parte real del factor de Clausius-Mossotti, nuestra teoría predice la inversión de la fuerza dielectroforética cada vez que la frecuencia instantánea atraviesa periódicamente f _X . De hecho, observamos giros en U periódicos de vesículas, células leucémicas y glóbulos rojos que se someten a dielectroforesis de ondas FM (FM-DEP). Nuestra teoría también sugiere que el seguimiento de video de los giros en U debido a FM-DEP está disponible para la medición ágil y precisa de f _X . El método FM-DEP requiere una duración corta, menos de 30 s, mientras se aplica la onda FM para observar varios giros en U, y la agilidad en la medición de f _X es de mucha utilidad no solo para suspensiones de células saladas sino también para nanopartículas porque el flujo de solvente inducido por el campo eléctrico se suprime tanto como sea posible. La precisión de f _X se ha verificado mediante dos tipos de experimentos. Primero, medimos la fuerza de atracción ejercida sobre una sola vesícula que experimenta dielectroforesis de corriente alterna (AC-DEP) a varias frecuencias de campos eléctricos sinusoidales. La dependencia de la frecuencia de la fuerza dielectroforética produce f _X como una frecuencia característica en la que la fuerza se desvanece. Comparando el resultado de AC-DEP de f _X con el obtenido del método FM-DEP, ambos resultados de f _X se encontró que coincidían entre sí. En segundo lugar, investigamos las dependencias de conductividad de f _X para tres tipos de celda cambiando los electrolitos circundantes. A partir de los resultados experimentales, evaluamos simultáneamente tanto las conductividades citoplasmáticas como las capacitancias de la membrana utilizando una teoría elaborada sobre el modelo de capa única de células biológicas. Si bien las conductividades citoplasmáticas, similares para estas células, fueron levemente más bajas que el rango de informes anteriores, las capacitancias de la membrana obtenidas estuvieron en buen acuerdo con las reportadas previamente en la literatura.

Antecedentes

La polarización de un fenotipo eléctrico se debe principalmente a la membrana celular y las propiedades eléctricas citoplasmáticas que dependen de la frecuencia del campo eléctrico aplicado. En consecuencia, las células individuales pueden identificarse por las diferencias en los espectros dieléctricos utilizando técnicas eléctricas no invasivas. Las técnicas eléctricas son actualmente competentes para separar células con fenotipos útiles de muestras desconocidas [1-15]. En comparación con otros métodos de separación, estos ofrecen la principal ventaja de que la modificación celular por anticuerpos o la adherencia a material extraño es innecesaria, por lo que se evita la posibilidad de daño celular o activación por estas sondas [1-16]. La caracterización de las propiedades dieléctricas celulares se ha realizado principalmente utilizando espectroscopia de impedancia [10, 12, 13] o electrocinética de corriente alterna (CA) como dielectroforesis (DEP), DEP de onda viajera (twDEP) y electrorrotación [1, 9, 15]. Entre ellos, nos enfocamos en extender el método AC-DEP para desarrollar un nuevo método de caracterización dieléctrica utilizando ondas de frecuencia modulada (FM) en lugar de campos de CA.

En general, la DEP ocurre en un gradiente de campo eléctrico que crea una fuerza electrocinética ejercida sobre cualquier objeto polarizable, cargado o neutro, en la dirección determinada no solo por el vector gradiente, sino también por la parte real de Clausius-Mossotti ( CM) factor [1-15, 17-21]. Por ejemplo, consideramos la fuerza DEP inducida por el campo eléctrico de CA E _AC ( r , t ) cuya dependencia espacio-temporal se expresa como E _AC ( r , t ) = A ( r ) porque θ _AC ( r , t ) usando el vector de amplitud A ( r ) y la fase θ _AC ( r , t ). La fuerza AC-DEP es generada por el gradiente espacial de la amplitud (es decir, ∇ A ) multiplicado por la parte real del factor CM, como se mencionó anteriormente, mientras que el gradiente espacial de la fase (es decir, ∇ θ _AC ) multiplicado por la parte imaginaria del factor CM crea la fuerza de twDEP o de electrorrotación, que por lo tanto proporciona información complementaria al método AC-DEP en términos de caracterización dieléctrica [9, 15, 20, 21].

En esta carta, nuestro objetivo es formular la fuerza DEP inducida por un campo FM y comparar los métodos AC- y FM-DEP, de modo que ni el campo AC ni el campo FM consideren la dependencia espacial de la fase; por lo tanto, configuraremos θ _AC ( t ) =2 π f _AC t en proporción a la frecuencia aplicada f _AC . Una característica importante del AC-DEP es que la dirección de la fuerza y su fuerza dependen de f _AC . En particular, la dirección de la fuerza se invierte en la frecuencia de cruce f _AC = f _X debido al cambio de signo de la parte real del factor CM, que se ha encontrado disponible para la caracterización dieléctrica utilizando AC-DEP [1-15].

La dependencia de la frecuencia de la fuerza AC-DEP también ha hecho posibles las siguientes manipulaciones [1-15, 22-31]:atrapamiento, enfoque y traslación eléctricamente controlables de partículas coloidales, así como el fraccionamiento y caracterización de seres vivos y / o células muertas. Los sistemas convencionales para el ensamblaje dielectroforético y / o la manipulación de partículas coloidales a menudo han hecho uso de electrodos microfabricados entre los cuales se ha aplicado el campo eléctrico de CA a suspensiones coloidales, beneficiándose de los rápidos avances recientes en la fabricación de dispositivos semiconductores integrados [24-30] . Esta tecnología, que ofrece manipulación sin contacto, se está integrando actualmente con una variedad de sistemas de laboratorio en un chip que brindan la ventaja de un manejo preciso y repetible. Sin embargo, los electrodos en el chip que crean puntos de alta intensidad en los campos de CA son incapaces de cambiar sus posiciones independientemente del soporte de la muestra, en contraste con el foco láser que se puede colocar libremente en la manipulación óptica. De la limitación de los sistemas en chip se deduce que los métodos DEP anteriores han presentado cierta dificultad y complejidad para realizar los tipos de operaciones para las que las pinzas ópticas son adecuadas. Un método candidato para superar estas dificultades es el DEP basado en imágenes ópticas [32].

Aquí, adoptamos, como una alternativa más simple, una de las técnicas de pinzas electrónicas [22, 23, 33-38] para el ensamblaje y / o manipulación dielectroforéticos bajo demanda sin un aparato óptico (ver Fig. 1). Como se ve en la Fig. 1, nuestro sistema de estilo enchufable utiliza un par de agujas de microelectrodos que están controladas por micromanipuladores para aplicar los campos eléctricos externos en una suspensión coloidal. Las sondas de los electrodos no eran fijas sino móviles en suspensiones coloidales debido a su estilo enchufable. Sin embargo, queda un requisito importante para el uso práctico de la caracterización dieléctrica:debe minimizarse la duración durante la cual se aplica un campo eléctrico a las celdas rodeadas de electrolitos salados. Por ejemplo, el método AC-DEP implica el uso de electrodos interdigitados en forma de peine que están incrustados en un sistema de microfluidos para que los campos de CA de varias frecuencias se puedan aplicar simultáneamente en una suspensión celular [24-30]. Si bien estos sistemas refinados en chip se han encontrado relevantes para la caracterización dieléctrica, la técnica de par de electrodos múltiples es inaplicable al sistema de par de electrodos únicos que se ha utilizado a menudo en las técnicas de pinzas electrónicas [22, 23, 33-38] .

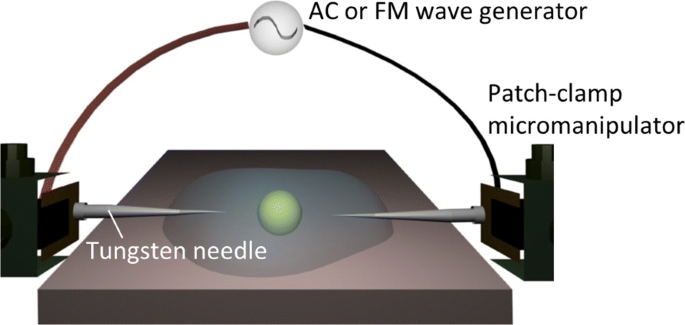
Configuración experimental. Un esquema del sistema de manipulación dielectroforética que ilustra el campo eléctrico de CA o FM aplicado a una partícula objetivo a través de un par de agujas de electrodo controladas por micromanipuladores de pinza de parche

Para lograr mediciones de multifrecuencia simultáneas utilizando el sistema de par de electrodos únicos (Fig. 1), se debe investigar el cambio en el campo eléctrico aplicado. En esta carta, abordamos la disponibilidad de DEP variable en el tiempo debido a una onda FM (FM-DEP) de la siguiente forma:

$$ \ boldsymbol {E} (\ boldsymbol {r}, t) =\ boldsymbol {A} (\ boldsymbol {r}) \ cos \ theta (t), $$ (1)

donde la fase θ ( t ) de la onda FM está relacionada con la frecuencia instantánea f ( t ) como 2 π f ( t ) = d θ ( t ) / d t y

$$ f (t) =f_ {c} + \ Delta f \ cos \ left (2 \ pi f_ {m} t \ right), $$ (2)

con f _m que denota la frecuencia de modulación. Usamos FM de banda ancha para satisfacer que Δ f / f _m ≫1, de modo que las condiciones de f _m / f ( t ), f _m / f _c , f _m / Δ f ≪1 se denominará límite de banda ancha (WBL) en la formulación teórica que se proporciona a continuación.

En esta carta, se presta especial atención a la relación entre la frecuencia característica de f _X y la trayectoria de FM-DEP. En la siguiente sección, describimos tanto los materiales utilizados como los detalles del sistema enchufable para inducir FM-DEP. La tercera sección proporciona los resultados y la discusión que consta de cuatro partes. Primero, investigamos los detalles de los giros en U repetidos de una sola célula leucémica cuantificando la trayectoria recíproca, cuya periodicidad se explica por la frecuencia de modulación f _m , o la oscilación periódica de f ( t ) dada por la Ec. (2). A continuación, explicamos teóricamente la trayectoria recíproca derivando la fuerza dielectroforética variable en el tiempo que modula de acuerdo con la frecuencia instantánea f ( t ) del campo FM que cumple la condición WBL. La forma obtenida de la fuerza dielectroforética proporciona la ecuación que determina la f _X de los giros en U observados. En tercer lugar, medimos la magnitud de la fuerza dielectroforética en una vesícula multilaminar (MLV) que se adjuntó a una aguja de electrodo debido a la atracción del AC-DEP. La dependencia de la frecuencia de la fuerza se ajustó utilizando la ecuación espectral que se determinó a partir de la parte real del factor CM, de modo que f _X se determinó como la frecuencia característica a la que desaparece la fuerza de atracción debida a AC-DEP. Debido a que el método FM-DEP también da f _X Al analizar la trayectoria recíproca de un MLV, evaluamos el grado de coincidencia entre las frecuencias de cruce evaluadas de AC- y FM-DEP. Finalmente, se evaluaron tanto las conductividades citoplasmáticas como las capacitancias de membrana de tres tipos de células a partir de f _X como una función creciente de la conductividad de la solución, y los valores obtenidos se compararon con los reportados en la literatura.

Métodos

Materiales

Para preparar vesículas multilaminares (MLV), utilizamos 1,2-dioleoil-sn-glicero-3-fosfatidilcolina (DOPC) como lípidos, adquiridos de Avanti Polar Lipids. Las MLV se obtuvieron mediante el siguiente procedimiento. El DOPC (1 mL, 20 mM) disuelto en cloroformo / metanol (2:1 v / v ) se secó con N ₂ gas, y el disolvente se eliminó completamente al vacío durante más de 12 h. La fina película depositada en el vial de vidrio debido a la evaporación se rehidrató con agua desionizada y se incubó a 25 ° C durante varias horas.

Dos líneas celulares utilizadas en los experimentos fueron JKT-beta-del de la línea de leucemia de células T humanas (TL) y CCRF-SB de la línea de leucemia de células B humanas (BL). Ambos tipos de células TL y BL se utilizaron después de 1 semana de incubación en una incubadora humidificada que contiene 5 % CO ₂ a 37, por lo que teníamos las concentraciones de células dentro del rango de 0.5 × 10 ⁶ a 1 × 10 ⁶ células / mL. El medio RPMI 1640 para el cultivo celular se complementó con suero de brovina fetal al 10% y piruvato de sodio 100 mM. Las células se sedimentaron mediante centrifugación a 370 g durante 3 min dos veces para que las células pudieran resuspenderse puramente en 1 ml del medio RPMI 1640 antes del pipeteado. Las suspensiones de células obtenidas se diluyeron adicionalmente usando la solución isotónica de sacarosa 200 mM para prepararse para que el solvente tenga la conductividad requerida.

También usamos células de sangre roja humana (RB) dispersas en las siguientes suspensiones. Se obtuvieron muestras de sangre entera recién extraídas de voluntarios sanos de poco más de veinte años. Las células, suspendidas en una mezcla del medio RPMI 1640 y un hematocrito del 3,1%, se diluyeron usando la solución isotónica de sacarosa 200 mM para preparar el disolvente que tiene la conductividad requerida así como las células de leucemia anteriores. Todos los experimentos dielectroforéticos con células RB humanas se terminaron dentro de los 10 minutos posteriores a la extracción de las muestras de sangre completa.

Configuración experimental

Las conductividades de las suspensiones celulares se midieron usando un conductímetro (SevenMulti, Mettler-Toledo, Columbus, OH, EE. UU.). En la Fig. 1 se muestra un esquema del sistema enchufable utilizado. Se aplicó un campo eléctrico externo con una onda de CA o FM a través de un generador de forma de onda arbitraria (Agilent 33220A, Agilent Technologies, Santa Clara, CA, EE. UU.) Con una corriente amplificador (F30PV, FLC Electronics, Partille, Suecia) al que se conectaron microelectrodos enchufables. Los microelectrodos comprendían agujas de tungsteno con un diámetro de punta de 0,5 μ m que fueron controlados de forma independiente por dos juegos de micromanipuladores de pinza de parche (NMN-21, Narishige, Setagaya-ku, Tokio, Japón). En todos los experimentos que siguen, mantuvimos la separación de la punta en 100 μ m al aplicar los campos externos a las suspensiones anteriores, y la magnitud máxima se estableció en 0,5 kV / cm. El par de agujas se insertó en una gota de muestra montada en el microscopio óptico invertido (TE2000-U, Nikon, Minato-ku, Tokio, Japón), y las micrografías ópticas se obtuvieron usando una cámara CCD (Retiga Exi, QImaging, Surrey, British Columbia, Canadá) con una velocidad de fotogramas de 25 fps; de paso, se confirmó que la resolución de frecuencia de las ondas FM debido a la velocidad de cuadros siempre estuvo dentro de las barras de error para cada dato. 50- μ Se montó una gota de suspensión en la platina de muestra del microscopio óptico invertido, cuya temperatura se mantuvo a 25 ° C mediante un controlador de calor.

La técnica de plug-in permite que el sistema simple realice varias manipulaciones sin contacto de una sola celda, como empujarla hacia un canal estrecho sin ningún contacto y orientarla hacia la dirección deseada. Aunque a menudo es necesario tratar las células en una solución isotónica con sal, es más fácil implementar las manipulaciones de DEP anteriores de las células rodeadas de agua desionizada. En el archivo adicional 1:Películas S1 a S3, el sistema enchufable indujo el AC-DEP de las células de diatomeas suspendidas en agua desionizada. Podemos ver en el archivo adicional 1:Películas S1 a S3 que una celda de diatomea anisotrópica dispersa en agua sin sal fue manipulada como una etiqueta post-it por un par de microelectrodos entre los cuales se aplicó el campo eléctrico de CA (1 kV / cm) . Las operaciones sin contacto constan de tres pasos:(i) primero se rotó una celda objetivo en paralelo a una pared de vidrio cargada positivamente mediante la combinación de alineación de dipolos a una frecuencia de 30 kHz y cambio de posición de cada microelectrodo (archivo adicional 1:Película S1 ), (ii) posteriormente cambiamos la frecuencia a 100 kHz para empujarla hacia la pared para fijar electrostáticamente la celda de solicitud con cargas negativas en la superficie del vidrio (Archivo adicional 1:Película S2), y (iii) se ajustó la frecuencia de CA a 20 MHz para inducir el AC-DEP en la dirección opuesta, de modo que la celda unida electrostáticamente pueda extraerse (Archivo adicional 1:Película S3).

Resultados y discusión

Observación experimental de una célula leucémica que experimenta FM-DEP

Nuestros microelectrodos enchufables (ver Fig. 1) permiten que el campo eléctrico se aplique a las partículas que flotan muy por encima del sustrato de muestra, lo cual es de uso práctico para seleccionar las celdas apropiadas. Por ejemplo, Archivo adicional 1:Película S4 muestra que el par de microelectrodos se controló para acercarse a una celda de diatomea triangular flotante a la que aplicamos el campo eléctrico de CA con su frecuencia saltando entre 100 y 500 kHz a intervalos de 0,5 s. En el archivo adicional 1:Película S4, vemos la celda triangular rebotando en un microelectrodo debido al salto de frecuencia como resultado preliminar antes de la siguiente manipulación usando el FM-DEP.

Archivo adicional 1:Las películas S5 y S6 muestran los comportamientos típicos de varias células TL que experimentan FM-DEP, que son similares a las de las células de mamíferos manipuladas por pinzas electrónicas utilizando un solo electrodo AC-DEP [36]. La Figura 2 muestra una de las trayectorias periódicas usando la gráfica 3D de ( x , años ) a lo largo de la t eje, donde una coordenada relativa de ( x , años ) se asigna a la posición de celda temporal con el origen de (0, 0) ubicado en un punto específico en una aguja de microelectrodo para extraer la configuración celda-electrodo. Mientras que el x El eje representa la tangente a la superficie del electrodo en (0, 0), la y El eje, perpendicular a la tangente, refleja principalmente la proyección de los giros en U periódicos que se explican a continuación. En la Fig.2, seleccionamos una celda TL flotante a la que aplicamos el campo eléctrico FM con su frecuencia de modulación f _m configurado para ser f _m =0,25 Hz en el rango de 200 kHz ≤ f ( t ) ≤ 3 MHz. Porque tenemos ese Δ f / f _m , f ( t ) / f _m <10 ⁻⁵ , la condición WBL realmente se mantiene, como se menciona después de la Ec. (2).

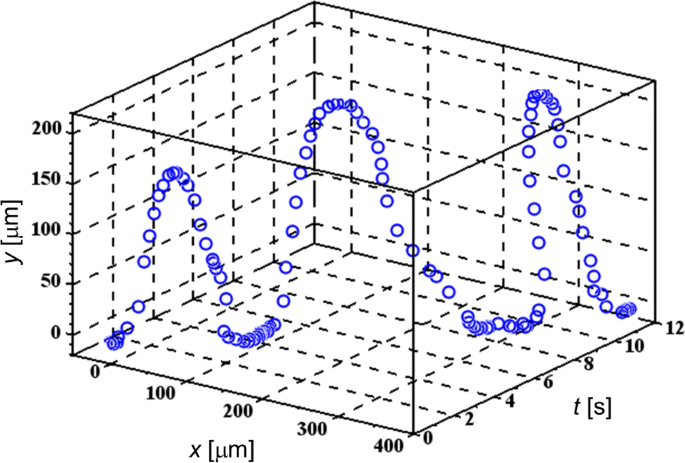
Trayectoria 3D de una celda TL dirigida. Se demuestran giros en U periódicos debido a la modulación de frecuencia para la celda TL que se somete a FM-DEP

Se encuentra en el archivo adicional 1:Películas S5 y S6, así como en la Fig.2, que la trayectoria periódica está constituida por tres partes de salir, acercarse y permanecer en el microelectrodo:(i) la celda deja el microelectrodo, (ii) se acerca al microelectrodo después de hacer un giro en U, y (iii) permanece en la superficie del microelectrodo. La celda a menudo no puede regresar a la misma posición en la superficie del microelectrodo debido al flujo de solvente, que no solo se observa en el archivo adicional 1:Película S6, sino que también está representado por los giros en U con la celda migrando en el x dirección en la Fig. 2. A pesar de la interferencia con el flujo de solvente, es posible distinguir los momentos en que la celda comienza a salir de la superficie del microelectrodo y hace el giro en U en la trayectoria periódica, respectivamente. En consecuencia, podemos ver en la Fig.2 que estos giros en U se repiten a intervalos de 4 s en coincidencia con la frecuencia de modulación de 0.25 Hz, o el período de 4 s de la frecuencia instantánea f ( t ).

Estudio teórico sobre el FM-DEP

Para explicar las trayectorias experimentales, incluidos los giros en U periódicos, consideramos un objeto esférico como un modelo simplificado de una sola celda, a la que un campo eléctrico arbitrario variable en el tiempo E ( r , t ) Está aplicado. La Figura 3 muestra un esquema de la fuerza DEP dependiente del tiempo que actúa sobre un objeto esférico [9]. Como se muestra en la Fig.3, la permitividad y la conductividad dentro de un objeto esférico están representadas por ε _en y σ _en , respectivamente, y el subíndice "out", como ε _fuera y σ _fuera , denota el exterior. En general, F _DEP ( r , t ) está relacionado con el momento dipolar inducido p ( r , t ) como [17-19]

$$ \ begin {array} {@ {} rcl @ {}} \ boldsymbol {F} _ {\ text {DEP}} (\ boldsymbol {r}, t) &=&\ left \ {\ boldsymbol {p} (\ boldsymbol {r}, t) \ cdot \ nabla \ right \} \ boldsymbol {E} (\ boldsymbol {r}, t), \ end {matriz} $$ (3)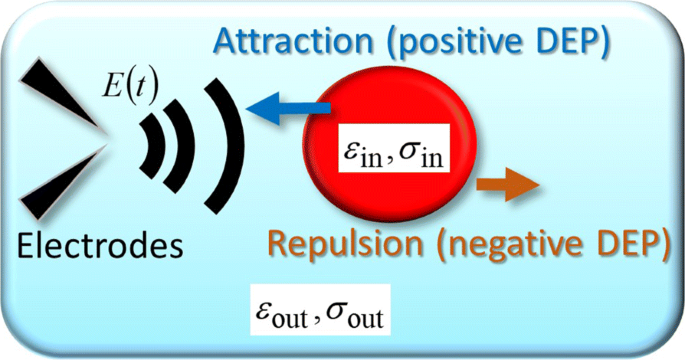

Modelo teórico. Representación esquemática de la fuerza FM-DEP ejercida sobre una celda que se modela como un modelo de esfera homogénea que tiene la permitividad y conductividad de ε _en y σ _en , respectivamente. La esfera está rodeada por medio electrolítico con su permitividad y conductividad de ε _fuera y σ _fuera , respectivamente. El modelo de esfera homogénea es la simplificación del modelo de capa única esférica que considera a la célula como un citoplasma extendido rodeado por una membrana [9]

$$ \ begin {array} {@ {} rcl @ {}} \ boldsymbol {p} (\ boldsymbol {r}, t) &=&4 \ pi R ^ {3} \ epsilon _ {\ text {out}} K_ {H} \ left \ {\ boldsymbol {E} (\ boldsymbol {r}, t) + \ frac {\ tau} {\ Delta \ tau} \ widetilde {\ boldsymbol {E}} (\ boldsymbol {r}, t) \ right \}, \ end {matriz} $$ (4) $$ \ begin {matriz} {@ {} rcl @ {}} \ widetilde {\ boldsymbol {E}} (\ boldsymbol {r}, t ) &=&\ frac {1} {\ tau} \ int_ {0} ^ {tds} \, \ boldsymbol {E} (\ boldsymbol {r}, ts) e ^ {- s / \ tau}, \ end {array} $$ (5)

donde K _H y Δ τ se definen de la siguiente manera: K _H =( ε _en - ε _fuera ) / ( ε _en +2 ε _fuera ) y \ (\ Delta \ tau ^ {- 1} =\ tau _ {0} ^ {- 1} - \ tau ^ {- 1} \) usando el radio R del objeto esférico y dos tiempos característicos de τ ₀ =( ε _en - ε _fuera ) / ( σ _en - σ _fuera ) y τ =( ε _en +2 ε _fuera ) / ( σ _en +2 σ _fuera ).

Sustituyendo el campo eléctrico de CA E _AC ( r , t ) = A ( r ) cos (2 π f _AC t ) en Ecs. (3) a (5), obtenemos la fuerza DEP media < F _DEP ( r , t )> que se ha promediado a lo largo de los ciclos del campo AC [9, 15, 20]:

$$ \ begin {array} {@ {} rcl @ {}} \ left <\ boldsymbol {F} _ {\ text {DEP}} \ right> &=&4 \ pi R ^ {3} \ epsilon _ {\ text {out}} K_ {H} \ left [\ left <\ boldsymbol {E} \ cdot \ nabla \ boldsymbol {E} \ right> + \ frac {\ tau} {\ Delta \ tau} \ left <\ widetilde { \ boldsymbol {E}} \ cdot \ nabla \ boldsymbol {E} \ right> \ right] \\ &=&\ chi (f _ {\ text {AC}}) \ nabla \ boldsymbol {A} ^ {2} _ {\ text {RMS}}, \ end {matriz} $$ (6)

donde A _RMS denota el vector de raíz cuadrada media (RMS) que satisface que \ (\ boldsymbol {A} _ {\ text {RMS}} ^ {2} =\ boldsymbol {A} ^ {2} / 2 \), y χ ( f _AC ) ≡2 π R ³ ε _fuera Re [ K ( f _AC )] depende de la frecuencia aplicada f _AC debido a Re [ K ( f _AC )], la parte real del factor CM [9, 15, 20]:

$$ \ begin {array} {@ {} rcl @ {}} \ chi (f _ {\ text {AC}}) =\ frac {2 \ pi R ^ {3} \ epsilon _ {\ text {out}}} {1+ (2 \ pi f _ {\ text {AC}} \ tau) ^ {2}} \ left \ {K_ {L} + (2 \ pi f _ {\ text {AC}} \ tau) ^ {2 } K_ {H} \ right \}, \ end {array} $$ (7)

donde K _L =( σ _en - σ _fuera ) / ( σ _en +2 σ _fuera ) y K _H , definidos anteriormente, corresponden a los valores reales de CM en los límites de baja y alta frecuencia, respectivamente, y estos valores límite, K _L y K _H , debe tener signos opuestos para que f _X definido por χ ( f _X ) =0 puede existir [9, 15, 20].

Las ecuaciones (6) y (7) indican que el campo eléctrico de CA crea la fuerza DEP cuya dirección depende de la frecuencia aplicada f _AC hasta χ ( f _AC ) dada por la Ec. (7), que explica la celda de diatomea que rebota en el archivo adicional 1:Película S4 de la siguiente manera (consulte también la Fig. 3). Cuando la frecuencia aplicada proporciona el signo más de la parte real del factor CM (es decir, χ ( f _AC )> 0), podemos observar células atraídas hacia las puntas de las agujas de los electrodos (el DEP positivo) en las que la fuerza del campo de CA, aplicada a través de un par de agujas de los electrodos, es la mayor. El signo del factor CM real se puede invertir al negativo en f _X , la frecuencia de desaparición del factor CM real (es decir, χ ( f _X ) =0), donde tenemos la fuerza dielectroforética cero como se encuentra en la Ec. (6). En el signo negativo del factor CM (es decir, χ ( f _AC ) <0), los coloides individuales son repelidos del par de agujas del electrodo (el DEP negativo). La celda de diatomea triangular en el archivo adicional 1:Película S2 rebotó debido a la dirección opuesta de los AC-DEP inducidos por los campos de CA con sus frecuencias de 100 y 500 kHz; combinando Eq. (6) y las direcciones dielectroforéticas observadas, encontramos que χ (100 kHz)> 0 y χ (500 kHz) <0.

A continuación, consideramos el FM-DEP conectando la fase dada por las Ecs. (1) y (2) en las ecuaciones. (3) a (5). Como se demuestra en el archivo adicional 2, la condición WBL de la onda FM valida la forma aproximada de la integración en la ecuación. (5), proporcionando así

$$ \ left <\ widetilde {\ boldsymbol {E}} \ cdot \ nabla \ boldsymbol {E} \ right> =\ frac {1} {1 + \ {2 \ pi f (t) \ tau \} ^ { 2}} \ left (\ frac {\ nabla \ boldsymbol {A} ^ {2} _ {\ text {RMS}}} {2} \ right), $$ (8)

que se convierte en la misma forma que la del AC-DEP cuando la frecuencia dependiente del tiempo f ( t ) se reemplaza por una frecuencia constante de f _AC . De este modo obtenemos la forma límite de la fuerza DEP media < F _DEP ( r , t )> que se ha promediado durante ciclos de θ ( t ) en el campo FM (consulte las ecuaciones (A1), (A13) y (A14) en el archivo adicional 2):

$$ \ begin {array} {@ {} rcl @ {}} \ left <\ boldsymbol {F} _ {\ text {DEP}} (\ boldsymbol {r}, t) \ right> =\ chi \ {f (t) \} \ nabla \ boldsymbol {A} ^ {2} _ {\ text {RMS}}, \ end {matriz} $$ (9)

siendo de una forma similar a la Eq. (6) para el AC-DEP. La diferencia es si el coeficiente de χ { f ( t )} depende de t hasta f ( t ), que cambia cíclicamente según la modulación de frecuencia con el período de T _m =1 / f _m .

Con base en la expresión simple (9) del FM-DEP, ilustramos con la Fig. 4 el mecanismo de los giros en U anteriores debido a la onda FM. La Figura 4 muestra un esquema de la DEP inducida por la onda FM en el WBL cuando el rango de f ( t ) cubre la frecuencia de cruce f _X tal que f _c - Δ f ≤ f _X ≤ f _c + Δ f . En la Fig.4 se supone que la dependencia de la frecuencia de la parte real del factor CM, o χ { f ( t )}, proporciona los cambios de signo alternativos de la siguiente manera:signo menos ( χ { f ( t )} <0) para f ( t ) < f _X y el signo más ( χ { f ( t )}> 0) para f ( t )> f _X , que es el caso de nuestros experimentos. El período anterior satisfacía f ( t ) < f _X tiene un tiempo de duración, mientras que el último f ( t )> f _X se ha retenido durante el resto del período:un ciclo se clasifica en dos períodos que están marcados en rojo y azul, respectivamente, en la Fig. 4.

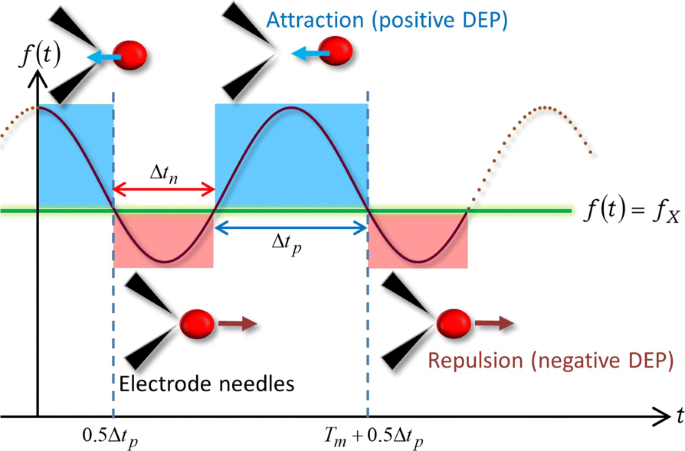
Dirección de fuerza relacionada con la modulación de frecuencia. Una ilustración de los giros en U periódicos debidos a la onda FM con su frecuencia dependiente del tiempo de f ( t ) cubriendo una frecuencia de cruce f _X

De manera similar al AC-DEP, Eq. (9) implica que el signo menos ( χ { f ( t )} <0) crea una fuerza DEP repulsiva entre la celda y los microelectrodos mientras satisface que f ( t ) < f _X . Como resultado, la celda abandona el área alrededor de las puntas de las agujas del microelectrodo entre las cuales la magnitud del campo eléctrico es mayor:la celda experimenta la DEP negativa durante el período rojo de Δ t _n en la Fig. 4. En el instante t _X como una solución de f ( t _X ) = f _X , χ ( f ) desaparece, seguido del cambio de signo a χ ( f )> 0 mientras f ( t )> f _X y, en consecuencia, la fuerza DEP se cambia a la fuerza de atracción en t _X . Después de hacer un cambio de sentido en t _X Debido a la inversión en la dirección de la fuerza DEP, la celda objetivo comienza a acercarse al microelectrodo migrando en la dirección opuesta y finalmente queda atrapada entre las puntas de las agujas del electrodo o adherida a uno de los electrodos:la celda experimenta la DEP positiva durante el período azul de Δ t _p en la Fig. 4. La Figura 4 indica que el ciclo de salir, acercarse y permanecer en el microelectrodo debe repetirse con el período de modulación de T _m , de acuerdo con la Fig.2: Δ t _n + Δ t _p = T _m . El mecanismo dielectroforético representado en la Fig. 4 puede explicar los giros en U periódicos observados en el archivo adicional 1:Películas S5 y S6, así como en la Fig. 2.

Consideremos la solución periódica de la ecuación, f ( t _X ) = f _X . Como se ve en la Fig. 4, t _X se expresa como t _X = n T _m +0,5 Δ t _p = n T _m +0,5 ( T _m - Δ t _n ) usando un número entero de n =0, ± 1, ± 2, ⋯, que dice además

$$ 2 \ pi f_ {m} t_ {X} =(2n + 1) \ pi- \ pi f_ {m} \ Delta t_ {n}. $$ (10)

Sustituyendo la ecuación. (10) en la ecuación. (2), tenemos para n =0 que

$$ f_ {X} =f_ {c} - \ Delta f \ cos \ left (\ pi f_ {m} \ Delta t_ {n} \ right), $$ (11)

aclarando que el método FM-DEP determina la frecuencia de cruce si el tiempo de duración Δ t _n from leaving the microelectrode to doing the U-turn can be measured precisely.

Comparing Crossover Frequencies of a Single MLV Determined from the FM- and AC-DEPs

We investigated the experimental accuracy of Eq. (11). Experimentally, it is often necessary for the biological cells to be dispersed in an electrolyte. For MLVs, however, the use of deionized water is allowed during the preparation process of rehydration and dilution. We thus used the salt-free MLV suspension for comparing the crossover frequencies determined from both AC- and FM-DEPs.

The dielectrophoretic U-turns of a targeted MLV were induced by the FM wave in the range of 10 kHz ≤f (t )≤ 50 kHz (i.e., f _c =30 kHz and Δ f =20 kHz) with a setting that f _m =0.1 Hz, and correspondingly the FM-DEP has a 10-s period. In the experiments, it takes less than 30 s to observe a few U-turns of the targeted MLV from leaving to approaching microelectrodes. From the trajectory, we obtained the mean leaving time that $\overline {\Delta t_{n}}=5.8\pm 0.2$ s. Because the WBL condition applies to the present experiment satisfying that f _m /Δ f /f _m , f _, m /f (t )<10⁻⁵ , the crossover frequency was evaluated to be f _X =35±1 kHz from substituting $\overline {\Delta t_{n}}=5.8\pm 0.2$ s into Eq. (11).

For comparison, we made use of the programmable manipulator in the AC-DEP method that tries to evaluate the crossover frequency of the same targeted MLV to which the sinusoidal electric field with a frequency in the range of 30 to 100 kHz was applied via the electrode needle pair for inducing the AC-DEP. Because the programmable manipulator carries the electrode needle pair at a constant speed in one direction, we can measure the dielectrophoretic force similarly to the laser-trapping experiments [39]. Attaching the MLV on an electrode tip that undergoes uniform linear motion, not only the AC-DEP force but also the hydrodynamic force caused by the one-dimensional motion are exerted on the MLV. With the gradual increase of electrode velocity, F _DEP eventually becomes smaller than the hydrodynamic force. As a result, the MLV initially attached to the moving electrode, owing to the DEP attraction, is desorbed by the hydrodynamic force. Defining the critical value, v _c , by the maximum velocity value of the microelectrode pair prior to the desorption, the force balance equation between the DEP and hydrodynamic forces reads [39]

$$ F_{\text{DEP}}(f_{\text{AC}})=6\pi\eta R v_{c}, $$ (12)

where F _DEP (f _AC )e ≡<F _DEP> with the unit vector e defined by $\boldsymbol {e}=\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}/|\nabla {\boldsymbol {A}}^{2}_{\text {RMS}}|$, η the water viscosity at 25 °C and 2R the diameter of the MLV.

Additional file 1:Movies S7 and S8 demonstrates the force measurement using the above AC-DEP method at the applied frequency of f _AC =60 kHz. In Additional file 1:Movie S7, the velocity of the electrode pair controlled by the programmed manipulator is 110 μ m/s, which is lower than v _c; therefore, the MLV remains attached to one part of the electrode pair owing to the dielectrophoretic attraction. Additional file 1:Movie S8, on the other hand, shows the higher electrode speed of 120 μ m/s, under which the dielectrophoretic force becomes smaller than the hydrodynamic force that is exerted on the MLV, thereby desorbing the MLV from the electrode. Accordingly, v _c is evaluated to be 110 μ m/s ≤v _c ≤ 120 μ m/s, and we can calculate F _DEP (60 kHz) using Eq. (12).

We can determine f _X from the experimental results of F _DEP at various external frequencies. Figure 5 shows the frequency dependence of F _DEP , indicating that the DEP force experienced by the MLVs was reduced by lowering the applied frequency. It is found from Eqs. (6) and (7) that the fitting function of F _DEP (f _AC ) can be expressed as

$$ F_{\text{DEP}}(f_{\text{AC}})=\frac{L+(2\pi f_{\text{AC}}\tau)^{2}H}{1+(2\pi f_{\text{AC}}\tau)^{2}}, $$ (13)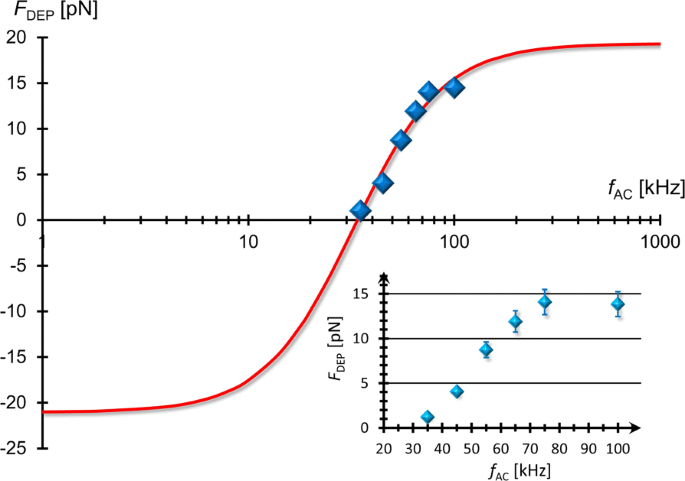

Frequency dependence of F _DEP . The FM-DEP force (F _DEP ) as a function of external frequency (f _AC ) of applied AC field where F _DEP has been evaluated from Eq. (12), the balance equation between the FM-DEP and hydrodynamic forces exerted on a single MLV. It can be seen that F _DEP is increased and saturated as f _AC is higher, reflecting a typical behavior of the relaxation spectrum of the real CM factor. The solid line represents the best-fit result of Eq. (13)

implying that

$$ f_{X}=\frac{1}{2\pi\tau}\sqrt{-\frac{L}{H}}. $$ (14)

Equation (13) is depicted by the solid line in Fig. 5 that has been fitted to the experimental data using the best-fit results of three parameters:L =−21.02 pN, H =19.03 pN, and τ =4.9 μ s. Substituting these results into Eq. (14), we evaluate that f _X =34.15 kHz, which coincides with the result of f _X =35±1 kHz evaluated from the FM-DEP method. The FM-DEP method is thus validated in terms of the consistency with the direct force measurement using the AC-DEP method.

Conductivity Dependencies of the Crossover Frequencies for Biological Cells

Let us return to the dielectrophoretic U-turns of biological cells mentioned in Fig. 2 to assess the practical reliability of the crossover frequencies when the FM-DEP method is applied to cell suspensions. Recently, an elaborate theory [40] has investigated, in more detail than before, the relationship between the homogeneous sphere model (see Fig. 3) and the single-shell model where the inner structure of cell is represented by a smeared-out cytoplasm surrounded by a membrane. As a result, the relation between f _X and the suspension conductivity σ _out has been formulated using radius R of a cell, membrane capacitance C _m , and cytoplasmic conductivity σ _cyt [40]:

$$ f_{X}=\frac{1}{\sqrt{2}\pi {RC}_{m}}\left(\sigma_{\text{out}}-\frac{1}{2\sigma_{\text{cyt}}} \sigma_{\text{out}}^{2} \right)+f_{X0}, $$ (15)

where f _{X 0} is the extrapolated value to the crossover frequency at σ =0 mS/m and will be treated as a fitting parameter herein. The elaborate treatment adds the squared term, the second term on the right hand side of Eq. (15), to the conventional linear relation which has mainly been used for evaluating C _m from f _X [40–45]. Theoretically, it has still been claimed [40] that Eq. (15) is valid within a lower range of σ _out such that σ _out <10 mS/m; however, it should be better to include the squared term in the evaluation of C _m , considering that our range of σ _out is relatively high compared with previous results in the range of 10 mS/m ≤σ _out ≤ 100 mS/m [40–45]. Hence, we determined σ _cyt as well as C _m from fitting Eq. (15) to the experimental results of f _X as an increasing function of σ _out .

There are three kinds of biological cell used:TL and BL cells of human leukemia and RB cells of three human volunteers. In all the experiments using any species of cell, the conductivities were within the range of 60 to 160 mS/m, and the modulation frequency was set to be 0.25 Hz. Regarding the instantaneous frequency, most of the experiments adopted the range from 100 to 1.5 MHz (i.e., f _c =800 kHz and Δ f =700 kHz); exceptionally for leukemia cells, the frequency range was extended to 50 kHz ≤f (t )≤1550 kHz (i.e., f _c =800 kHz and Δ f X =750 kHz) in the conductivity range of 60 mS/m≤σ ≤80 mS/cm because f _X in this σ -range has been found to be lower than 100 kHz, and we were unable to observe the DEP U-turns in the range of 100 kHz ≤f (t )≤1500 kHz. Both of these frequency sets satisfy the WBL condition of Δ f /f _m , f (t )/f _m <10⁻⁵ as before.

Each time we measured the leaving times of cells dispersed in a suspension, we looked for an appropriate spot at which a few cells having a similar size could simultaneously experience the FM-DEP above the substrate, and the microelectrode tips were placed at the measurable position using the micromanipulator. We continued such scanning inside the cell suspensions until the FM-DEP trajectories of 10 cells were collected in total at a couple of appropriate positions. For each kind of cell, the measurement of 10 cells was repeated twice using different drops of the same cell suspension. As mentioned, it is indispensable for the implementation of the FM-DEP measurement at each spot to suppress the electrically induced solvent flows as much as possible. Hence, we traced only two cycles of the U-turn path so that the duration time of applying the electric field could be adjusted to be less than 10 s, and, correspondingly, the leaving time of each cell is given as the average of each trajectory, including the two U-turns. The mean leaving time $\overline {\Delta t_{n}}$ of each cell suspension is thus obtained from averaging the leaving times of 20 cells. Particularly for human RB cells, we further averaged three sets of the mean crossover frequencies obtained for three RB cell suspensions of three human beings, supposing that cells of the same species are similar in C _m and σ _cyt as well as in R . The two-step averaging of Δ t _n will be denoted by $\left <\overline {\Delta t_{n}}\right>$. Substituting into Eq. (10) the experimental data of either $\overline {\Delta t_{n}}$ or $\left <\overline {\Delta t_{n}}\right>$, the mean crossover frequency <f _X> was obtained.

Figure 6 shows the σ _out -dependencies of <f _X> measured for the above three kinds of biological cells using the FM-DEP method. The solid lines in Fig. 6 depict the best-fit results of Eq. (15). We evaluated C _m and σ _cyt from the best fitting of Eq. (15) into which the observed radii (R _obs ) were inserted. Table 1 lists the fitting results of C _m and σ _cyt , where we used the observed radii of 10 μ m ≤ 2R _obs ≤ 15 μ m for TL and BL cells, and 7.5 μ m ≤ 2R _obs ≤ 10 μ m for RB cells in evaluating C _m . It is to be noted from Table 1 that different species have different membrane capacitances, which are in good agreement with those reported in the literature [40–47]; the C _m values of RB cells with stationary whole blood samples from normal (healthy) donors are in excellent agreement with our value [46, 47], but are substantially higher than those of washed RB cells in isotonic buffered saline as noted in [47]. The best-fit results simultaneously provided cytoplasmic conductivities, which were consistently similar as seen from Table 1, but were slightly lower than the range of previous reports that 0.2 S/m ≤σ _cyt ≤1 S/m [40, 45, 48–51]. These results support that the FM-DEP method retains the practical reliability needed for the treatment of living cells.

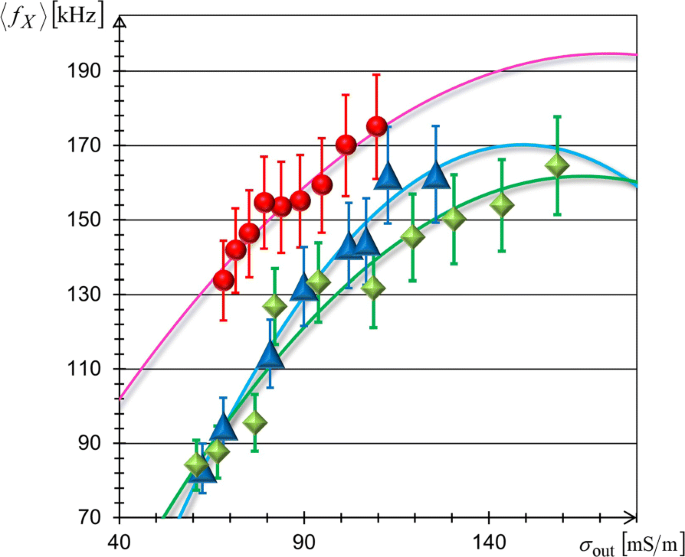
Conductivity dependences of crossover frequencies. Mean crossover frequency, <f _X>, of TL cells (blue triangles), BL cells (green diamonds), and RB cells (red circles) varying with increase of solution conductivity σ _out . The best-fit results of Eq. (15) are delineated by the solid lines

Conclusiones

Our theoretical treatment of the FM-DEP has mainly focused on the WBL condition. In this limit, we have proved theoretically that the direction of the FM-DEP force switches each time when the instantaneous frequency of the FM wave traverses the crossover frequency, thereby implying the periodic U-turns of micro/nanoparticles that undergo the FM-DEP. Two kinds of experiment have demonstrated the accuracy and reliability of f _X obtained from the observed trajectories of MLVs and cells using our formulation of the FM-DEP (Eqs. (9) and (11)):While the f _X evaluated from the FM-DEP of a single MLV coincides with that obtained from the force measurement of the same MLV experiencing AC-DEP, the conductivity dependencies of f _X provide the membrane capacitances of various cells that are in close agreement with the literature values. In other words, it has been validated theoretically and experimentally that the FM-DEP in the WBL limit can be mimicked by the time-varying AC-DEP induced by the AC wave with its frequency changing continuously according to the periodic function of f (t ). The simple view applies to other electrokinetics, including the twDEP and the electrorotation by applying the FM wave that has the spatial dependence of the phase as well as the magnitude. The AC- and FM-DEPs are associated with the real part of the dielectric spectra (or the CM factor), whereas the electrokinetics due to the spatial gradient of the phase reflect the imaginary part of the CM factor as mentioned before. Therefore, the application of the FM wave to either twDEP or electrorotation will be required for completing the dielectric characterization (the dielectric spectroscopy, in general) using the electrokinetics.

We have treated microparticles such as MLVs and cells for the precise tracking of particle trajectories. In these experiments, sedimented particles as well as floating ones have been observed; we need to increase the magnitude of electric field for inducing the DEP of the sedimented particles which are likely to be aggregated. Accordingly, we have used the plug-in system for applying the FM wave to a targeted particle floating above the substrate.

It is promising to further develop the FM-DEP method for smaller particles with their sizes of submicron to nanoscale, such as dispersed carbon nanotubes, thereby opening up the possibility of real-time spectroscopy using the FM-DEP as described below. When we apply the FM wave to the smaller colloids using the on-chip systems whose electrode configuration is designed to create a constant gradient of the applied electric field, the time-varying velocity vector v (t ) of the FM-DEP caused by the time dependence of the FM-DEP force is ascribed to the variation in χ (f ) (or the real part of the CM factor):it is found from Eqs. (9) and (12) that

$$ \boldsymbol{v}(t)=\frac{\nabla\boldsymbol{A}^{2}_{\text{RMS}}}{6\pi\eta R}\chi\{f(t)\}. $$ (16)

Hence, measuring the velocity vector v (t ) of a submicron to nanoparticle could provide the frequency dependence of the real part of the CM factor directly, which would be nothing but the electrokinetic FM spectroscopy.

Abreviaturas

AC:: Alternating current
BL:: B cell leukemia
CM:: Clausius-Mossotti
DEP:: Dielectrophoresis
DOPC:: 1,2-Dioleoyl-sn-glycero-3-phosphatidylcholine
FM:: Frequency modulated
MLV:: Multilamellar vesicle
RB:: Red blood
RMS:: Root mean squared
TL:: T cell leukemia
twDEP:: Traveling wave dielectrophoresis
WBL:: Wide band limit

Fotodetector controlado por longitud de onda basado en Nanobelt de CdSSe único Mejora significativa de fotodetectores de metal-semiconductor-metal de MgZnO mediante el acoplamiento con plasma de superficie de nanopartículas de Pt

Nanomateriales

Materiales poliméricos

Biologicos

Teñir

Especias