Estructura electrónica dependiente de espín y valle en silicene bajo potenciales periódicos

Antecedentes

Los materiales Dirac bidimensionales (2D) con estructuras de celosía hexagonal se están explorando ampliamente desde el descubrimiento del grafeno, como el siliceno [1, 2], los dicalcogenuros de metales de transición [3, 4] y el fosforeno [5]. Aunque el grafeno tiene muchas propiedades particulares, su aplicación está limitada por la banda prohibida cero y la débil interacción espín-órbita (SOI). Recientemente, se ha fabricado un análogo de silicio del grafeno, el silicene, a través del crecimiento epitaxial [6-10], y su estabilidad ha sido predicha por estudios teóricos [11, 12]. El grafeno y el siliceno tienen estructuras de bandas similares alrededor de K y K ^′ valles, y los espectros de baja energía de ambos se describen mediante la ecuación relativista de Dirac [13]. A diferencia del grafeno, el silicene tiene un SOI intrínseco fuerte y una estructura pandeada. El SOI fuerte podría abrir una brecha en los puntos de Dirac [13, 14] y conducir a un acoplamiento entre los grados de libertad de giro y valle. La estructura pandeada nos permite controlar la banda prohibida mediante un campo eléctrico externo perpendicular a la lámina de silicio [14-16]. Además, el siliceno tiene la ventaja de que es más compatible con la tecnología electrónica existente basada en silicio. Estas características hacen del siliceno un material excelente para la nanoelectrónica de próxima generación. En particular, un transistor de efecto de campo de silicio a temperatura ambiente se ha fabricado con éxito mediante un proceso de fabricación de transferencia de crecimiento en el experimento [17].

El descubrimiento de materiales 2D de Dirac ofrece nuevas oportunidades para explorar el control cuántico del valle. Los dos valles desiguales K y K ^′ en la primera zona de Brillouin podría considerarse como un grado adicional de libertad además de la carga y el espín para la información cuántica y el cálculo cuántico [18-20]. Por ejemplo, el grado de libertad de valle se puede incorporar para expandir un qubit de espín electrónico a un qubit de valle de espín [18]. Por lo tanto, Valleytronics, que tiene como objetivo generar, detectar y manipular la pseudoespina del valle, ha atraído un interés considerable. En el grafeno, se han propuesto varios esquemas para lograr una polarización de valle utilizando modos de borde únicos [21, 22], efecto de deformación trigonal [23], defectos de la línea topológica [24, 25], deformación [26, 27] y puertas electrostáticas. [28]. En comparación con el grafeno, el silicene tiene una ventaja significativa en el estudio de la pseudoespina del valle. Se encuentra que el siliceno exhibe una rica variedad de fases topológicas y números de Chern bajo la modulación de diferentes campos externos [13, 16, 29, 30]. En presencia de campo eléctrico E _z y campo de intercambio h , Ezawa exploró el diagrama de fase en el E _z - h plano que se caracteriza por los índices de espín y valle [16]. Considerando además el Rashba SOI, un estado de Hall anómalo cuántico polarizado en valle se predice en silicene debido a la transición de fase topológica [31]. Sobre la base de la transición de estado, se propone un filtro de espín basado en silicio con casi el 100% de polarización de espín, que es robusto contra el desorden débil [32]. Yokoyama estudió el transporte balístico a través de una unión de siliceno ferromagnético (FM) y demostró un espín controlable y una corriente polarizada en valle [33]. En dicalcogenuros de metales de transición con una simetría de inversión rota, la división de espín de las bandas de valencia que surgen del SOI intrínseco es opuesta en los dos valles debido a una simetría de inversión en el tiempo [3, 34, 35]. La simetría de inversión rota podría resultar en una regla de selección óptica dependiente del valle, que puede usarse para excitar selectivamente portadoras en el K o K ^′ valle a través de luz polarizada circularmente hacia la derecha o hacia la izquierda, respectivamente [3, 34]. En el experimento, la señal de polarización de valle ha sido probada mediante mediciones ópticas [36, 37] y de transporte [38, 39]. Se observó un efecto Hall gigante de valle no local en el grafeno bicapa sometido a un campo eléctrico de puerta que rompe la simetría, y la señal no local persiste hasta la temperatura ambiente [38]. En la ref. [40].

Superlattice es un método eficaz de ingeniería de la estructura electrónica en semiconductores y materiales 2D [41]. Los patrones de superrejilla con nanoescala pueden surgir naturalmente en los experimentos cuando se coloca grafeno o siliceno sobre sustratos metálicos [42, 43]. Una superrejilla en el grafeno podría conducir a la renormalización de la velocidad de Fermi anisotrópica [44] y la generación de nuevos puntos de Dirac en el espectro [45-47] debido a la naturaleza quiral, que se han observado experimentalmente [43, 48, 49]. En superredes de silicio con campo eléctrico E _z y campo de intercambio h , se eliminan las degeneraciones tanto de espín como de valle. Se confirma que la estructura de minibanda y los minigaps causados ​​por las superredes dependen de los índices de espín y valle [50]. Además, las polarizaciones de espín y valle podrían mejorarse mediante las superredes de silicio [51]. Al igual que el grafeno, se esperan muchas estructuras electrónicas novedosas en superredes de silicio. Sin embargo, los trabajos sobre superredes de silicio son muy pocos [50, 51]. En este artículo, discutimos en detalle un aspecto complementario, a saber, la estructura de bandas dependiente de espín y valle y la propiedad de transporte del silicene. Descubrimos que los índices de espín y valle tienen diferentes impactos en los puntos de Dirac adicionales y la velocidad anisotrópica que pueden ajustarse mediante los parámetros estructurales. La velocidad se suprime en gran medida debido al campo eléctrico y al campo de intercambio. Se logra una notable polarización de espín y valle, que el desorden puede mejorar en gran medida.

El documento está organizado de la siguiente manera. En el apartado de “Métodos” presentamos el formalismo teórico y la relación de dispersión. Los resultados numéricos sobre la estructura de bandas, las transmisiones polarizadas de espín y valle se muestran en la sección "Resultados y discusiones". Finalmente, concluimos con un resumen en la sección "Conclusiones".

Métodos

En la aproximación de una sola partícula, la estructura electrónica del silicene en la vecindad de los puntos de Dirac obedece a un Dirac hamiltoniano efectivo. El sistema en consideración es una superrejilla de silicio unidimensional formada por una serie de barreras potenciales locales U , campos de intercambio h y campo eléctrico perpendicular E _z . U , h y E _z están presentes solo en las regiones de barrera con ancho de barrera d _b , mientras que U = h = E _z =0 en las regiones de pozos con ancho de pozo d _w , como se muestra en la Fig. 1. La superrejilla con un tipo de Kronig-Penney varía solo a lo largo de x dirección, y la longitud de una unidad es d = d _b + d _w . Se ha discutido un modelo similar en las Refs. [51, 52], que se centran principalmente en el transporte termoeléctrico y electrónico más que en la estructura de bandas y el efecto de desorden estudiados en este trabajo. Experimentalmente, U puede ser producido por las puertas metálicas y h puede producirse por el efecto de proximidad magnética con aislantes FM EuO [33], que se depositan periódicamente sobre la capa de silicio (ver Fig. 1). El campo eléctrico E _z aplicado perpendicular al silicene puede inducir un potencial de subred escalonado Δ _z = ℓ E _z , con 2 ℓ ≈0.46Å la separación vertical de A y B sitios de las dos subredes debido a la estructura pandeada [16]. Por tanto, los estados electrónicos pueden ser descritos por el hamiltoniano,

$$ \ begin {array} {@ {} rcl @ {}} H =\ hbar v_ {F} (k_ {x} \ tau_ {x} - \ eta k_ {y} \ tau_ {y}) + \ Delta_ {\ eta \ sigma} \ tau_ {z} + U _ {\ sigma}. \ end {array} $$ (1)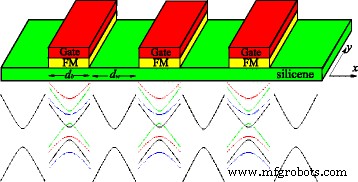

Arriba:esquema de las superredes de silicio. Los aislantes de FM, como EuO y EuS, en la parte superior del silicene inducen los campos de intercambio en silicene, como se propone para el grafeno [53]. Las puertas metálicas en la parte superior de los aisladores FM controlan el nivel Fermi localmente. Abajo:esquema del espectro energético en silicio con y sin campos externos

Δ _{η σ} = Δ _z - η σ λ _SO describe la banda prohibida para diferentes índices de espín y valle, que pueden ser controlados por el potencial escalonado Δ _z y el SOI λ _SO . U _σ = U - σ h es el potencial efectivo para diferentes índices de giro. η =± 1 denota la K y K ^′ valles. σ =± 1 denota estados de aceleración y desaceleración. v _F es la velocidad de Fermi. En silicene, los efectos intrínsecos y extrínsecos de Rashba son muy pequeños y pueden pasarse por alto [15].

Debido a la invariancia traslacional a lo largo de y dirección, el vector de onda transversal k _y se conserva. La función de onda para valle η y gire σ en cada región tiene la forma Ψ ( x , años ) = ψ ( x ) e ^iky _y con

$$ \ begin {array} {@ {} rcl @ {}} \ psi (x) =A \ left (\ begin {array} {cc} 1 \\ \ frac {\ hbar v_ {F} k _ {-} } {\ epsilon _ {\ eta \ sigma}} \ end {matriz} \ right) e ^ {i q _ {\ eta \ sigma} x} + B \ left (\ begin {matriz} {cc} 1 \\ \ frac {- \ hbar v_ {F} k _ {+}} {\ epsilon _ {\ eta \ sigma}} \ end {matriz} \ right) e ^ {- i q _ {\ eta \ sigma} x}. \ end {matriz} $$ (2)

En las regiones de barrera, ε _{η σ} = ε _b =( E - U _σ ) + Δ _{η σ} y el x componente del vector de onda \ (q _ {\ eta \ sigma} =q_ {b} =\ sqrt {(E - U _ {\ sigma}) ^ {2} - \ Delta ^ {2} _ {\ eta \ sigma} - (\ hbar v_ {F} k_ {y}) ^ {2}} / \ hbar v_ {F} \). En las regiones de pozos, ε _{η σ} = ε _w = E - η σ λ _SO y \ (q _ {\ eta \ sigma} =q_ {w} =\ sqrt {E ^ {2} - \ lambda _ {SO} ^ {2} - (\ hbar v_ {F} k_ {y}) ^ { 2}} / \ hbar v_ {F} \). k _± = q _{η σ} ± yo η k _y . La probabilidad de transmisión T _{η σ} se puede calcular utilizando la técnica de matriz de transferencia. La conductancia normalizada para un giro particular en un valle particular a temperatura cero viene dada por

$$ \ begin {array} {@ {} rcl @ {}} G _ {\ eta \ sigma} (E) =\ frac {1} {2} \ int _ {- \ pi / 2} ^ {\ pi / 2 } T _ {\ eta \ sigma} (E, E \ sin \ theta) \ cos \ theta d \ theta, \ end {matriz} $$ (3)

donde θ es el ángulo de incidencia con respecto a la x dirección. Las conductancias resueltas por espín y valle se definen como \ (G _ {\ uparrow (\ downarrow)} =\ left (G_ {K \ uparrow (\ downarrow)} + G_ {K ^ {\ prime} \ uparrow (\ downarrow )} \ right) / 2 \) y \ (G_ {K (K ^ {\ prime})} =\ left (G_ {K (K ^ {\ prime}) \ uparrow} + G_ {K (K ^ { \ prime}) \ downarrow} \ right) / 2 \), respectivamente. Luego, introducimos la polarización de espín P _s y polarización de valle P _v :

$$ \ begin {array} {@ {} rcl @ {}} P_ {s} =(G _ {\ uparrow} - G _ {\ downarrow}) / (G _ {\ uparrow} + G _ {\ downarrow}), \ end {array} $$ (4) $$ \ begin {array} {@ {} rcl @ {}} P_ {v} =(G_ {K} - G_ {K ^ {\ prime}}) / (G_ { K} + G_ {K ^ {\ prime}}). \ end {matriz} $$ (5)

Basado en el teorema de Bloch y la condición de continuidad de las funciones de onda, la relación de dispersión E ( k _x ) para electrones de spin-up y spin-down cerca de K y K ^′ los valles se pueden calcular,

$$ \ begin {alineado} \ cos (k_ {x} d) &=\ cos (q_ {w} d_ {w}) \ cos (q_ {b} d_ {b}) \\ &\ quad- \ frac {(\ epsilon_ {b} q_ {w}) ^ {2} + (\ epsilon_ {w} q_ {b}) ^ {2} + (\ epsilon_ {b} \! - \! \ epsilon_ {w}) ^ {2} k ^ {2} _ {y}} {2 \ epsilon_ {w} \ epsilon_ {b} q_ {w} q_ {b}} \ sin (q_ {w} d_ {w}) \ sin ( q_ {b} d_ {b}), \ end {alineado} $$ (6)

y k _x es el número de onda de Bloch. Para simplificar el cálculo, se introducen las unidades adimensionales:\ (E \ rightarrow E d / \ hbar v_ {F} \), \ (U \ rightarrow U d / \ hbar v_ {F} \), \ (\ lambda _ {SO} \ rightarrow \ lambda _ {SO} d / \ hbar v_ {F} \), \ (\ Delta _ {z} \ rightarrow \ Delta _ {z} d / \ hbar v_ {F} \) , \ (h \ rightarrow hd / \ hbar v_ {F} \), k _y → k _y d , k _x → k _x d , d _w → d _w / d y d _b → d _b / d . Tenga en cuenta que en Δ _z = λ _SO = h =0, ecuación. (6) se reduce al encontrado para el grafeno sin espacios en un potencial periódico, donde tanto el espín como el valle están degenerados [44-47]. De la ecuación. (6), podemos ver ese campo de intercambio h solo podría inducir la escisión del giro, mientras que el valle mantiene la degeneración. Sin embargo, la degeneración del valle puede ser eliminada por el campo eléctrico E _z con la ayuda de SOI λ _SO . Por lo tanto, una combinación del campo de intercambio y el campo eléctrico podría levantar las degeneraciones de espín y valle [16, 31-33], como se muestra en la Fig. 1. En el sistema propuesto, los electrones con espines diferentes cerca de valles diferentes presentarían varias bandas estructuras y características de transporte.

Resultados y discusiones

En esta sección, usaríamos las ecuaciones anteriores para calcular las estructuras de bandas y las propiedades de transporte para diferentes índices de espín y valle en superredes de silicio. Se supone que los anchos de las barreras y los pozos son los mismos en lo que sigue. Los resultados para el caso con anchos desiguales de pozo y barrera ( d _b ≠ d _w ) son similares a los del grafeno sin espacios [47]. Algunos parámetros se establecen como d _b = d _w =50 nm y λ _SO =3,9 meV en siliceno, a menos que se indique lo contrario. Nos concentraremos en las dos primeras minibandas (las minibanda de valencia y conducción más bajas) cerca del nivel de Fermi.

Estructura de banda dependiente de valle y giro

Primero, el efecto del potencial U en minibanda se muestra en la Fig. 2. Para discutir el caso con huecos y el caso sin huecos de las bandas de energía simultáneamente, establecemos Δ _z =7,8 meV =2 λ _SO . En ausencia de potencial ( U =0), el electrón de spin-up cerca de K valle ( K ↑ electrón) y electrón de spin-down cerca de K ^′ valle ( K ^′ ↓ electrón) no tienen espacios (ver Fig.2 (a1, a4)), mientras que el electrón de spin-down cerca de K valle ( K ↓ electrón) y electrón de spin-up cerca de K ^′ valle ( K ^′ ↑ electrón) tienen un gran espacio (ver Fig.2 (a2, a3)). Las minibanda del electrón de giro hacia arriba (o hacia abajo) se desplazan al rango de energía negativa (o positiva) de E =0 por h , debido al potencial efectivo U _σ = U - σ h . Las estructuras de bandas de K ↑ (o K ↓ ) electrón y K ^′ ↓ (o K ^′ ↑ ) simetría especular presente de electrones con respecto a E =0, consistente con la Ec. (6). Sin embargo, esta simetría de espejo se destruye en presencia de U . Obviamente, como U aumenta, aparecen puntos Dirac adicionales, cuyo número aumenta mientras tanto. Los puntos de Dirac adicionales se pueden demostrar por la quiralidad de las funciones de onda en su vecindad [46]. Las características de los puntos de Dirac en el sistema silicene dependen en gran medida de los grados de libertad de giro y valle, como se muestra en la Fig. 2. Por ejemplo, en U =135 meV en la Fig. 2 (d1 – d4) para K ↑ , K ↓ , K ^′ ↑ y K ^′ ↓ electrones, el número de puntos de Dirac es 5, 6, 4 y 7, respectivamente. Para valores específicos de U , como U =40,66 meV para K ↓ electrón (ver Fig.2 (b2)) y U =100,63 meV para K ^′ ↑ electrón (ver Fig.2 (c3)), se puede generar un nuevo punto de Dirac en k _y =0, y se dividirá en un par que se moverá en direcciones opuestas alejándose del k _y =0 punto pero siempre manteniendo k _x =0, como U aumentos adicionales. En consecuencia, los huecos de banda para K ↓ y K ^′ ↑ los electrones están cerrados (vea la Fig. 2 (b2, c3)), y el sistema con huecos se vuelve sin huecos. Para encontrar el valor crítico de U , configuramos d _b = d _w y k _x =0. De manera análoga a la regla del grafeno sin espacios [47], teniendo en cuenta el teorema de la función implícita, se puede concluir que los vectores de onda longitudinales en los nuevos puntos de Dirac satisfacen q _b = q _w cuando

$$ \ begin {array} {@ {} rcl @ {}} E_ {0} =\ frac {(U - \ sigma h) ^ {2} - \ Delta_ {z} ^ {2} + 2 \ eta \ sigma \ Delta_ {z} \ lambda_ {SO}} {2 (U - \ sigma h)}. \ end {array} $$ (7)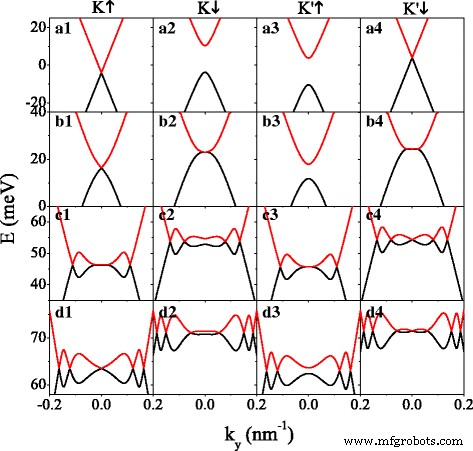

Espectro energético frente a k _y para varios valores diferentes de potencial U . (a1 – a4) U =0; (b1 – b4) U =40,66 meV; (c1 – c4) U =100,63 meV; (d1 – d4) U =135,0 meV. Los valores de los parámetros son h =8,0 meV, Δ _z =7,8 meV y k _x =0

Para K ↑ y K ^′ ↓ electrones con η σ =1, cuando Δ _z =2 λ _SO , Eq. (7) se puede reducir a

$$ \ begin {array} {@ {} rcl @ {}} E_ {0} =\ frac {U - \ sigma h} {2}. \ end {matriz} $$ (8)

En consecuencia, Eq. (6) se convierte en

$$ {} \ cos ^ {2} (q_ {w} d_ {w}) - \ frac {\ left (\ epsilon_ {b} ^ {2} + \ epsilon_ {w} ^ {2} \ right) q_ {w} ^ {2} + (\ epsilon_ {b} - \ epsilon_ {w}) ^ {2} k ^ {2} _ {y}} {2 \ epsilon_ {w} \ epsilon_ {b} q_ {w } ^ {2}} \ sin ^ {2} (q_ {w} d_ {w}) =1, $$ (9)

que se satisface cuando \ (\ left (\ epsilon _ {b} ^ {2} + \ epsilon _ {w} ^ {2} \ right) q_ {w} ^ {2} + (\ epsilon _ {b} - \ epsilon _ {w}) ^ {2} k ^ {2} _ {y} =-2 \ epsilon _ {w} \ epsilon _ {b} q_ {w} ^ {2} \) o q _w d =2 n π ( n es un número entero positivo). Basado en Eq. (8), tenemos ε _b =- ε _w , por lo que la igualdad anterior se cumple solo si k _{y 0} =0 para K ↑ y K ^′ ↓ electrones en Δ _z =2 λ _SO , correspondiente al punto de Dirac original. Las soluciones de q _w d =2 n π tener la forma

$$ \ begin {array} {@ {} rcl @ {}} k_ {y0} =\ pm \ frac {1} {d} \ sqrt {\ frac {\ left (E_ {0} ^ {2} - \ lambda_ {SO} ^ {2} \ right) d ^ {2}} {(\ hbar v_ {F}) ^ {2}} - (2n \ pi) ^ {2}}. \ end {matriz} $$ (10)

Cuando \ (\ sqrt {E_ {0} ^ {2} - \ lambda _ {SO} ^ {2}} d / 2 \ pi \ hbar v_ {F} \ geq n \), k _{y 0} es real, y surgirán los nuevos puntos de Dirac que están ubicados exactamente en ( E ₀ , k _{y 0} ). A valores bajos de U , k _{y 0} es imaginario y no hay solución para n , lo que significa que no hay puntos Dirac adicionales. Los puntos de Dirac aparecen solo después de un valor crítico de U , como U =40,66 meV para K ↓ electrones en la Fig.2 (b2), correspondientes a n =1. Según Eq. (10), el número de puntos Dirac N _D Puede ser obtenido. Cuando Δ _z =2 λ _SO ,

$$ \ begin {array} {@ {} rcl @ {}} N_ {D} =2 \ left [\ frac {\ sqrt {E_ {0} ^ {2} - \ lambda_ {SO} ^ {2}} d} {2 \ pi \ hbar v_ {F}} \ right] + 1 \ end {array} $$ (11)

para K ↑ y K ^′ ↓ electrones, mientras

$$ \ begin {array} {@ {} rcl @ {}} N_ {D} =2 \ left [\ frac {\ sqrt {E_ {0} ^ {2} - \ lambda_ {SO} ^ {2}} d} {2 \ pi \ hbar v_ {F}} \ right] \ end {array} $$ (12)

para K ↓ y K ^′ ↑ electrones, donde [...] denota una parte entera. Tenga en cuenta que en el valor crítico de U , como U =40,66 meV y 100,63 meV, el número de puntos de Dirac es N _D =2 n −1 para K ↓ y K ^′ ↑ electrones (ver Fig. 2 (b2, c3)).

Las ecuaciones (7) y (10) manifiestan que las posiciones y el número de puntos de Dirac pueden ser ajustados por el campo eléctrico E _z y campo de intercambio h . La Figura 3 muestra el número de puntos de Dirac N _D en función de U para diferentes valores de E _z y h . Cuando Δ _z =7,8 meV en la Fig. 3a, con U en aumento , N _D para K ↑ y K ^′ ↓ los electrones aumentan en forma de número impar, de acuerdo con la ecuación. (11). N _D para K ↓ y K ^′ ↑ los electrones aumentan en forma de número par, de acuerdo con la ecuación. (12), excepto N _D en el valor crítico. La comparación entre la Fig. 3a yb indica que como h aumenta, el valor crítico para el electrón de spin-down (o spin-up) disminuye (o aumenta) gradualmente. Cuando Δ _z =15 meV ≠ 2 λ _SO en la Fig. 3c, N _D para todos los electrones aumenta en forma de número par, excepto para N _D en el valor crítico. Claramente, los valores críticos de U son diferentes para los electrones con diferentes espines y valles. Los puntos de Dirac podrían controlarse mediante una modulación conjunta de los parámetros U , E _z y h .

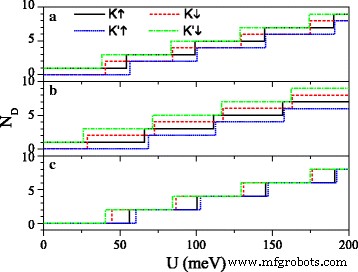
Número de puntos Dirac N _D versus potencial U . ( a ) h =8.0 meV y Δ _z =7,8 meV; ( b ) h =20,0 meV y Δ _z =7,8 meV; ( c ) h =8.0 meV y Δ _z =15,0 meV

El potencial U y ancho de barrera d _b podría usarse para regular la banda prohibida, como se ilustra en la Fig. 4. Las brechas para K ↑ y K ^′ ↓ los electrones son pequeños, mientras que los espacios para K ↓ y K ^′ ↑ los electrones son grandes debido a Δ _{η σ} = Δ _z - η σ λ _SO . Como U aumenta, todas las minibanda se mueven gradualmente hacia la región de alta energía (ver Fig. 4a), y todos los espacios de banda muestran una oscilación amortiguada con U (ver Fig. 4b). Cuando U = σ h , el potencial efectivo es cero y la brecha alcanza el valor máximo. La brecha se cierra en el valor crítico de U , a causa de la aparición de nuevos puntos de Dirac. La Figura 4c, d muestra la dependencia de las minibanda y los espacios de banda en el ancho de la barrera d _b en U =0. En ausencia de campo externo ( d _b =0), las minibandas se mantienen degeneradas y la brecha en el nivel de Fermi es 2 λ _SO . Con la aparición de d _b , la minibanda se divide, donde el valle y el giro se vuelven no degenerados. Las minibanda de K ↑ (o K ↓ ) y K ^′ ↓ (o K ^′ ↑ ) los electrones mantienen una simetría especular alrededor de E =0 (ver Fig. 4c). Como d _b aumenta, las brechas de K ↓ y K ^′ ↑ los electrones se amplían gradualmente. Las lagunas de K ↑ y K ^′ ↓ los electrones disminuyen a cero cuando d _b satisface d _b / d _w = λ _SO / Δ _z , y luego aumentar con d _b (ver Fig. 4d). Los anchos de brecha se acercan a la saturación con el aumento adicional de d _b . Además, el ancho de la minibanda se reduce como d _b aumenta (no se muestra en la figura), debido al menor acoplamiento de autoestados. El efecto del campo eléctrico sobre la banda prohibida es análogo al del estudio anterior [50].

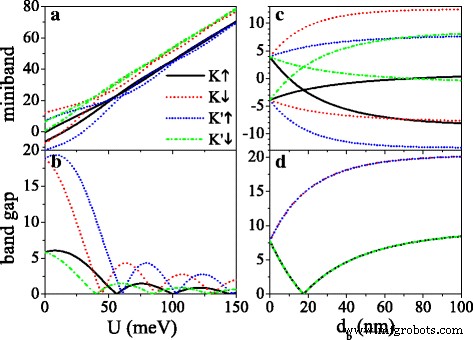
( a ) Minibanda cerca del nivel Fermi y ( b ) sus huecos de banda en el punto Dirac original frente a la U potencial , en d _b = d _w =50 nm. ( c ) Minibanda cerca del nivel Fermi y ( d ) sus intervalos de banda en el punto Dirac original frente a d _b , en U =0 y d _w =50 nm. Los valores de otros parámetros son h =8,0 meV, Δ _z =15,0 meV y k _x = k _y =0

La velocidad del grupo depende en gran medida de los índices de espín y valle, como se muestra en la Fig. 5. Los componentes ( v _x , v _y ) de velocidad se puede definir como

$$ \ begin {matriz} {@ {} rcl @ {}} v_ {x} / v_ {F} =\ E parcial / \ parcial k_ {x}, \ quad v_ {y} / v_ {F} =\ parcial E / \ parcial k_ {y}. \ end {array} $$ (13)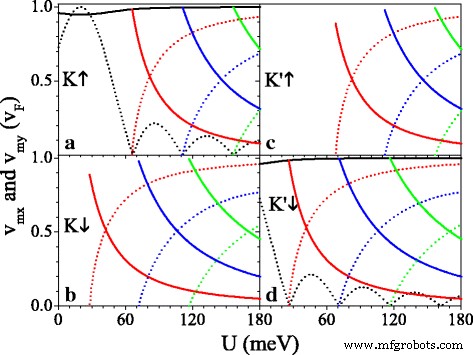

( a - d ) Velocidad versus potencial U , y los parámetros se establecen como h =20,0 meV y Δ _z =7,8 meV. Las curvas sólidas negras, rojas, azules y verdes son las velocidades v _{0 x} , v _{1 x} , v _{2 x} y v _{3 x} , respectivamente. Las curvas de trazos negros, rojos, azules y verdes son las velocidades v _{0 años} , v _{1 año} , v _{2 años} y v _{3 años} , respectivamente

La Figura 5 presenta los componentes de la velocidad v _mx y v _mi en unidades de v _F en el punto original de Dirac ( m =0) y nuevos puntos de Dirac ( m =1,2,3). Uno puede ver eso como U aumenta, v _{0 años} oscila de forma decadente y v _{0 x} ≈ v _F casi no se ve afectado (ver Fig. 5a, d). En el valor crítico de U donde emergen los nuevos puntos de Dirac, v _mx ≈ v _F pero v _{0 años} = v _mi =0, lo que indica un comportamiento de colimación a lo largo de la k _x dirección para giros y valles específicos. Cuando U supera el valor crítico y aumenta aún más, v _mi aumentar a v _F pero v _mx disminuya a cero gradualmente. El efecto del potencial periódico es altamente anisotrópico, como resultado de la naturaleza quiral. Las características de la velocidad anisotrópica son diversas para diferentes espines y valles debido a la brecha Δ _{η σ} y el potencial U _σ , que se puede ordenar empleando U . Tomando U =20 meV por ejemplo, v _{0 años} = v _F para K ↑ el electrón es mucho mayor que v _{0 años} =0,16 v _F para K ^′ ↓ electrón, y no v _{0 años} para K ↓ y K ^′ ↑ electrones debido a la banda prohibida. v _mx (o v _mi ) para el electrón de spin-up es siempre mayor (o menor) que el del electrón de spin-down en el mismo valle. En particular, la Fig.5 también implica que para un valor pequeño de U , v _{0 x} , v _{0 años} y v _mx son menores que v _F debido a Δ _z y h , salvo el sistema gapless [44]. Por ejemplo, v _{1 x} =0,98 v _F , 0,89 v _F , 0,89 v _F y 0,98 v _F para K ↑ , K ↓ , K ^′ ↑ y K ^′ ↓ electrones, respectivamente, cuando aparece el punto de Dirac. Para iluminar la influencia de Δ _z y h en la velocidad del grupo, la Fig.6 muestra las velocidades ( v _{0 x} , v _{0 años} ) en función de (a) Δ _z y (b) h para K ↑ electrón. De la Fig. 6a podemos ver claramente que v _{0 x} está disminuyendo monótonamente con Δ _z mientras que v _{0 años} es insensible al cambio de Δ _z . Por el contrario, v _{0 x} está insensible a h , mientras que v _{0 años} aumenta al valor máximo v _{0 años} = v _F a las h = σ U y luego disminuye con h . Los resultados indican que la velocidad del grupo puede ser suprimida por Δ _z y h en silicene.

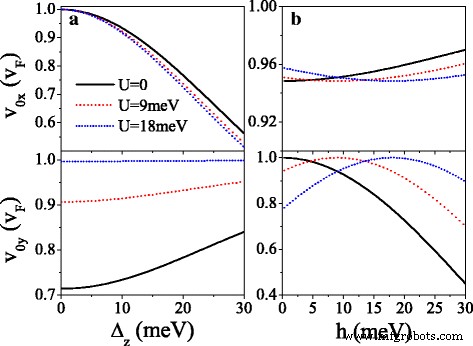
Velocidades v _{0 x} y v _{0 años} versus ( a ) Δ _z y ( b ) h , para K ↑ electrón. ( a ) h =20,0 meV y λ _SO = Δ _z / 2. ( b ) Δ _z =7,8 meV

Transporte polarizado con giro y valle

La estructura de bandas dependiente de espín y valle se refleja en la propiedad de transporte y proporciona una guía para controlar el transporte. En esta sección, discutimos las propiedades del transporte polarizado de espín y valle a través de una superrejilla de silicio finita. La Figura 7 muestra la probabilidad de transmisión T _{η σ} para (a, c) K ↑ y (b, d) K ↓ electrones, y el número de período n =10. Las curvas de trazos rojos son las minibanda, que también son las fronteras de los diferentes estados electrónicos que deciden la transmisión. Podemos ver que la transmisión está restringida en la región de minibanda y no hay transmisión en la región de banda prohibida (ver Fig. 7a, b). La distribución de la transmisión es simétrica alrededor de k _y =0 debido a las minibanda simétricas. La característica resonante de transmisión surge de los estados resonantes. Cabe señalar que la transmisión todavía existe en la región de la brecha cerca de k _y =0 debido al efecto túnel de los autoestados. T _{η σ} al nivel de Fermi para K ↑ y K ↓ los electrones se muestran en la Fig. 7c, d), respectivamente. Uno puede ver claramente que muchos picos resonantes delgados con T _{η σ} =1 ocurre precisamente en las posiciones de los puntos de Dirac, lo que sugiere una aplicación del sistema como un filtro de espín y valle.

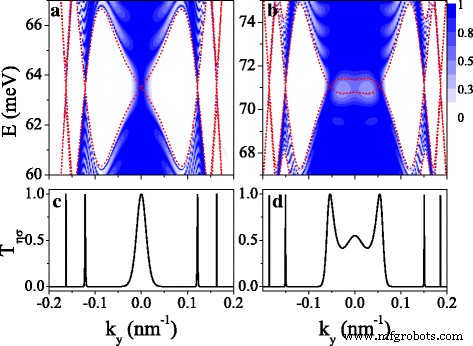
Gráfico de contorno de la transmisión T _{η σ} ( E , k _y ) para ( a ), ( c ) K ↑ electrón y ( b ), ( d ) K ↓ electrón. Los valores de los parámetros son los mismos que los de la Fig. 2 (d1 – d4) y n =10

La fuerte dependencia de la estructura de la banda de los índices de espín y valle es beneficiosa para la realización de polarizaciones de espín y valle altos. La Figura 8 presenta las minibandas, conductancias G _{η σ} , polarización de giro P _s y polarización de valle P _v en función del potencial U . Se puede encontrar que la distribución de conductancia está completamente de acuerdo con la estructura de la banda, es decir, la conductancia (o brecha de conductancia) corresponde a la minibanda (o banda prohibida). Las minibanda para los electrones de spin-up y spin-down podrían ser una distribución alternativa ajustando h adecuadamente. Consequently, \(G_{K(K^{\prime })\uparrow }\) and \(G_{K(K^{\prime })\downarrow }\) present alternative distribution as well, i.e., \(G_{K(K^{\prime })\uparrow }\) nearly vanishes for those regions where \(G_{K(K^{\prime })\downarrow }\) is in resonance and vice versa. This result directly leads to a remarkable spin polarization, proposing a switching effect of spin polarization (see Fig. 8a). By changing Δ _z , the minibands and conductances for electrons near K y K ^′ valleys could be controlled, leading to a fully valley-polarized current (see Fig. 8b). Compared with spin polarization, the valley polarization is not perfect enough. However, this drawback could be remedied via the disorder structure of the system, as discussed in the following.

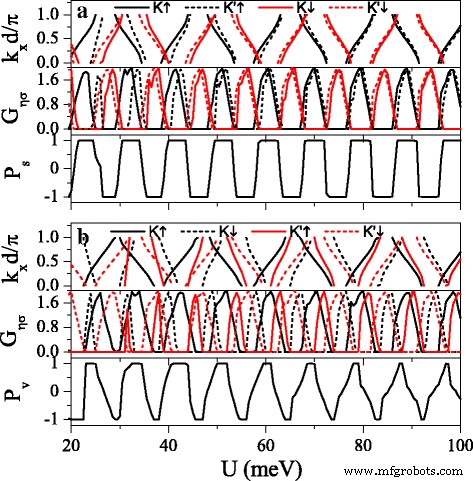
Minibands, conductances G _{η σ} , spin polarization P _s , and valley polarization P _v versus potential U . ( a ) Δ _z =4.0 meV. ( b ) Δ _z =12.0 meV. Other parameters are set as h =7.0 meV, E =6.0 meV, d _b =d _w =120 nm, and n =10

Figure 9 shows the (a) spin polarization P _s and (b) valley polarization P _v in (U ,h ) space. Interestingly, both P _s and P _v present periodical changes in the considered region, which is not observed in the ferromagnetic silicene junction [33]. Both distributions of P _s and P _v are antisymmetric with respect to h →−h . It is possible to achieve independently a full spin and valley polarization by a proper tuning of the fields U y h . For example, when h =6 meV and U =42 meV, P _s ≈1 and P _v ≈1, meaning that the current is mainly contributed by K ↑ electrones. When h =6 meV and U =44 meV, P _s ≈1 and P _v ≈−1 while P _s ≈−1 and P _v ≈−1 at h =6 meV and U =46 meV. The results demonstrate that a spin and valley polarization can be switched effectively.

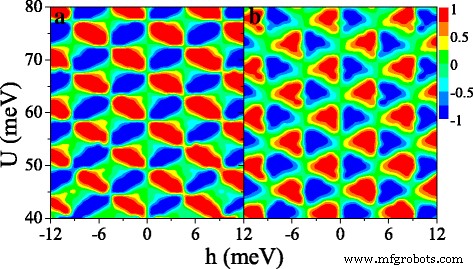
Contour plot of (a ) spin polarization P _s (U ,h ) y ( b ) valley polarization P _v (U ,h ), at Δ _z =10.0 meV. The values of other parameters are the same as these in Fig. 8

In experiment, the structural imperfection of the model is unavoidable due to the limitations of the experimental techniques. Therefore, it is necessary to discuss the effect of the disorder on transmission. When the electric field or exchange field presents disorder, the conductance, spin polarization, and valley polarization are shown in Figs. 10 and 11. We set disorder situations of Δ _z y h fluctuate around their mean values, given by 〈Δ _z 〉=Δ _{z 0} and 〈h 〉=h ₀ , respectivamente. The fluctuations are given by

$$\begin{array}{@{}rcl@{}} \Delta_{z} |_{i} =\Delta_{z0} (1 + \delta \zeta_{i}), \quad h |_{i} =h_{0} (1 + \delta \zeta_{i}), \end{array} $$ (14)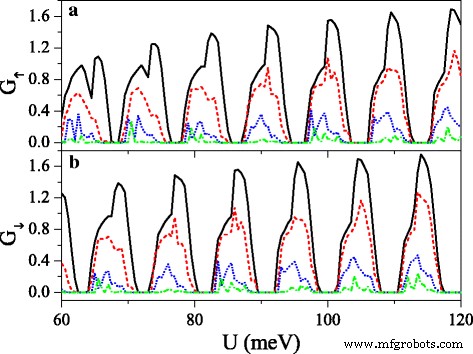

Conductances (a ) G _↑ and (b ) G _↓ versus potential U , when the electric field presents disorder, at n =50 and Δ _{z 0} =20.0 meV. The solid, dashed, dotted, and dash-dotted curves correspond to the disorder strength δ =0.0, 0.1, 0.3, and 0.6, respectively. The values of other parameters are the same as these in Fig. 8

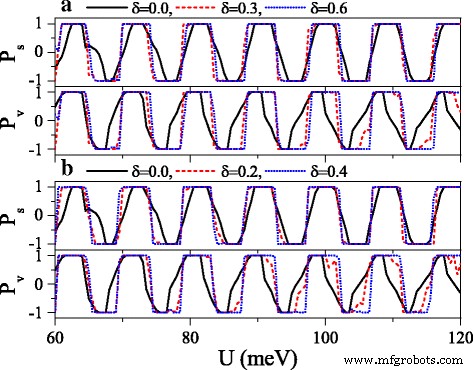
Polarizations P _s and P _v versus potential U when a the electric field or b the exchange field presents disorder. Δ _{z 0} =20.0 meV and h =7.0 meV in (a ). Δ _z =20.0 meV and h ₀ =7.0 meV in (b ). The values of other parameters are the same as these in Fig. 10

where {ζ _i } is a set of uncorrelated random variables or white noise, − 1<ζ _i <1, δ is the disorder strength, and i is the site index. Note that the disorder only takes place in the x direction, and the system is always homogeneous in y dirección. Thus, k _y still keeps conservation. Figure 10 exhibits the effect of the disorder of the electric field on the conductances (a) G _↑ and (b) G _↓ . With the presence and increase of the disorder strength δ , both G _↑ and G _↓ are suppressed gradually, and each resonant peak splits into many small peaks. One may find that the conductance range is narrowed while the conductance gap range is broadened. Hence, the allowable (or forbidden) ranges of G _↑ completely fall into the forbidden (or allowable) ranges of G _↓ , giving rise to an excellent spin polarization (see Fig. 11). Furthermore, the positions of conductances and conductance gaps are nearly invariable as δ changes, suggesting that the miniband and band gap are insensitive to the disorder. Note that the disorder effect of the electric field on G _K and G _K ^′ is similar to that observed in Fig. 10. Figure 11 presents the disorder effects of (a) the electric field and (b) the exchange field on polarizations P _s and P _v . Obviously, with the increase of δ , P _s and P _v increase greatly, and the polarization platform is broadened. Thus, a full spin and valley polarization is realized. Comparison between Fig. 11a and b indicates that the disorder effect of exchange field is more prominent. The results demonstrate that the disorder could enhance the spin and valley polarizations compared with the order case, which is an advantage in realistic application.

Conclusiones

In summary, we demonstrated detailedly that band structure and transport property of silicene under a periodic field strongly depend on the spin and valley degrees of freedom. The numerical results indicate that electrons with different spins and valleys have various characteristics in Dirac point, bang gap, and group velocity. In particular, owing to the electric field and exchange field, the anisotropic velocity is restrained, which displays a collimation behavior for specific spins and valleys. Therefore, the transmission presents strong spin- and valley-dependent feature, consistent with the band structure, resulting in a significant spin and valley polarizations. In addition, the disorder could greatly enhance the spin and valley polarizations. Finally, we hope these results can be conducive to the potential applications of the spin and valley indices.

Abreviaturas

2D:

Bidimensional

FM:

Ferromagnético

SOI:

Spin-orbit interaction

Reduzca la sensibilidad de CL-20 mejorando la conductividad térmica a través de nanomateriales de carbono Sensor de deformación ultrasensible basado en una película piezoeléctrica de poli (fluoruro de vinilideno) flexible