Efectos de la fotoconductividad, la sensibilidad al pH, el ruido y la longitud del canal en los sensores FET de nanocables de Si

Antecedentes

Durante la última década, las estructuras de silicio de tamaño nanométrico han sido objeto de un estudio intensivo [1] debido a sus prometedoras propiedades eléctricas, ópticas, químicas, térmicas y mecánicas. En comparación con las estructuras más grandes, los transistores de efecto de campo (FET) a nanoescala permiten medir señales eléctricas, ópticas y otros tipos de señales muy pequeñas debido al aumento de la relación superficie-volumen de la muestra. Los pequeños tamaños de las nanoestructuras las hacen ideales para detectar pequeños volúmenes de muestra con bajas concentraciones de analito. Las características y propiedades de los sensores de pH se analizan con más detalle en [2-4]. Se muestra que la sensibilidad al pH de los materiales a granel de silicio es pobre. Se observaron buenas propiedades de detección de pH de los nanocables de Si (NW), con una sensibilidad de 58,3 mV / pH. Por ejemplo, en el campo del diagnóstico médico, las estructuras a nanoescala que tienen como objetivo la utilización de nanoestructuras de baja dimensión, como nanotubos de carbono, NW metálicos o semiconductores o nanocintas delgadas (NR) del tamaño de un átomo, pueden implementarse para una variedad de aplicaciones [5] . Entre las estructuras mencionadas, las estructuras de silicio NR y NW FET abren perspectivas para la detección de biomoléculas sin etiquetas, en tiempo real y de alta sensibilidad utilizando principios de unión basados ​​en afinidad [6]. Se estudió la sensibilidad de diferentes dimensiones de NR. Se demostró que el nuevo sensor con referencia integrada NR se puede utilizar para el monitoreo de errores en tiempo real durante la detección de pH [6]. Se agregan continuamente nuevas características y funciones a los dispositivos electrónicos, como los sistemas móviles de monitoreo de la salud y los dispositivos portátiles. A pesar del éxito de estos sistemas de control de la salud personal [7], se espera que la próxima generación de dispositivos portátiles incluya también un "laboratorio en un chip" portátil, un conjunto de biosensores médicos que se pueden utilizar para la detección y el diagnóstico de varios sustancias médicas [8, 9]. Para poder monitorear y detectar las primeras etapas de la enfermedad en un caso ideal a nivel de una sola molécula, el tamaño del transductor sensor debe ser comparable con los marcadores biológicos bajo prueba. Por lo tanto, deben desarrollarse biosensores basados ​​en NW y NR para el seguimiento de eventos biológicos que ocurren en dimensiones muy pequeñas. Otra área de aplicación importante es la optoelectrónica, donde la interacción de la luz con nanoestructuras puede utilizarse para futuras aplicaciones de dispositivos ópticos. Los diámetros de sub-longitud de onda y los efectos de proximidad pueden dar lugar a propiedades ópticas avanzadas, como baja reflectancia y, por tanto, alta absorción. Los resultados de la investigación de la absorción óptica de Si NW han demostrado los fuertes efectos dependientes del tamaño [10-12]. Los estudios de la absorción óptica de banda ancha mostraron un aumento de los espectros de absorción óptica total para las muestras de Si NW [13]. Los Si NW conducen a una reducción significativa de la reflectancia en comparación con las películas sólidas de silicio [13, 14]. La absorción óptica aumenta mientras que la longitud de onda disminuye. Cabe señalar que, a diferencia del material a granel, las estructuras de Si nanométricas pueden ser semiconductores de banda prohibida directa, lo que los convierte en una excelente opción para aplicaciones ópticas [11, 13, 15-18]. Por otro lado, la escala de tamaño aumenta la banda prohibida [15]. Esto puede resultar en un cambio exitoso de los espectros de absorción a longitudes de onda cortas [11, 18]. Con la disminución de tamaño, también deben tenerse en cuenta las limitaciones con respecto a la corriente y el voltaje. Para los dispositivos que operan a niveles de señal débiles, el ruido interno juega un papel crucial [4, 19, 20, 21]. Determina uno de los parámetros más importantes de los sensores:la relación señal / ruido (SNR). Como se muestra para los sensores SiNW de doble puerta, la sensibilidad del pH aumenta con el voltaje de la puerta del líquido y la SNR tiene un valor más alto (~ 10 ⁵ ) [11, 18]. El enfoque de nanocintas se abre a la fabricación CMOS a gran escala de chips de biomoléculas altamente sensibles para su uso potencial en medicina y biotecnología [22].

La investigación de vanguardia en materiales a nanoescala ha revelado que las propiedades electrónicas, magnéticas, térmicas y ópticas pueden diferir dramáticamente cuando se sintetizan sus formas unidimensionales. Los nanocables obtenidos mediante la utilización de cristales lamelares de uno o pocos átomos de espesor son formas novedosas de materiales a nanoescala unidimensionales y son sistemas ideales para investigar la dependencia del tamaño de las propiedades fundamentales.

En [23] se presenta un análisis detallado de los últimos logros en los métodos de síntesis y estudios teóricos de NR. En la literatura, no se han estudiado en detalle la fotoconductividad, la sensibilidad al pH, el ruido y los efectos de la longitud del canal en el mismo conjunto de matrices NW FET. Sin embargo, la rugosidad de la superficie y la contribución de las capas dieléctricas pueden cambiar considerablemente las propiedades de la estructura dependiendo de la tecnología de fabricación aplicada para diferentes conjuntos de dispositivos. En este sentido, comprender los efectos de la longitud del canal en el mismo conjunto de NW FET es importante para el desarrollo de dispositivos con funcionalidad avanzada.

El presente trabajo está dedicado al estudio de los FET basados ​​en nanocables de silicio, incluida la tecnología de fabricación de muestras y la caracterización de chips, sus características de corriente-voltaje (I – V) de luz y oscuridad y sensibilidad al pH. Se describen los efectos de la influencia de la longitud del canal sobre las corrientes fuente-drenaje, la sensibilidad del pH y el ruido de baja frecuencia. Demostramos que los nanocables de silicio, fabricados sobre la base de una fina capa de silicio sobre un sustrato de silicio oxidado, pueden tener una alta sensibilidad al pH bastante cercana al límite de Nernst.

Métodos / experimental

Las estructuras de silicio NW se fabricaron sobre la base de obleas de silicio sobre aislante (SOI) compradas a SOITEC. El proceso comienza con la oxidación térmica para formar máscaras duras de óxido de silicio de 20 nm de espesor. El espesor de la capa de silicio activo es de 50 nm. Luego, los NW de varias geometrías se modelan en una máscara dura utilizando litografía óptica y se transfieren en SiO ₂ capa usando el paso del proceso de grabado de iones reactivos. El patrón se utiliza para obtener nanocintas y nanocables de silicio mediante grabado químico húmedo en la solución de hidróxido de tetrametilamonio (TMAH). La capa dieléctrica de la compuerta, que también sirve como un canal de protección contra el ambiente líquido, es óxido de silicio de 8 nm de espesor crecido térmicamente. El canal NW era silicio casi sin dopar con una concentración de agujeros de aproximadamente 10 ¹⁵ cm ⁻³ . Los contactos de fuente y drenaje fueron altamente dopados para formar buenos contactos óhmicos. Para la conexión a la electrónica, los contactos de aluminio se modelaron mediante un proceso de despegue. Finalmente, las virutas se pasivaron con una capa de poliimida (PI) para proteger las líneas de alimentación de metal del entorno líquido. La Figura 1 muestra imágenes esquemáticas de las muestras en estudio en el modo de funcionamiento del sensor de pH (a) y el modo de funcionamiento del fotorreceptor (b), y la imagen SEM del NW investigado se presenta en la Fig. 2.

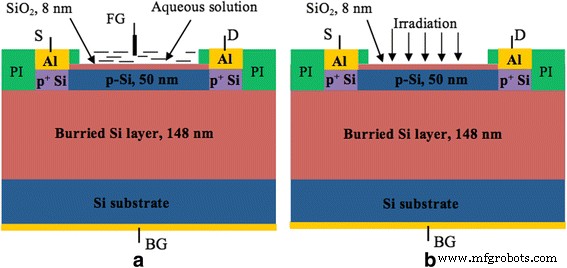
Estructuras de transistores de efecto de campo de nanocables de Si en estudio. Imagen esquemática de las muestras en estudio:pH:modo de funcionamiento del sensor ( a ) y modo de funcionamiento del fotorreceptor ( b ). Capa de poliimida PI, fuente S, drenaje D, puerta frontal FG (electrodo de referencia, RE), puerta trasera BG

Imagen SEM de la estructura Si NW FET. Imagen típica de micrografía electrónica de barrido (SEM) de una estructura de transistor de efecto de campo de nanocintas de Si fabricada

Resultados y discusión

Características de corriente-voltaje y sensibilidad al pH

Las figuras 3 y 4 muestran las características de corriente-voltaje (I – V) de fuente-drenaje de las muestras en estudio medidas a voltajes de puerta trasera de - 1 y - 5 V, correspondientemente. Las características se midieron en condiciones de oscuridad, así como bajo iluminaciones de potencia específicas de 0,85 y 1,6 W / cm ² a temperatura ambiente. La excitación de la luz se realiza mediante lámparas incandescentes ubicadas a una distancia de 15 cm del sensor. Las dependencias I – V demuestran un comportamiento típico que es similar a los FET de semiconductores de óxido de metal (MOSFET) [24] ya que las muestras bajo investigación tienen dimensiones relativamente grandes de l × w × t =(2 ÷ 10) × 10 × 0,05 μm ( l , w y t son la longitud, el ancho y el grosor del canal, correspondientemente). Las curvas I – V de las Figs. 3 y 4 pueden describirse como:

$$ {I} _ {\ mathrm {ds}} ={I} _ {\ mathrm {ds}, \ mathrm {d}} + {I} _ {\ mathrm {ds}, \ mathrm {ph}}, $$ (1)

donde yo _{ds, d} y yo _{ds, ph} son los componentes de corriente oscura y foto fuente-drenaje. La corriente oscura se puede describir mediante la conocida expresión de MOSFET para V _ds ≤ V _gs - V _th [24]:

$$ {I} _ {\ mathrm {ds}, \ mathrm {d}} =\ frac {w {\ mu} _n {C} _ {\ mathrm {ox}}} {l} \ left ({V} _ {\ mathrm {gs}} - {V} _ {\ mathrm {th}} - \ frac {V _ {\ mathrm {ds}}} {2} \ right) {V} _ {\ mathrm {ds}} . $$ (2)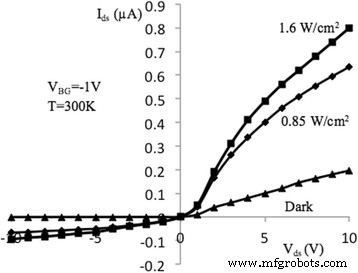

Características I – V de NW FET, medidas en excitación óptica ( V _BG =- 1 V). Características de corriente-voltaje de salida de la muestra NW FET con longitud l =10 μm, medido en la oscuridad y en la excitación por la potencia específica de la luz 0,85 y 1,6 W / cm ² , en T =300 K y V _BG =- 1 V

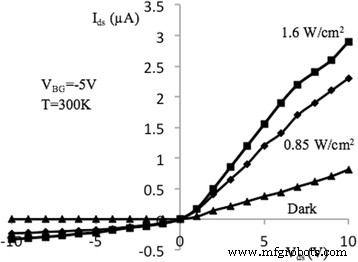
Características I – V de NW FET, medidas en excitación óptica ( V _BG =- 5 V). Características de corriente-voltaje de salida de la muestra NW FET con longitud l =10 μm, medido en la oscuridad y con excitación por la potencia específica de la luz 0,85 y 1,6 W / cm ² en T =300 K y V _BG =- 5 V

Aquí, C _buey = ε _buey / t _buey es la capacitancia de la capa de óxido por unidad de área, ε _buey y t _buey son la permitividad y el espesor de la capa de óxido de la puerta, μ _n es la movilidad de los electrones, y V _ds , V _gs y V _th son voltajes fuente-drenaje, puerta-fuente y umbral, correspondientemente. La tasa de generación de fotoportadores es igual a ηαN _ph , donde N _ph = W / hν es la intensidad de la irradiación. A niveles de inyección bajos y una vida útil constante de los orificios, la concentración de fotoportadores será \ (\ Delta p =\ eta \ alpha {\ tau} _p \ frac {W} {h \ nu} \) [25]. Los portadores se desvían a la tensión aplicada V _ds . En este caso, la fotocorriente se puede representar como:

$$ {I} _ {\ mathrm {ds}, \ mathrm {ph}} ={A} _ {\ mathrm {ch}} e {\ mu} _p \ Delta p \ frac {V_ {ds}} {l } ={A} _ {\ mathrm {ch}} e {\ mu} _p \ eta \ alpha {\ tau} _p \ frac {W} {h \ nu} \ frac {V _ {\ mathrm {ds}}} {l}. $$ (3)

Aquí, A _ch = peso es el área de la sección transversal del canal actual, e es la carga del electrón, ∆p y μ _p son la concentración y la movilidad del exceso de fotoportadores (huecos), α el coeficiente de absorción de iluminación, η el rendimiento cuántico, τ _p la vida del agujero, hν la energía del fotón y W la potencia específica de iluminación en [W / cm ² ].

En Eq. (3), asumimos que la intensidad del campo eléctrico se distribuye uniformemente a lo largo de la longitud del canal y el valor de A _ch varía ligeramente a lo largo del canal debido a la alta conductividad del canal. Cabe señalar que esta suposición es válida en la parte principal del canal, que está lejos de los contactos de fuente y drenaje.

A bajos voltajes V _ds , la corriente de drenaje de fuente I _ds crece aproximadamente linealmente con el voltaje. Con el aumento de la potencia específica de la luz, la magnitud de la I _ds aumenta. Las Figuras 5 y 6 muestran las curvas I – V del dispositivo investigado en los varios voltajes de la puerta frontal ( V _FG =- 1 V, - 5 V) medido en una solución acuosa con pH =6.2, 7 y 8.3. Podemos ver que aumentar el valor de pH da como resultado el aumento de la corriente del canal, I _ds . Esto concuerda bien con el modelo del contacto de la solución con la superficie de la capa de óxido, luego en la interfase óxido / solución se produjeron grupos hidroxilo SiOH. La concentración y el comportamiento de esos grupos hidroxilo dependen del valor del pH. El caso en el que la superficie no está cargada se llama punto de carga cero. Para el SiO ₂ capa dieléctrica, el punto se alcanza a pH =2,2. A valores de pH inferiores a 2,2, la superficie del óxido se carga positivamente; a valores más altos del pH, la superficie del óxido se carga negativamente. En el caso de una solución tampón con pH =7, la carga superficial de óxido de silicio se cargará negativamente. Por lo tanto, al potencial de puerta negativo aplicado, aumenta el valor absoluto de la carga negativa en el óxido superficial. Como resultado, la concentración de portadores mayoritarios aumenta en el canal de corriente (huecos en p-Si) y, por lo tanto, aumenta la corriente del canal.

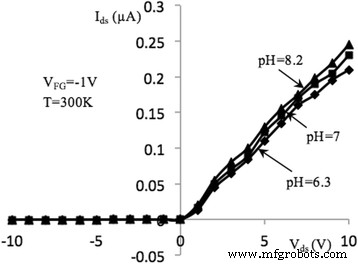
Características I – V de NW FET, medidas en diferentes soluciones de pH ( V _FG =- 1 V). Características de corriente-voltaje de salida de NW FET con longitud, l =10 μm, medido en la oscuridad y concentraciones de pH:6,3, 7, 8,2 en T =300 K, V _BG =- 5 V y V _FG =- 1 V

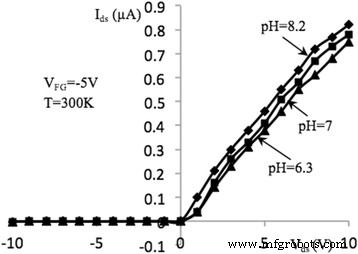
Características I – V de NW FET, medidas en soluciones de pH ( V _FG =- 5 V). Características de corriente-voltaje de salida de NW FET con longitud, l =10 μm, medido en la oscuridad y concentraciones de pH 6,3, 7, 8,2 en T =300 K, V _BG =- 5 V y V _FG =- 5 V

Las figuras 5 y 6 muestran las características I – V de las estructuras de Si NW que funcionan en modo de detección bioquímica. Las mediciones se realizaron cuatro veces para cada valor de pH. La repetibilidad estaba dentro del 7%. En [26], la sensibilidad al pH de los sensores bioquímicos se introdujo como

$$ {R} _ {\ mathrm {pH}} =\ frac {R _ {\ mathrm {ch}} \ Delta {I} _ {\ mathrm {ds}}} {\ Delta \ mathrm {pH}}. $$ (4)

Aquí, ∆I _ds y ∆pH son los cambios elementales en I _ds y pH. Tenga en cuenta que la sensibilidad al pH es el valor medible. En el medio de solución con el valor de pH aumentado, aumenta la corriente fuente-drenaje. Esto permite el registro de la variación de pH en cualquier biolíquido (dentro del rango de solución relevante para las soluciones fisiológicas) con alta precisión. Por ejemplo, para V _BG =- 5 V en el V _ds =5 V, la sensibilidad es igual a R _pH ≈ 56,4 mV / pH. En el V _BG =- 5 V, la sensibilidad del pH aumenta hasta 59,3 mV / pH y se acerca al límite de Nernst de 59,5 mV / pH [24]. La sensibilidad del pH aumenta con el aumento del voltaje de la puerta trasera. Por ejemplo, de las Figs. 5 y 6 en V _ds =8 V, obtuvimos la razón \ ({\ left ({R} _ {\ mathrm {pH}} \ right)} _ {V _ {\ mathrm {BG}} =- 5 \ \ mathrm {V}} / {(R)} _ {V_ {BG} =- 1 \ \ mathrm {V}} \ approx 5.17 \), es decir, una sensibilidad mejorada aproximadamente cinco veces.

Características y espectros de ruido de baja frecuencia causados ​​por cambios de irradiación y pH

Los espectros de ruido de las estructuras de Si NW se midieron a la corriente constante en el modo óhmico. La Figura 7 muestra la densidad espectral de potencia de ruido de la corriente de drenaje medida en condiciones de oscuridad, así como bajo irradiación con un voltaje de puerta trasera aplicado de V _BG =- 1 V en I _ds =0,1 μA. Los espectros de ruido, medidos en la oscuridad, demuestran 1 / f ^γ comportamiento del ruido con parámetro de ruido igual a γ =1. El nivel de ruido de baja frecuencia (LF) aumenta con el aumento de la intensidad de la irradiación de la luz. El aumento de la intensidad de la iluminación da como resultado el crecimiento de la concentración del portador principal. Esto a su vez provoca el crecimiento de las fluctuaciones de movilidad en el canal debido a una mayor interacción y tasas de dispersión como resultado de la dispersión, en primer lugar, entre los portadores y, en segundo lugar, entre los portadores y fonones acústicos, así como en diferentes trampas de impurezas [27].

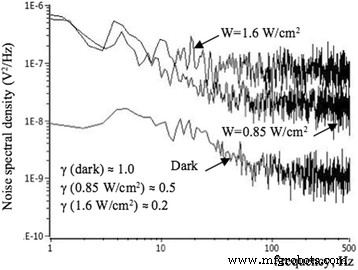
Espectros de ruido de NW FET, medidos en excitación óptica. Dependencia espectral del ruido LF, medida para la muestra NW FET con l =10 μm bajo iluminación:0,85 W / cm ² , 1,6 W / cm ² , y en la oscuridad; V _BG =- 1 V, T =300 K

Dado que las mediciones de ruido se realizaron a la corriente constante en el modo óhmico, la resistencia del canal cambia linealmente con el voltaje aplicado V _ds . Como se sabe, la densidad espectral de ruido 1 / f S _V es proporcional al voltaje en la potencia 2:

$$ {S} _V =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {ds}} ^ 2} {N {R} _ {\ mathrm {ch}} ^ 2 {f } ^ {\ gamma}} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {ds}} ^ 2} {p \ Omega {R} _ {\ mathrm {ch}} ^ 2 {f} ^ {\ gamma}} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {ds}} ^ 2} {R _ {\ mathrm {ch}} ^ 2 {f } ^ {\ gamma}} \ frac {e {\ mu} _p \ rho} {A _ {\ mathrm {ch}} l} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {ds}} ^ 2} {f ^ {\ gamma}} \ frac {e {\ mu} _p} {l ^ 2} \ frac {1} {R _ {\ mathrm {ch}}} \ propto \ frac { 1} {R _ {\ mathrm {ch}}}, \ kern1.75em \ frac {f ^ {\ gamma} {S} _V} {V _ {\ mathrm {ds}} ^ 2} \ propto \ frac {1} {R _ {\ mathrm {ch}}}. $$ (6)

Aquí, α _H es el parámetro Hooge, R _ch es la resistencia del canal actual; Ω = A _ch l es el volumen del canal actual; ρ es la resistencia específica del canal. La disminución de la resistencia del canal conduce al crecimiento de la densidad espectral del ruido. A la excitación ligera de una muestra de FET de nanocables con potencia W , tenemos:

$$ {\ Displaystyle \ begin {array} {l} {S} _ {V, L} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {d} \ mathrm {s} } ^ 2} {NR _ ​​{\ mathrm {ch}} ^ 2 {f} ^ {\ gamma}} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {d} \ mathrm { s}} ^ 2} {p \ Omega {R} _ {\ mathrm {ch}} ^ 2 {f} ^ {\ gamma}} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ { \ mathrm {d} \ mathrm {s}} ^ 2} {\ Omega {f} ^ {\ gamma}} \ frac {1} {p {\ left (\ rho l / {A} _ {\ mathrm {ch }} \ right)} ^ 2} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {d} \ mathrm {s}} ^ 2} {\ Omega {f} ^ {\ gamma}} \ frac {A _ {\ mathrm {ch}} ^ 2 {\ sigma} ^ 2} {pl ^ 2} =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {d } \ mathrm {s}} ^ 2} {A _ {\ mathrm {ch}} {lf} ^ {\ gamma}} \ frac {A _ {\ mathrm {ch}} ^ 2 {e} ^ 2p {\ mu} _p ^ 2} {l ^ 2} =\\ {} \ kern11.5em =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {d} \ mathrm {s}} ^ 2} {f ^ {\ gamma}} \ frac {A _ {\ mathrm {ch}}} {l ^ 3} {e} ^ 2 {\ mu} _p ^ 2 \ left ({p} _ {\ mathrm {d} } + \ Delta p \ right) =\ frac {\ alpha _ {\ mathrm {H}} {V} _ {\ mathrm {d} \ mathrm {s}} ^ 2} {f ^ {\ gamma}} \ frac {A _ {\ mathrm {ch}}} {l ^ 3} {e} ^ 2 {\ mu} _p ^ 2 \ left ({p} _ {\ mathrm {d}} + {\ eta \ alpha \ tau} _p \ frac {W} {h \ nu} \ right) \ end {array}} $$ (7)

Aquí, p _d es la concentración de agujeros en condiciones de oscuridad y σ es la conductividad específica. El nivel de ruido aumenta proporcionalmente a la intensidad de la iluminación.

Calculamos los valores del parámetro de ruido γ , utilizando las curvas presentadas en la Fig. 7. Se obtienen los siguientes parámetros para muestras, medidas en la oscuridad y con excitación luminosa de diferentes potencias:

γ (oscuro) ≈ 1.0, γ (0,85 W / cm ² ) ≈ 0.5 y γ (1,6 W / cm ² ) ≈ 0.2.

Bajo irradiación, el valor del parámetro de ruido γ disminuye. Esto se puede explicar de la siguiente manera. Al aumentar la potencia de la luz, aumenta la conductividad del canal de corriente. Como resultado, la vida útil de los portadores minoritarios τ _ef sube y alcanza valores τ _ef ≥ (10 ⁻³ ÷ 10 ⁻² ) s. Una vez que los pares de electrones y huecos se generan por absorción en silicio, se deben considerar varios mecanismos de recombinación. Estos procesos ocurren en paralelo y la tasa de recombinación es la suma de las tasas correspondientes al proceso individual. Varias vidas están asociadas con diferentes mecanismos de recombinación. La vida útil efectiva del portador tiene que ser determinada por la superficie del portador, radiativo, volumen (volumen) y el tiempo de vida de la recombinación Auger. Se sabe que el tiempo de vida radiativo es inversamente proporcional a la densidad del portador, y el tiempo de vida del Auger es inversamente proporcional al cuadrado de la densidad del portador [28]. La vida útil de la recombinación en masa está determinada por el mecanismo de recombinación de Shockley-Read-Hall. Es constante para densidades de portadoras de bajo nivel y aumenta para niveles de inyección altos [29,30,31]. Se sabe que la duración de la recombinación de la superficie es proporcional a la tasa de recombinación de la superficie e inversamente proporcional al espesor de la muestra [29, 32, 33].

El comportamiento de la vida útil será complejo, dependiendo de la densidad del portador en desequilibrio y los mecanismos de recombinación. A medida que aumenta la densidad de portadores, la vida útil efectiva puede ser una función constante o decreciente [29]. En los nanocables con una alta proporción de superficie a volumen, los estados de la interfaz de la superficie juegan un papel más importante y su contribución domina. Además, puede superar otros tipos de recombinación. Por otro lado, a un nivel moderado de densidad de portadores, la vida útil de la recombinación en masa también puede aumentar. Para nuestro caso de portadores de silicio NW, la vida útil efectiva está determinada básicamente por la recombinación de la superficie y el volumen y aumenta con el crecimiento de la densidad del portador.

Como se sabe, el ruido de recombinación de generación (g-r) tiene la forma de Lorentz [19, 34]:

$$ {S} _ {V, g-r} \ sim \ frac {1} {1 + {\ left (2 \ pi f {\ tau} _ {\ mathrm {ef}} \ right)} ^ 2}. $$ (8)

Aquí, f es la frecuencia. Está claro que la sección de la meseta sobre la dependencia S _{V , g - r} ( f ) está determinada por la condición

$$ 2 \ pi {f} _c {\ tau} _ {\ mathrm {ef}} \ le 1, $$ (9)

donde f _c es la frecuencia característica. Cabe señalar que con el aumento de la vida útil de los electrones, el valor de la frecuencia de corte f _c disminuye. La frecuencia característica del ruido g-r se desplaza a la región de baja frecuencia. Dado que la conductividad σ y de por vida τ _n aumenta al aumentar el poder de iluminación, la f _c disminuye al aumentar W , en consecuencia:

$$ {f} _c \ propto \ frac {1} {\ tau _ {\ mathrm {ef}}} \ propto \ frac {1} {W}. $$ (10)

Los procesos g-r conducen al apantallamiento del componente de ruido 1 / f bajo la meseta de ruido g-r. El hecho explica la disminución del valor del parámetro de ruido γ con un poder de iluminación cada vez mayor.

La Figura 8 ilustra la dependencia espectral del espectro de potencia de ruido LF de la muestra Si NW FET, medida en el V _FG =- 1 V, I _ds =0,1 μA en solución a los distintos valores de pH:6,3, 7,0 y 8,2. El parámetro de ruido disminuye con el aumento del valor de pH: γ (pH =6,3) ≈ 1,0; γ (pH =7,0) ≈ 0,5; γ (pH =8,2) ≈ 0,4. Las pendientes se calcularon en el rango de 10 a 500 Hz. El nivel de ruido de LF aumenta y su pendiente disminuye con el aumento del valor de pH. El aumento en el valor de pH conduce a una disminución en la resistencia del canal, que es causada por la acumulación de cargas negativas en la interfaz semiconductor-óxido. Disminución de la pendiente de S _V ( f ) La dependencia con el aumento del pH se puede explicar teniendo en cuenta el efecto del aumento de la conductividad del canal.

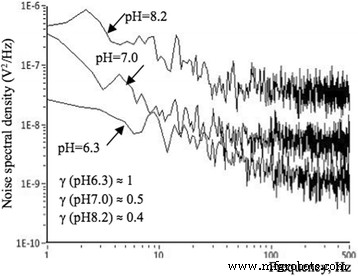
Espectros de ruido de NW FET, medidos en diferentes soluciones de pH. Dependencia espectral del ruido LF para NW con longitud, l =10 μm, medido a T =300 K y varios valores de pH:6,3, 7,0 y 8,2 a V _BG =- 5 V, V _FG =- 1 V

Efectos de la longitud del canal

En esta sección, presentamos los resultados de la influencia de la longitud del canal actual en los mecanismos de transporte, la sensibilidad del pH y también en el comportamiento del ruido LF de los sensores basados ​​en Si NW. La magnitud de la corriente es inversamente proporcional a la longitud del canal de corriente, lo que justifica la aplicación de la aproximación de deriva para el mecanismo de transporte, así como el supuesto de una distribución uniforme de la intensidad del campo eléctrico a lo largo del canal de corriente ( Figura 9). La influencia de la excitación de la luz conduce a un aumento en la magnitud de la corriente fuente-drenaje. La sensibilidad del pH aumenta con la longitud del canal actual y tiende al límite de Nernst de 59,5 mV / pH (Fig. 10), que concuerda bien con los valores obtenidos para los sensores de tamaño micro [27]. Nuestros resultados apoyan también las observaciones del comportamiento de la sensibilidad al pH obtenido para muestras de NW con diferentes geometrías [6]. El efecto de longitud estudiado sistemáticamente en nuestro trabajo se puede explicar de la siguiente manera. Dado que la longitud del canal l disminuye, el área de la superficie sensible al pH disminuye y, en consecuencia, el número de H ⁺ medibles iones en la solución acuosa disminuye. Según Eq. (2), el I actual _ds aumenta al disminuir l , que conduce a una disminución en la resistencia del canal de corriente a voltaje constante V _ds . Como la resistencia del canal R _ch disminuye, su modulación se ve obstaculizada bajo la influencia del H ⁺ iones por lo tanto, la sensibilidad al pH disminuye.

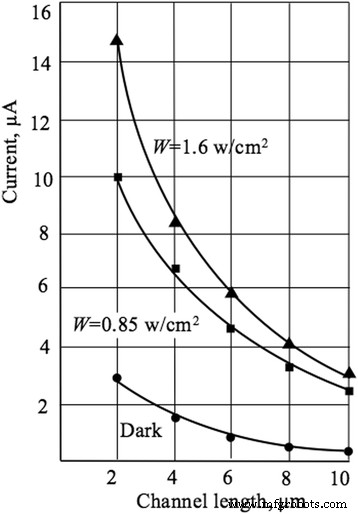
Corriente de canal de NW FET frente a longitud. Gráfico de la corriente del canal en función de la longitud del canal. V _BG =- 5 V, V _ds =- 5 V, R _ch =1,26 MΩ

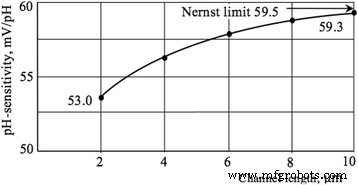
Sensibilidad al pH frente a longitud del canal. Gráfico de la sensibilidad del pH en función de la longitud del canal. V _FG =- 10 V, V _BG =- 5 V, V _ds =- 5 V, R _ch =1,26 MΩ

La Figura 11 ilustra la dependencia de la densidad espectral del ruido LF de la longitud del canal actual.

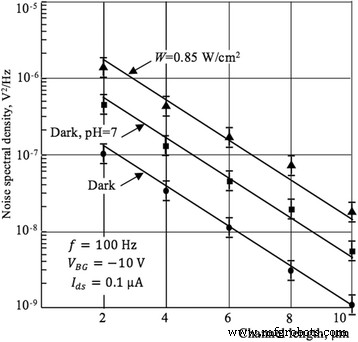
Densidad espectral de ruido frente a la longitud del canal actual. Gráfico de la densidad espectral de ruido en función de la longitud actual del canal. Para mediciones de pH V _FG =- 10 V

Estas curvas se trazan utilizando las dependencias espectrales del ruido LF medido para Si NW con diferentes longitudes en condiciones de oscuridad, bajo iluminación con una intensidad de 0,85 V / cm ² , y en una solución acuosa con un pH =7. El valor calculado de la pendiente de las curvas paralelas (Fig. 10) es igual a log (500/10) ≈ 2.7. Este valor está cerca del valor (igual a 3) obtenido teóricamente usando las Ecs. (6) y (7), S _V ∝ l ⁻³ con un error de alrededor del 10%. Los resultados demuestran que teóricamente predijo S _V ( l ) las dependencias concuerdan bien con las características medidas teniendo en cuenta el nivel relativamente alto de ruido térmico. Según Eq. (6), escalando la longitud del canal l hacia abajo conduce a la disminución de la resistencia y al aumento de la corriente, lo que corresponde al aumento de los portadores de carga en el canal. Esto, a su vez, da como resultado una mayor interacción de los portadores de carga con trampas en la interfaz entre el silicio y la capa dieléctrica. Thus, the noise level increases, which is also confirmed by experimental dependences (see Fig. 11).

The non-Nernstian pH-response of SiO₂ -gated FET-based sensors has been a major topic since the introduction of the ion-sensitive FET (ISFET) concept. The sensitivity of the SiNR FET sensor to changes in pH can be quantified by measuring the shift of the threshold voltage of the device and is defined by the Nernst equation [35]:

\( \frac{\delta {\Psi}_0}{\delta \mathrm{pH}}=-2.3\frac{kT}{q}\alpha \le 59\ \frac{mV}{\mathrm{pH}} \),

where δ Ψ₀ is the potential at the surface. The dimensionless parameter a which depends on the intrinsic buffer capacity of the oxide surface and the differential double-layer capacitance can be a value between 0 and 1.

Changes in the pH of the solution induce variations in the surface charge density and surface potential. It leads to a change in the NR channel conductance. In general, sensitivity is defined as the largest possible output response to a certain biological event. The pH sensitivity of BioFETs arises from the acid/base reactions at the oxide/electrolyte interface and the maximum pH response achievable by a conventional ISFET is the Nernst limit of 59 mV/pH. Over the years, there have been numerous reports [36,37,38,39,40,41,42,45] on devices with near Nernstian. The high sensitivity was achieved either by optimization of the intrinsic device transfer characteristics (such as lowering of the subthreshold swing or by tuning the gate potential) or by chemical surface modifications. Decreasing silicon thickness leads to higher surface charge sensitivity [45]. In [6], it is shown that at an optimum thickness of 30 nm the sensitivity reaches maximum value, and for a thicker device layer the pH response decreases and the largest response is obtained from the widest NR FET with the highest surface area. The most popular platform for chemical modification of SiO₂ surface is chemisorption of a few nanometer thick self-assembled monolayers [46], not only to enhance the pH sensitivity of Si/SiO₂ gated nanosensors [47], but also because biomolecules such as proteins [48] or DNA [49], which can be coupled to the other functional end of certain monolayers. Authors of Ref. [50] discussed the results concerning the functionalization and modification of SiNW FET sensors.

Conclusiones

Silicon nanowire FET biochemical sensors of various lengths were fabricated. The static dark and light-illuminated I–V curves as well as the behavior of these sensors in an aqueous solution with different values of pH are investigated. The static dark I–V dependencies demonstrate FET behavior. With increasing light intensity, the source-drain current grows because of the increase in the conduction of the current channel. The pH sensitivity increases with the increasing of the back-gate voltage and approaches to 59.5 mV/pH. The magnitude of the channel current is approximately inversely proportional to the length of the current channel and the pH sensitivity increases with increase of channel length approaching to the Nernst limit value, indicating that larger area devices are more suitable for the pH sensing.

The spectral density of the LF noise increases both under the action of the pH solution and the illumination, and in both cases, the frequency dependence of the noise is weakened and the value of the noise parameter γ decreases. With increasing of the pH value and illumination power, the 1/f-noise is screened by the g-r plateau. The characteristic frequency of the g-r noise component decreases with increasing illumination power. LF noise level increases and its slope decreases with increase of the pH value. It is shown that the measured value of the slope of noise spectral density dependence on the current channel length is 2.7 that is close to the theoretically predictable value 3 within 10% error.

Abreviaturas

FETs:

Field-effect transistors

LF:

Low-frequency

NWs:

Nanowires

TMAH:

Tetramethylammonium hydroxide

Aptasensor fluorescente a base de óxido de grafeno para la detección de encendido de CCRF-CEM Compuesto de nano fibras de TPU conductor de electricidad con alta capacidad de estiramiento para sensor de deformación flexible