Diseño y ajuste de la función de trabajo del grafeno mediante tamaño, modificación, defectos y dopaje:un estudio de teoría del primer principio
Resumen
En este trabajo, la función de trabajo (WF) de los grafenos, que se utilizan como dispositivos electrónicos, se ha diseñado y evaluado utilizando el enfoque del primer principio. Se consideraron diferentes estados del grafeno, como modificación de la superficie, dopaje y defectos. En primer lugar, WF depende en gran medida del ancho del grafeno prístino. Un ancho más grande conduce a un WF más pequeño. Además, los efectos de los hidroxilos, los defectos y las posiciones de los hidroxilos y los defectos son motivo de preocupación. El WF del grafeno modificado con hidroxilos es mayor que el del grafeno prístino. Además, el valor de WF aumenta con el número de hidroxilos. Las posiciones de los hidroxilos y los defectos que se desvían del centro tienen una influencia limitada en el WF, mientras que el efecto de la posición en el centro es sustancial. Por último, se eligen B, N, Al, Si y P como elementos de dopaje. El grafeno de tipo n dopado con átomos de N y P da como resultado una gran disminución en el WF, mientras que el grafeno de tipo p dopado con átomos de B y Al provoca un gran aumento en el WF. Sin embargo, el dopaje de Al en grafeno es difícil, mientras que el dopaje de B y N es más fácil. Estos descubrimientos proporcionarán un gran apoyo para la producción de dispositivos basados en grafeno.
Antecedentes
Como material que posee una variedad de excelentes rendimientos, el grafeno [1,2,3] ha sido ampliamente utilizado en diferentes áreas, como sensores, transistores de efecto de campo (FET), electrodos de dispositivos fotovoltaicos, diodos Schottky, tubos de vacío, y unión metal-semiconductor de diodos emisores de luz, y se ha convertido en un sustituto de muchos materiales [4, 5, 6, 7]. Los grafenos pueden resolver los problemas de miniaturización de FET y el costo de los dispositivos fotovoltaicos mientras mantienen una buena estabilidad y rendimiento eléctrico. Sin embargo, la función de trabajo del grafeno (WF) tiene una influencia crucial en el rendimiento de estos dispositivos electrónicos. Por lo tanto, conocer y controlar la WF de los grafenos es de gran importancia para los dispositivos electrónicos basados en grafeno. Generalmente, el rendimiento de los dispositivos FET se puede determinar mediante el WF de los electrodos fuente / drenaje [8,9,10]. Con las diferencias en WF de los materiales después del contacto metal-semiconductor, existirá una diferencia de potencial en la interfaz, que tiene un efecto directo sobre el contacto Schottky u óhmico [10]. Dado que la alineación de la banda de dos materiales diferentes está determinada por sus respectivos WF, controlar el WF de grafeno es la clave para reducir las barreras de contacto [11].
La WF de grafeno medida a través del experimento es aproximadamente de 4,2 a 4,8 eV [12, 13]. El cambio de nivel de Fermi conducirá al cambio de WF. Muchos experimentos y análisis teóricos demostraron que el nivel de Fermi de grafenos se puede ajustar mediante el dopaje deliberado con moléculas aromáticas y de gas [14, 15] o irradiación ultravioleta [16], funcionalización de la superficie [17, 18], defectos [19] y electrostática. puerta [20]. Por ejemplo, Yuan et al. encontraron que los WF del grafeno cambian drásticamente a través de la adsorción de Na y Cl [21]. Zhang y col. demostraron que el WF puede ajustarse con precisión dentro del rango de 4.0 a 4.5 eV cubriendo el grafeno con cationes de metales alcalinos [22]. Leenaerts y col. aprendió las características intrínsecas del grafeno. Los resultados mostraron que la WF de pocas capas de grafeno era casi independiente del número de capas, pero puede ser modulada por la capa dipolar [23]. Volodin y col. y Peng et al. utilizó el método mecánico para cambiar el grafeno WF [24]. Todos ellos encontraron que el WF aumentará con la tensión. Yu y col. utilizaron efectos de campo eléctrico para ajustar la WF del grafeno y demostraron que la WF puede ajustarse dentro del rango de 4.5–4.8 eV para grafenos monocapa y 4.65–4.75 eV para grafenos bicapa en condiciones ambientales y de nitrógeno seco [25]. Shi y col. encontraron que el potencial de superficie de las películas de grafeno se puede ajustar controlando el tiempo de inmersión. Para un tiempo de dopaje inferior a 20 s, el potencial de superficie se incrementó monótonamente a aproximadamente 0,5 V [13]. Además, se descubrió que la irradiación es un método eficaz para controlar la concentración de dopaje. Stratakis y col. controló los niveles de dopaje y reacción para adaptar el WF de las capas de GO-Cl de 4,9 eV a un valor máximo de 5,23 eV ajustando el tiempo de exposición al láser [26]. Sin embargo, Kang et al. sintonizó el WF del óxido de grafeno a través de la funcionalización directa de la superficie [27].
Aunque muchos estudios anteriores han informado métodos para controlar el grafeno WF, los resultados de la investigación no son lo suficientemente completos. Por ejemplo, el estudio comparativo sobre el efecto de tamaño de diferentes grafeno quirales en WF no proporciona suficiente información. Además, los efectos de las modificaciones y defectos del grafeno en WF aún no están muy claros. Aunque se estudió el efecto del dopaje sobre el grafeno WF, no se mencionó la energía de formación correspondiente de los átomos de dopaje. Por ejemplo, en el experimento de Shi, el grafeno se sumergió en un AuCl 3 solución para ajustar el WF [13]; sin embargo, la relación entre la WF y la concentración de dopaje aún no estaba clara. Además, debe tenerse en cuenta que aún no se han informado los impactos de las posiciones de los grupos funcionales y los defectos en el grafeno WF. Dado el alto costo de los métodos de control de WF, se deben investigar las características intrínsecas de los diferentes métodos.
En este artículo, se investigó un estudio exhaustivo sobre los métodos de control de la WF a través de la teoría del primer principio. Los efectos del dopaje y las posiciones de los hidroxilos y los defectos se informaron y destacaron primero. Primero, se consideraron los grafenos con diferente quiralidad (zigzag y sillón), y se investigó la dependencia de WF en el ancho del grafeno. En segundo lugar, se calcularon los WF del grafeno con modificaciones superficiales y defectos. Primero se compararon diferentes distribuciones de hidroxilos, seguidas del efecto de los defectos en varias posiciones. En tercer lugar, se eligieron B, N, Al, Si y P como elementos de dopaje para estudiar el efecto de dopaje de los WF.
Métodos
Todos los cálculos se realizaron en código CASTEP basado en la teoría funcional de la densidad (DFT) [28], que es una especie de investigación de la mecánica cuántica para la estructura electrónica del sistema de múltiples electrones. La DFT se ha utilizado ampliamente en el estudio de las propiedades físicas y químicas, incluidos los nanomateriales de grafenos y nanotubos de carbono [29, 30]. DFT también puede simular con precisión decenas a cientos de sistemas atómicos y describir el átomo como partículas cuánticas, es decir, el conjunto de núcleos y electrones [31].
La aproximación de gradiente generalizada (GGA) y la aproximación de densidad local (LDA) son las funciones de intercambio-correlación comúnmente utilizadas en los cálculos de mecánica cuántica. Se describen en las Ecs. (1) y (2):
$$ {E} _ {\ mathrm {xc}} \ \ left [\ rho \ right] =\ int {f} _ {\ mathrm {xc}} \ left [\ \ rho \ left (\ boldsymbol {r} \ right), | \ Delta \ rho \ left (\ boldsymbol {r} \ right) \ | \ right] d \ boldsymbol {r} $$ (1) $$ {E} _ {\ mathrm {xc}} \ \ left [\ rho \ right] =\ int d \ boldsymbol {r} \ \ rho \ left (\ boldsymbol {r} \ right) \ {\ varepsilon} _ {\ mathrm {xc}} \ \ left [\ rho \ left (\ boldsymbol {r} \ right) \ right] $$ (2)donde R Yo y r son las coordenadas del núcleo atómico y el electrón, respectivamente. La energía de intercambio-correlación en un gas de electrones no homogéneo se reemplaza por la E xc [ ρ ] en gas de electrones uniforme. Tanto GGA como LDA se han utilizado para los cálculos en materiales bidimensionales. Lebègue y col. encontraron que la estructura de bandas de materiales bidimensionales obtenidos utilizando LDA o GGA es muy similar [32]. Al mismo tiempo, GGA se utilizó en el cálculo de las propiedades eléctricas del grafeno en las investigaciones de Kharche y Gui, lo que garantiza la precisión [33, 34].
En cuanto a la WF, los estudios anteriores basados en sondas de barrido habían demostrado que la WF se mide en 4,6 eV, como con el grafito [35]. Generalmente, los WF en el rango de 4,6 a 4,9 eV son aceptables [36, 37]. Además, LDA [38] y GGA [39] predijeron la WF como 4,48 y 4,49 eV, respectivamente. En comparación con la fecha del experimento, el WF calculado por la teoría es ligeramente menor. GGA se ha unido a un gradiente de densidad no local y su no localidad es más adecuada para procesar la falta de homogeneidad de la densidad, pero LDA funciona mejor en un sistema de apilamiento. Por lo tanto, en los cálculos de WF y propiedad eléctrica del grafeno, se eligió GGA en este estudio teórico. Además, en este cálculo, la distancia de vacío se establece en 15 Å de modo que las interacciones electrostáticas entre dos lados de una losa son despreciables y el potencial electrostático alcanza su valor asintótico. El pseudopotencial ultra suave se utiliza para describir la interacción entre electrones e iones. La energía de corte es de 340 eV, la zona de Brillouin se muestrea usando una cuadrícula de puntos k de Monkhorst-Pack de 9 × 9 × 1 [40], y la mancha de Methfessel-Paxton [41] es de 0,05 eV. El criterio de convergencia de la energía de campo autoconsistente fue 1.0 × 10 −6 eV, y la fuerza MAX es 0.03 eV / Å.
Resultados y discusión
WF de grafenos en zigzag y sillón con diferentes tamaños
En términos generales, WF se puede definir como la energía mínima necesaria para extraer un electrón del volumen al infinito [42]. Como en los cálculos de mecánica cuántica, WF se define como la diferencia entre el nivel de vacío ( V 0 ) y el nivel de Fermi ( E f ), como se muestra en la Ec. (3):
$$ \ mathrm {WF} ={V} _0- {E} _ {\ mathrm {f}} $$ (3)Los cálculos CASTEP para superficies de cristal se realizan en losas con una región de vacío. Efectivamente, una matriz infinita de losas de material periódicas 2D está separada por amplios espacios de vacío. CASTEP produce la energía de Fermi para tales sistemas y la distribución espacial del potencial electrostático [43]. El grafeno con diferentes anchos tiene varias propiedades. Los modelos con diferente quiralidad de zigzag y sillón fueron elegidos para dilucidar el efecto del ancho en el WF. En este cálculo, se calcularon muestras con el rango de celdas de una a siete unidades. La figura 1 ilustra la definición del tamaño de los grafenos en zigzag y sillón. La orientación del cristal de los grafenos en zigzag y de sillón es diferente; la estructura cristalina del grafeno en zigzag es rómbica pero la estructura cristalina del grafeno de sillón es dimetrica, como se muestra en la Fig. 1a, b. El ancho del grafeno se define en la dirección horizontal y la longitud del grafeno se define en la dirección vertical. Además, una celda unitaria se establece como un anillo de carbono.
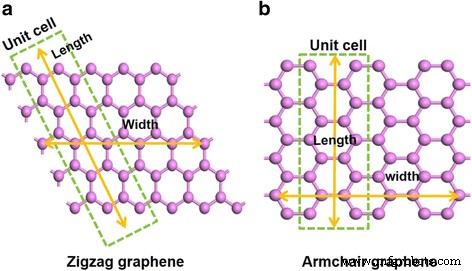
La definición del tamaño del grafeno. Las estructuras esquemáticas de zigzag ( a ) y sillón ( b ) grafenos que ilustran la definición del tamaño del grafeno. Una celda unitaria se establece como un anillo de carbono en el cuadro verde. Las flechas amarillas representan la dirección del ancho y el largo
La banda prohibida del grafeno cambia con el cambio de ancho del grafeno. En términos generales, el grafeno en zigzag presenta una propiedad metálica y el grafeno de sillón presenta una propiedad semimetálica. Sin embargo, ¿cuál es la relación entre WF y ancho en grafenos? La Figura 2 muestra la relación entre el tamaño del grafeno y el WF. La longitud y el ancho de los grafenos son desiguales en la Fig.2a en la que la longitud se establece constantemente como celdas de siete unidades, pero el ancho se organiza desde celdas de una unidad a siete unidades (1 × 7 a 7 × 7), mientras que el la longitud y el ancho son iguales en la Fig. 2b, en la que el tamaño se organiza desde supercélulas de 2 × 2 a supercélulas de 7 × 7. La WF se ve muy afectada por el ancho del grafeno. Generalmente, con el aumento del tamaño del grafeno, el WF disminuye. Además, el WF de los grafenos en zigzag es siempre mayor que el de los grafenos de sillón. Sugerimos que este fenómeno es causado por la estructura cristalina del grafeno. De hecho, la orientación del cristal tiene un gran impacto en el rendimiento de los materiales. La estructura cristalina del grafeno en zigzag es una estructura de cubo, mientras que la estructura cristalina del grafeno del sillón es una estructura de diamante. Comparando el WF entre las Fig. 2a, b, el WF de los grafenos (el grafeno en la Fig. 2a) con el ancho y la longitud desiguales sería mayor que el del grafeno (el grafeno en la Fig. 2b) con el mismo ancho y longitud. El gradiente de reducción del WF en la Fig. 1a también es mayor. Además, la diferencia de WF entre las supercélulas 6 × 6 y 7 × 7 en el sillón y los grafenos en zigzag es pequeña; creemos que el WF se mantendrá estable cuando el tamaño del grafeno sea de hasta las supercélulas de 6 × 6.
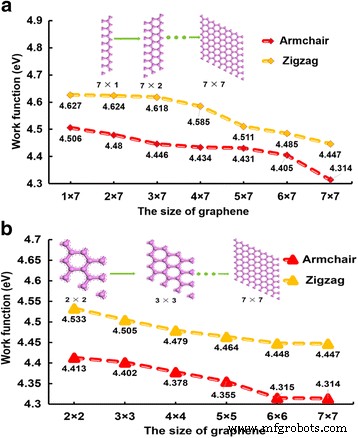
La relación entre el tamaño del grafeno y la WF. La relación entre el tamaño del grafeno y la WF. La longitud y el ancho de los grafenos son diferentes en ( a ), mientras que lo mismo en ( b )
También se analizaron los intervalos de banda de los grafenos con varios anchos, como se enumera en la Tabla 1. En general, los grafenos con un tamaño pequeño tendrán un intervalo de banda pequeño. Sin embargo, a medida que aumenta el ancho, la banda prohibida disminuyó o incluso se cerró [44]. Son et al. han demostrado que las nanocintas de grafeno con bordes homogéneos en forma de sillón o en zigzag tienen huecos de energía que disminuyen a medida que aumentan los anchos del sistema [45]. La Tabla 1 también muestra que la banda prohibida disminuyó con el tamaño del grafeno. En general, la banda prohibida de los grafenos de sillón es más pequeña que la de los grafenos en zigzag. Los grafenos con ancho y largo desiguales también poseen una banda prohibida más grande que los grafenos con el mismo ancho y largo.
Efectos de los hidroxilos, defectos y posiciones de los hidroxilos y defectos en el WF
La funcionalización siempre se toma como un método de modificación en el diseño y mejora del rendimiento del material de destino; la hidroxilación es uno de estos métodos. Se analiza la influencia de la cantidad y la posición de los hidroxilos y los defectos en el WF, como se muestra en la Fig. 3. Los recuadros (a) y (b) ilustran los diagramas de estructura del hidroxilo y las posiciones de los defectos en el grafeno, respectivamente. En este cálculo, se seleccionan grafenos en zigzag prístinos con un tamaño de supercélula de 4 × 4, y la WF calculada es 4,479 eV, que es ligeramente más pequeña que la del resultado del experimento [12]. La modificación de hidroxilo dará como resultado un aumento de WF. Kang y col. determinó que el valor de WF del óxido de grafeno a través del experimento fue de 4,91 eV [27]. Sin embargo, no se informó el número de grupos funcionales y sus posiciones. El WF de los grafenos en zigzag con un hidroxilo que calculamos es 4.504 eV, que es mayor que el de los grafenos en zigzag prístinos. Junto con el aumento de los hidroxilos, aumenta la WF. Además, el incremento es relativamente grande; la WF máxima alcanza los 5,102 eV. Este resultado se debe al efecto hidroxilo, que se destaca con el número creciente de hidroxilos. Además, se eligen cuatro hidroxilos para analizar el efecto de la distribución de grupos funcionales sobre el WF. El recuadro (a) da cuatro formas diferentes de distribuir los hidroxilos; las distribuciones son simétricas. Con una distribución intensiva, el WF es grande. Sin embargo, con una distribución dispersa, el WF es pequeño. El valor máximo de WF es 4.829 eV, mientras que el valor mínimo de WF es 4.658 eV. Este fenómeno debería ser causado por el efecto de agregación de los hidroxilos. Además, se investigan cuatro sitios de defectos diferentes en el grafeno 4x4, como se muestra en el recuadro (b). En general, los defectos darán como resultado la disminución del grafeno WF. Bae y col. mostró que el grafeno WF era más pequeño cuando existía la vacante. Y cuanto menor era la tasa de defectos, menor era el WF [46]. La WF del grafeno con el defecto en el centro es 4.337 eV, mientras que la WF del grafeno con el defecto desviado del centro es mayor a 4.363 eV, que es ligeramente más pequeña que la del grafeno en zigzag prístino 4 × 4. Esta diferencia significa que los defectos en el centro tienen más impacto en la estructura, por lo que el WF es mínimo. Por lo tanto, sugerimos que los sitios de defectos centrales tienen un gran efecto sobre el WF, mientras que los defectos desviados del centro tienen un efecto menor. Kim y col. descubrió que el dopaje de agujeros conduce a una diferencia en el WF de hasta 400 meV, lo cual es consistente con lo que estamos calculando [47].
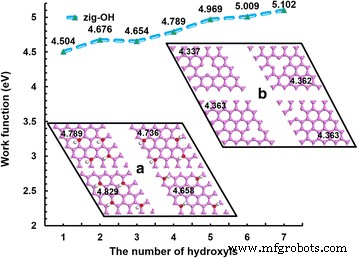
La relación entre el WF y el número de hidroxilos. La relación entre el WF y el número de hidroxilos; el tamaño del grafeno se establece en supercélulas de 4 × 4. Las imágenes insertadas presentan cuatro modos de distribución diferentes de hidroxilos ( a ) y defectos ( b )
Efecto de los dopantes de B, N, Al, Si y P en el WF
El dopaje es una forma eficaz de controlar la WF, la banda prohibida y las propiedades de adsorción. Por tanto, en este estudio se investigan los efectos y las concentraciones del dopaje. La Figura 4 muestra el efecto de diferentes dopantes sobre el WF; el tamaño del grafeno es de 4 × 4 supercélulas. Los dopantes de 1, 2, 3, 4, 5 y 6 átomos responden a las concentraciones de 2,4, 4,9, 7,3, 9,8, 12,2 y 14,6%, respectivamente. El efecto de los dopantes en el WF es significativo y sigue una cierta tendencia. En primer lugar, el WF de todos los grafenos dopados disminuye a medida que aumenta la concentración, excepto el grafeno dopado con B, que muestra un efecto opuesto. Legesse y col. También encontraron que el WF del grafeno dopado con metales alcalinos disminuye con el aumento de la concentración [48]. En segundo lugar, el incremento del WF en el grafeno dopado con B y Al es relativamente mayor que el de los otros grafenos. Al comparar el valor de WF, los grafenos de tipo p dopados con B y Al tienen un WF más grande, y el valor máximo es de hasta 5,148 eV para el grafeno dopado con B a una concentración del 14,6%. Por el contrario, el WF es mucho más pequeño en los grafenos de tipo n dopados con N y P; el valor mínimo se reduce a 3,23 eV a una concentración del 14,6% en grafeno dopado con P. Kwon y col. también mostró que los p-dopantes aumentarían la WF de grafeno de 4,2 a 5,14 eV [49]. Kvashnin y col. también demostró el fenómeno de que el dopaje B causaría un aumento de WF, pero el dopaje N y P resultó en una disminución de WF [19, 50]. Además, el WF de los grafenos dopados con Si es relativamente estable. Esto puede deberse al hecho de que los átomos de C y Si son congéneres. Por lo tanto, sugerimos que el dopaje de tipo p conduciría a un aumento de la WF; sin embargo, la cantidad está determinada por los elementos de dopaje. El WF tiende a ser estable a una concentración del 14,6%. Por otro lado, el dopaje de tipo n hará que la WF disminuya drásticamente.
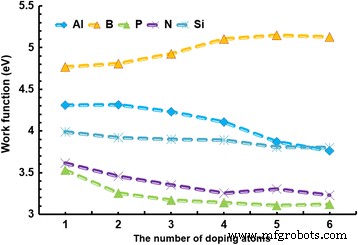
La relación entre el WF y el número de átomos de dopaje. La relación entre el WF y el número de átomos de dopaje. Diferentes tipos de dopantes, por ejemplo, Al, B, P, N y Si, se dopan en el grafeno con el tamaño de 4 × 4 células
Aunque se ha analizado la influencia de los dopantes en el WF y tiene una importancia vital para la aplicación del grafeno, la viabilidad del dopaje para varios átomos es diferente. Por lo tanto, calculamos la energía de formación de diferentes átomos de dopaje en GNR. La energía de formación [51] se describe como Eq. (4):
$$ {E} _ {\ mathrm {formación}} ={E} _ {\ left (\ mathrm {GNRs} + d \ right)} + {nE} _ {\ mathrm {C}} - {E} _ {\ left (\ mathrm {GNRs} \ right)} - {nE} _ {\ mathrm {d}} $$ (4)donde E formación es la energía de formación, E (GNR) es la energía de los GNR prístinos, E (GNRs + d ) es la energía de los GNR dopados, d es el átomo de dopaje, n es el número y E C y E d son los potenciales químicos determinados para los átomos de carbono y de dopaje.
La energía de formación se puede utilizar para evaluar si la viabilidad de utilizar átomos para el dopaje es buena o no. Cuanto menor sea la energía de formación, más fácil será el dopaje. La Figura 5 muestra que el grafeno dopado con Al tiene la energía de formación más grande pero más inestable; el aumento de los átomos de Al conduce a cambios drásticos en la estructura del grafeno con un tamaño de 4 × 4 células. Por el contrario, la energía de formación de B y N es muy pequeña, pero los pequeños cambios son evidentes con el aumento del número de átomos. Los átomos de Al, Si y P tienen más fluctuaciones en la energía de formación en comparación con los átomos de B y N. Esto se debe a que las energías de formación de Al, Si y P en el grafeno son grandes, lo que significa que el Al-, Si - y los grafenos dopados con P son menos estables, especialmente el grafeno dopado con Al tiene la estructura más inestable. Son relativamente difíciles de dopar con grafeno. En general, el dopaje con Al en grafeno es difícil, mientras que el dopaje B y N es más fácil. La WF y la energía de formación de estos dopantes en grafeno se registran en la Tabla 2.
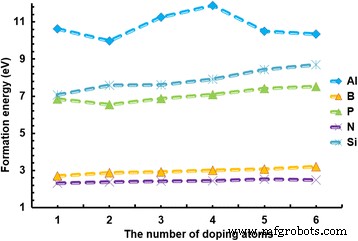
La relación entre la energía de formación y el número de átomos de dopaje. La relación entre la energía de formación y el número de átomos de dopaje. Diferentes tipos de átomos de dopaje, por ejemplo, Al, B, P, N y Si, se dopan en el grafeno con tamaños de celda de 4 × 4
Conclusiones
En este estudio se investiga la WF del grafeno en diferentes estados, como la modificación de la superficie, el dopaje y los defectos. Básicamente, el WF disminuye a medida que aumenta el ancho del grafeno. Para la modificación de hidroxilo, el WF es grande cuando aumenta el número de hidroxilos. Además, cuando la distribución de hidroxilos es intensa, la WF también aumenta. El defecto disminuiría la WF de grafeno, que no depende de las posiciones. El dopaje tipo p con B y Al llevaría a aumentar la WF; sin embargo, la cantidad aumentada viene determinada por los dopantes. El dopaje de tipo n con N y P reduce enormemente la WF. Estos descubrimientos proporcionarán un apoyo teórico para controlar el grafeno y mejorar aún más el diseño de dispositivos basados en grafeno.
Nanomateriales
- Las 3 etapas de la impresión 3D y cómo funcionan
- ¿Qué es la computación en la nube y cómo funciona?
- Diseño generativo e impresión 3D:la fabricación del mañana
- Bluetooth 5.1 SoC está diseñado para reducir el tamaño y el costo del diseño
- Los entresijos de una solicitud de trabajo de mantenimiento
- Estudio de los primeros principios sobre la estabilidad y la imagen STM del borofeno
- Ajuste de las morfologías de la superficie y las propiedades de las películas de ZnO mediante el diseño de la capa interfacial
- Estudio experimental sobre las características de flujo y transferencia de calor de nanofluidos de agua-TiO2 en un tubo estriado en espiral
- Estudio sobre la memoria de conmutación de resistencia multinivel y el fotovoltaje dependiente del estado de la memoria en uniones Pt / Nd:SrTiO3
- La robótica y el futuro de la producción y el trabajo
- Nuevo estudio:impacto del COVID-19 en el futuro del trabajo y la automatización



