MATLAB - Integración
La integración se ocupa de dos tipos de problemas esencialmente diferentes.
-
En el primer tipo, se da la derivada de una función y queremos encontrar la función. Por lo tanto, básicamente invertimos el proceso de diferenciación. Este proceso inverso se conoce como antidiferenciación, encontrar la función primitiva o encontrar una integral indefinida .
-
El segundo tipo de problemas implica sumar un número muy grande de cantidades muy pequeñas y luego tomar un límite a medida que el tamaño de las cantidades se aproxima a cero, mientras que el número de términos tiende a infinito. Este proceso conduce a la definición de la integral definida .
Las integrales definidas se utilizan para encontrar el área, el volumen, el centro de gravedad, el momento de inercia, el trabajo realizado por una fuerza y en muchas otras aplicaciones.
Encontrar la integral indefinida usando MATLAB
Por definición, si la derivada de una función f(x) es f'(x), entonces decimos que una integral indefinida de f'(x) con respecto ax es f(x). Por ejemplo, dado que la derivada (con respecto a x) de x 2 es 2x, podemos decir que una integral indefinida de 2x es x 2 .
En símbolos −
f'(x 2 ) =2x , por lo tanto,
∫ 2xdx =x 2 .
La integral indefinida no es única, porque la derivada de x 2 + c, para cualquier valor de una constante c, también será 2x.
Esto se expresa en símbolos como −
∫ 2xdx =x 2 + c .
Donde, c se llama una 'constante arbitraria'.
MATLAB proporciona un int Comando para calcular la integral de una expresión. Para derivar una expresión para la integral indefinida de una función, escribimos −
int(f);
Por ejemplo, de nuestro ejemplo anterior −
syms x int(2*x)
MATLAB ejecuta la instrucción anterior y devuelve el siguiente resultado −
ans = x^2
Ejemplo 1
En este ejemplo, encontremos la integral de algunas expresiones de uso común. Cree un archivo de script y escriba el siguiente código en él −
syms x n int(sym(x^n)) f = 'sin(n*t)' int(sym(f)) syms a t int(a*cos(pi*t)) int(a^x)
Cuando ejecuta el archivo, muestra el siguiente resultado −
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a)
Ejemplo 2
Cree un archivo de script y escriba el siguiente código en él −
syms x n int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))
Tenga en cuenta que el bonito función devuelve una expresión en un formato más legible.
Cuando ejecuta el archivo, muestra el siguiente resultado −
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2
Encontrar la integral definida usando MATLAB
Por definición, la integral definida es básicamente el límite de una suma. Usamos integrales definidas para encontrar áreas como el área entre una curva y el eje x y el área entre dos curvas. Las integrales definidas también se pueden usar en otras situaciones, donde la cantidad requerida se puede expresar como el límite de una suma.
El int La función se puede utilizar para la integración definitiva pasando los límites sobre los que desea calcular la integral.
Para calcular
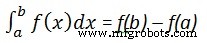
escribimos,
int(x, a, b)
Por ejemplo, para calcular el valor de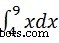 
escribimos −
int(x, 4, 9)
MATLAB ejecuta la instrucción anterior y devuelve el siguiente resultado −
ans = 65/2
A continuación se muestra el equivalente en octavas del cálculo anterior −
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));
Octave ejecuta el código y devuelve el siguiente resultado −
Area: 32.500
Se puede dar una solución alternativa usando la función quad() proporcionada por Octave de la siguiente manera −
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));
Octave ejecuta el código y devuelve el siguiente resultado −
Area: 32.500
Ejemplo 1
Calculemos el área encerrada entre el eje x y la curva y =x 3 −2x+5 y las ordenadas x =1 y x =2.
El área requerida está dada por −
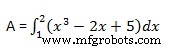
Cree un archivo de script y escriba el siguiente código −
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));
Cuando ejecuta el archivo, muestra el siguiente resultado −
a = 23/4 Area: 5.7500
A continuación se muestra el equivalente en octavas del cálculo anterior −
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));
Octave ejecuta el código y devuelve el siguiente resultado −
Area: 5.7500
Se puede dar una solución alternativa usando la función quad() proporcionada por Octave de la siguiente manera −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));
Octave ejecuta el código y devuelve el siguiente resultado −
Area: 5.7500
Ejemplo 2
Encuentra el área bajo la curva:f(x) =x 2 cos(x) para −4 ≤ x ≤ 9.
Cree un archivo de script y escriba el siguiente código −
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
Cuando ejecuta el archivo, MATLAB traza el gráfico −
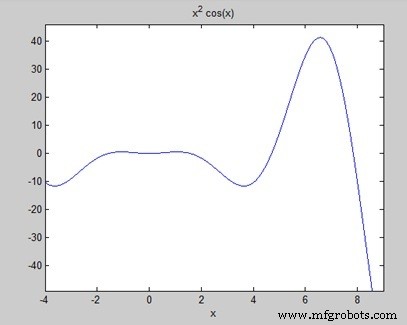
La salida se da a continuación −
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
A continuación se muestra el equivalente en octavas del cálculo anterior −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));
MATLAB