Estabilidad de forma de nanoplacas metálicas:un estudio de dinámica molecular

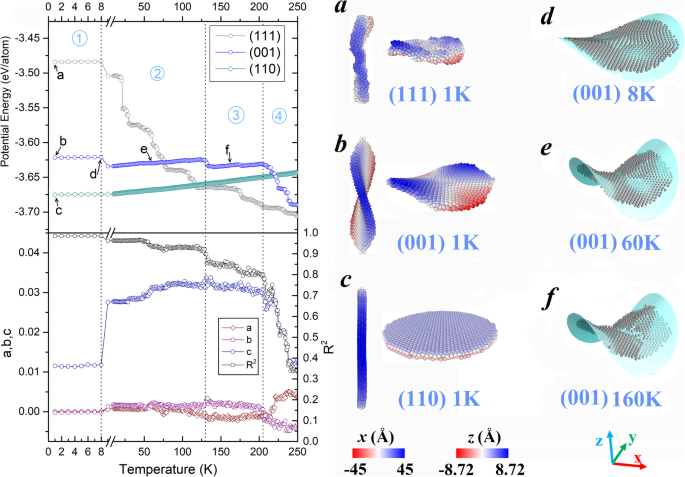
Panel izquierdo:Evolución de la temperatura de la energía potencial de tres nanoplacas (gráficos superiores) y los parámetros geométricos obtenidos al ajustar la capa media de la nanoplaca (001) (gráficos inferiores); Panel derecho: a , b , c Instantáneas de tres nanoplacas después de la relajación. d , e , f Instantáneas de la capa intermedia en la nanoplaca (001) tomadas a temperaturas representativas. Las superficies cian indican los resultados de ajuste correspondientes

Para investigar cuantitativamente la variación morfológica, ajustamos la capa media de la nanoplaca (001) mediante la ecuación de superficie cuádrica z =A x ² + B y ² + C xy + D. Los resultados del ajuste se proporcionan debajo de los gráficos de energía en la Fig.1, en los que a, byc son los parámetros geométricos en la ecuación, y R ² se refiere al coeficiente de determinación. R ² indica el grado de ajuste, y su valor ideal es igual a 1. De acuerdo con las variaciones de energía, las transiciones correspondientes de estos parámetros de ajuste también se observan en los puntos críticos entre las diferentes etapas. Las temperaturas críticas se identifican en 8, 129 y 205 K. Durante las primeras tres etapas, el valor de R ² permanece por encima de 0,8, lo que implica que la nanoplaca (001) mantiene aproximadamente su forma de silla de montar. Dado que el parámetro c es obviamente mayor que ayb, las dos secciones elevadas de la nanoplaca están orientadas a lo largo de la dirección [110]. Mientras tanto, el valor de c aumenta significativamente después de la primera etapa, lo que sugiere la notable curvatura de la superficie hacia arriba. Esta tendencia se puede percibir claramente a partir de las instantáneas representativas en la Fig. 1d-f, que se toman respectivamente a 8, 60 y 160 K. Cada deformación por flexión saca al sistema de su estado metaestable anterior y da como resultado una ligera caída en la energía potencial. Estos pequeños ajustes de forma y energía terminan en 205 K, desde donde comienza la cuarta etapa y la superficie de la silla original se colapsa gradualmente en una partícula irregular con energía aún más minimizada.

Para examinar en detalle el mecanismo de deformación de la nanoplaca (001), investigamos los arreglos atómicos y la distribución de la tensión. Después de la relajación a 1 K, la energía potencial de la nanoplaca se libera en gran medida al doblar la estructura a lo largo de la dirección [110], como se discutió anteriormente. Durante la formación de este estado metaestable, no se observa difusión de átomos entre capas. La figura 2a presenta la vista vertical de su superficie superior. Tenga en cuenta que la situación en las otras dos capas atómicas se parece esencialmente a la que se describe a continuación. A partir del análisis de la estructura reticular, la mayoría de los átomos (excepto los coloreados en blanco) se identifican para formar (110) facetas, es decir, la rejilla inicial (001) se transforma en la estructura más compacta del cristal bcc y se produce la reconstrucción. . En la figura 2a, los átomos de las facetas adyacentes se asignan a diferentes colores. La celda unitaria de cada faceta está etiquetada por un rectángulo verde, en el que la línea amarilla corta indica su dirección [110] respectiva. Como puede verse, estas (110) facetas, que se ilustran esquemáticamente en la esquina inferior derecha de la figura 2a, están dispuestas en diferentes orientaciones. La distribución es aproximadamente simétrica. Tome una cuarta parte de la superficie total como ejemplo, las facetas 1 y 2 básicamente se alinean en paralelo, y son aproximadamente perpendiculares a las facetas 4 y 5. Los átomos en la faceta 3 están ligeramente distorsionados para acomodar las redes de ambas facetas 1 y 2.

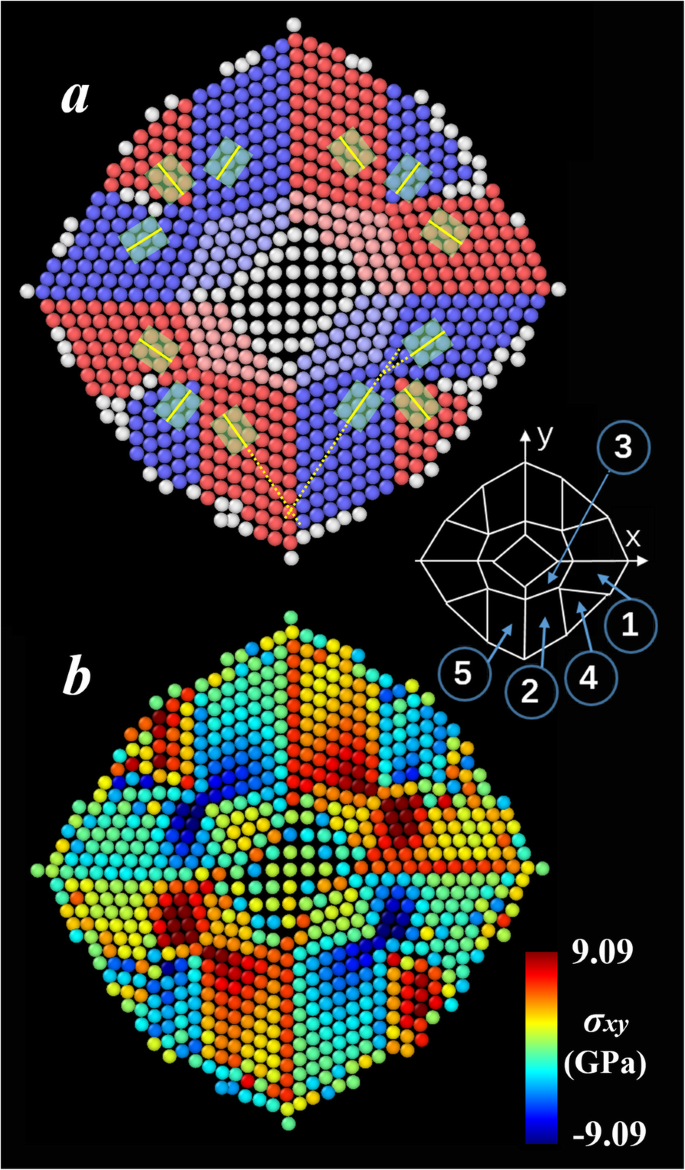
un Instantánea de la superficie superior de la nanoplaca (001) después de la relajación a 1 K y b la distribución del esfuerzo cortante correspondiente

A partir del análisis del esfuerzo calculado en la nanoplaca, se encuentra que el esfuerzo cortante muestra una aparente correlación con la deformación, lo que lo diferencia de otros componentes del tensor de esfuerzos. Por lo tanto, consideramos el esfuerzo cortante como la fuerza impulsada principal de la deformación por flexión y presentamos su distribución en la figura 2b. Claramente, la tensión ya no se distribuye uniformemente debido al orden de corto alcance inducido por la aparición de esas (110) facetas. De la comparación de la Fig. 2 ayb, se encuentra que la distribución de esfuerzos está altamente correlacionada con la disposición de orientación de las facetas. Las tensiones en las facetas rojas que se muestran en la Fig. 2a son generalmente positivas, mientras que son negativas en las azules. Esta observación sugiere que las facetas roja y azul tienden a moverse aproximadamente en direcciones opuestas. Se observa que existen espacios de tensión significativos cerca de los límites de los granos. Estas tensiones acumuladas van acompañadas de la formación de (110) facetas y se liberarían mediante una mayor deformación de la nanoplaca.

La Figura 3 muestra dos transformaciones críticas durante la posterior deformación de la nanoplaca (001). Para ser coherentes con la Fig. 2, solo ilustramos los átomos de la capa superior. Se presentan las distribuciones tanto de la tensión como de las coordenadas Z. Como se ve en la Fig. 3a, la distribución de la tensión en 8 K se asemeja a la situación en 1 K (ver Fig. 2b), y la flexión existe (ver Fig. 3c y Fig. 1d). Cuando la temperatura aumenta a 9 K, la flexión se desarrolla significativamente, como se ve en la Fig. 3d. Mientras tanto, uno puede encontrar que los espacios de tensión originalmente acumulados desaparecen (comparando la Fig. 3 ayb). La liberación del esfuerzo cortante es el resultado de esta deformación por flexión adicional. En consecuencia, la energía potencial disminuye (cf. Fig. 1) y la nanoplaca evoluciona a un estado más estable. En cuanto a la segunda transición que se muestra en la Fig. 3, comienza a 129 K y termina a 134 K, experimentando un rango de temperatura más amplio. Nótese que después de la transición que ocurre a 9 K, todavía existe una tensión positiva considerablemente grande en el área media de la superficie (ver Fig. 3b). En realidad, este estado de tensión se mantiene durante toda la segunda etapa del proceso de cambio de forma (9-129 K) (véase la figura 3e). Del mismo modo, también es la fuerza impulsora de la siguiente transición. Posteriormente, como se ve en la Fig. 3f, esos átomos rojos en la Fig. 3e se vuelven verdes (o azules), lo que indica que se libera la tensión positiva existente. Con el fin de resaltar la transformación de forma que ocurre entre 129 y 134 K, solo la mitad de los átomos en la superficie superior se exhiben en la Fig. 3 gyh, en la que el cuadro verde destaca el área cambiada. La región del cuadro verde se dobla hacia - Z dirección, lo que lleva a la desviación de la forma anterior del sillín. Esta desviación también podría ser confirmada por la caída obvia de R ² valor en la Fig. 1.

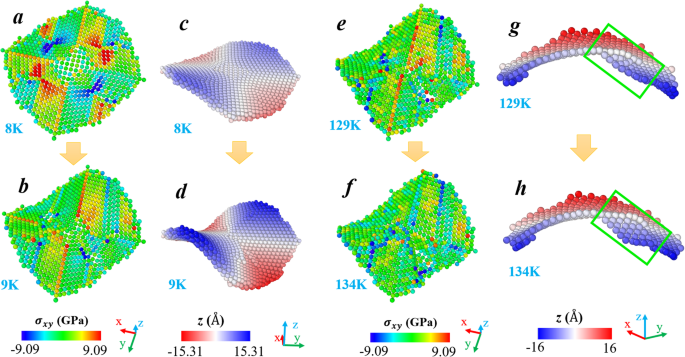
Dos transformaciones críticas durante la evolución de la temperatura de la nanoplaca (001). Para cada estado, los átomos se colorean respectivamente de acuerdo con a , b , e , f sus valores de esfuerzo cortante y c , d , g , h Z coordenadas

Como se discutió anteriormente, la transformación de forma de la nanoplaca (001) es impulsada por el esfuerzo cortante, cuya distribución depende en gran medida de la disposición de la red. Para ejemplificar aún más la posibilidad de adaptar la morfología a través del diseño de orientación cristalina, modelamos una nanoplaca de átomos de tres capas (110), en la que cada capa se divide en cuatro facetas orientadas diferentes, como se demuestra en la Fig. 4a (referida como "Nanoplaca modulada (110)" en adelante). Las líneas naranjas en la ilustración esquemática indican sus respectivas direcciones [110]. Para facilitar una comparación, mostramos la nanoplaca regular (110) en la Fig. 4d. Para la configuración inicial, la energía potencial calculada de la nanoplaca modulada (110) es igual a - 3.617 eV / átomo, mayor que el valor correspondiente de la nanoplaca regular (110) (- 3.668 eV / átomo) debido a la existencia de energía interfacial. En contraste con el patrón uniforme de distribución del esfuerzo cortante de la nanoplaca regular (110) (véase la Fig. 4e), aparecen notables espacios de esfuerzo entre las facetas adyacentes en la Fig. 4b. Estas brechas son especialmente significativas entre los átomos ubicados cerca de los límites de los granos. Después de la relajación a 1 K, la región con gradiente de tensión se extiende para involucrar más átomos alrededor de los límites, como se ve en la figura 4c. Mientras tanto, la energía potencial promedio cae a - 3.653 eV / átomo, y la configuración de flexión da como resultado una placa de asiento, similar a la nanoplaca (001). Como la temperatura se eleva continuamente, durante la evolución de la forma de la nanoplaca modulada (110), se pueden identificar tres etapas con 179 y 277 K como puntos críticos. En la primera etapa, la forma del sillín básicamente se mantiene a pesar de fluctuaciones menores, como se ejemplifica en la instantánea insertada de 100 K. Sin embargo, después de la transición que ocurre a 179 K, la configuración vuelve a convertirse en un disco y mantiene esta forma sin cambios obvios. a lo largo de la segunda etapa (ver, por ejemplo, la instantánea insertada de 200 K). Alrededor del punto crítico (179 K), observe que la parte elevada en el centro combinada con el plano de la superficie fragmentada todavía corresponde a la configuración con menor energía. Finalmente, cuando la temperatura alcanza los 277 K, el sistema comienza a contraerse a partículas irregulares (cf. la instantánea insertada de 300 K), lo que lleva a la reducción radical de la energía potencial, similar a la cuarta etapa de la nanoplaca (001) descrita. más temprano. Tenga en cuenta que la energía potencial de la nanoplaca regular (110) comienza a disminuir drásticamente a 552 K (los puntos de datos correspondientes no se presentan por completo en la Fig.1), la nanoplaca modulada (001) muestra una estabilidad de forma significativamente disminuida. Estos resultados indican que el diseño de orientaciones cristalinas es un enfoque eficiente para modular la estabilidad de la forma.

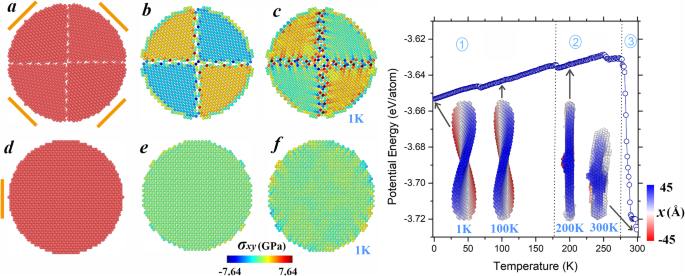
Panel izquierdo:ilustración esquemática de a la nanoplaca modulada (110) y d el regular. b , c , e , f Muestre respectivamente sus distribuciones de esfuerzos cortantes en las configuraciones iniciales y a 1 K. Panel derecho:energías potenciales dependientes de la temperatura de la nanoplaca modulada (110). Las instantáneas en las inserciones se toman a temperaturas representativas

Para obtener una comprensión completa de los patrones de evolución de la forma, consideramos nanoplacas bcc Fe (001) con diferentes diámetros (incluido d =12 a , 40 a y 50 a ). Sus energías potenciales y configuraciones típicas durante el proceso de calentamiento se muestran en la Fig. 5. Tenga en cuenta que la nanoplaca antes mencionada con d =32 a también se muestra a modo de comparación. Con una energía potencial relativamente alta, la nanoplaca más pequeña experimenta más etapas en comparación con las demás. Como se ve en la instantánea de la Fig. 5a, la nanoplaca con un diámetro de 12 a mantiene sus superficies planas (a) hasta que la flexión comienza a ocurrir a 52 K (b) y finalmente se forma la forma de silla de montar a 62 K (c). Sin embargo, esta estructura de silla no dura en un amplio rango de temperatura, y la siguiente difusión entre capas ocurre a 84 K, lo que lleva a una fuerte disminución de la energía potencial. La nanoplaca engrosada, ejemplificada en la Fig. 5 (d), mantiene su característica hasta que aparece una concentración adicional a aproximadamente 200 K. En cuanto a la nanoplaca con d =40 a , la forma de la silla de montar se mantiene estable a temperaturas que oscilan entre 1 y 190 K antes de colapsar en una partícula compacta. En el caso de la nanoplaca con d =50 a , la forma del sillín permanece hasta 134 K (indicada por la flecha en el punto “g”) y luego se distorsiona a una estructura irregular, como se ilustra en la Fig. 5f. Como puede verse, a 190 K, donde la nanoplaca con d =40 a comienza a colapsar, el que tiene d =50 a ya ha completado su transformación de forma de silla de montar a irregular. Estas observaciones sugieren que, a medida que el diámetro aumenta de 12 a a 40 a , el rango de temperatura donde la forma del sillín podría ser estable se amplía gradualmente; sin embargo, cuando el diámetro sigue creciendo (a 50 a , por ejemplo), la estabilidad de la forma del sillín disminuye hasta cierto punto. Es decir, aunque un diámetro mayor conduce a una mejor estabilidad estructural (menor energía potencial en el estado fundamental), no es el único factor determinante que afecta la estabilidad, la influencia de otros aspectos (como los efectos cinéticos y de entropía) también juega un papel importante. especialmente cuando la nanoplaca es lo suficientemente grande.

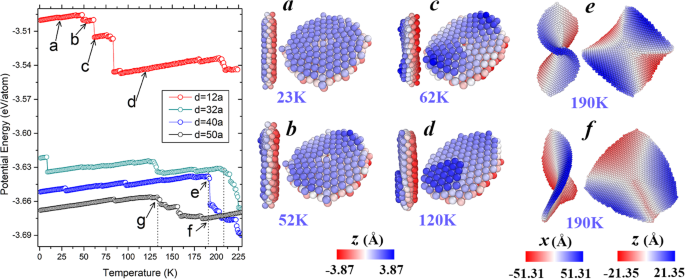
Panel izquierdo:Evoluciones de temperatura de energías potenciales de nanoplacas bcc Fe (001) con diferentes diámetros. Panel derecho:instantáneas de la nanoplaca con d =12 a en a 23 K, b 52 K, c 62 K y d 120 K; Instantáneas de la nanoplaca con e d =40 a a 190 K y (f) d =50 a a 190 K

Además del efecto del diámetro, también se consideran nanoplacas con diferentes espesores. La energía potencial de la nanoplaca ( d =32 a ) con diferentes capas se muestran en la Fig. 6. Tenga en cuenta que la nanoplaca de 3 capas atómicas antes mencionada también se muestra a modo de comparación. Como se ve a partir de la evolución de las energías potenciales, se encuentra que las nanoplacas con 1 o 2 capas atómicas experimentan obviamente más etapas en comparación con la de 3 capas. En realidad, colapsan a formas irregulares a temperaturas mucho más bajas. Por el contrario, la estructura original de la nanoplaca con 4 capas se mantiene bien hasta 97 K (cf. Fig. 6a). Sin embargo, a 98 K, sus planos en forma de disco (001) se transforman en planos elípticos (110) con mayor estabilidad (ver Fig. 1), lo que se acompaña de una abrupta disminución de la energía potencial. Esta nanoplaca de 4 capas (110) generada conserva su configuración hasta que se produce la fusión. Estos resultados muestran que las nanoplacas más gruesas generalmente presentan una mejor estabilidad y la forma de silla solo existe en espesores relativamente pequeños. Para obtener más información sobre la generalidad de los patrones de evolución, también modelamos varias otras nanoplacas metálicas bcc (incluidas W, Nb, Mo y Cr) con diámetros de 32 a , que consta de tres capas de átomos orientados (001) inicialmente. La Figura 7 ilustra las energías potenciales dependientes de la temperatura de estas nanoplacas y las instantáneas atomísticas asociadas a temperaturas representativas. Después de la relajación a 1 K, todos los planos originalmente uniformes (001) reconstruyen y forman (110) facetas con diferentes orientaciones. A temperaturas más bajas, la forma de la silla, como un estado metaestable universal, aparece en cada nanoplaca, similar al caso de la nanoplaca de Fe. Con el avance del calentamiento, la transformación en una partícula irregular ocurre a diferentes temperaturas, donde las energías potenciales disminuyen drásticamente. Comparativamente, la etapa de forma de silla para nanoplacas W dura en el rango de temperatura más amplio (hasta 582 K), lo que se atribuye a su extraordinaria estabilidad estructural (inicial E _p =- 7,94 eV / átomo). Por el contrario, la nanoplaca de Cr menos estable mantiene su forma de silla de montar solo hasta 62 K, después de lo cual aparecen los golpes y pandeo sucesivamente (véanse las instantáneas tomadas a 61 y 250 K en la Fig. 7). En cuanto a las otras dos nanoplacas, Nb tiende a restaurar la superficie plana original (cf. la instantánea de 135 K en la Fig. 7), y Mo presenta una flexión significativa (cf. la instantánea de 150 K) antes de su colapso final. Estas dos situaciones se parecen aproximadamente a las nanoplacas de Fe moduladas (110) y (001). Los resultados anteriores muestran que los estados metaestables observados en las nanoplacas de Fe también existen en otras nanoplacas metálicas bcc. Las configuraciones con diferente estabilidad estructural siguen diferentes patrones de evolución. Además, se observa que en la mayoría de nuestras simulaciones, las nanoplacas se transforman en partículas compactas incluso por debajo de la temperatura ambiente, lo cual es resultado de sus pequeños tamaños. Aún así, los mecanismos de evolución identificados son de importancia general. Los resultados de la estabilidad relativa de estas nanoplacas entre diferentes orientaciones de planos, tamaños y elementos podrían extrapolarse a sistemas más grandes. La descripción de los mecanismos de transformación de la forma puede servir como referencia para obtener las morfologías deseadas mediante el control o la aleación de la orientación cristalina [31, 32].

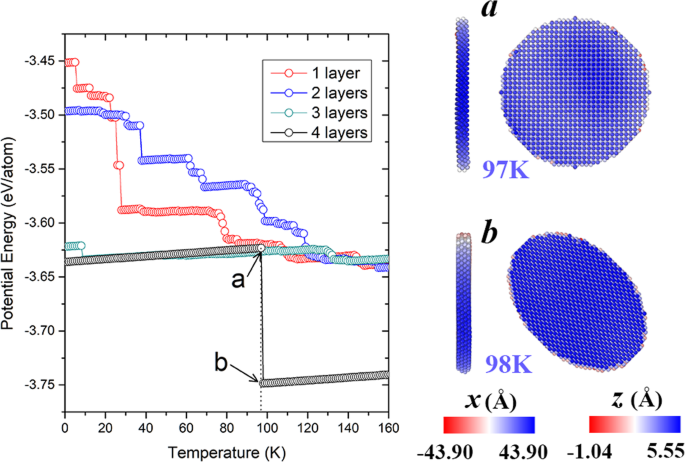
Panel izquierdo:Evoluciones de temperatura de energías potenciales de nanoplacas de Fe (001) con diferente número de capas. Panel derecho:instantáneas de la nanoplaca con 4 capas respectivamente en a 97 K y b 98 K

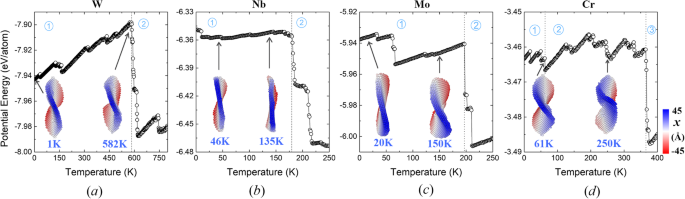
Evoluciones de temperatura de energías potenciales de a W, b Nb, c Mo y d Nanoplacas de Cr respectivamente. Las instantáneas de los estados representativos se muestran como recuadros

Conclusiones

En resumen, la evolución de la forma de las nanoplacas bcc Fe con superficies de índice bajo se investigó mediante simulaciones de MD. La discrepancia en la estabilidad estructural conduce a diversos patrones en las transformaciones morfológicas. (110) nanoplate es el más estable y mantiene su configuración inicial hasta la temperatura más alta. Por el contrario, las nanoplacas (111) y (001) no pueden existir firmemente, ambas tienden a colapsar en partículas irregulares incluso por debajo de la temperatura ambiente. Sin embargo, antes de este colapso final, la superficie de la nanoplaca (001) se convierte en (110) facetas con diferentes orientaciones y, mientras tanto, forma una forma de silla de montar, que se mantiene en un rango de temperatura relativamente amplio. Este proceso de transformación es impulsado por el esfuerzo cortante, cuya distribución está estrechamente asociada con la disposición de las facetas. Una mayor flexión y pandeo durante el calentamiento posterior corresponden a la liberación de tensión. Además, se realizaron simulaciones en la nanoplaca modulada (110), nanoplacas (001) de diferentes diámetros y espesores, y otras nanoplacas metálicas bcc (001). Los resultados muestran que la evolución de la forma se puede ajustar mediante las orientaciones de las facetas, los tamaños de las placas y los componentes. Este estudio revela el mecanismo a nivel atómico de la evolución de la forma de las nanoplacas metálicas bcc y, por lo tanto, proporciona una base teórica sobre el control de la morfología en la síntesis de nanomateriales metálicos.

Disponibilidad de datos y materiales

Todos los datos generados o analizados durante este estudio se incluyen en este artículo publicado.

Abreviaturas

a:

Constante de celosía

bcc:

Cuerpo centrado-cúbico

d:

diámetro

EAM:

Método de átomo incrustado

E _p :

Energía potencial

MD:

Dinámica molecular

R ² :

Coeficiente de determinación

TEM:

Microscopio electrónico de transmisión

Primer estudio de principios de penta-siligrafeno como material anódico de alto rendimiento para baterías de iones de litio Caracterizaciones espectroscópicas Raman de nanoestructuras unidimensionales de InP / InAs / InP autocatalizadas en un sustrato de InP (111) B utilizando un método simple de inclinación del sustrat…