Efecto de la deformación en el rendimiento termoeléctrico de la monocapa InSe

Resultado y discusión

Monocapa InSe es una hoja atómica cuádruple con Se-In-In-Se que se une covalentemente en una capa. Desde una vista superior, la monocapa presenta una red en forma de panal, y cada átomo de Se está enlazado con otros tres átomos de In, como se muestra en la Fig. 1a. Sobre la base de la minimización de la energía total, los parámetros de la red de este cristal se calculan para ser a ₀ =3,95 Å. En este artículo, empleamos la deformación biaxial en la monocapa InSe manteniendo la simetría cristalina cambiando sus redes como δ =( a - a ₀ ) / a ₀ × 100%, donde a y a ₀ son la constante de celosía de la monocapa InSe con deformación y sin deformación, respectivamente. Cuando se impone la deformación por tracción biaxial sobre la monocapa InSe, la longitud de enlace d _InSe aumenta monótonamente con el aumento de la deformación, y esto conduce al aumento del ángulo de unión de In-Se-In (ver Fig. 1b).

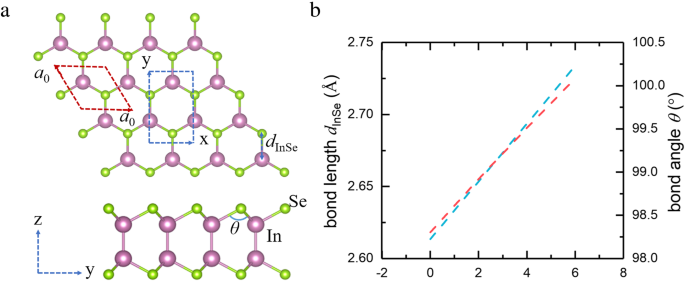
un Vista superior y lateral del InSe monocapa. Las bolas rosadas y verdes representan átomos de In y Se, respectivamente. b La variación de la longitud de enlace y el ángulo de enlace con el aumento de la deformación por tracción biaxial. El a básico ₀ × a ₀ celda unitaria y x × años Las supercélulas de la monocapa InSe se indican con líneas discontinuas rojas y azules, respectivamente

La monocapa InSe exhibe un semiconductor indirecto con la banda prohibida de 1.67 eV, donde el mínimo de la banda de conducción (CBM) existe en el punto Г, y los sitios de la banda de valencia máxima (VBM) entre los puntos Г y K, como se muestra en la Fig. 2a. La banda de valencia de la monocapa de InSe exhibe una dispersión de sombrero mexicano, que también se puede encontrar en muchos materiales bidimensionales [36,37,38,39]. La modificación de la estructura de la banda en respuesta a la deformación por tracción se investigó en la Fig. 2, y los tres extremos de la banda de conducción se indican con los símbolos I, II y III, respectivamente. Bajo una deformación por tracción, la banda de conducción de menor energía es sensible a la deformación y se desplaza hacia abajo, mientras que la banda de valencia permanece casi constante, dando lugar a la reducción de la banda prohibida. Sin tensión, existen pequeñas diferencias entre el mínimo de la segunda y la tercera banda de conducción, y los valles de la banda tienden a converger. Sin embargo, con el aumento de la deformación por tracción, la diferencia de energía aumenta gradualmente. También comparamos las bandas prohibidas en diferentes cepas con resultados teóricos y experimentales relacionados, como se detalla en el archivo adicional 1:Tabla S2.

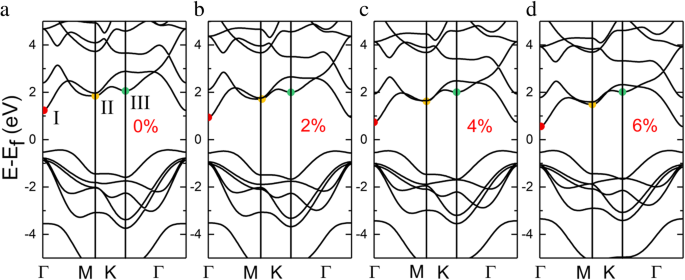
Estructura de la banda de la monocapa InSe en diferentes condiciones de deformación

Efecto de la deformación por tracción en los coeficientes de transporte termoeléctrico

Sobre la base de la estructura electrónica calculada, realizamos cálculos del coeficiente de transporte termoeléctrico mediante la teoría semiclásica de Boltzmann. Con respecto al tiempo de dispersión τ , Coeficiente de Seebeck S y conductividad eléctrica σ se puede calcular. La Figura 3a muestra el coeficiente de Seebeck calculado en función del nivel de Fermi. Por simplicidad, a menudo se supone que la estructura de la banda permanece sin cambios desde el dopaje a temperaturas finitas [40, 41], y el efecto de dopaje sobre el coeficiente de transporte termoeléctrico puede obtenerse mediante la variación de la posición del nivel de Fermi. Un ε negativo _f indica el dopaje de tipo p moviendo el nivel de Fermi a la banda de valencia, y se puede obtener el coeficiente de Seebeck positivo. De manera similar, un ε positivo _f dio un coeficiente de Seebeck negativo. Podemos encontrar que el resultado obtenido sin deformación está muy cerca del informe anterior [17], y el máximo del coeficiente de Seebeck disminuye con el aumento de la deformación por tracción, lo que está relacionado con el cambio de la banda prohibida [42].

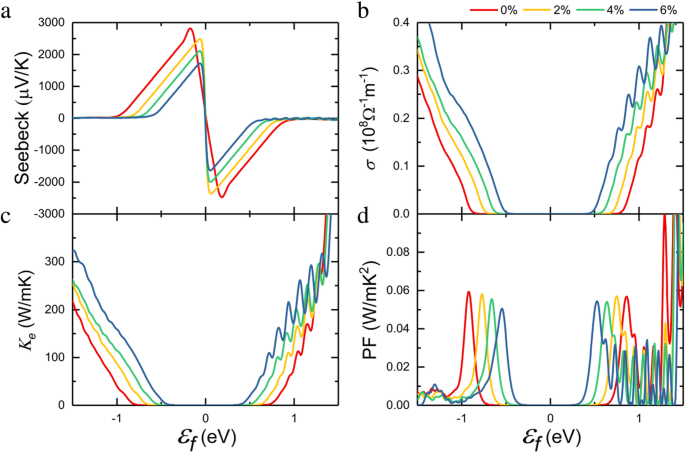
un Coeficiente de Seebeck, b conductividad eléctrica, c conductividad térmica electrónica, d factor de potencia de la monocapa InSe en función del potencial químico a 300 K cuando se aplica la diferente deformación biaxial

Para calcular la conductividad eléctrica σ , tiempo de relajación τ es necesario porque la salida es σ / τ en código BoltzTraP. En este documento, τ está determinado por

donde μ es la movilidad del portador y m * es la masa efectiva. En la teoría del potencial de deformación, la movilidad del portador en materiales 2D se puede calcular mediante [43, 44]

Aquí, e es la carga del electrón, ℏ es la constante de Planck y k _B es la constante de Boltzmann. C representa el módulo de elasticidad y se puede calcular con C =( ∂ ² E / ∂δ ² ) / S ₀ , donde E , δ y S ₀ son la energía total, la deformación aplicada y el área en equilibrio para el sistema 2D, respectivamente. E ₁ es la constante de potencial de deformación mostrada como E ₁ = ΔE _borde / Δδ , donde ΔE _borde es el cambio de energía de los bordes de la banda. m _d es la masa efectiva promedio derivada de \ ({m} _d =\ sqrt {m_x ^ {\ ast} {m} _y ^ {\ ast}} \). Para calcular la movilidad, una x rectangular × años La supercélula se adopta como se muestra en la Fig. 1a. El valor obtenido de C a lo largo de x ( y ) dirección es 60,43 N / m (53,68 N / m), que se obtiene ajustando la curva de la relación energía-deformación, como se muestra en el archivo adicional 1:Figura S1. El potencial de deformación calculado E ₁ es 6.13 eV (6.14 eV) para el electrón a lo largo de x ( y ) dirección, y 3,45 eV (3,33 eV) para el orificio a lo largo de x ( y ) dirección. Los resultados calculados de masa efectiva, movilidad del portador y tiempo de relajación para la monocapa InSe bajo diferentes deformaciones se resumen en la Tabla 1. Podemos encontrar esa pequeña diferencia junto con diferentes direcciones, y la masa y movilidad efectivas del portador es isotrópica general. Por lo tanto, usamos el valor promedio de x y y instrucciones para evaluar posteriormente el rendimiento termoeléctrico. Las masas efectivas de los huecos se mejoran con la deformación aplicada, mientras que las masas efectivas para los electrones permanecen casi sin cambios. Con el tiempo de relajación calculado, se puede obtener la conductividad eléctrica a un potencial químico dado en la Fig. 3b. Puede verse que la conductividad eléctrica σ aumenta con el aumento de la deformación por tracción en un sistema dopado de tipo p pesado debido a la mejora de la movilidad del orificio, mientras que σ sigue siendo relativamente bajo con un nivel de dopaje bajo. Además, la tendencia de la conductividad térmica electrónica se mantiene con la conductividad eléctrica a través de la ley de Wiedemann-Franz: K _e = LσT en la Fig. 3c, donde L es el número de Lorenz. El factor de potencia se puede obtener mediante PF = S ² σ / τ , que determina cuánta electricidad se puede generar. Teniendo en cuenta la tendencia general del coeficiente de Seebeck y la conductividad eléctrica, la deformación por tracción reduce ligeramente el factor de potencia, como se observa en la Fig. 3d.

Efecto de la deformación por tracción en Κ _l

En los metales, los electrones son los responsables de los portadores de calor, mientras que en los semiconductores y los sólidos dieléctricos donde el dopaje y la temperatura no son muy elevados, las vibraciones reticulares serán el principal motivo del transporte de energía [45]. La conductividad térmica de celosía es un parámetro muy importante para la aplicación termoeléctrica. Desde el punto de vista teórico y como una simple aproximación, la conductividad térmica de la celosía Κ _l se puede expresar de la siguiente manera [46,47,48]:

donde C _λ , v _λ y V son la contribución de calor específica, la velocidad del grupo de fonones y el volumen del cristal, respectivamente. τ _λ es el tiempo de relajación del modo λ, que se puede estimar utilizando la regla de Matthiessen [49]:

donde \ (\ frac {1} {\ tau _ {\ uplambda} ^ b} \) es la tasa de dispersión del límite, \ (\ frac {1} {\ tau _ {\ uplambda} ^ {\ mathrm {iso}}} \ ) es la tasa de dispersión de impurezas isotrópicas, y \ (\ kern0.1em \ frac {1} {\ tau _ {\ uplambda} ^ {3 \ mathrm {ph}}} \) es la tasa de dispersión de tres fonones.

La Figura 4a presenta Κ _l variación de la monocapa InSe con temperatura bajo diferente tensión. La conductividad térmica de la red en el caso libre de deformaciones es de 25,9 W / mK a temperatura ambiente, lo que es comparable con el informe anterior [19]. Cuando la deformación aplicada aumenta al 6%, la conductividad térmica de la red se reduce a 13,1 W / mK, lo que confirma que la ingeniería de deformaciones es un método muy eficaz para modificar la conductividad térmica de la red. Trazamos la correspondiente curva de dispersión de fonones de la monocapa de InSe para diferentes cepas en la Fig. 4c, para determinar el origen de la reducción en la conductividad térmica de la red. Contiene 12 modos de fonón, ya que la monocapa InSe tiene una celda unitaria de cuatro átomos. No hay frecuencia negativa en los espectros de fonones, lo que confirma que la monocapa de InSe es térmicamente estable. Tres ramas que comienzan desde 0 en la región de baja energía de la curva de dispersión de fonones son z -eje acústico (ZA), longitudinal acústico (LA) y transversal acústico (TA), respectivamente, y los demás son modos ópticos. Con el aumento de la deformación por tracción, la naturaleza cuadrática del modo ZA cambia a casi una línea recta en la región de baja energía. La tendencia a la baja en la frecuencia de los modos ópticos se puede observar bajo tensión de tracción, porque la tensión de tracción debilita los enlaces y luego conduce a frecuencias más bajas. También discutimos la contribución de cada rama de phonon hacia Κ _l para la monocapa InSe sin tensar y con cepa al 6% en la Fig. 4b. Para la condición libre de deformación, el modo ZA contribuye significativamente a transportar calor, y cuando se aplica un 6% de deformación por tracción a la monocapa InSe, la contribución relativa del modo ZA disminuye del 58 al 38%. A medida que aumenta la deformación por tracción, el modo ZA se vuelve más difícil, lo que conduce a una menor contribución a Κ _l .

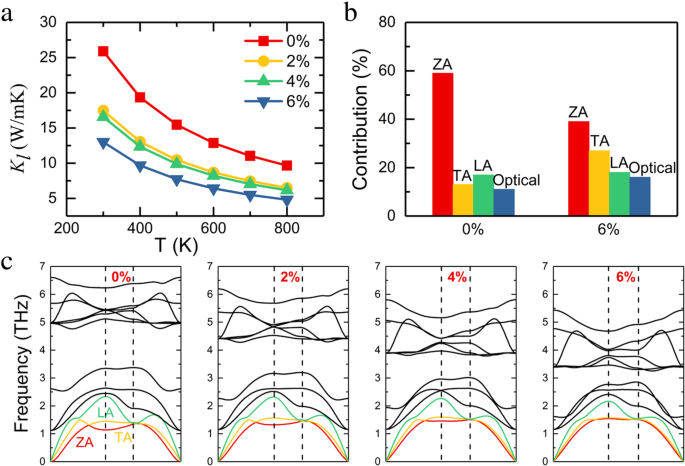
un Efectos de la deformación biaxial calculada sobre la conductividad térmica de la red a diferentes temperaturas. b Contribución de ZA, TA, LA y todas las ramas ópticas hacia la conductividad térmica de la red para sistemas no tensados ​​y al 6% tensos. c Las curvas de dispersión de fonones de la monocapa InSe para diferentes cepas

A continuación, se presenta un análisis detallado de la variación de la velocidad del grupo de fonones inducida por la deformación por tracción para comprender las propiedades de transporte de fonones. Para los modos acústicos en el plano, las velocidades de los grupos de fonones se reducen a una deformación del 6%, como se muestra en la Fig. 5a, b. Combinado con la contribución mejorada de LA y TA, la disminución de la velocidad del grupo de fonones juega un papel vital en la reducción de Κ _l . El cambio de las velocidades de los grupos de fonones se origina a partir de la variación de la estructura inducida por la deformación:cuando se activa la deformación por tracción, la distancia de unión aumenta y la fuerza de unión disminuye, lo que conduce a una frecuencia de fonones y una velocidad de grupo más bajas. Teniendo en cuenta que tres ramas de fonones acústicos contribuyen principalmente a Κ _l , el aumento de la velocidad del grupo de fonones de las ramas ópticas tiene un efecto limitado.

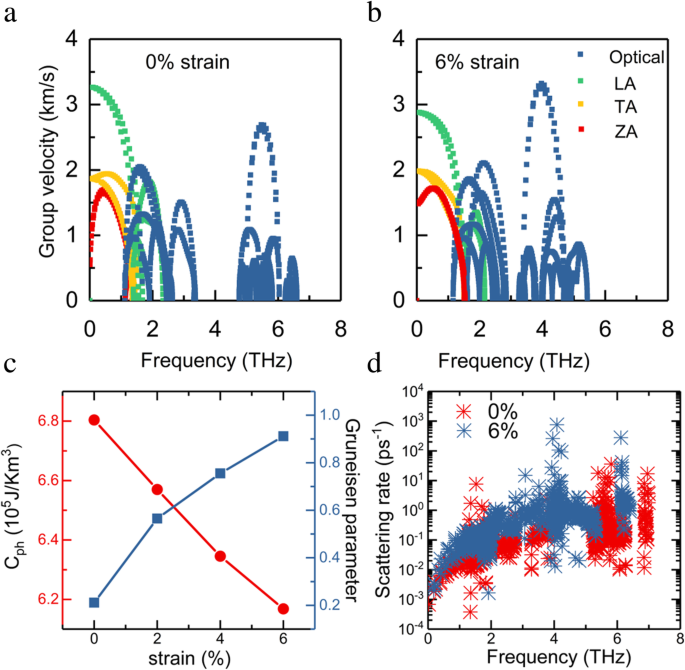
La contribución de los modos ZA, TA, LA y ópticos a la velocidad de grupo de InSe monocapa para ( a ) sin tensión y ( b ) 6% de sistemas tensos. c Capacidad calorífica del fonón ( C _ph ) y el parámetro de Gruneisen en función de la deformación a 300 K. d Tasa de dispersión de fonones de InSe monocapa no tensada y tensada al 6% en función de la frecuencia.

La tasa de dispersión de tres fonones de la monocapa InSe sin y con una deformación del 6% en función de la frecuencia se representa en la Fig. 5d. Puede observarse que la tasa de dispersión de tres fonones del 6% de InSe de monocapa tensada en la región de frecuencia más baja es significativamente mayor que la del caso sin tensar, lo que indica que el aumento de tensión da lugar a una dispersión de tres fonones más fuerte. La dispersión mejorada de tres fonones es principalmente responsable de la conductividad térmica de la red reducida, que también es consistente con la conclusión anterior [19]. En ZrS ₂ se ha observado una tendencia similar de la tasa de dispersión de fonones con el aumento de la deformación por tracción. y 2H MoTe ₂ monocapa [50, 51]. También analizamos el efecto de la deformación por tracción biaxial sobre la capacidad calorífica del fonón ( C _ph ), como se presenta en la Fig. 5c. Con el aumento de la deformación por tracción, la capacidad calorífica del fonón de la monocapa de InSe disminuye monótonamente. Para el sistema con un 6% de tensión, la capacidad calorífica del fonón se reduce a 6,2 × 10 ⁵ J / Km ³ . Debido a la linealización y rigidez del modo ZA, la densidad de estados de fonones disminuye, lo que conduce a una capacidad calorífica de fonones reducida. Los parámetros de Gruneisen proporcionan información sobre la anarmonicidad de un sistema y pueden obtenerse de las constantes de fuerza interatómicas anarmónicas (IFC) [32, 52]. La Figura 5c muestra los parámetros de Gruneisen calculados bajo diferentes cepas. El aumento del parámetro de Gruneisen inducido por la deformación por tracción significa una anarmonicidad más fuerte, lo que conduce a una conductividad térmica más baja [18].

Con todas las propiedades de transporte termoeléctrico disponibles, se puede obtener la figura de mérito, ZT. La deformación por tracción aplicada tiene un efecto diferente sobre estas propiedades de transporte, y la mejora del rendimiento termoeléctrico de la monocapa de InSe requiere un equilibrio complicado entre estos parámetros S , σ y κ . La Figura 6 muestra la cifra calculada de mérito con diferente cepa en función del potencial químico a 300 K, y es obvio que la variación del valor de ZT bajo diferentes cepas depende en gran medida del potencial químico y el valor máximo de ZT se puede mejorar de manera efectiva con el aumento de la tensión. Sin tensión, la monocapa de InSe tiene un valor de ZT pico de 0,36 a temperatura ambiente, que es cercano al de silicene (0,36), germanene (0,41) y MoS de una sola capa ₂ (0,58) [53, 54], y menor que el de los monocalcogenuros 2D (1,29 ~ 2,63 a 700 K) [55]. Teniendo en cuenta la alta movilidad del portador y la flexibilidad mecánica superior, la monocapa de InSe tensa también es un material potencial prometedor para la aplicación termoeléctrica. Cuando se aplica tensión de tracción, el enlace interatómico debilitado induce una anarmonicidad más fuerte. El aumento de la tasa de dispersión de fonones, la disminución de la velocidad del grupo de fonones y la capacidad calorífica de los fonones juntos dieron como resultado una conductividad térmica de celosía reducida, lo que condujo a una figura de mérito mejorada. Cálculos teóricos anteriores demostraron que la monocapa de InSe puede soportar una deformación por tracción superior al 20%, que es mucho mayor que nuestras deformaciones previstas [20]. En el experimento, la aplicación de una deformación en materiales 2D se debe principalmente a su interacción con los sustratos, que puede ser inducida por el calentamiento [56], el desajuste de celosía entre películas delgadas epitaxiales [57] o la flexión del material 2D sobre el sustrato [58, 59]. En realidad, es experimentalmente más común aplicar tensión uniaxial en lugar de tensión biaxial. Según los informes anteriores [20], una cepa uniaxial puede mostrar una mejora similar en las propiedades termoeléctricas de la monocapa InSe.

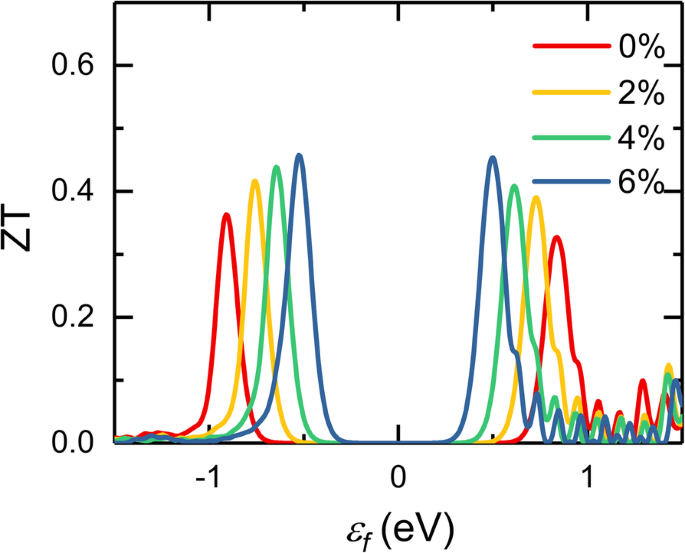
Cifra de mérito calculada de la monocapa InSe en función del potencial químico bajo diferentes tensiones

Conclusión

En conclusión, investigamos sistemáticamente el posible impacto de la deformación por tracción biaxial en las propiedades de transporte electrónico, termoeléctrico y de fonones para la monocapa de InSe mediante cálculos de primeros principios. La banda prohibida disminuye a medida que aumenta la deformación por tracción, lo que conduce a la reducción del coeficiente de Seebeck. La deformación por tracción también indujo una dispersión anarmonica más fuerte, y la reducción de la conductividad térmica de la red podría atribuirse al aumento resultante de la tasa de dispersión de fonones, la disminución de la velocidad del grupo de fonones y la capacidad calorífica de fonones. La reducción de la conductividad térmica de la celosía supera a la del coeficiente de Seebeck, lo que produce un rendimiento mejorado con el aumento de la deformación por tracción.

Disponibilidad de datos y materiales

Los conjuntos de datos generados y / o analizados durante el estudio actual están disponibles a pedido del autor correspondiente.

Abreviaturas

2D:

Dos dimensiones

CBM:

Banda de conducción mínima

τ :

Tiempo de relajación

C _ph :

Capacidad calorífica de Phonon

FET:

Transistor de efecto de campo

LA:

Dispersión longitudinal de fonones acústicos

PF:

Factor de potencia

S :

Coeficiente de Seebeck

TA:

Dispersión transversal de fonones acústicos

VBM:

Máximo de banda de valencia

ZA:

z -Eje de dispersión de fonones acústicos

ZT:

Figura de mérito

ε _f :

Nivel Fermi

Κ _e :

La conductividad térmica con las contribuciones de los portadores electrónicos

Κ _l :

La conductividad térmica con las contribuciones de la red

σ :

Conductividad eléctrica

Dependencia de las propiedades electrónicas y ópticas de las multicapas MoS2 en el acoplamiento entre capas y la singularidad de Van Hove Ruedas de vagón c-Si y c-SiGe reducidas para la visualización de la anisotropía y la selectividad de los agentes decapantes químicos húmedos