Notación de suma y producto

Como referencia, esta sección presenta la terminología utilizada en algunos textos para describir los términos mínimos y máximos asignados a un mapa de Karnaugh. De lo contrario, no hay material nuevo aquí.

Terminología para términos mínimos

Σ (sigma) indica suma y "m" minúscula indica minitérminos. Σm indica la suma de minitérminos. El siguiente ejemplo se revisa para ilustrar nuestro punto. En lugar de una descripción de ecuación booleana de lógica no simplificada, enumeramos los términos mínimos.

 f (A, B, C, D) =Σ m (1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15) o f (A, B, C, D) =Σ (m  1  , m  2  , m  3  , m  4  , m  5  , m  7  , m  8  , m  9  , m  11  , m  12  , m  13  , m  15  ) 

Los números indican la ubicación de la celda, o la dirección, dentro de un mapa de Karnaugh, como se muestra a continuación a la derecha. Este es ciertamente un medio compacto de describir una lista de minitérminos o celdas en un mapa K.

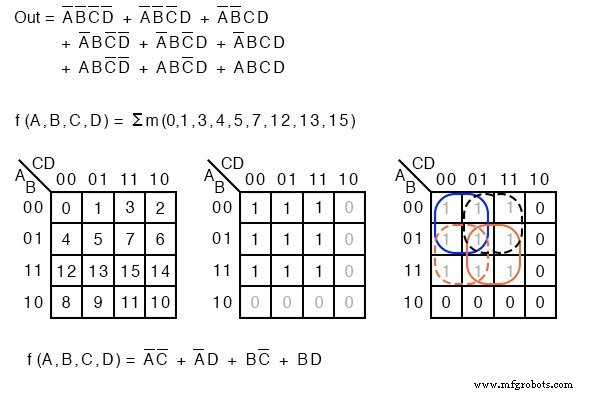
La solución Sum-Of-Products no se ve afectada por la nueva terminología. Los minitérminos, 1 s, en el mapa se han agrupado como de costumbre y se ha escrito una solución de suma de productos.

Terminología para Maxterms

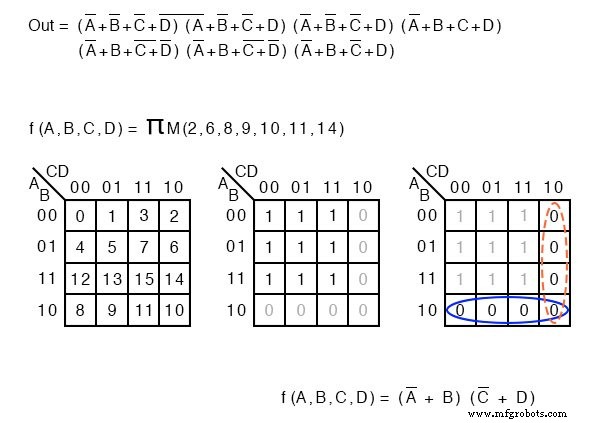
A continuación, mostramos la terminología para describir una lista de términos máximos. El producto se indica con el griego Π (pi) y la “M” mayúscula indica términos máximos. ΠM indica producto de maxterms. El mismo ejemplo ilustra nuestro punto.

La descripción de la ecuación booleana de lógica no simplificada se reemplaza por una lista de términos máximos.

 f (A, B, C, D) =Π M (2, 6, 8, 9, 10, 11, 14) o f (A, B, C, D) =Π (M  2  , M  6  , M  8  , M  9  , M  10  , M  11  , M  14  ) 

Una vez más, los números indican las ubicaciones de las direcciones de las celdas de K-map. Para maxterms, esta es la ubicación de 0 s, como se muestra a continuación. Una solución Producto-DE-Sumas se completa de la manera habitual.

$$ Fuera =(A + B + \ bar {C} + D) (A + \ bar {B} + \ bar {C} + D) + (\ bar {A} + B + C + \ bar {D }) + (\ bar {A} + B + \ bar {C} + D) $$

$$ (\ bar {A} + B + \ bar {C} + \ bar {D}) (\ bar {A} + \ bar {B} + \ bar {C} + D) $$

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de expresiones de suma de productos y producto de sumas
• Hoja de trabajo de mapeo de Karnaugh
• Hoja de trabajo de álgebra booleana