Forma polar y notación de forma rectangular para números complejos

Para trabajar con números complejos sin dibujar vectores, primero necesitamos algún tipo de notación matemática estándar. Hay dos formas básicas de notación de números complejos: polar y rectangular .

Forma polar de un número complejo

La forma polar es donde un número complejo se denota por la longitud (también conocido como magnitud , valor absoluto o módulo ) y el ángulo de su vector (generalmente denotado por un símbolo de ángulo que se ve así:∠).

Para usar la analogía del mapa, la notación polar para el vector de la ciudad de Nueva York a San Diego sería algo así como "2400 millas, suroeste". Aquí hay dos ejemplos de vectores y sus notaciones polares:

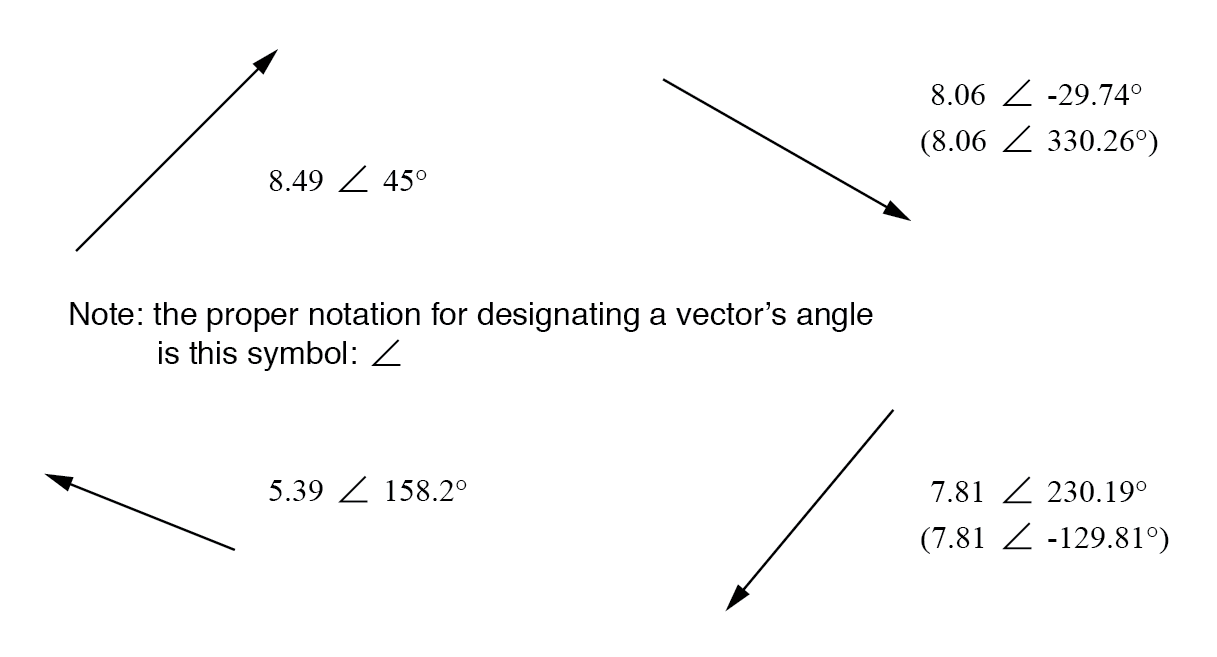
Vectores con notaciones polares.

La orientación estándar para los ángulos vectoriales en los cálculos de circuitos de CA define 0 ° como a la derecha (horizontal), haciendo 90 ° hacia arriba, 180 ° hacia la izquierda y 270 ° hacia abajo. Tenga en cuenta que los vectores en ángulo "hacia abajo" pueden tener ángulos representados en forma polar como números positivos superiores a 180 o números negativos inferiores a 180.

Por ejemplo, también se puede decir que un vector con un ángulo de ∠ 270 ° (hacia abajo) tiene un ángulo de -90 °. (Figura siguiente) El vector de arriba a la derecha (7.81 ∠ 230.19 °) también se puede denotar como 7.81 ∠ -129.81 °.

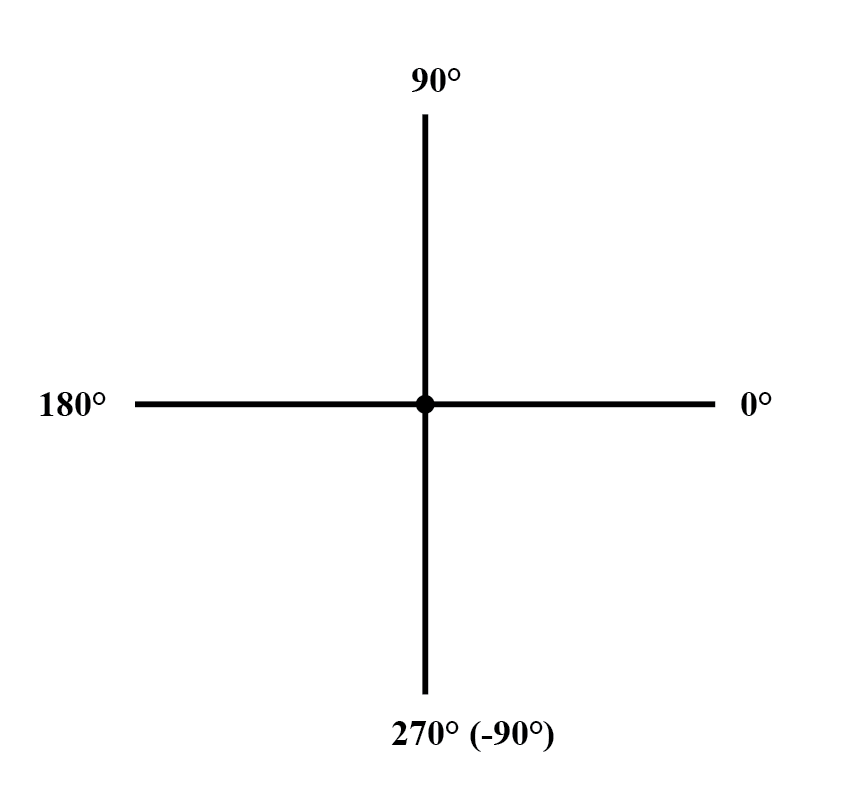
La brújula vectorial.

Forma rectangular de un número complejo

La forma rectangular, por otro lado, es donde un número complejo se denota por sus respectivos componentes horizontal y vertical. En esencia, el vector en ángulo se toma como la hipotenusa de un triángulo rectángulo, descrito por las longitudes de los lados adyacentes y opuestos.

En lugar de describir la longitud y la dirección de un vector denotando la magnitud y el ángulo, se describe en términos de "qué tan lejos a la izquierda / derecha" y "qué tan arriba / abajo".

Estas figuras bidimensionales (horizontal y vertical) están simbolizadas por dos figuras numéricas. Para distinguir las dimensiones horizontal y vertical entre sí, la vertical tiene como prefijo una "i" minúscula (en matemáticas puras) o "j" (en electrónica).

Estas letras minúsculas no representan una variable física (como la corriente instantánea, también simbolizada por una letra minúscula "i"), sino que son operadores matemáticos. utilizado para distinguir el componente vertical del vector de su componente horizontal. Como un número complejo completo, las cantidades horizontal y vertical se escriben como una suma:(Figura siguiente)

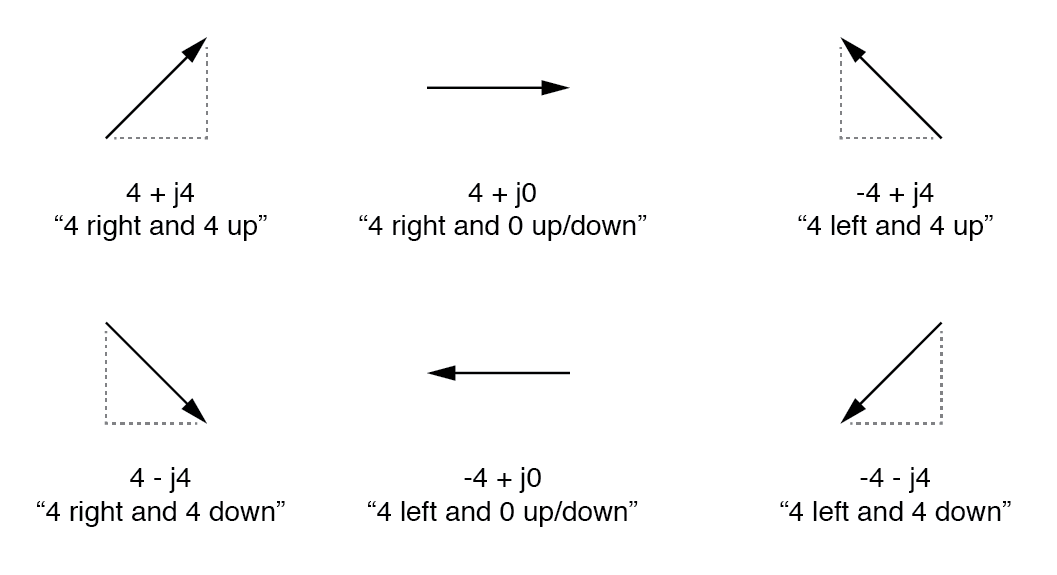
En forma "rectangular", la longitud y la dirección del vector se indican en términos de su tramo horizontal y vertical, el primer número representa la horizontal ("real") y el segundo número (con el prefijo "j") que representa las dimensiones verticales ("imaginarias").

El componente horizontal se conoce como real componente ya que esa dimensión es compatible con números normales, escalares ("reales"). El componente vertical se conoce como imaginario componente ya que esa dimensión se encuentra en una dirección diferente, totalmente ajena a la escala de los números reales. (Figura siguiente)

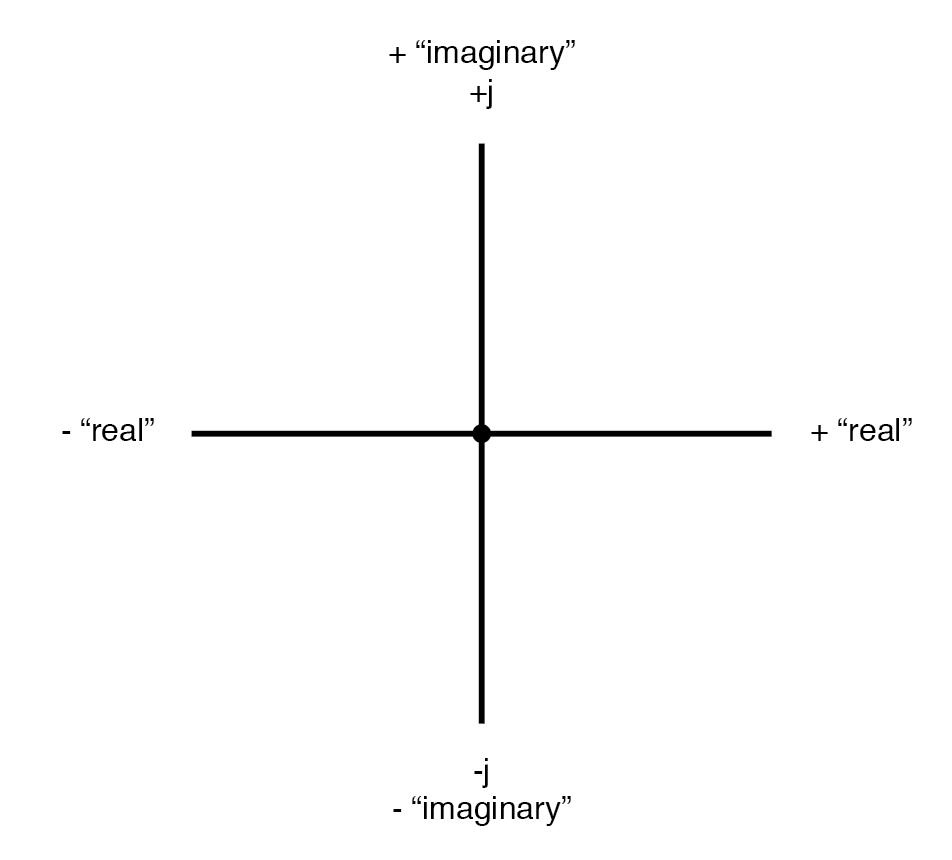
Brújula vectorial que muestra ejes reales e imaginarios.

El eje "real" del gráfico corresponde a la conocida recta numérica que vimos antes:la que tiene valores tanto positivos como negativos. El eje "imaginario" del gráfico corresponde a otra recta numérica situada a 90 ° de la "real".

Los vectores son cosas bidimensionales, debemos tener un "mapa" bidimensional sobre el cual expresarlos, por lo tanto, las dos líneas numéricas perpendiculares entre sí:(Figura siguiente)

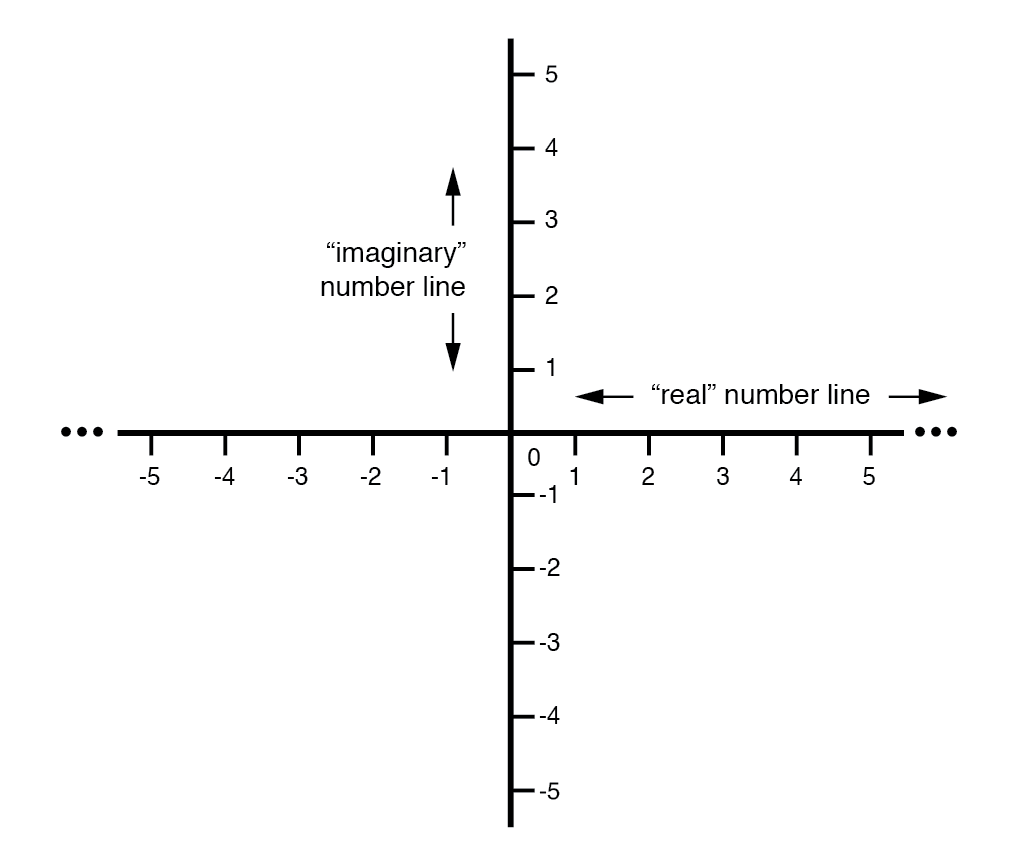
Brújula vectorial con líneas numéricas reales e imaginarias ("j").

Conversión de forma polar a forma rectangular

Cualquiera de los métodos de notación es válido para números complejos. La razón principal para tener dos métodos de notación es la facilidad de cálculo a mano, la forma rectangular que se presta a la suma y la resta, y la forma polar que se presta a la multiplicación y la división.

La conversión entre las dos formas de notación implica una simple trigonometría. Para convertir de polar a rectangular, encuentre el componente real multiplicando la magnitud polar por el coseno del ángulo y el componente imaginario multiplicando la magnitud polar por el seno del ángulo.

Esto puede entenderse más fácilmente dibujando las cantidades como lados de un triángulo rectángulo, la hipotenusa del triángulo representa el vector en sí (su longitud y ángulo con respecto a la horizontal constituyen la forma polar), los lados horizontal y vertical representan el " componentes rectangulares reales ”e“ imaginarios ”, respectivamente:(Figura siguiente)

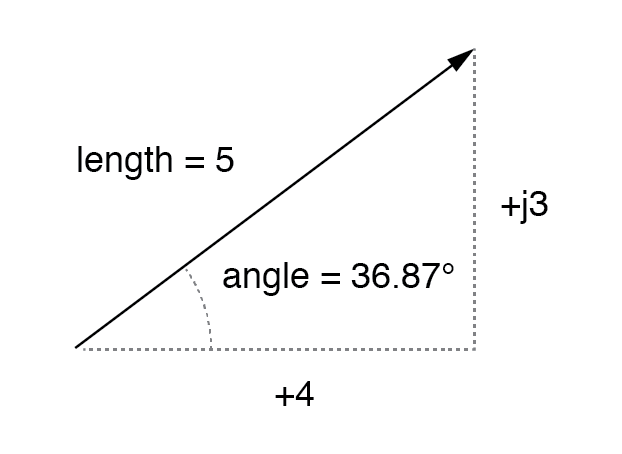
Vector de magnitud en términos de componentes reales (4) e imaginarios (j3).

Conversión de forma rectangular a forma polar

Para convertir de rectangular a polar, encuentre la magnitud polar mediante el uso del Teorema de Pitágoras (la magnitud polar es la hipotenusa de un triángulo rectángulo, y las componentes real e imaginaria son los lados adyacente y opuesto, respectivamente), y el ángulo por tomando el arcangente del componente imaginario dividido por el componente real:

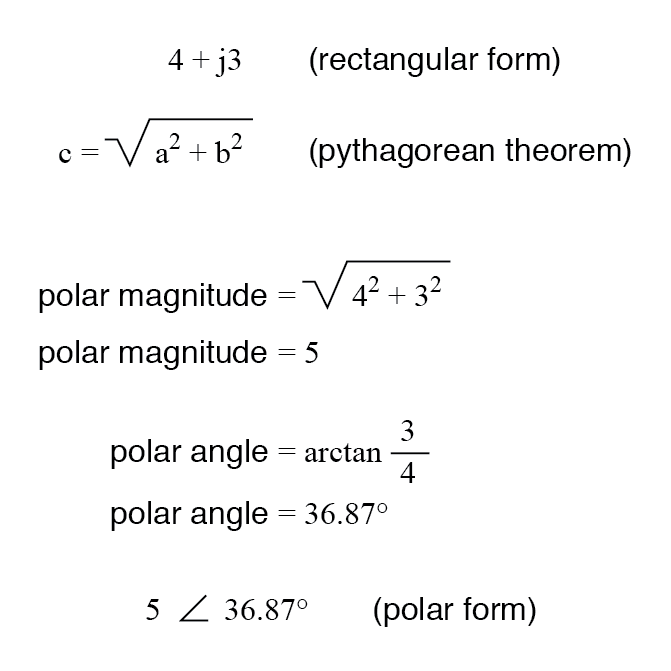
REVISAR:

• Polar La notación denota un número complejo en términos de la longitud de su vector y la dirección angular desde el punto de partida. Ejemplo:volar 45 millas ∠ 203 ° (oeste por suroeste).
• Rectangular la notación denota un número complejo en términos de sus dimensiones horizontal y vertical. Ejemplo:conduzca 41 millas al oeste, luego gire y conduzca 18 millas al sur.
• En notación rectangular, la primera cantidad es el componente "real" (dimensión horizontal del vector) y la segunda cantidad es el componente "imaginario" (dimensión vertical del vector). El componente imaginario está precedido por una "j" minúscula, a veces llamado el operador j .
• Las formas de notación polar y rectangular para un número complejo se pueden relacionar gráficamente en forma de triángulo rectángulo, con la hipotenusa representando el vector en sí (forma polar:hipotenusa longitud =magnitud; ángulo con respecto al lado horizontal =ángulo ), el lado horizontal representa el componente rectangular "real" y el lado vertical representa el componente rectangular "imaginario".

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de la fase de CA