Aritmética de números complejos

Dado que los números complejos son entidades matemáticas legítimas, al igual que los números escalares, se pueden sumar, restar, multiplicar, dividir, elevar al cuadrado, invertir y demás, como cualquier otro tipo de número.

Algunas calculadoras científicas están programadas para realizar directamente estas operaciones en dos o más números complejos, pero estas operaciones también se pueden realizar "a mano". Esta sección le mostrará cómo se realizan las operaciones básicas.

Es altamente recomendó que se equipe con una calculadora científica capaz de realizar funciones aritméticas fácilmente en números complejos. Hará que su estudio del circuito de CA sea mucho más agradable que si se viera obligado a hacer todos los cálculos por más tiempo.

Suma y resta de números complejos en forma rectangular

Sumar y restar con números complejos en forma rectangular es fácil. Para sumar, simplemente sume los componentes reales de los números complejos para determinar el componente real de la suma, y ​​sume los componentes imaginarios de los números complejos para determinar el componente imaginario de la suma:

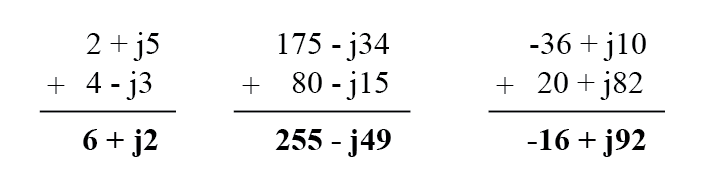
Al restar números complejos en forma rectangular, simplemente reste el componente real del segundo número complejo del componente real del primero para llegar al componente real de la diferencia, y reste el componente imaginario del segundo número complejo del componente imaginario de el primero en llegar el componente imaginario de la diferencia:

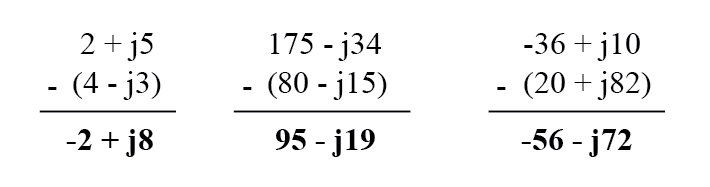
Multiplicación y división de números complejos en forma polar

Para la multiplicación y división a mano, polar es la notación preferida para trabajar. Al multiplicar números complejos en forma polar, simplemente multiplica las magnitudes polares de los números complejos para determinar la magnitud polar del producto y sumar los ángulos de los números complejos para determinar el ángulo del producto:

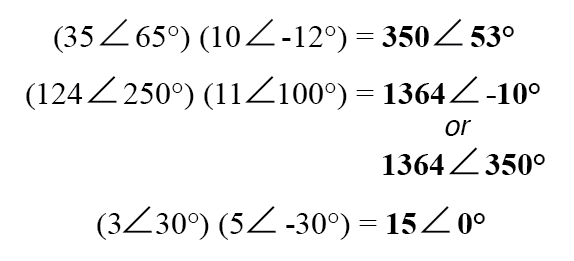
La división de números complejos en forma polar también es fácil:simplemente divida la magnitud polar del primer número complejo por la magnitud polar del segundo número complejo para llegar a la magnitud polar del cociente y reste el ángulo del segundo número complejo de el ángulo del primer número complejo que llega al ángulo del cociente:

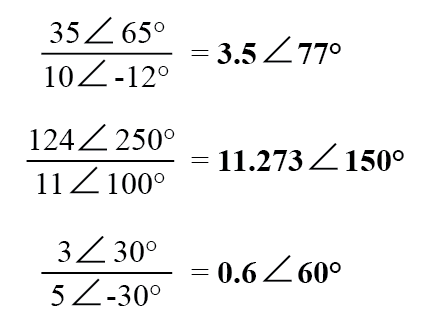
Para obtener el recíproco, o "invertir" (1 / x), un número complejo, simplemente divida el número (en forma polar) en un valor escalar de 1, que no es más que un número complejo sin componente imaginario (ángulo =0):

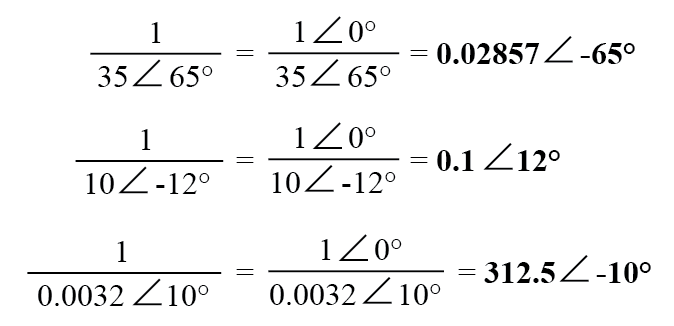
Estas son las operaciones básicas que necesitará saber para manipular números complejos en el análisis de circuitos de CA. Sin embargo, las operaciones con números complejos no se limitan a la suma, resta, multiplicación, división e inversión.

Prácticamente cualquier operación aritmética que se pueda realizar con números escalares se puede realizar con números complejos, incluidas potencias, raíces, resolución de ecuaciones simultáneas con coeficientes complejos e incluso funciones trigonométricas (aunque esto implica una perspectiva completamente nueva en trigonometría llamada funciones hiperbólicas que está mucho más allá del alcance de esta discusión).

Asegúrese de estar familiarizado con las operaciones aritméticas básicas de suma, resta, multiplicación, división e inversión, y tendrá pocos problemas con el análisis de circuitos de CA.

REVISAR:

• Para sumar números complejos en forma rectangular, sume los componentes reales y sume los componentes imaginarios. La resta es similar.
• Para multiplicar números complejos en forma polar, multiplica las magnitudes y suma los ángulos. Para dividir, divida las magnitudes y reste un ángulo del otro.

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de la fase de CA