Aritmética booleana

Comencemos nuestra exploración del álgebra booleana sumando números:

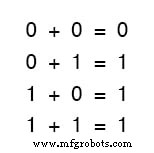
Las primeras tres sumas tienen mucho sentido para cualquiera que esté familiarizado con la suma elemental.

Sin embargo, la última suma es posiblemente responsable de más confusión que cualquier otra afirmación en electrónica digital, porque parece ir en contra de los principios básicos de las matemáticas.

Bueno, contradice los principios de suma para números reales, pero no para números booleanos.

Recuerde que en el mundo del álgebra de Boole, solo hay dos valores posibles para cualquier cantidad y para cualquier operación aritmética:1 o 0.

No existe el "2" dentro del alcance de los valores booleanos. Dado que la suma "1 + 1" ciertamente no es 0, debe ser 1 mediante el proceso de eliminación.

Tampoco importa cuántos o pocos términos sumemos. Considere las siguientes sumas:

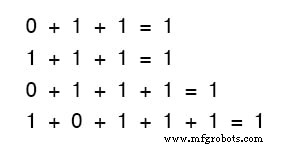
Puerta OR

Observe de cerca las sumas de dos términos en el primer conjunto de ecuaciones.

¿Ese patrón te suena familiar? ¡Debería! Es el mismo patrón de 1 y 0 que se ve en la tabla de verdad para una puerta OR.

En otras palabras, la suma booleana corresponde a la función lógica de una puerta "O", así como a los contactos del interruptor en paralelo:

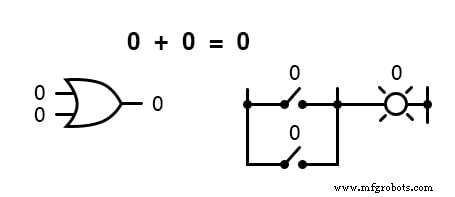
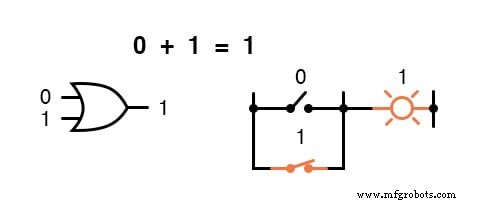
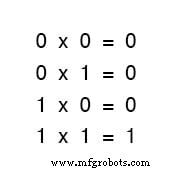
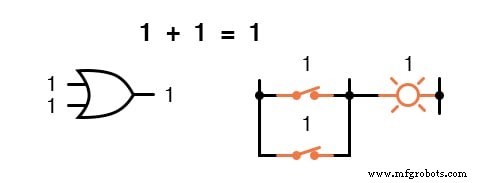
No existe tal cosa como la resta en el ámbito de las matemáticas booleanas.

La resta implica la existencia de números negativos: 5 - 3 es lo mismo que 5 + (-3) , y en álgebra de Boole las cantidades negativas están prohibidas.

Tampoco existe la división en las matemáticas booleanas, ya que la división no es más que una resta compuesta , de la misma manera que la multiplicación es suma compuesta .

Y puerta

La multiplicación es válida en el álgebra de Boole y, afortunadamente, es lo mismo que en el álgebra de números reales:cualquier cosa multiplicada por 0 es 0 y cualquier cosa multiplicada por 1 permanece sin cambios:

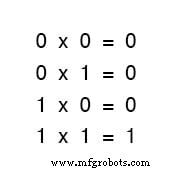
Este conjunto de ecuaciones también debería resultarle familiar:es el mismo patrón que se encuentra en la tabla de verdad para una puerta AND.

En otras palabras, la multiplicación booleana corresponde a la función lógica de un " Y ”Puerta, así como a los contactos del interruptor en serie:

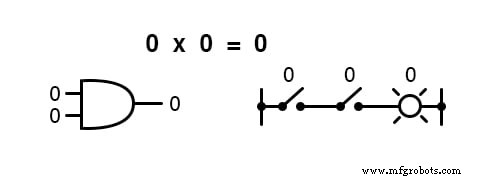
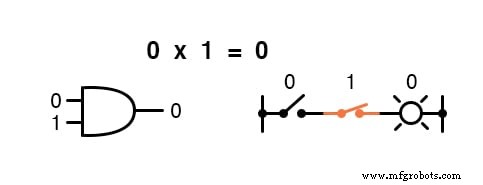
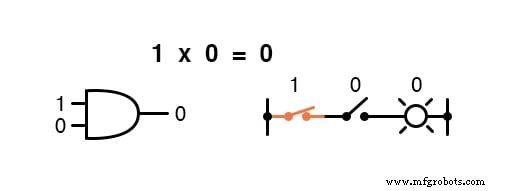
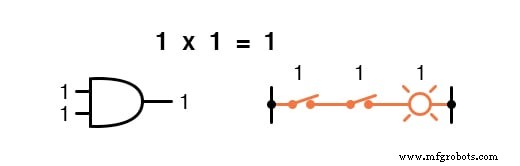
Como el álgebra "normal", el álgebra booleana usa letras alfabéticas para denotar variables.

Sin embargo, a diferencia del álgebra "normal", las variables booleanas son siempre letras MAYÚSCULAS, nunca minúsculas.

Debido a que solo pueden poseer uno de los dos valores posibles, 1 o 0 , todas y cada una de las variables tienen un complemento :lo contrario de su valor.

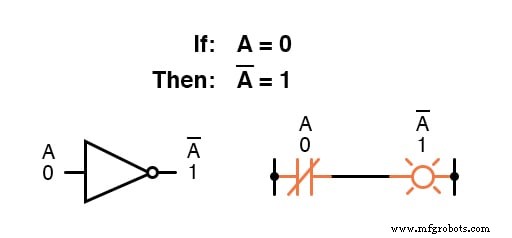
Por ejemplo, si la variable " A "Tiene un valor de 0 , luego el complemento de A tiene un valor de 1 .

La notación booleana usa una barra sobre el carácter de variable para denotar complementación, como esta:

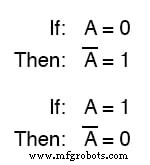
NO puerta

En forma escrita, el complemento de " A "Denotado como" A-no "O" Barra A ”. A veces, se usa un símbolo "principal" para representar la complementación.

Por ejemplo, A ’Sería el complemento de A , muy parecido a usar un símbolo primo para denotar diferenciación en cálculo en lugar de la notación fraccionaria d / dt .

Sin embargo, por lo general, el símbolo de "barra" encuentra un uso más generalizado que el símbolo " principal ”, Por razones que serán más evidentes más adelante en este capítulo.

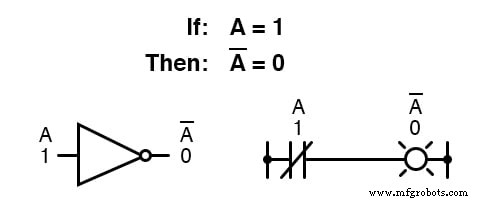
La complementación booleana encuentra equivalencia en la forma de la puerta NOT , o un interruptor o relé normalmente cerrado:

La definición básica de cantidades booleanas ha llevado a reglas simples de suma y multiplicación, y ha excluido tanto la resta como la división como operaciones aritméticas válidas.

Tenemos una simbología para denotar variables booleanas y sus complementos. En la siguiente sección procederemos a desarrollar identidades booleanas.

REVISAR:

• La suma booleana es equivalente a OR función lógica, así como contactos de interruptores paralelos.
• La multiplicación booleana es equivalente a Y función lógica, así como contactos de interruptores en serie.
• La complementación booleana es equivalente a NOT función lógica, así como normalmente cerrado contactos de relé.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de álgebra booleana