Mapas de Karnaugh, tablas de verdad y expresiones booleanas

¿Quién desarrolló el mapa de Karnaugh?

Maurice Karnaugh, un ingeniero de telecomunicaciones, desarrolló el mapa de Karnaugh en Bell Labs en 1953 mientras diseñaba circuitos de conmutación telefónica basados ​​en lógica digital.

El uso del mapa de Karnaugh

Ahora que hemos desarrollado el mapa de Karnaugh con la ayuda de los diagramas de Venn, pongámoslo en práctica. Mapas de Karnaugh reducir La lógica funciona más rápida y fácilmente en comparación con el álgebra de Boole. Por reducir nos referimos a simplificar, reduciendo el número de puertas y entradas.

Nos gusta simplificar la lógica al menor costo Formulario para ahorrar costes mediante la eliminación de componentes. Definimos el costo más bajo como el número más bajo de puertas con el número más bajo de entradas por puerta.

Si se les da la opción, la mayoría de los estudiantes simplifican la lógica con mapas de Karnaugh en lugar de usar álgebra booleana una vez que aprenden esta herramienta.

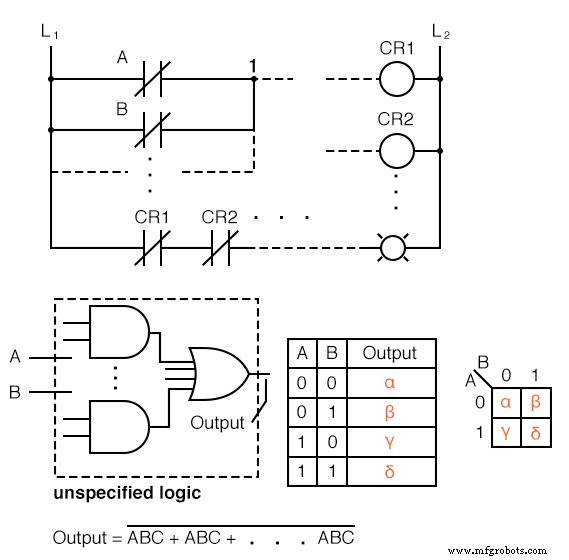
Mostramos cinco elementos individuales arriba, que son solo diferentes formas de representar lo mismo:una función lógica digital arbitraria de 2 entradas. Primero está la lógica de escalera de relés, luego las puertas lógicas, una tabla de verdad, un mapa de Karnaugh y una ecuación booleana.

El caso es que cualquiera de estos es equivalente. Dos entradas A y B puede tomar valores de 0 o 1 , alto o bajo, abierto o cerrado, Verdadero o Falso, según sea el caso. Hay 2 ² =4 combinaciones de insumos que producen una salida. Esto es aplicable a los cinco ejemplos.

Estas cuatro salidas se pueden observar en una lámpara en la lógica de escalera de relés, en una sonda lógica en el diagrama de puerta. Estos resultados pueden registrarse en la tabla de verdad o en el mapa de Karnaugh. Mire el mapa de Karnaugh como una tabla de verdad reordenada.

La salida de la ecuación booleana puede calcularse mediante las leyes del álgebra booleana y transferirse a la tabla de verdad o al mapa de Karnaugh.

¿Cuál de las cinco descripciones lógicas equivalentes deberíamos usar? El que sea más útil para la tarea a realizar.

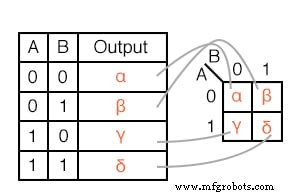
Los resultados de una tabla de verdad se corresponden uno a uno con las entradas del mapa de Karnaugh. Comenzando en la parte superior de la tabla de verdad, las entradas A =0, B =0 producen una salida α.

Tenga en cuenta que esta misma salida α se encuentra en el mapa de Karnaugh en la dirección de celda A =0, B =0, esquina superior izquierda del mapa K donde se cruzan la fila A =0 y la columna B =0. Las otras salidas de la tabla de verdad β, χ, δ de las entradas AB =01, 10, 11 se encuentran en las ubicaciones correspondientes del K-map.

A continuación, mostramos las regiones adyacentes de 2 celdas en el mapa K de 2 variables con la ayuda del diagrama de Venn rectangular anterior, como las regiones booleanas.

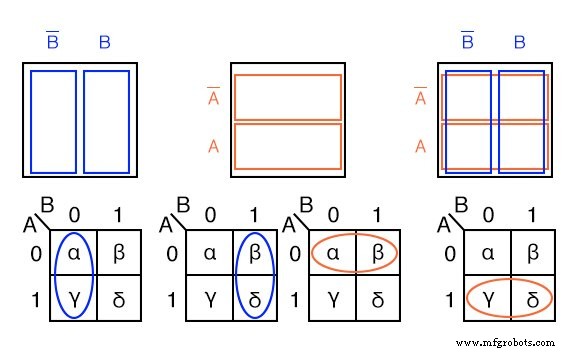
Las celdas α y χ son adyacentes en el mapa K como elipses en el mapa K más a la izquierda a continuación. Refiriéndose a la tabla de verdad anterior, este no es el caso. Hay otra entrada de la tabla de verdad (β) entre ellos. Lo que nos lleva al punto de organizar el mapa K en una matriz cuadrada, las celdas con cualquier variable booleana en común deben estar cerca una de la otra para presentar un patrón que salte a la vista.

Para las celdas α y χ tienen la variable booleana B ’ en común. Lo sabemos porque B =0 (igual que B ’ ) para la columna encima de las celdas α y χ. Compare esto con el diagrama de Venn cuadrado sobre el mapa K.

Una línea de razonamiento similar muestra que β y δ tienen B booleanos (B =1) en común. Entonces, α y β tienen A ’ booleanos (A =0) en común. Finalmente, χ y δ tienen A booleanos (A =1) en común. Compare los dos últimos mapas con el diagrama de Venn cuadrado del medio.

Para resumir, buscamos elementos comunes de variables booleanas entre celdas. El mapa de Karnaugh está organizado de modo que podamos ver esa similitud. Probemos algunos ejemplos.

Ejemplos

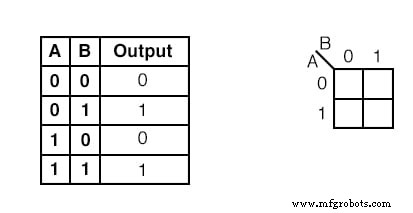
Ejemplo:

Transfiera el contenido de la tabla de verdad al mapa de Karnaugh anterior.

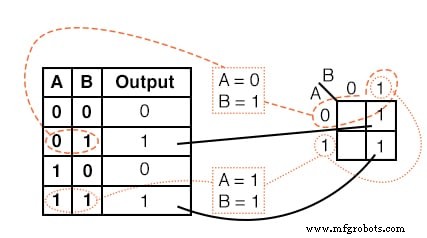
Solución:

La tabla de verdad contiene dos 1 s. el mapa K debe tener ambos. localizar el primer 1 en la segunda fila de la tabla de verdad anterior.

• anote la dirección AB de la tabla de verdad
• ubicar la celda en el mapa K que tiene la misma dirección
• colocar un 1 en esa celda

Repite el proceso para 1 en la última línea de la tabla de verdad.

Ejemplo:

Para el mapa de Karnaugh en el problema anterior, escriba la expresión booleana. La solución está a continuación.

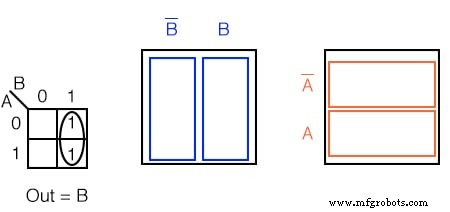
Solución:

Busque celdas adyacentes, es decir, arriba o al lado de una celda. Las celdas diagonales no son adyacentes. Las celdas adyacentes tendrán una o más variables booleanas en común.

• Agrupe (encierre en un círculo) los dos 1 s en la columna
• Busque la (s) variable (s) en la parte superior y / o lateral que sean iguales para el grupo. Escriba esto como el resultado booleano. Es B en nuestro caso.
• Ignore las variables que no son iguales para un grupo de celdas. En nuestro caso, A varía, es tanto 1 como 0, ignore el booleano A.
• Ignore cualquier variable que no esté asociada con celdas que contengan 1. B ’ no tiene nadie debajo de él. Ignorar B ’
• Resultado Fuera =B

Esto podría ser más fácil de ver si se compara con los diagramas de Venn de la derecha, específicamente con B columna.

Ejemplo:

Escriba la expresión booleana para el mapa de Karnaugh a continuación.

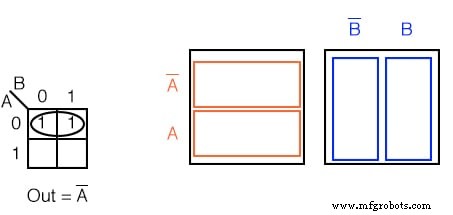
Solución: (arriba)

• Agrupe (encierre en un círculo) los dos unos en la fila
• Busque la (s) variable (s) que son iguales para el grupo, Out =A ’

Ejemplo:

Para la tabla de Verdad a continuación, transfiera las salidas al Karnaugh, luego escriba la expresión booleana para el resultado.

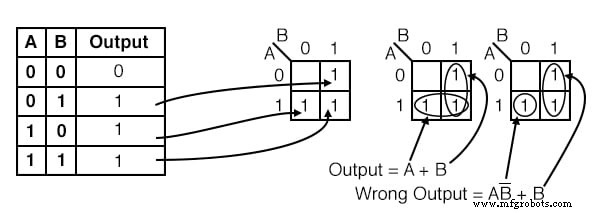
Solución:

Transferir el 1 s desde las ubicaciones en la tabla de Verdad a las ubicaciones correspondientes en el K-map.

• Agrupe (encierre en un círculo) los dos 1 en la columna debajo de B =1
• Agrupe (encierre en un círculo) los dos unos en la fila a la derecha de A =1
• Escriba el término del producto para el primer grupo = B
• Escriba el término de producto para el segundo grupo = A
• Escriba la suma de los productos de los dos términos anteriores Salida =A + B

La solución del mapa K en el medio es la solución más simple o de menor costo. Una solución menos deseable está en el extremo derecho. Después de agrupar los dos 1 s, cometemos el error de formar un grupo de 1 celda. La razón por la que esto no es deseable es que:

• La celda individual tiene un término de producto de AB ’
• La solución correspondiente es Salida =AB ’+ B
• Esta no es la solución más simple

La forma de recoger este single 1 es formar un grupo de dos con el 1 a la derecha, como se muestra en la línea inferior del mapa K central, aunque este 1 ya se ha incluido en el grupo de columnas ( B ). Se nos permite reutilizar las células para formar grupos más grandes. De hecho, es deseable porque conduce a un resultado más simple.

Necesitamos señalar que cualquiera de las soluciones anteriores, Salida o Salida incorrecta, son lógicamente correctas. Ambos circuitos producen la misma salida. Se trata de que el circuito anterior sea la solución de menor costo.

Ejemplo:

Complete el mapa de Karnaugh para la expresión booleana a continuación, luego escriba la expresión booleana para el resultado.

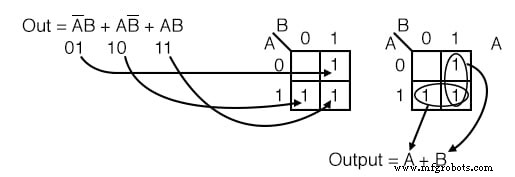
Solución: (arriba)

La expresión booleana tiene tres términos de producto. Habrá un 1 ingresado para cada término de producto. Aunque, en general, el número de 1 s por término de producto varía con el número de variables en el término de producto en comparación con el tamaño del K-map.

El término del producto es la dirección de la celda donde 1 es ingresado. El primer término de producto, A'B , corresponde al 01 celda en el mapa. Un 1 se ingresa en esta celda. Los otros dos términos P se ingresan para un total de tres 1s

A continuación, proceda a agrupar y extraer el resultado simplificado como en el problema anterior de la tabla de verdad.

Ejemplo:

Simplifique el diagrama lógico a continuación.

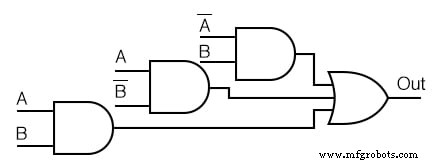
Solución: (Figura siguiente)

• Escriba la expresión booleana para el diagrama lógico original como se muestra a continuación
• Transfiera los términos del producto al mapa de Karnaugh
• Forme grupos de celdas como en los ejemplos anteriores
• Escriba una expresión booleana para grupos como en los ejemplos anteriores
• Dibujar un diagrama lógico simplificado

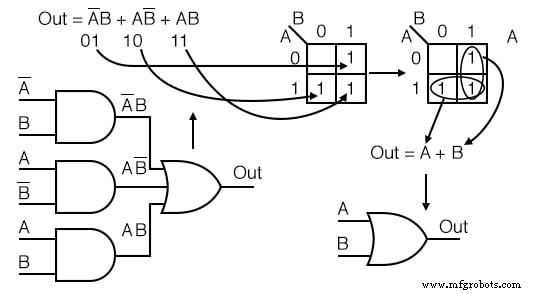
Ejemplo: Simplifique el diagrama lógico a continuación.

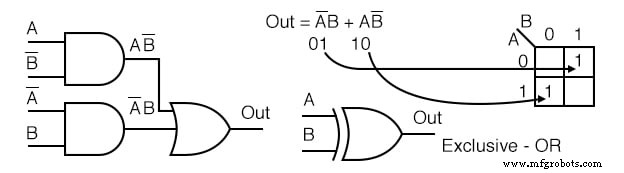
Solución:

• Escriba la expresión booleana para el diagrama lógico original que se muestra arriba
• Transfiera los términos del producto al mapa de Karnaugh.
• No es posible formar grupos.
• No es posible simplificar; déjelo como está.

No es posible una simplificación lógica para el diagrama anterior. Esto sucede a veces. Ni los métodos de los mapas de Karnaugh ni el álgebra de Boole pueden simplificar aún más esta lógica.

Mostramos un símbolo esquemático de O exclusivo arriba; sin embargo, esta no es una simplificación lógica. Simplemente hace que un diagrama esquemático se vea mejor.

Dado que no es posible simplificar la lógica OR exclusivo y se usa ampliamente, los fabricantes la proporcionan como un circuito integrado básico (7486).

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de mapeo de Karnaugh
• Hoja de trabajo de álgebra booleana
• Hoja de trabajo de puertas lógicas básicas