Giro y rotación orbital del dímero plasmónico impulsado por luz circularmente polarizada
Resumen
Se estudiaron teóricamente el espín potenciado por plasmón y la rotación orbital del dímero Au, dos nanopartículas unidas ópticamente (NP), inducidas por una luz polarizada circularmente (CP) (onda plana o haz gaussiano). A través de las prestaciones optomecánicas de las fuerzas ópticas y los momentos de torsión, se investigó el acoplamiento de giro-órbita (SOC) longitudinal / transversal de los campos electromagnéticos retorcidos. Las fuerzas ópticas muestran que para la interacción de largo alcance, existen algunas órbitas de equilibrio estable para la rotación, donde las distancias entre partículas de equilibrio estable son casi los múltiplos enteros de la longitud de onda en el medio. Además, el par de giro óptico hace que cada NP gire individualmente. Para una onda plana, las hélicidades del giro longitudinal y la rotación orbital de los NP acoplados son las mismas en la órbita de equilibrio estable, lo que es consistente con la destreza de la onda plana. Por el contrario, para un rayo gaussiano enfocado, la helicidad de la rotación orbital del dímero podría ser opuesta a la mano de la luz incidente debido al par orbital óptico negativo en la distancia entre partículas de equilibrio estable; además, el giro transversal de cada NP se vuelve profundo. Estos resultados demuestran que el SOC longitudinal / transversal se induce significativamente debido al campo óptico retorcido. Para la interacción de corto alcance, se induce la atracción mutua entre dos NP, asociada con la trayectoria de giro y espiral; eventualmente, los dos NP chocarán. El límite de la distancia entre partículas entre las interacciones de corto y largo alcance es aproximadamente de media longitud de onda en el medio.
Antecedentes
La unión óptica de dos micropartículas (MP) o nanopartículas (NP) irradiadas por una luz polarizada linealmente (LP) es un comportamiento optomecánico importante, que es el resultado de la interacción luz-materia [1, 2, 3, 4]. Hay varias distancias entre partículas de equilibrio estable entre el dímero ligado ópticamente; estas distancias son casi los múltiplos enteros de la longitud de onda en el medio [3, 4, 5, 6]. Además, la orientación del dímero es perpendicular a la polarización de la luz LP. Como la distancia entre partículas está cerca de múltiplos enteros de la longitud de onda, los fotones dispersos entre las partículas hacen una interferencia constructiva para inducir una fuerza de unión. También se estudiaron los fenómenos de la matriz ópticamente unida de múltiples MP de sílice o Ag NP [7, 8, 9, 10]. Para la iluminación de una onda plana polarizada circularmente (CP), Haefner et al. informó que las helicidades del espín longitudinal y la rotación orbital de las dos NP de sílice acopladas con un tamaño de 100-700 nm son las mismas que las de la luz incidente [11]. Recientemente, Sule et al. encontró experimentalmente que la helicidad de la rotación orbital de dos Ag NP de un radio de 75 nm unidas por la fuerza óptica es opuesta a la mano de un haz CP Gaussiano enfocado de 790 nm en el agua [12]; es decir, el dímero de Ag sufre un par orbital óptico negativo [13, 14]. Además, la rotación de la órbita medida fue de unos 4 kHz [12]. Por otro lado, también se ha estudiado el giro de un solo Au NP de radio de 100 nm inducido por un haz CP Gaussiano [15,16,17,18]. La rotación de giro medida fue de hasta 3,5 kHz [15]. En las últimas décadas, el acoplamiento de espín-órbita longitudinal / transversal (SOC) del campo óptico atrae mucha atención [19,20,21,22,23]. Por ejemplo, un haz de vórtice óptico (p. Ej., Haces Laguerre-Gaussianos de alto orden con polarizaciones azimutales o radiales) o un haz CP Gaussiano altamente enfocado se puede utilizar para inducir el SOC [24,25,26,27,28,29,30 , 31,32,33,34]. El campo electromagnético (EM) retorcido del haz de vórtice óptico transporta tanto el momento angular de giro como el momento angular orbital, induciendo así el giro longitudinal / transversal y la rotación orbital de un NP de sonda cercano [18,19,20,21,22,23 , 24,25,26]. En particular, el SOC en el campo cercano de NP de Au o Ag es más significativo debido al movimiento colectivo de electrones libres en estas NP (efecto plasmón) [28,29,30,31].
En este artículo estudiamos teóricamente los comportamientos optomecánicos (fuerzas ópticas y pares) de dos NP de Au acopladas (dímero) soportadas por un sustrato, que son inducidas por la iluminación de un haz de CP Gaussiano. El sustrato es necesario para confinar estos NP independientes que se mueven en el plano focal, en lugar de flotar en el espacio 3D. El método multipolo múltiple (MMP) se utiliza para simular el campo EM numéricamente y luego para analizar el orbital óptico y los pares de giro en el dímero ligado ópticamente [35, 36]. A través de las respuestas optomecánicas del dímero, se manifestará el SOC longitudinal / transversal. En particular, también se investigará la condición para generar un par orbital óptico negativo en el dímero.
Métodos
La Figura 1 muestra la configuración de un par de NP de Au idénticas sostenidas por un sustrato e irradiadas por una luz CP de izquierda (LH) normalmente incidente (onda plana o haz gaussiano), donde d representa la distancia entre partículas. La cintura del rayo gaussiano se indica con w 0 , y el plano focal está en la sección transversal central de las NP de Au. Las formulaciones del campo eléctrico de onda plana y haz gaussiano se adjuntan como Apéndice. Suponemos que el índice de refracción del sustrato es el mismo que el del medio circundante, el agua. Por tanto, la luz reflejada no se inducirá en la interfaz entre el medio y el sustrato; el campo óptico no se ve perturbado por la existencia del sustrato [37]. Por otro lado, la existencia del sustrato sirve como un confinamiento para soportar los NP que se mueven sobre el sustrato. El método multipolar (MMP) se utiliza para simular el campo electromagnético inducido [17, 18, 35, 36]. Las fuerzas ópticas F j ejercido sobre el j th NP ( j =1, 2) están expresados por
$$ {\ mathbf {F}} ^ j ={\ int} _ {S_j} \ mathbf {T} \ cdot \ mathbf {n} \ kern0.1em \ mathrm {d} S. $$ (1)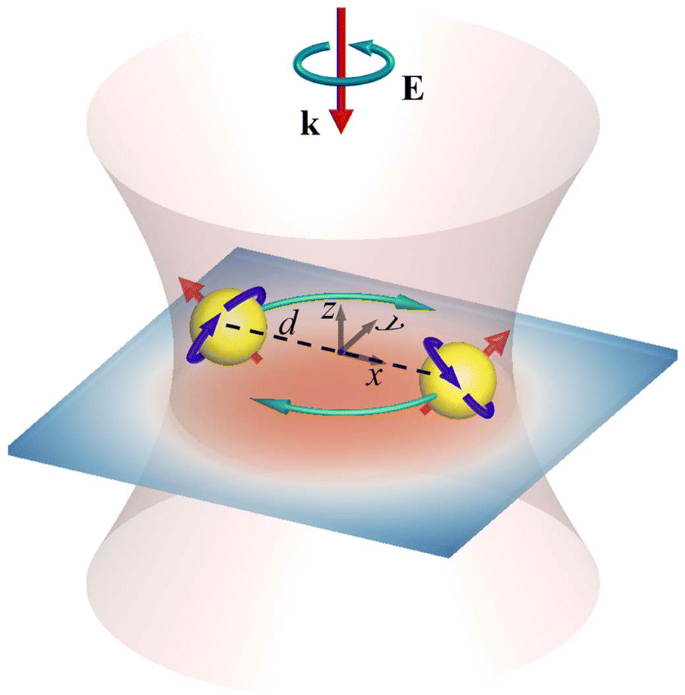
Configuración de un par de NP con un sustrato de soporte, irradiado por un haz de cintura LH CP Gaussiano normalmente incidente (w0). Las secciones transversales centrales de estos NP están en el plano focal del haz de Gauss, y d es la distancia entre los centros de los NP. Las respuestas optomecánicas son la rotación orbital longitudinal y el giro longitudinal / transversal
Aquí, n es el vector normal hacia afuera en la superficie de j th NP y T es el tensor de tensión de Maxwell promedio en el tiempo expresado como
$$ \ mathbf {T} =\ frac {1} {2} \ operatorname {Re} \ left \ {\ varepsilon \ mathbf {E} \ overline {\ mathbf {E}} + \ mu \ mathbf {H} \ overline {\ mathbf {H}} - \ frac {1} {2} \ left (\ varepsilon \ mathbf {E} \ cdot \ overline {\ mathbf {E}} + \ mu \ mathbf {H} \ cdot \ overline {\ mathbf {H}} \ derecha) \; \ mathbf {I} \ derecha \}. $$ (2)En Eq. (2), yo es una matriz identidad de 3 × 3, la barra superior denota el conjugado complejo y Re la parte real [17, 18, 35, 36]. Aquí, ε y μ son la permitividad y permeabilidad del medio circundante. Observe que la E y H son el campo total exterior usado para Eq. (2). De hecho, T es también el flujo de momento lineal promediado en el tiempo. A lo largo de este artículo, las fuerzas ópticas se expresan en las coordenadas cilíndricas:radial, azimutal y z -componentes del eje. La fuerza radial puede indicar la atracción o repulsión entre los dos NP y la fuerza azimutal la helicidad de la revolución orbital de NP.
Por otro lado, el par de giro óptico en el j th NP ( j =1, 2) para el hilado de NP individuales está dado por,
$$ {\ mathbf {M}} ^ j ={\ int} _ {S_j} {\ mathbf {x}} ^ j \ times \ mathbf {T} \ cdot \ mathbf {n} \; \ mathrm {d} S. $$ (3)En Eq. (3), x j × T es el flujo de momento angular y x j es el vector de posición relativa de un punto x en la superficie S j con respecto al centro de masa \ ({\ mathbf {x}} _ c ^ j \) de j th NP; \ ({\ mathbf {x}} ^ j =\ mathbf {x} - {\ mathbf {x}} _ c ^ j \). La dirección longitudinal está designada para ser paralela al eje óptico (digamos z dirección) de la luz incidente, y la dirección transversal es perpendicular al eje óptico. Por otro lado, el par orbital óptico longitudinal en el z dirección en cada NP, causada por la fuerza óptica azimutal, se define como F θ d / 2 en las coordenadas cilíndricas. La permitividad relativa de Au en λ =800 nm usado en la simulación es (- 24.062, 1.507) [38].
Resultados y discusión
Estudiamos las fuerzas ópticas y los momentos de torsión ejercidos sobre dos NP de Au idénticas con un radio de 100 nm irradiadas por una onda plana LH CP normalmente incidente o un rayo gaussiano enfocado en el plano focal. El medio circundante es el agua. La fluencia de la onda plana o haz gaussiano en el centro es de 25 MW / cm 2 . Los centros de los dos NP independientes, sostenidos por un sustrato virtual, pueden moverse en el xy plano (plano focal). Las fuerzas ópticas ( F r , F θ ) versus la distancia entre partículas d para una onda plana CP o un rayo gaussiano enfocado con una cintura de 500 nm de λ =800 nm se muestran en la Fig. 2a, b, respectivamente. La sección transversal central de estos NP está en el plano focal del haz de Gauss. La Figura 2a indica que para una onda plana, hay varias distancias entre partículas de equilibrio estable con F r =0 y pendiente negativa; el primero d 1 está a 603 nm y el segundo d 2 a 1204 nm. Estas distancias entre partículas de "equilibrio estable" son casi los múltiplos enteros de la longitud de onda en el medio; es decir, d m = mλ / n , donde n es el índice de refracción de medio y m =1, 2, 3 ... Es el resultado de la interacción luz-materia de largo alcance causada por la fuerza de unión óptica. Sugiere que hay un resorte óptico que conecta los dos NP; la fuerza restauradora F r del resorte óptico mantiene las NP separadas entre sí en estas distancias entre partículas de equilibrio estable. Para el caso del haz gaussiano, las dos primeras distancias entre partículas en equilibrio estable d 1 y d 2 son 585 y 1131 nm respectivamente, como se muestra en la Fig. 2b, ligeramente más pequeñas que las de una onda plana debido a la fuerza del gradiente inducida por el rayo gaussiano.
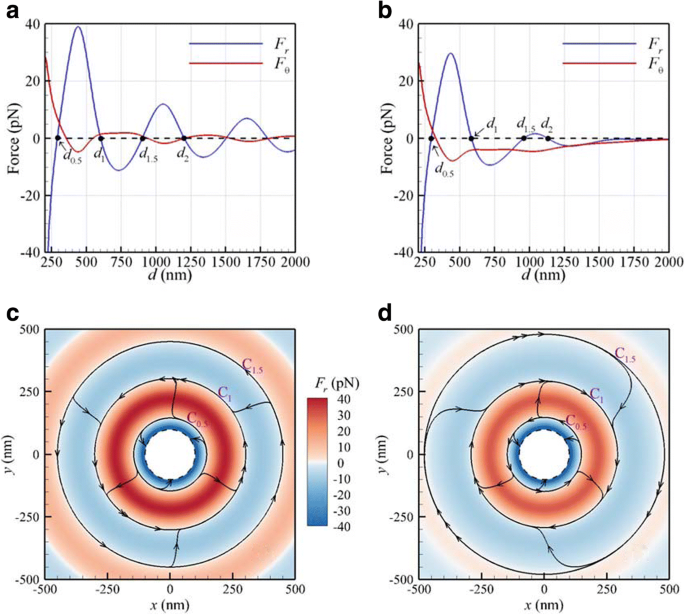
Fuerzas ópticas ( F r , F θ ) versus d para λ =800 nm por CP a onda plana y b Haz gaussiano con una cintura de 500 nm en el plano focal. Los mapas de líneas aerodinámicas 2D de fuerza óptica ( F r , F θ ) inducida por CP c onda plana y d Haz gaussiano. La barra de color representa la amplitud de F r . El anillo punteado es el círculo límite de los centros de dos NP donde los NP están en contacto
De hecho, el par orbital longitudinal F θ d / 2 hará que estos NP giren en órbitas con diámetros de d 1 y d 2 . Para los casos con el rayo gaussiano, las órbitas estarán centradas en el eje del rayo. El signo de la fuerza óptica azimutal ( F θ ) indica que la rotación orbital longitudinal (revolución) en la primera órbita de equilibrio estable inducida por el haz de Gauss es opuesta a la de una onda plana. Esto muestra que la F negativa θ del haz CP Gaussiano genera un par orbital negativo F θ d 1 / 2 en la primera órbita de equilibrio estable; lo que es más importante, la helicidad de la rotación orbital del dímero Au es opuesta a la lateralidad de la luz CP incidente [12]. También es interesante señalar que F θ es siempre negativo como d > 300 nm para los casos con haz gaussiano; El fenómeno de la rotación inversa (revolución) de los NP ópticamente ligados, debido al par orbital negativo, se observa fácilmente en los sistemas de pinzas ópticas. El par orbital óptico negativo podría atribuirse al campo EM retorcido del haz de Gauss [23].
Según la ley de Stokes de una esfera impulsada por una fuerza F moverse en un fluido viscoso, la velocidad terminal v T es v T = F / (6 πrη ), donde η es la viscosidad dinámica del agua (0,001 kg / m s). Este es el resultado de la fuerza aplicada equilibrada por la fuerza de arrastre de un fluido viscoso [39]. Según la ley de Stokes, el vector de velocidad terminal de un NP en un medio viscoso es proporcional a la fuerza aplicada [39]. Por lo tanto, usamos el campo de fuerza óptico para obtener las líneas de corriente, que son casi equivalentes a las trayectorias de estos NP. Además, los mapas de líneas de flujo 2D obtenidos directamente del campo de vector de fuerza óptica ( F r , F θ ) ejercida sobre NP se representan en la Fig. 2c, d para onda plana y haz gaussiano respectivamente, donde la barra de color representa la amplitud de F r . Tenga en cuenta que la tangente de la línea de corriente en cada punto es paralela al vector de fuerza óptica y, por lo tanto, también es paralela a la velocidad de NP. Para un rango de distancia entre partículas pequeño ( d < d 0.5 ), la fuerza óptica radial F r es negativo, por lo que estos dos NP se atraerán entre sí para colisionar eventualmente, como se muestra en la Fig. 2c, d. El anillo punteado es el círculo límite de los centros de dos NP donde los NP están en contacto. El anillo interior (azul) es una región de interacción de corto alcance. El anillo interior C 0.5 entre el anillo interior (azul, con F negativo r ) y el segundo anillo (rojo, con F positivo r ) es la línea fronteriza entre las regiones de interacción de corto y largo alcance del dímero de Au; el diámetro de C 0.5 es d 0.5 =291 nm en la Fig. 2c y d 0.5 =296 nm en la Fig. 2d. A largo plazo ( d 0.5 < d < d 1.5 ), las fuerzas ópticas radiales y azimutales impulsan a los dos NP acoplados a acercarse a la primera órbita de equilibrio estable C 1 con un diámetro d 1 debido al efecto de la fuerza de unión óptica. El dímero de Au ópticamente unido gira en sentido antihorario (CCW) a lo largo de la órbita C 1 ( d 1 =603 nm) en la Fig. 2c, mientras que a lo largo de C 1 ( d 1 =585 nm) en el sentido de las agujas del reloj (CW) en la Fig. 2d. La rotación anterior es la misma que la orientación de la luz incidente causada por el par orbital positivo ( F θ > 0), y este último es inverso debido al par orbital negativo ( F θ <0). De acuerdo con nuestro análisis del espectro de la sección transversal de dispersión de un dímero con una distancia de equilibrio estable de 603 nm irradiado por una onda plana CP (no se muestra aquí), la resonancia de plasmón de superficie de acoplamiento (SPR) del dímero ligado ópticamente está casi en 800 nm correspondiente a la luz incidente, que está fuera de resonancia de un solo NP (530 nm). En general, la SPR de acoplamiento de un dímero depende de la distancia entre partículas; cuanto mayor es la distancia, más se desplaza hacia el rojo el SPR de acoplamiento del dímero. Si usamos un haz gaussiano de longitud de onda más larga (por ejemplo, 1064 nm), la distancia entre partículas de equilibrio estable aumenta. Sin embargo, a medida que la distancia entre los dos NP se vuelve demasiado grande, el efecto de acoplamiento óptico disminuye, por lo que el SPR de acoplamiento desaparece gradualmente. En consecuencia, la SPR de un solo NP a 530 nm se vuelve dominante.
Para un NP de Au de radio de 100 nm que se mueve a lo largo de una órbita con un diámetro d y una velocidad angular Ω z , la velocidad es Ω z d / 2 = F θ / ( 6πrμ ). Si se aplica el rayo gaussiano ( F θ =- 4 pN), la velocidad angular Ω z (ciclos por segundo) a lo largo de C 1 es de aproximadamente - 7 kHz. El orden de magnitud es consistente con el resultado experimental [12]; la velocidad angular de la rotación orbital de dos Ag NP de r =75 nm irradiado por el haz de Gauss con 14 mW es - 4 kHz. Si d 1.5 < d < d 2.5 , estos NP se acercarán y rotarán a lo largo de la órbita secundaria de equilibrio estable C 2 (no se muestra aquí). Tenga en cuenta que para estos casos la fuerza óptica de F z es negativo empujar estos NP hacia abajo debido a la presión de radiación; F z =- 161,3 pN para onda plana y - 117,2 pN para el haz de Gauss. Esto infiere que la fuerza de reacción del sustrato de soporte es necesaria para equilibrar la fuerza óptica impulsora de F z . En consecuencia, las fuerzas resultantes en z la dirección sobre estos NP es cero; estos dos NP están confinados a moverse en el xy plano del plano focal.
Por otro lado, la Fig. 3a, b muestra los pares de giro ópticos ( M r , M θ , M z ) versus d inducida por una onda plana y un rayo gaussiano en el plano focal, respectivamente. Dado que los resultados de estos dos NP son los mismos, aquí solo se representa un conjunto de pares de giro ópticos. Los dos primeros ( M r , M θ ) son los pares de giro transversales, y los últimos M z es el longitudinal. Se encuentra que la helicidad del par de giro longitudinal es la misma que la destreza de la luz incidente para ambos casos. Esto se debe a que el momento angular de los fotones absorbidos de la luz CP incidente se transfiere a estos NP para el giro y la rotación orbital. Es interesante señalar que los pares de giro óptico transversal ( M r , M θ ) inducidos por un rayo gaussiano son significativamente grandes, en comparación con los de la onda plana. Esto podría atribuirse a los componentes transversales del campo EM retorcido en el plano focal de un rayo gaussiano. Además, las magnitudes máximas de los pares de giro transversales ópticos ocurren aproximadamente en la primera órbita de equilibrio estable C 1 ( d 1 =585 nm), como se muestra en la Fig. 3b. Según la ley de Stokes de una esfera giratoria girada por un par M en fluido viscoso, la velocidad angular terminal de la esfera es ω T = M / (8 πr 3 μ ) [18]. Por lo tanto, las magnitudes de las velocidades angulares de giro longitudinal / transversal de NP en C 1 son aproximadamente 10 kHz, de los cuales los órdenes de magnitud están de acuerdo con la velocidad de giro longitudinal medida [15], aproximadamente 3,5 kHz. En resumen, los fenómenos anteriores, como se muestra en las Figs. 2b y 3b, demuestran que la rotación orbital longitudinal va acompañada de giros longitudinales / transversales. El movimiento de los dos NP acoplados es similar al de un sistema de estrella binaria, donde las fuerzas ópticas proporcionan las fuerzas impulsoras orbitales y de unión para estos NP, así como los pares de giro óptico provocan su giro.
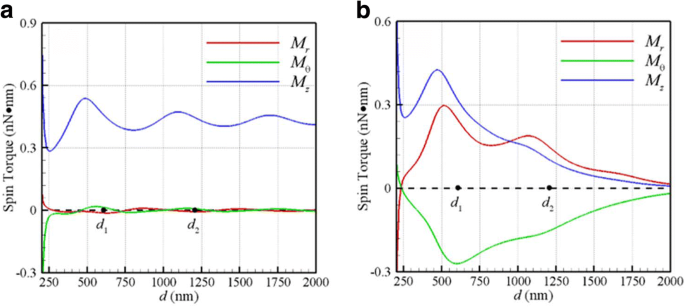
Pares de giro óptico ( M r , M θ , M z ) versus d en λ =800 nm para a onda plana y b Haz gaussiano con w 0 =500 nm en el plano focal
Además, se puede ajustar el iris del objeto de las pinzas ópticas para cambiar el tamaño del haz incidente, alterando así la apertura numérica y la cintura de un haz gaussiano. La figura 4a muestra el par orbital óptico F θ d / 2 en dos NP de Au acopladas de radio de 100 nm que giran en la primera órbita de equilibrio estable correspondiente ( d = d 1 ) frente a la cintura de un haz CP gaussiano de λ =800 nm. La primera distancia de equilibrio estable correspondiente d 1 también se representa en la Fig. 4a (barra de escala en el lado derecho), donde una onda plana puede tratarse como un caso especial de w 0 → ∞. El punto de inflexión de la cintura de un rayo gaussiano entre los pares orbitales positivo y negativo está a 1150 nm, correspondiente a F θ =0, como se muestra en la Fig. 4a. Cuanto más pequeña es la cintura de un rayo gaussiano, mayor es la magnitud del par orbital negativo. A medida que aumenta la cintura, el d 1 de un haz gaussiano se aproxima al valor (603 nm) de una onda plana ( w 0 → ∞). En particular, a medida que la cintura disminuye, las magnitudes de los pares de giro transversales ( M r , M θ ) en d 1 aumenta significativamente, mientras que el par de giro longitudinal M z disminuye, como se muestra en la Fig. 4b. Estos resultados ilustran que la cintura de un rayo gaussiano es el factor clave para inducir un par orbital longitudinal negativo y un par de giro transversal debido al grado de distorsión del campo EM.
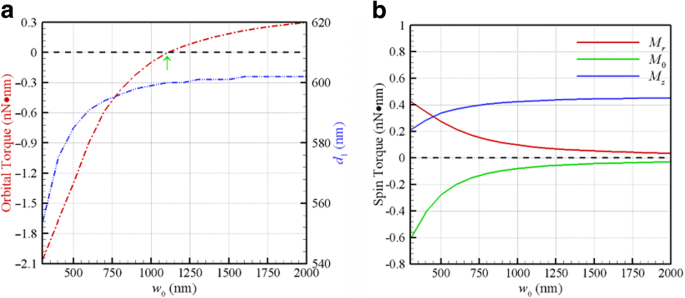
un El par orbital óptico y d 1 en la primera órbita de equilibrio estable frente a la cintura de un rayo gaussiano de λ =800 nm. El punto de inflexión de la cintura para producir un par orbital positivo o negativo es a 1150 nm. b Los pares de giro óptico frente a la cintura en d 1
El mecanismo de la rotación orbital negativa y el giro transversal de estos NP podría atribuirse al rizo del momento angular de giro del campo de luz, incluso sin la contribución del momento angular orbital del haz de luz [23]. A través de las actuaciones del par orbital longitudinal negativo y los pares de giro transversal sobre el dímero Au, se puede manifestar el SOC de fotones mejorado con plasmón. Además, las direcciones de la rotación orbital del dímero y el giro del NP individual dependen de la orientación de la luz incidente.
Conclusiones
Se estudiaron teóricamente las respuestas optomecánicas (fuerzas ópticas y pares) de un par de NP de Au irradiadas con luz CP. Nuestros resultados mostraron que las órbitas de equilibrio estable para su rotación (revolución) pueden inducirse para la interacción de largo alcance; las distancias entre partículas de equilibrio estable son casi los múltiplos enteros de la longitud de onda en el medio. La fuerza óptica azimutal provoca la rotación orbital de estos NP y el par de giro óptico induce su giro, en particular los componentes transversales. Este movimiento es similar al de las estrellas binarias de igual masa que se mueven en una órbita circular alrededor de su centro de masa común. Cuando la cintura de un rayo gaussiano es más pequeña que un punto de inflexión, la helicidad de la rotación orbital del dímero de Au ópticamente ligado es opuesta a la mano de la luz CP incidente. Además, el SOC longitudinal / transversal se vuelve significativo a medida que disminuye la cintura de un rayo gaussiano; por lo tanto, el giro transversal de los dos NP se vuelve más profundo. Para la interacción de corto alcance, la fuerza óptica provoca la atracción mutua. En consecuencia, los dos NP plasmónicos acoplados no solo giran sino que también giran con una trayectoria en espiral y eventualmente colisionarán. Además, el límite de la distancia entre partículas entre las interacciones de largo y corto alcance de dos NP acopladas se encuentra aproximadamente a media longitud de onda en el medio. Nuestros resultados demostraron que el orden de magnitud de la fuerza óptica es aproximadamente pN, que se puede comparar con las otras fuerzas (por ejemplo, fuerza ponderomotriz) para identificar la contribución al movimiento de NP. Nuestro hallazgo puede allanar el camino para las aplicaciones de SOC en NP que manipulan la luz para nanociencia y nanotecnología. Además, vale la pena estudiar la correlación entre el espín óptico y los pares orbitales en los dos NP y las densidades de espín y momento angular orbital del campo EM; el primero está definido por \ (\ operatorname {Im} \ left (\ overline {\ mathbf {E}} \ times \ mathbf {E} \ right) / 2 \ omega \) y el último se muestra en la Ref. [23]. Además, vale la pena investigar el SOC en el retorcido campo cercano de los metamateriales [40,41,42,43].
Abreviaturas
- CP:
-
Polarizado circularmente
- EM:
-
Electromagnético
- LH:
-
Zurdo
- LP:
-
Linealmente polarizado
- MMP:
-
Multipolar
- MP:
-
Micropartícula
- NP:
-
Nanopartícula
- SOC:
-
Acoplamiento de giro-órbita
Nanomateriales
- Comunicación de datos ópticos
- Fibra óptica
- Conceptos básicos y aplicaciones del sensor óptico
- Sensor de temperatura y luz Raspberry Pi
- Modulación de las propiedades de anisotropía óptica y electrónica de ML-GaS por campo eléctrico vertical
- Síntesis fácil y propiedades ópticas de nanocristales y nanovarillas de selenio pequeños
- Control de no linealidad dual de las propiedades de modo y dispersión en la guía de ondas plasmónica de grafeno-dieléctrico
- Ingeniería del proceso de recubrimiento por inmersión y optimización del rendimiento para dispositivos electrocrómicos de tres estados
- Estrategia de superenfoque de campo cuasi lejano dependiente de la polarización de las lentes plasmónicas basadas en nanorrestación
- Los científicos desarrollan un nuevo método para hacer que las pantallas sean más brillantes y eficientes
- Antenas ópticas multiplexadas



