Mejora del aislamiento óptico en chip mediante interacción espín-órbita de la paradoja de la moneda para un rendimiento magneto-óptico superior

Resumen

Diseñamos un aislamiento óptico integrado en chip simple compuesto por una guía de onda metal-aislante-metal y una cavidad de disco rellena con material magneto-óptico para mejorar el efecto magneto-óptico transversal mediante la interacción espín-órbita (SOI) de la paradoja de la moneda. Los resultados de simulación de las propiedades de transmisión no recíproca de esta estructura óptica muestran que se obtiene un aislamiento óptico integrado en chip de alto rendimiento. La relación de aislamiento máxima es superior a 60 dB con una pérdida de inserción correspondiente de aproximadamente 2 dB. El gran rendimiento del aislamiento óptico se atribuye al fuerte efecto magneto-óptico transversal, que se mejora mediante la SOI de la paradoja de la moneda. Además, la mejora del efecto magneto-óptico transversal a través de la SOI de la paradoja de la moneda es más sustancial para números de modo azimutal n más pequeños. Beneficiándose de esto, el efecto magneto-óptico transversal permanece fuerte en un amplio rango de longitudes de onda. Además, una cavidad más pequeña tiene un efecto magneto-óptico transversal más fuerte en el mismo rango de longitudes de onda. Nuestra investigación proporciona una nueva perspectiva para crear dispositivos magneto-ópticos altamente integrados.

Introducción

Los aislamientos ópticos basados en transmisión no recíproca son elementos fotónicos clave en telecomunicaciones ópticas y procesamiento de información óptica. Para lograr un aislamiento óptico más integrado, se han desarrollado muchos métodos, como el uso del efecto magneto-óptico [1,2,3,4,5], topología [6], efectos no lineales [7,8,9,10,11,12] y ruptura de simetría paridad-tiempo [13,14,15]. Entre estos, el efecto magneto-óptico sigue siendo un foco de investigación. Sin embargo, los dispositivos creados hasta ahora han sido típicamente de gran escala [2, 16] porque el efecto magneto-óptico es mayormente débil en estos casos.

El polaritón de plasmón de superficie (SPP) puede romper el límite de difracción [17, 18] y tiene un excelente potencial en óptica integrada [19,20,21], especialmente después de la mejora en el problema de las altas pérdidas de SPP [22]. El SPP tiene momento angular de espín transversal (TSAM) [23,24,25], que puede inducir un efecto magneto-óptico para realizar una transmisión no recíproca similar al momento angular de espín longitudinal (LSAM) de la luz [26,27,28]. Sin embargo, es difícil miniaturizar el aislamiento basado en el efecto magneto-óptico transversal de SPP debido al débil efecto magneto-óptico. Hay dos razones clave que resultan en el débil efecto magneto-óptico transversal de SPP: una es el pequeño coeficiente magneto-óptico de los materiales magneto-ópticos, y la otra es que el espín transversal de SPP no es circular, sino elíptico [26]. Actualmente, se han fabricado y aplicado a aislamientos ópticos una variedad de materiales magneto-ópticos con grandes coeficientes magneto-ópticos [4, 29,30,31,32]. Esto brinda esperanza para crear aislamientos ópticos miniaturizados con estructuras plasmónicas. Pero, por otro lado, el espín transversal elíptico de SPP sigue siendo el cuello de botella para la aplicación del efecto magneto-óptico transversal. El descubrimiento de nuevos métodos para mejorar el efecto magneto-óptico transversal sigue siendo deseado.

El espín y los momentos angulares orbitales (SAM y OAM) son dos componentes distintos de la luz. Estos pueden interactuar entre sí eficazmente, es decir, a través de la interacción espín-órbita (SOI). Se han descubierto muchos efectos ópticos esenciales y valiosos basados en la SOI de la luz, incluyendo el efecto Hall de espín, efecto Hall cuántico de espín, topología, etc. La paradoja de la moneda es un fenómeno natural fascinante, que muestra una SOI distintiva: la órbita circunferencial causa el cambio de rotación del espín. Así, la SOI de la paradoja de la moneda puede ser un nuevo mecanismo físico para regular el efecto magneto-óptico transversal de SPP.

Este trabajo informa el diseño de un aislamiento óptico integrado en chip simple compuesto por una guía de onda metal-aislante-metal (MIM) y una cavidad de disco rellena con un material magneto-óptico. En esta estructura de aislamiento óptico, se confirmó la mejora efectiva del efecto magneto-óptico transversal a través de la SOI de la paradoja de la moneda. Beneficiándose del efecto magneto-óptico transversal mejorado en la estructura del aislamiento óptico, los valles resonantes de transmisión hacia adelante y hacia atrás en los espectros de transmisión se separaron completamente entre sí cuando el parámetro magneto-óptico \(\varepsilon_{xy} \ge 0.04\). Se obtuvo un aislamiento óptico integrado en chip de alto rendimiento, para el cual la relación de aislamiento máxima (IR) fue mayor a 60 dB y la pérdida de inserción (IL) correspondiente fue de aproximadamente 2 dB. Debido a las propiedades únicas de la SOI de la paradoja de la moneda en la estructura del aislamiento óptico, la mejora del efecto magneto-óptico transversal es más sustancial para números de modo azimutal n más pequeños. El efecto magneto-óptico transversal permaneció fuerte en un amplio rango de longitudes de onda. Además, apareció un mayor efecto magneto-óptico transversal en una cavidad de disco más pequeña, lo que podría superar eficazmente el ensanchamiento de los valles resonantes inducido por la cavidad más pequeña. La estructura de fuerte efecto magneto-óptico transversal desarrollada aquí tiene un enorme potencial de aplicación en dispositivos magneto-ópticos altamente integrados en chip, aislamientos ópticos, interruptores magneto-ópticos, sensores magnéticos, etc.

Métodos

La Figura 1 muestra la ilustración esquemática de la estructura de aislamiento óptico propuesta compuesta por una guía de onda MIM y una cavidad de disco. El radio (R) de la cavidad de disco se estableció en 540 nm, el ancho de la guía de onda MIM d se estableció en 50 nm y la brecha entre la cavidad de disco y la guía de onda MIM g se estableció en 16,6 nm. El metal es plata, cuya permitividad relativa compleja dependiente de la frecuencia se caracteriza por el modelo de Drude:

$$\varepsilon_{m} (\omega ) = \varepsilon_{\infty } - \omega_{p}^{2} /\omega (\omega + i\gamma )$$ (1)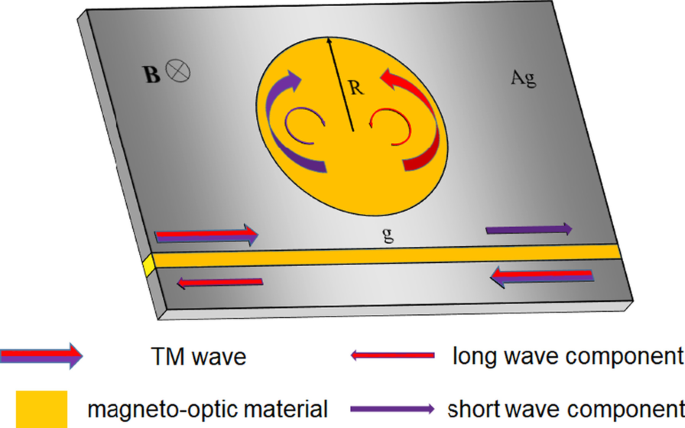

Ilustración esquemática de la estructura del aislamiento óptico compuesta por una guía de onda MIM y una cavidad de disco. La guía de onda MIM y la cavidad de disco están llenas de material magneto-óptico y permanecen bajo un campo magnético estático

Aquí, \(\varepsilon_{\infty }\) es la constante dieléctrica a frecuencia infinita, γ es la frecuencia de colisión de electrones, \(\omega_{p}\) es la frecuencia de plasma en masa, y ω es la frecuencia angular de la luz incidente. Los parámetros introducidos en la Ec. (1) fueron \(\varepsilon_{\infty }\) = 3,7, \(\omega_{p}\) = 9,1 eV, γ = 0,018 eV [33]. Para excitar los SPPs, la luz de entrada se estableció como onda plana magnética transversal (TM).

La cavidad de disco y la guía de onda MIM fueron llenadas con material magneto-óptico, y se aplica un campo magnético estático transversal. El efecto del campo magnético estático en los materiales magneto-ópticos se refleja en gran medida en el tensor dieléctrico de los materiales. Para materiales magneto-ópticos anisotrópicos, un campo magnético estático B puede aplicarse en la dirección z, donde el tensor dieléctrico puede expresarse como:

$${{\varvec{\upvarepsilon}}} = \left( {\begin{array}{*{20}c} {\varepsilon_{xx} } & { - i\varepsilon_{xy} } & 0 \\ {i\varepsilon_{xy} } & {\varepsilon_{yy} } & 0 \\ 0 & 0 & {\varepsilon_{zz} } \\ \end{array} } \right)$$ (2)

El material magneto-óptico se establece como granate de hierro de itrio dopado con bismuto (Bi:YIG). El granate pertenece a la estructura cristalina cúbica y es isotrópico, por lo que los elementos diagonales de su tensor dieléctrico son idénticos, es decir, \(\varepsilon_{xx} = \varepsilon_{yy} = \varepsilon_{zz} = \varepsilon_{0} = n^{2}\). La constante dieléctrica \(\varepsilon_{0}\) del elemento diagonal se establece en 4,84, el índice de refracción típico de YIG cerca de la longitud de onda de 1,5 µm [34]. Recientemente, experimentos han demostrado que \(\varepsilon_{xy}\) puede ser mayor a 0,3 [35] y el \(\varepsilon_{xy}\) predicho teóricamente [36] es mucho mayor que el obtenido experimentalmente. En este trabajo, el valor de \(\varepsilon_{xy}\) se estableció de 0 a 0,3. Este dispositivo puede fabricarse mediante grabado químico asistido por metal [37, 38] y litografía de haz de electrones (EBL).

Se empleó el software comercial COMSOL Multiphysics para la construcción del modelo y cálculos de simulación basados en el método de elementos finitos (FEM). Para comodidad de la investigación, toda la estructura fue bidimensional. El vector de Poynting S que pasa se integró en los extremos de entrada y salida para obtener la energía de entrada \(P_{\text{in}}\) y la energía de salida \(P_{{{\text{out}}}}\), \(P_{{{\text{in}}}} = \int {{\mathbf{S}}_{1} \bullet {\text{d}}{\varvec{s}}_{1} }\), \(P_{{{\text{out}}}} = \int {{\mathbf{S}}_{2} \bullet {\text{d}}{\varvec{s}}_{2} }\) y la transmitancia \(T = 10{*}\lg \left( {P_{{{\text{out}}}} /P_{{{\text{in}}}} } \right)\) dB. IL es la tasa de transmisión hacia atrás en la longitud de onda de aislamiento hacia adelante y se calcula usando los datos de transmitancia obtenidos en la simulación. La entrada de luz se dio desde la izquierda de la guía de onda MIM, y su salida desde la derecha se etiqueta como 'hacia adelante' en este artículo. Contrariamente, la entrada de luz desde la derecha de la guía de onda MIM resultó en la salida desde la izquierda, y se llama 'hacia atrás'.

Resultados y Discusión

Como se muestra en la Fig. 1, la cavidad de disco soporta una fascinante SOI de la paradoja de la moneda. Por ejemplo, para el modo TM_(0,n), el espín transversal y la rotación orbital de SPP se encuentran en la misma dirección. El SPP viaja alrededor de la cavidad de disco una vuelta, y el vector de campo eléctrico rota n + 1 vueltas. La órbita circular causa la vuelta extra. Este efecto es similar a la paradoja de la moneda y forma una SOI única. La SOI de la paradoja de la moneda es más significativa para n más pequeño. Los resultados de simulación confirman que la SOI de la paradoja de la moneda puede mejorar el efecto magneto-óptico transversal eficazmente.

La Figura 2 muestra los espectros de transmisión de las estructuras de aislamiento óptico para diferentes \(\varepsilon_{xy}\). Para el caso de \(\varepsilon_{xy} = 0\), los espectros de transmisión hacia adelante y hacia atrás se superponen, el espectro de transmisión se muestra como línea negra sólida. La línea roja sólida muestra el espectro de transmisión para el caso de \(\varepsilon_{xy} = 0.3\) hacia adelante, línea roja punteada para el caso de \(\varepsilon_{xy} = 0.3\) hacia atrás. Como se muestra en la Fig. 2, hay cuatro valles de transmisión prominentes en cada espectro de transmisión. Para el caso de \(\varepsilon_{xy} = 0\), cuatro valles de transmisión se ubican en 1936,0 nm, 1550,2 nm, 1460,0 nm y 1302,5 nm, respectivamente. Para el modelado bidimensional de elementos finitos, las resonancias de la cavidad de disco se caracterizan por dos enteros (m_i, n_i) que cuentan los antinodos radiales y azimutales. Según las distribuciones de intensidad del componente z del campo magnético mostradas en los recuadros, los cuatro valles de transmisión inducidos por modos resonantes son: TM_0,3, TM_0,4, TM_1,1 y TM_0,5. En este artículo, nos centramos principalmente en el efecto magneto-óptico transversal de SPP, y por lo tanto, los modos resonantes: TM_0,3, TM_0,4 y TM_0,5 fueron investigados en detalle.

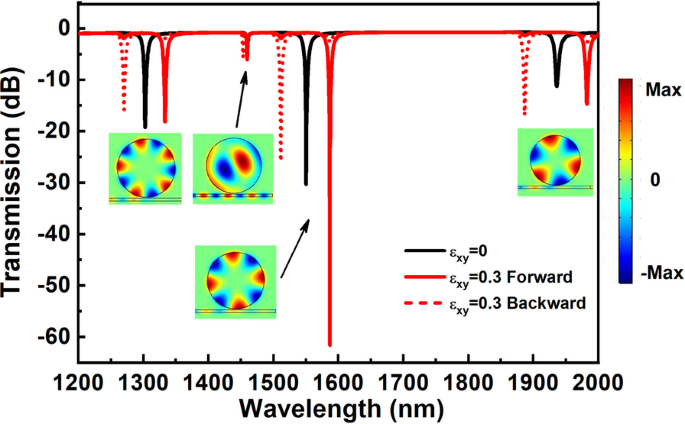
Espectros de transmisión totales de las estructuras de aislamiento óptico para diferentes \(\varepsilon_{xy}\). La línea negra sólida muestra el espectro de transmisión para \(\varepsilon_{xy} = 0\), línea roja sólida para \(\varepsilon_{xy} = 0.3\) hacia adelante y la línea roja punteada para \(\varepsilon_{xy} = 0.3\) hacia atrás. Los recuadros debajo de los espectros de transmisión son las distribuciones de intensidad del componente z del campo magnético, correspondientes al caso de \(\varepsilon_{xy} = 0\)

Inicialmente, se estudió el rendimiento de aislamiento de la estructura de aislamiento óptico del modo resonante TM_0,4. La Figura 3a, b muestran los espectros de transmisión de las estructuras de aislamiento óptico del modo resonante TM_0,4 con diferentes \(\varepsilon_{xy}\). Sin ningún campo magnético, el valle de transmisión se ubica en aproximadamente 1550,2 nm. Al aplicar el campo magnético, el valle transmitido tiene un desplazamiento al rojo a medida que el SPP viaja hacia adelante y un desplazamiento al azul casi simétrico a medida que el SPP viaja hacia atrás. Así, se observó la división de los valles resonantes hacia adelante y hacia atrás. Con el aumento en el valor del parámetro magneto-óptico \(\varepsilon_{xy}\), la longitud de onda se desplazó y la división aumentó. La Figura 3c muestra la curva de la división de los valles resonantes hacia adelante y hacia atrás variando con el parámetro magneto-óptico \(\varepsilon_{xy}\). Como se muestra en la Fig. 3c, la división está prácticamente relacionada positivamente con el parámetro magneto-óptico \(\varepsilon_{xy}\). La Figura 3d muestra la IR y la IL de la estructura de aislamiento óptico del modo resonante TM_0,4 para diferentes \(\varepsilon_{xy}\). Con el aumento en el valor de \(\varepsilon_{xy}\), tanto la IL hacia adelante como hacia atrás disminuyeron. Además, cuando \(\varepsilon_{xy} \ge 0.05\), la IL fue tan pequeña como aproximadamente 2 dB y permaneció estable. Esto significa que los valles resonantes hacia adelante y hacia atrás estaban completamente separados entre sí. La IR hacia adelante y hacia atrás exhibieron diferentes curvas de cambio a medida que \(\varepsilon_{xy}\) aumentaba. Como se muestra en la Fig. 3d, obtenemos la IR máxima mayor a 60 dB con una IL correspondiente de aproximadamente 2 dB. La IR fue determinada por la profundidad del valle de transmisión. Depende de la distancia de acoplamiento entre la guía de onda MIM y la cavidad de disco. Así, la IR puede ajustarse finamente cambiando la brecha entre la guía de onda MIM y la cavidad de disco, g. Los resultados relevantes muestran que el gran efecto magneto-óptico existe en la estructura de aislamiento óptico presentada aquí, y como resultado, se obtiene un aislamiento óptico integrado en chip de alto rendimiento.

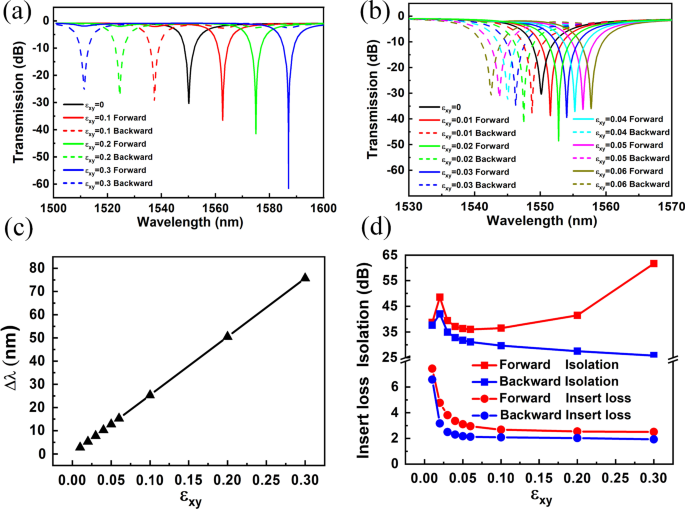
Espectros de transmisión, división de longitud de onda, IR e IL en modo TM_0,4. a, b Espectros de transmisión de luz de diferentes direcciones de propagación acopladas a la cavidad de disco con diferentes \(\varepsilon_{xy}\). c, d Gráficos lineales de división de longitud de onda, IR e IL en función de \(\varepsilon_{xy}\)

La mejora del efecto magneto-óptico transversal por la SOI de la paradoja de la moneda será más significativa para números de modo azimutal n más pequeños. Los resultados de simulación pueden usarse para probar esta ley. Como se muestra en la Fig. 2, para los casos de TM_0,5, TM_0,4 y TM_0,3, la división \(\Delta \lambda\) aumentó con la disminución del número de modo azimutal n. Para comparar con precisión la intensidad del efecto magneto-óptico transversal de diferentes modos, se trazan gráficos de línea de la relación \(\Delta \lambda /\lambda\) variando con \(\varepsilon_{xy}\) para diferentes modos en la Fig. 4. Como se muestra en la Fig. 4, para tres modos diferentes, la relación \(\Delta \lambda /\lambda\) solo tiene un ligero cambio. Además, como se muestra en los recuadros, las relaciones \(\Delta \lambda /\lambda\) de TM_0,5 y TM_0,4 son casi las mismas y la de TM_0,3 es la más grande. Estos resultados de simulación son contrarios a la teoría reportada en Ref. [26]. Para los casos de TM_0,5, TM_0,4 y TM_0,3, la longitud de onda de resonancia aumentó con la disminución del número de modo azimutal n, lo cual se muestra claramente en la Fig. 2. A medida que la longitud de onda aumentó, el valor absoluto de la permitividad dieléctrica del metal \(\varepsilon_{M}\) aumentó rápidamente, resultando en una disminución de \(\beta_{SPP}\). Según la teoría en Ref. [26], se esperaba que el efecto magneto-óptico transversal se debilitara, y la relación \(\Delta \lambda /\lambda\) fuera menor. Por lo tanto, los resultados de simulación presentes son contrarios a la teoría en Ref. [26]. La mejora en el efecto magneto-óptico transversal por la SOI de la paradoja de la moneda puede resolver esta contradicción entre los resultados de simulación y la teoría en Ref. [26]. Como se mencionó anteriormente, la SOI de la paradoja de la moneda es más significativa para números de modo azimutal n más pequeños. Así, la mejora en el efecto magneto-óptico transversal por la SOI de la paradoja de la moneda puede cancelar o incluso superar el debilitamiento desencadenado por el aumento de la longitud de onda. Además, se puede concluir que el efecto magneto-óptico transversal anormalmente grande mencionado en este trabajo es causado por la SOI de la paradoja de la moneda y permanece fuerte en un amplio rango de longitudes de onda.

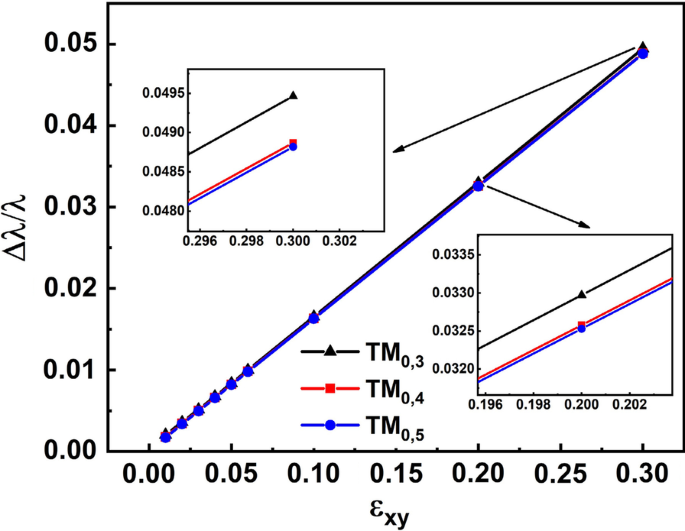
Gráfico de línea de la relación \(\Delta \lambda /\lambda\) variando con \(\varepsilon_{xy}\) para diferentes modos. Los recuadros son la vista parcialmente ampliada de los puntos de datos cuando \(\varepsilon_{xy} = 0.2\) y \(\varepsilon_{xy} = 0.3\)

Para números de modo azimutal n más pequeños, la mejora del efecto magneto-óptico transversal por la SOI de la paradoja de la moneda es más significativa. Por lo tanto, una cavidad más pequeña tendrá un mayor efecto magneto-óptico transversal en el mismo rango de longitudes de onda, es decir, una mayor división de longitud de onda. Para confirmar esta conclusión, el radio de la cavidad de disco R se estableció en un valor menor, 421 nm. El espectro de transmisión de la cavidad más pequeña R = 421 nm se muestra en la Fig. 5a, y se compara con el de la cavidad más grande R = 540 nm. Se puede ver que TM_0,3 para la cavidad más pequeña R = 421 nm y TM_0,4 para la cavidad más grande R = 540 nm están ambos ubicados en aproximadamente 1550 nm. El gráfico lineal de la división de longitud de onda cambiando con \(\varepsilon_{xy}\) para diferentes radios de cavidad de disco se traza en la Fig. 5b. Es obvio que la división de longitud de onda de la cavidad más pequeña es mayor que la de la cavidad más grande, lo que concuerda con nuestras expectativas. Además, la mejora del efecto magneto-óptico transversal por la SOI de la paradoja de la moneda se prueba nuevamente.

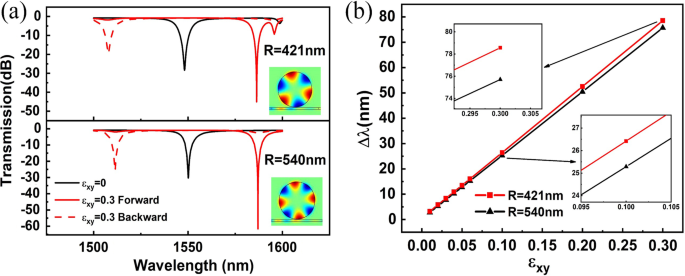
Espectros de transmisión y división de longitud de onda de la cavidad de disco con diferentes radios. a Los espectros de transmisión de luz de diferentes direcciones de propagación son acoplados a una cavidad de disco con diferentes radios. Los recuadros corresponden a la distribución de intensidad del componente z del campo magnético cuando \(\varepsilon_{xy} = 0\). b Gráfico lineal de división de longitud de onda para cavidad de disco con diferentes radios

Es bien conocido que con la disminución del radio de la cavidad de disco, el ancho a media altura (FWHM) de la línea espectral aumentará. Un FWHM mayor ha sido el principal obstáculo insuperable que dificulta la aplicación de cavidades con volúmenes de modelo más pequeños. El cambio en FWHM inducido por el cambio de \(\varepsilon_{xy}\) puede ignorarse. Con el radio de la cavidad de disco disminuyendo de 540 a 421 nm, el FWHM aumentó de aproximadamente 9,914 nm a aproximadamente 10,811 nm. Con la disminución del radio de la cavidad de disco, el FWHM aumentó en aproximadamente 0,897 nm. Esta expansión lineal puede ser compensada eficazmente por la división aumentada. Por ejemplo, cuando \(\varepsilon_{xy} = 0.1\), el aumento en la división de longitud de onda fue de aproximadamente 1,130 nm. Cuando \(\varepsilon_{xy} = 0.3\), el aumento en la división de longitud de onda fue de aproximadamente 2,850 nm, mucho mayor que 0,897 nm. Por lo tanto, la estructura de aislamiento óptico presentada aquí tiene un mayor potencial de aplicación en un tamaño más pequeño y es más propicia para un mayor grado de integración óptica.

Conclusiones

En resumen, se diseñó un aislamiento óptico integrado en chip simple compuesto por una guía de onda MIM y una cavidad de disco llena con material magneto-óptico. En esta estructura de aislamiento óptico, existe una novedosa SOI de la paradoja de la moneda, que mejora el efecto magneto-óptico transversal eficazmente. Además, la mejora es más significativa para números de modo azimutal n más pequeños. Basado en el efecto magneto-óptico transversal mejorado, se obtuvo un aislamiento óptico integrado en chip de alto rendimiento. La IR máxima se encontró mayor a 60 dB con IL de aproximadamente 2 dB. El efecto magneto-óptico transversal permanece fuerte en un amplio rango de longitudes de onda. Además, se verifica el mayor efecto magneto-óptico transversal de las cavidades más pequeñas, lo que puede superar eficazmente el ensanchamiento de los valles resonantes inducido por la cavidad más pequeña.

Disponibilidad de datos y materiales

Todos los datos que respaldan las conclusiones de este artículo están incluidos dentro del artículo.

Abreviaturas

SPP:

Polaritón de plasmón de superficie

TSAM:

Momento angular de espín transversal

LSAM:

Momento angular de espín longitudinal

SAM:

Momentos angulares de espín

OAM:

Momentos angulares orbitales

SOI:

Interacción espín-órbita

MIM:

Metal-Aislante-Metal

IR:

Relación de aislamiento

IL:

Pérdida de inserción

TM:

Magnético transversal

Bi:YIG:

Granate de hierro de itrio dopado con bismuto

FEM:

Método de elementos finitos

FWHM:

Ancho a media altura

EBL:

Litografía de haz de electrones

Oxinitruro de boro-carbono (BCNO): un fotocatalizador libre de metal innovador para producción de hidrógeno solar y degradación de colorantes Nanopartículas de oro: Avanzando aplicaciones diagnósticas y terapéuticas en medicina – Una revisión exhaustiva