Principios de ingeniería de confiabilidad para el ingeniero de planta

Cada vez más, los gerentes e ingenieros responsables de la fabricación y otras actividades industriales están incorporando un enfoque de confiabilidad en sus planes e iniciativas estratégicos y tácticos. Esta tendencia está afectando a numerosas áreas funcionales, incluido el diseño y la adquisición de máquinas / sistemas, las operaciones y el mantenimiento de la planta.

Con sus orígenes en la industria de la aviación, la ingeniería de confiabilidad, como disciplina, se ha centrado históricamente principalmente en asegurar la confiabilidad del producto. Cada vez más, estos métodos se emplean para asegurar la confiabilidad de la producción de las plantas y equipos de fabricación, a menudo como un facilitador para la manufactura esbelta. Este artículo proporciona una introducción a los métodos más relevantes y prácticos para la ingeniería de confiabilidad de plantas, que incluyen:

• Cálculos básicos de confiabilidad para la tasa de fallas, MTBF, disponibilidad, etc.
• Una introducción a la distribución exponencial, la piedra angular de los métodos de confiabilidad.
• Identificar las dependencias del tiempo de falla utilizando el versátil sistema Weibull.
• Desarrollar un sistema de recopilación de datos de campo eficaz.

Historial de ingeniería de confiabilidad

Los orígenes del campo de la ingeniería de confiabilidad, al menos su demanda, se remontan al punto en que el hombre comenzó a depender de las máquinas para su sustento. La Noria, por ejemplo, es una bomba antigua que se cree que es la primera máquina sofisticada del mundo. Utilizando energía hidráulica del flujo de un río o arroyo, Noria utilizó baldes para transferir agua a abrevaderos, viaductos y otros dispositivos de distribución para regar los campos y proporcionar agua a las comunidades.

Si la comunidad de Noria fracasaba, las personas que dependían de ella para su suministro de alimentos estaban en riesgo. La supervivencia siempre ha sido una gran fuente de motivación para la confiabilidad y la confiabilidad.

Si bien los orígenes de su demanda son antiguos, la ingeniería de confiabilidad como disciplina técnica realmente floreció junto con el crecimiento de la aviación comercial después de la Segunda Guerra Mundial. Rápidamente se hizo evidente para los gerentes de las empresas de la industria de la aviación que los accidentes son perjudiciales para los negocios. Karen Bernowski, editora de Quality Progress , revelada en una de sus editoriales, la investigación sobre el valor mediático de la muerte por diversos medios, que fue realizada por el profesor de estadística del MIT Arnold Barnett y reportada en 1994.

Barnett evaluó el número de artículos noticiosos de primera plana del New York Times por cada 1.000 muertes por diversos medios. Encontró que las muertes relacionadas con el cáncer produjeron 0,02 artículos de primera plana por cada 1.000 muertes, los homicidios produjeron 1,7 por cada 1.000 muertes, el sida produjo 2,3 por cada 1.000 muertes y los accidentes relacionados con la aviación produjeron la friolera de 138,2 artículos por cada 1.000 muertes.

El costo y la naturaleza de alto perfil de los accidentes relacionados con la aviación ayudaron a motivar a la industria de la aviación a participar fuertemente en el desarrollo de la disciplina de ingeniería de confiabilidad. Asimismo, debido a la naturaleza crítica del equipo militar en defensa, las técnicas de ingeniería de confiabilidad se han empleado durante mucho tiempo para asegurar la preparación operativa. Muchos de nuestros estándares en el campo de la ingeniería de confiabilidad son estándares MIL o tienen su origen en actividades militares.

¿Qué es la ingeniería de confiabilidad?

La ingeniería de confiabilidad se ocupa de la longevidad y confiabilidad de piezas, productos y sistemas. Más conmovedor, se trata de controlar el riesgo. La ingeniería de confiabilidad incorpora una amplia variedad de técnicas analíticas diseñadas para ayudar a los ingenieros a comprender los modos y patrones de falla de estas piezas, productos y sistemas. Tradicionalmente, el campo de la ingeniería de confiabilidad se ha centrado en la confiabilidad del producto y la garantía de confiabilidad.

En los últimos años, las organizaciones que implementan máquinas y otros activos físicos en entornos de producción han comenzado a implementar varios principios de ingeniería de confiabilidad con el propósito de garantizar la confiabilidad y confiabilidad de la producción.

Cada vez más, las organizaciones de producción implementan técnicas de ingeniería de confiabilidad como el mantenimiento centrado en la confiabilidad (RCM), que incluyen modos de falla y análisis de efectos (y criticidad) (FMEA, FMECA), análisis de causa raíz (RCA), mantenimiento basado en condiciones, esquemas mejorados de planificación del trabajo, Estas mismas organizaciones están comenzando a adoptar estrategias de adquisición y diseño basadas en costos de ciclo de vida, esquemas de gestión de cambios y otras herramientas y técnicas avanzadas para controlar las causas fundamentales de la mala confiabilidad.

Sin embargo, la adopción de los aspectos más cuantitativos de la ingeniería de confiabilidad por parte de la comunidad de aseguramiento de la confiabilidad de la producción ha sido lenta. Esto se debe en parte a la complejidad percibida de las técnicas y en parte a la dificultad para obtener datos útiles.

Los aspectos cuantitativos de la ingeniería de confiabilidad pueden, en la superficie, parecer complicados y abrumadores. Sin embargo, en realidad, una comprensión relativamente básica de los métodos más fundamentales y ampliamente aplicables puede permitir al ingeniero de confiabilidad de la planta obtener una comprensión mucho más clara sobre dónde están ocurriendo los problemas, su naturaleza y su impacto en el proceso de producción, al menos en el nivel cuantitativo. sentido.

Si se usan correctamente, las herramientas y los métodos de ingeniería de confiabilidad cuantitativa permiten que la ingeniería de confiabilidad de la planta aplique de manera más efectiva los marcos proporcionados por RCM, RCA, etc., al eliminar algunas de las conjeturas involucradas con su aplicación. Sin embargo, los ingenieros deben ser particularmente inteligentes en la aplicación de los métodos.

¿Por qué? El contexto operativo y el entorno de un proceso de producción incorporan más variables que el mundo unidimensional de la garantía de fiabilidad del producto. Esto se debe a la influencia combinada de la ingeniería de diseño, las adquisiciones, la producción / operaciones, el mantenimiento, etc., y la dificultad de crear pruebas y experimentos efectivos para modelar los aspectos multidimensionales de un entorno de producción típico.

A pesar de la mayor dificultad para aplicar métodos de confiabilidad cuantitativa en el entorno de producción, vale la pena obtener una comprensión sólida de las herramientas y aplicarlas cuando sea apropiado. Los datos cuantitativos ayudan a definir la naturaleza y la magnitud de un problema / oportunidad, lo que proporciona una visión de la confiabilidad en su aplicación de otras herramientas de ingeniería de confiabilidad.

Este artículo proporcionará una introducción a los métodos de ingeniería de confiabilidad más básicos que son aplicables al ingeniero de planta que está interesado en la garantía de confiabilidad de la producción. Presupone una comprensión básica de álgebra, teoría de la probabilidad y estadística univariante basada en la distribución gaussiana (normal) (por ejemplo, medida de tendencia central, medidas de dispersión y variabilidad, intervalos de confianza, etc.).

Debe quedar claro que este documento es una breve introducción a los métodos de confiabilidad. De ninguna manera es un estudio completo de los métodos de ingeniería de confiabilidad, ni es de ninguna manera nuevo o poco convencional. Los métodos descritos en este documento son utilizados habitualmente por ingenieros de confiabilidad y son conceptos básicos de conocimiento para aquellos que buscan la certificación profesional de la Sociedad Estadounidense de Calidad (ASQ) como ingeniero de confiabilidad (CRE).

En la bibliografía de este artículo se enumeran varios libros sobre ingeniería de confiabilidad. El autor de este artículo ha encontrado Métodos de confiabilidad para ingenieros por K.S. Krishnamoorthi y Estadísticas de confiabilidad por Robert Dovich para ser referencias particularmente útiles y fáciles de usar sobre el tema de los métodos de ingeniería de confiabilidad. Ambos son publicados por ASQ Press.

Antes de discutir los métodos, debe familiarizarse con la nomenclatura de ingeniería de confiabilidad. Para mayor comodidad, en el apéndice de este artículo se proporciona una lista muy abreviada de términos y definiciones clave. Para obtener una definición más exhaustiva de los términos y la nomenclatura de confiabilidad, consulte MIL-STD-721 y otras normas relacionadas. Las definiciones contenidas en el apéndice son de MIL-STD-721.

Conceptos matemáticos básicos en ingeniería de confiabilidad

Muchos conceptos matemáticos se aplican a la ingeniería de confiabilidad, particularmente en las áreas de probabilidad y estadística. Asimismo, muchas distribuciones matemáticas se pueden utilizar para diversos fines, incluida la distribución gaussiana (normal), la distribución log-normal, la distribución de Rayleigh, la distribución exponencial, la distribución de Weibull y muchas otras.

Para el propósito de esta breve introducción, limitaremos nuestra discusión a la distribución exponencial y la distribución de Weibull, las dos más ampliamente aplicadas a la ingeniería de confiabilidad. En aras de la brevedad y la simplicidad, se han excluido conceptos matemáticos importantes como la bondad de ajuste de la distribución y los intervalos de confianza.

Tasa de fallas y tiempo medio entre / hasta fallas (MTBF / MTTF)

El propósito de las mediciones cuantitativas de confiabilidad es definir la tasa de falla en relación con el tiempo y modelar esa tasa de falla en una distribución matemática con el propósito de comprender los aspectos cuantitativos de la falla. El bloque de construcción más básico es la tasa de falla, que se estima utilizando la siguiente ecuación:

Donde:
λ =Tasa de falla (a veces denominada tasa de riesgo)
T =Tiempo total de funcionamiento / ciclos / millas / etc. durante un período de investigación para artículos fallidos y no fallidos.
r =El número total de fallas ocurridas durante el período de investigación.

Por ejemplo, si cinco motores eléctricos funcionan durante un tiempo total colectivo de 50 años con cinco fallas funcionales durante el período, la tasa de fallas es de 0.1 fallas por año.

Otro concepto muy básico es el tiempo medio entre / hasta el fallo (MTBF / MTTF). La única diferencia entre MTBF y MTTF es que empleamos MTBF cuando nos referimos a elementos que se reparan cuando fallan. Para los artículos que simplemente se desechan y reemplazan, usamos el término MTTF. Los cálculos son los mismos.

El cálculo básico para estimar el tiempo medio entre fallas (MTBF) y el tiempo medio hasta la falla (MTTF), ambas medidas de tendencia central, es simplemente el recíproco de la función de tasa de fallas. Se calcula utilizando la siguiente ecuación.

Donde:
θ =Tiempo medio entre / hasta la falla
T =Tiempo total de funcionamiento / ciclos / millas / etc. durante un período de investigación para artículos fallidos y no fallidos.
r =El número total de fallas ocurridas durante el período de investigación.

El MTBF para nuestro ejemplo de motor eléctrico industrial es de 10 años, que es el recíproco de la tasa de falla de los motores. Por cierto, estimaríamos el MTBF para motores eléctricos que se reconstruyen en caso de falla. Para motores más pequeños que se consideran desechables, indicaríamos la medida de tendencia central como MTTF.

La tasa de fallas es un componente básico de muchos cálculos de confiabilidad más complejos. Dependiendo del diseño mecánico / eléctrico, el contexto operativo, el entorno y / o la efectividad del mantenimiento, la tasa de falla de una máquina en función del tiempo puede disminuir, permanecer constante, aumentar linealmente o aumentar geométricamente (Figura 1). La importancia de la tasa de fallas frente al tiempo se discutirá con más detalle más adelante.

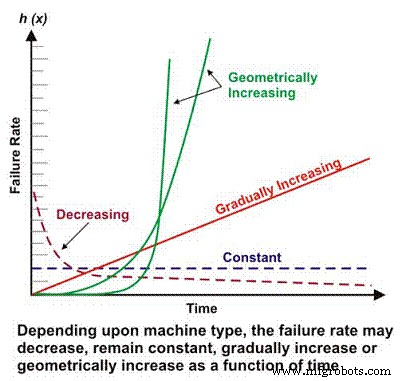
Figura 1. Diferentes tasas de fallas frente a escenarios de tiempo

La curva de la "bañera"

Los individuos que solo han recibido entrenamiento básico en probabilidad y estadística probablemente estén más familiarizados con la distribución normal o gaussiana, que está asociada con la conocida curva de densidad de probabilidad en forma de campana. La distribución gaussiana es generalmente aplicable a conjuntos de datos donde las dos medidas más comunes de tendencia central, media y mediana, son aproximadamente iguales.

Sorprendentemente, a pesar de la versatilidad de la distribución gaussiana en el modelado de probabilidades de fenómenos que van desde las puntuaciones de las pruebas estandarizadas hasta el peso al nacer de los bebés, no es la distribución dominante empleada en la ingeniería de confiabilidad. La distribución gaussiana tiene su lugar en la evaluación de las características de falla de las máquinas con un modo de falla dominante, pero la distribución principal empleada en la ingeniería de confiabilidad es la distribución exponencial.

Al evaluar la confiabilidad y las características de falla de una máquina, debemos comenzar con la tan difamada curva de "bañera", que refleja la tasa de falla en función del tiempo (Figura 2). En concepto, la curva de la bañera demuestra efectivamente las tres características básicas de la tasa de falla de una máquina:decreciente, constante o creciente. Lamentablemente, la curva de la bañera ha sido duramente criticada en la literatura de ingeniería de mantenimiento porque no logra modelar de manera efectiva la tasa de falla característica para la mayoría de las máquinas en una planta industrial, lo que generalmente es cierto a nivel macro.

La mayoría de las máquinas pasan sus vidas en las primeras etapas de la vida o en la mortalidad infantil y / o en las regiones de tasa de falla constante de la curva de la bañera. Rara vez vemos fallas sistémicas basadas en el tiempo en las máquinas industriales. A pesar de sus limitaciones para modelar las tasas de falla de las máquinas industriales típicas, la curva de la bañera es una herramienta útil para explicar los conceptos básicos de la ingeniería de confiabilidad.

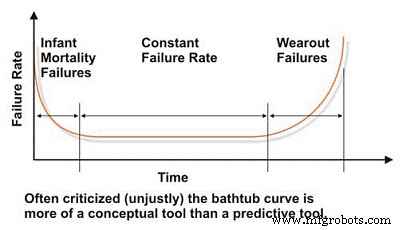
Figura 2. La tan difamada curva de la 'bañera'

El cuerpo humano es un excelente ejemplo de un sistema que sigue la curva de la bañera. Las personas, y otras especies orgánicas para el caso, tienden a sufrir una alta tasa de fallas (mortalidad) durante sus primeros años de vida, particularmente los primeros años, pero la tasa disminuye a medida que el niño crece. Suponiendo que una persona llega a la pubertad y sobrevive a su adolescencia, su tasa de mortalidad se vuelve bastante constante y permanece allí hasta que las enfermedades dependientes de la edad (tiempo) comienzan a aumentar la tasa de mortalidad (desgaste).

Numerosas influencias afectan las tasas de mortalidad, incluida la atención prenatal y la nutrición de la madre, la calidad y disponibilidad de la atención médica, el medio ambiente y la nutrición, las opciones de estilo de vida y, por supuesto, la predisposición genética. Estos factores pueden compararse metafóricamente con factores que influyen en la vida útil de la máquina. El diseño y la obtención son análogos a la predisposición genética; la instalación y puesta en servicio es análoga a la atención prenatal y la nutrición de la madre; y las opciones de estilo de vida y la disponibilidad de atención médica son análogas a la efectividad del mantenimiento y el control proactivo de las condiciones operativas.

La distribución exponencial

La distribución exponencial, la fórmula de predicción de confiabilidad más básica y ampliamente utilizada, modela máquinas con la tasa de falla constante, o la sección plana de la curva de la bañera. La mayoría de las máquinas industriales pasan la mayor parte de su vida con una tasa de fallas constante, por lo que es de amplia aplicación. A continuación se muestra la ecuación básica para estimar la confiabilidad de una máquina que sigue la distribución exponencial, donde la tasa de falla es constante en función del tiempo.

Donde:
R (t) =Estimación de confiabilidad para un período de tiempo, ciclos, millas, etc. (t).
e =Base de los logaritmos naturales (2.718281828)
λ =Tasa de falla (1 / MTBF, o 1 / MTTF)

En nuestro ejemplo de motor eléctrico, si asume una tasa de falla constante, la probabilidad de hacer funcionar un motor durante seis años sin falla, o la confiabilidad proyectada, es del 55 por ciento. Esto se calcula de la siguiente manera:
R (6) =2.718281828- (0.1 * 6)
R (6) =0.5488 =~ 55%

En otras palabras, después de seis años, es probable que falle aproximadamente el 45% de la población de motores idénticos que operan en una aplicación idéntica. Vale la pena reiterar en este punto que estos cálculos proyectan la probabilidad para una población. Cualquier individuo de la población podría fallar el primer día de operación, mientras que otro individuo podría durar 30 años. Esa es la naturaleza de las proyecciones probabilísticas de confiabilidad.

Una característica de la distribución exponencial es que el MTBF se produce en el punto en el que la fiabilidad calculada es del 36,78%, o en el punto en el que el 63,22% de las máquinas ya han fallado. En nuestro ejemplo de motor, después de 10 años, se puede esperar que el 63,22% de los motores de una población de motores idénticos que funcionan en aplicaciones idénticas fallen. En otras palabras, la tasa de supervivencia es del 36,78% de la población.

A menudo hablamos de vida proyectada de los rodamientos como vida L10. Este es el momento en el que se espera que falle el 10% de una población de rodamientos (tasa de supervivencia del 90%). En realidad, solo una fracción de los cojinetes sobrevive hasta el punto L10. Hemos llegado a aceptar eso como la vida objetiva para un rodamiento cuando quizás deberíamos fijar nuestra mirada en el punto L63.22, lo que indica que nuestros rodamientos duran, en promedio, al MTBF proyectado, asumiendo, por supuesto, que los rodamientos sigue la distribución exponencial. Discutiremos ese tema más adelante en la sección de análisis de Weibull del artículo.

La función de densidad de probabilidad (pdf), o distribución de vida, es una ecuación matemática que se aproxima a la distribución de frecuencia de falla. Es el pdf, o distribución de frecuencia de vida, lo que produce la conocida curva en forma de campana en la distribución gaussiana o normal. A continuación se muestra el pdf de la distribución exponencial.

Donde:
pdf (t) =Distribución de frecuencia de vida durante un tiempo determinado (t)
e =Base de los logaritmos naturales (2.718281828)
λ =Tasa de falla (1 / MTBF, o 1 / MTTF)

En nuestro ejemplo de motor eléctrico, la probabilidad real de falla a los tres años se calcula de la siguiente manera:
pdf (3) =01. * 2.718281828- (0.1 * 3)
pdf (3) =0.1 * 0.7408
pdf (3) =.07408 =~ 7.4%

En nuestro ejemplo, si asumimos una tasa de falla constante, que sigue la distribución exponencial, la distribución de la vida, o pdf para los motores eléctricos industriales, se expresa en la Figura 3. No se confunda por la naturaleza decreciente de la función pdf. Sí, la tasa de fallas es constante, pero el pdf asume matemáticamente fallas sin reemplazo, por lo que la población a partir de la cual pueden ocurrir fallas se reduce continuamente, acercándose asintóticamente a cero.

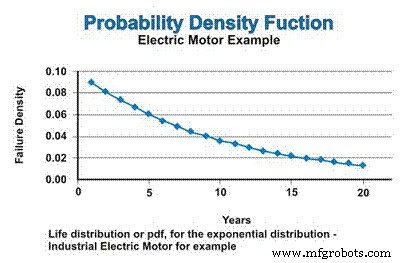
Figura 3. La función de densidad de probabilidad (pdf)

La función de distribución acumulativa (CDF) es simplemente el número acumulativo de fallas que uno podría esperar durante un período de tiempo. Para la distribución exponencial, la tasa de fallas es constante, por lo que la tasa relativa a la que se agregan los componentes fallados a la CDF permanece constante. Sin embargo, a medida que la población disminuye como resultado de una falla, el número real de fallas estimadas matemáticamente disminuye en función de la población en declive. Al igual que el pdf se acerca asintóticamente a cero, el CDF se acerca asintóticamente a uno (Figura 4).

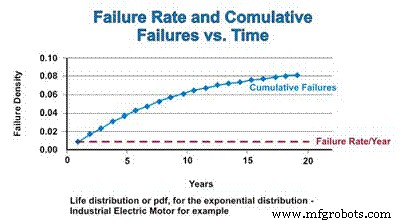
Figura 4. Tasa de fallas y función de distribución acumulativa

La parte de la tasa de falla decreciente de la curva de la bañera, que a menudo se denomina región de mortalidad infantil, y la región de desgaste se discutirán en la siguiente sección que trata sobre la distribución versátil de Weibull.

Distribución de Weibull

Desarrollado originalmente por Wallodi Weibull, un matemático sueco, el análisis de Weibull es fácilmente la distribución más versátil empleada por los ingenieros de confiabilidad. Si bien se llama distribución, en realidad es una herramienta que permite al ingeniero de confiabilidad caracterizar primero la función de densidad de probabilidad (distribución de frecuencia de falla) de un conjunto de datos de falla para caracterizar las fallas como vida temprana, constante (exponencial) o desgaste. (Gaussiano o logaritmo normal) trazando los datos del tiempo hasta la falla en un papel de trazado especial con el registro de los tiempos / ciclos / millas hasta la falla trazados en un eje X a escala logarítmica versus el porcentaje acumulativo de la población representado por cada falla en un registro -log escala eje Y (Figura 5).

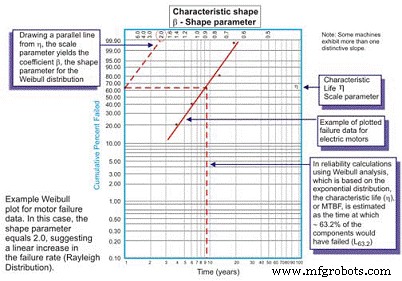
Figura 5. El diagrama de Weibull simple:anotado

Una vez trazada, la pendiente lineal de la curva resultante es una variable importante, denominada parámetro de forma, representada por â, que se utiliza para ajustar la distribución exponencial para que se ajuste a un amplio número de distribuciones de fallos. En general, si el coeficiente β, o parámetro de forma, es menor que 1.0, la distribución presenta fallas en la vida temprana o en la mortalidad infantil. Si el parámetro de forma excede aproximadamente 3,5, los datos dependen del tiempo e indican fallas de desgaste.

Este conjunto de datos asume típicamente la distribución gaussiana o normal. A medida que el coeficiente â aumenta por encima de ~ 3,5, la distribución en forma de campana se endurece, mostrando un aumento de la curtosis (punta en la parte superior de la curva) y una desviación estándar más pequeña. Muchos conjuntos de datos mostrarán dos o incluso tres regiones distintas.

Es común que los ingenieros de confiabilidad tracen, por ejemplo, una curva que representa el parámetro de forma durante la ejecución y otra curva para representar la tasa de falla constante o que aumenta gradualmente. En algunos casos, surge una tercera pendiente lineal distinta para identificar una tercera forma, la región de desgaste.

En estos casos, el pdf de los datos de falla de hecho asume la forma familiar de curva de bañera (Figura 6). La mayoría de los equipos mecánicos utilizados en las plantas, sin embargo, exhiben una región de mortalidad infantil y una región de tasa de falla constante o que aumenta gradualmente. Es raro ver emerger una curva que represente el desgaste. La vida característica, o η (minúscula griega "Eta"), es la aproximación de Weibull del MTBF. Siempre es en función del tiempo, millas o ciclos donde han fallado el 63.21% de las unidades en evaluación, que es el MTBF / MTTF para la distribución exponencial.

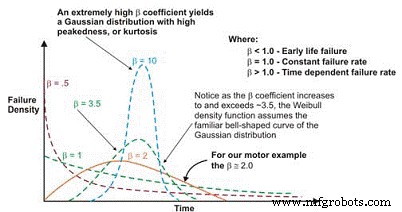
Figura 6. Dependiendo del parámetro de forma, la densidad de falla de Weibull La curva puede asumir varias distribuciones, que es lo que la hace tan versátil para la ingeniería de confiabilidad.

Como advertencia para vincular esta herramienta a la excelencia en el mantenimiento y la excelencia en las operaciones, si tuviéramos que controlar de manera más efectiva las funciones de fuerza que conducen a fallas mecánicas en cojinetes, engranajes, etc., tales como lubricación, control de contaminación, alineación, balance, funcionamiento adecuado, etc., más máquinas alcanzarían realmente su vida útil a la fatiga. Las máquinas que alcanzan su vida útil a la fatiga exhibirán la característica de desgaste familiar.

El uso del coeficiente β para ajustar la ecuación de la tasa de fallas en función del tiempo produce la siguiente ecuación general:

Dónde:
h (t) =Tasa de fallas (o tasa de riesgo) durante un tiempo determinado (t)
e =Base de los logaritmos naturales (2.718281828)
θ =MTBF / MTTF estimado
β =Parámetro de forma de Weibull de la gráfica.

Y, la siguiente función de confiabilidad:

Donde:
R (t) =Estimación de confiabilidad para un período de tiempo, ciclos, millas, etc. (t)
e =Base de los logaritmos naturales (2.718281828)
θ =MTBF / MTTF estimado
β =Parámetro de forma de Weibull de la gráfica.

Y la siguiente función de densidad de probabilidad (pdf):

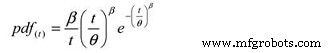
Dónde:
pdf (t) =Estimación de la función de densidad de probabilidad para un período de tiempo,
ciclos, millas, etc. (t)
e =Base de los logaritmos naturales (2.718281828)
θ =MTBF / MTTF estimado
β =Parámetro de forma de Weibull de la gráfica.

Cabe señalar que cuando β es igual a 1.0, la distribución de Weibull toma la forma de distribución exponencial en la que se basa.

Para los no iniciados, las matemáticas necesarias para realizar el análisis de Weibull pueden parecer abrumadoras. Pero una vez que comprendes la mecánica de las fórmulas, las matemáticas son realmente bastante simples. Además, el software hará la mayor parte del trabajo por nosotros hoy, pero es importante comprender la teoría subyacente para que el ingeniero de confiabilidad de la planta pueda implementar de manera efectiva la poderosa técnica de análisis de Weibull.

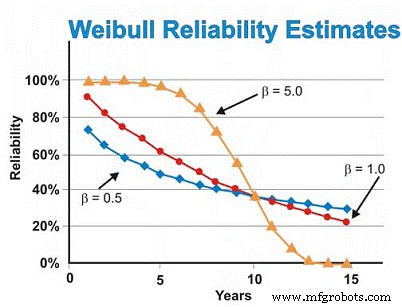
En nuestro ejemplo de motores eléctricos discutido anteriormente, asumimos previamente la distribución exponencial. Sin embargo, si el análisis de Weibull reveló fallas en la vida temprana al producir un parámetro de forma β de 0.5, la estimación de confiabilidad a los seis años sería ~ 46%, no el ~ 55% estimado asumiendo la distribución exponencial. Para reducir las fallas por desgaste, tendríamos que apoyarnos en nuestros proveedores para brindar calidad y confiabilidad mejor construidas y entregadas, almacenar mejor los motores para evitar la oxidación, corrosión, rozamiento y otros mecanismos de desgaste estático, y hacer un mejor trabajo de instalación y puesta en marcha de máquinas nuevas o reconstruidas.

Por el contrario, si el análisis de Weibull revelara que los motores presentaban fallas predominantemente relacionadas con el desgaste, lo que arrojaba un parámetro de forma β de 5.0, la estimación de confiabilidad a los seis años sería ~ 93%, en lugar del ~ 55% estimado asumiendo la distribución exponencial. Para fallas de desgaste dependientes del tiempo, podemos realizar una revisión o reemplazo programados asumiendo que tenemos una buena estimación del MTBF / MTTF después de haber alcanzado la región de desgaste y una desviación estándar lo suficientemente pequeña como para tomar decisiones de reconstrucción / reemplazo de alta confianza que no son excesivamente costosos.

En nuestro ejemplo de motor, asumiendo un parámetro de forma β de 5.0, la tasa de falla comienza a aumentar rápidamente después de unos cinco o seis años, por lo que es posible que deseemos editar nuestros datos para enfocarnos solo en la región de desgaste al estimar el reemplazo o la reconstrucción basada en el tiempo. hora. Alternativamente, podemos mejorar el diseño, apuntando al modo o modos de falla dominantes con el objetivo de disminuir las interferencias de "tensión-fuerza". En otras palabras, podemos intentar eliminar las debilidades de la máquina mediante la modificación del diseño, con el objetivo de eliminar lo que sea que esté causando las fallas dependientes del tiempo.

Asumiendo que todo es constante, excepto el parámetro de forma β, la Figura 7 ilustra la diferencia que tiene el parámetro de forma β en la estimación de confiabilidad asumiendo valores de forma β de 0.5 (vida temprana), 1.0 (constante o exponencial) y 5.0 (desgaste) para un rango de estimaciones de tiempo. Este gráfico ilustra visualmente el concepto de riesgo creciente versus tiempo (β =0.5), riesgo constante versus tiempo (β =1.0) y riesgo creciente versus tiempo (β =5).

Figura 7. Varias proyecciones de confiabilidad en función del tiempo para diferentes Parámetros de forma de Weibull

La trama de Weibull de varias pendientes

Con frecuencia, al dibujar una línea de regresión de mejor ajuste a través de los puntos de datos en una gráfica de Weibull, el coeficiente de correlación es pobre, lo que significa que los puntos de datos reales se desvían una gran distancia de la línea de regresión. Esto se evalúa examinando el coeficiente de correlación R, o más conservadoramente, R2, que denota variabilidad de los datos. Cuando la correlación es pobre, el ingeniero de confiabilidad debe examinar los datos para evaluar si existen dos o más patrones, lo que puede indicar diferencias importantes en los modos de falla, contexto operativo, etc. A menudo, esto produce dos o más estimaciones de beta (Figura 8).

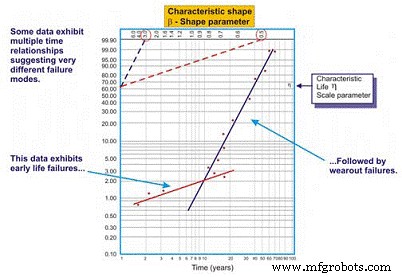
Figura 8. Un ejemplo de un diagrama de Weibull multi-beta

Como vemos en nuestro ejemplo en la Figura 8, el conjunto de datos funciona mejor cuando se dibujan dos líneas de regresión distintas. La primera línea exhibe un parámetro de forma beta de 0.5, lo que sugiere fallas en la vida temprana. La segunda línea presenta una forma beta de 3.0, lo que sugiere que el riesgo de falla aumenta en función del tiempo. Es común que los equipos complejos, particularmente los equipos mecánicos, experimenten fallas de "rodaje" cuando son nuevos o recientemente reconstruidos. Como tal, el riesgo de falla es mayor justo después de la puesta en marcha inicial.

Una vez que el sistema funciona a través de su período de ejecución, que puede tomar minutos, horas, días, semanas, meses o años, según el tipo de sistema, el sistema ingresa a un patrón de riesgo diferente. En este ejemplo, el sistema ingresa a un período en el que el riesgo de falla aumenta en función del tiempo una vez que el sistema sale de su período de ejecución.

La multi-beta ofrece al ingeniero de confiabilidad una estimación más precisa del riesgo en función del tiempo. Armado con este conocimiento, él o ella está mejor posicionado para tomar acciones de mitigación. Por ejemplo, durante el período de vida temprana, estaríamos inclinados a mejorar la precisión con la que fabricamos / reconstruimos, instalamos y ponemos en marcha. Además, podríamos agregar técnicas de monitoreo y / o aumentar nuestra frecuencia de monitoreo durante el período de alto riesgo. Después del período de rodaje, podríamos introducir técnicas de monitoreo que estén dirigidas a las fallas de desgaste dependientes del tiempo que se cree que afectan el sistema, aumentar la frecuencia de monitoreo en consecuencia o programar acciones de mantenimiento preventivo "difíciles" en algunos casos.

Estimación de la confiabilidad del sistema

Una vez que se ha establecido la confiabilidad de los componentes o máquinas en relación con el contexto operativo y el tiempo de misión requerido, los ingenieros de la planta deben evaluar la confiabilidad de un sistema o proceso. Nuevamente, en aras de la brevedad y la simplicidad, analizaremos las estimaciones de confiabilidad del sistema para sistemas redundantes en serie, en paralelo y de carga compartida (sistemas r / n).

Sistemas en serie
Antes de discutir los sistemas en serie, deberíamos discutir los diagramas de bloques de confiabilidad. No es una herramienta complicada de usar, los diagramas de bloques de confiabilidad simplemente mapean un proceso de principio a fin. Para un sistema en serie, al subsistema A le sigue el subsistema B y así sucesivamente. En el sistema en serie, la capacidad de emplear el Subsistema B depende del estado operativo del Subsistema A. Si el Subsistema A no está funcionando, el sistema no funciona independientemente de la condición del Subsistema B (Figura 9).

To calculate the system reliability for a serial process, you only need to multiply the estimated reliability of Subsystem A at time (t) by the estimated reliability of Subsystem B at time (t). The basic equation for calculating the system reliability of a simple series system is:

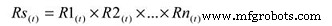
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

So, for a simple system with three subsystems, or sub-functions, each having an estimated reliability of 0.90 (90%) at time (t), the system reliability is calculated as 0.90 X 0.90 X 0.90 =0.729, or about 73%.

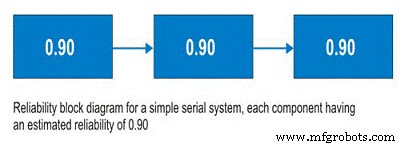
Figure 9. Simple Serial System

Parallel Systems
Often, design engineers will incorporate redundancy into critical machines. Reliability engineers call these parallel systems. These systems may be designed as active parallel systems or standby parallel systems. The block diagram for a simple two component parallel system is shown in Figure 10.

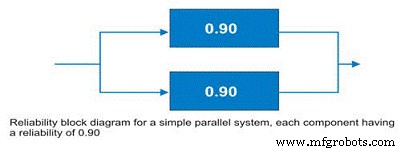
Figure 10. Simple parallel system – the system reliability is increased to 99% due to the redundancy.

To calculate the reliability of an active parallel system, where both machines are running, use the following simple equation:

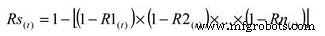
Where:
Rs(t) – System reliability for given time (t)
R1-n(t) – Subsystem or sub-function reliability for given time (t)

The simple parallel system in our example with two components in parallel, each having a reliability of 0.90, has a total system reliability of 1 – (0.1 X 0.1) =0.99. So, the system reliability was significantly improved.

There are some shortcut methods for calculating parallel system reliability when all subsystems have the same estimated reliability. More often, systems contain parallel and serial subcomponents as depicted in Figure 11. The calculation of standby systems requires knowledge about the reliability of the switching mechanism. In the interest of simplicity and brevity, this topic will be reserved for a future article.

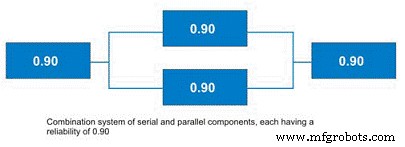
Figure 11. Combination System with Parallel and Serial Elements

r out of n Systems (r/n Systems)
An important concept to plant reliability engineers is the concept of r/n systems. These systems require that r units from a total population in n be available for use. A great industrial example is coal pulverizers in an electric power generating plant. Often, the engineers design this function in the plant using an r/n approach. For instance, a unit has four pulverizers and the unit requires that three of the four be operable to run at the unit’s full load (see Figure 12).

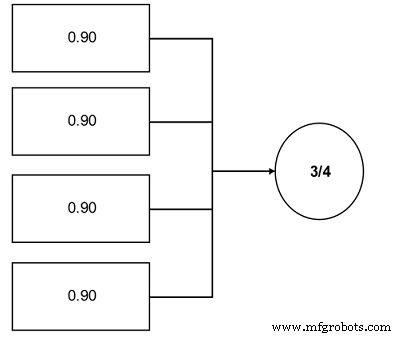
Figure 12. Simple r/n system example – Three of the four components are required.

The reliability calculation for an r/n system can be reduced to a simple cumulative binomial distribution calculation, the formula for which is:

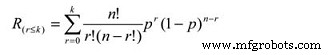
Where:
Rs =System reliability given the actual number of failures (r) is less than or equal the maximum allowable (k)
r =The actual number of failures
k =The maximum allowable number of failures
n =The total number of units in the system
p =The probability of survival, or the subcomponent reliability for a given time (t).

This equation is somewhat more complicated. In our pulverizer example, assuming a subcomponent reliability of 0.90, the equation works out as a summation of the following:
P(0) =0.6561
P(1) =0.2916

So, the likelihood of completing the mission time (t) is 0.9477 (0.6561 + 0.2916), or approximately 95%.

Field Data Collection
To employ the reliability analysis methods described herein, the engineer requires data. It is imperative to establish field data collection systems to support your reliability management initiatives. Likewise, as much as possible, you’ll want to employ common nomenclature and units so that your data can be parsed effectively for more detailed analysis. Collect the following information:

• Basic System Information
• Operating Context
• Environmental Context
• Failure Data

A good general system for data collection is described in the IEC standard 300-3-2. In addition to providing instructions for collecting field data, it provides a standard taxonomy of failure modes. Other taxonomies have been established, but the IEC standard represents a good starting point for your organization to define its own. Likewise, DOE standard NE-1004-92 offers a very nice standard nomenclature of failure causes.

An important benefit derived from your efforts to collect good field data is that it enables you to break the “random trap.” As I mentioned earlier, the bathtub curve has been much maligned – particularly in the Reliability-Centered Maintenance literature. While it’s true that Weibull analysis reveals that few complex mechanical systems exhibit time-dependent wearout failures, the reason, at least in part, is due to the fact that the reliability of complex systems is affected by a wide variety of failure modes and mechanisms.

When these are lumped together, there is a “randomizing” effect, which makes the failures appear to lack any time dependency. However, if the failure modes were analyzed individually, the story would likely be very different (Figure 13). For certain, some failure modes would still be mathematically random, but many, and arguably most, would exhibit a time dependency. This kind of information would arm reliability engineers and managers with a powerful set of options for mitigating failure risk with a high degree of precision. Naturally, this ability depends upon the effective collection and subsequent analysis of field data.

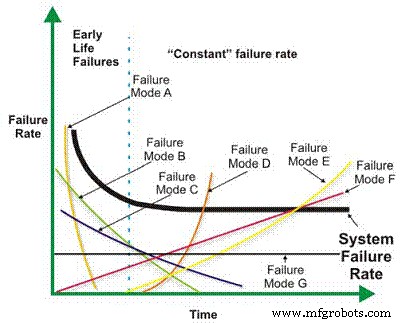
Figure 13. Good field data collection enables you to break the random trap.

This brief introduction to reliability engineering methods is intended to expose the otherwise uninitiated plant engineer to the world of quantitative reliability engineering. The subject is quite broad, however, and I’ve only touched on the major reliability methods that I believe are most applicable to the plant engineer. I encourage you to further investigate the field of reliability engineering methods, concentrating on the following topics, among others:

• More detailed understanding of the Weibull distribution and its applications

• More detailed understanding of the exponential distribution and its applications

• The Gaussian distribution and its applications

• The log-normal distribution and its applications

• Confidence intervals (binomial, chi-square/Poisson, etc.)

• Beta distribution and its applications

• Bayesian applications of reliability engineering methods

• Stress-strength interference analysis

• Testing options and their applicability to plant reliability engineering

• Reliability growth strategies and management

• More detailed understanding of field data collection.

Most important, spend time learning how to apply reliability engineering methods to plant reliability problems. If your interest in reliability engineering methods is high, I encourage you to pursue professional certification by the American Society for Quality as a reliability engineer (CRE).

References
Troyer, D. (2006) Strategic Plant Reliability Management Course Book, Noria Publishing, Tulsa, Oklahoma.

Bernowski, K (1997) “Safety in the Skies,” Quality Progress , January.

Dovich, R. (1990) Reliability Statistics, ASQ Quality Press, Milwaukee, WI.

Krishnamoorthi, K.S. (1992) Reliability Methods for Engineers, ASQ Quality Press , Milwaukee, WI.

MIL Standard 721

IEC Standard 300-3-3

DOE Standard NE-1004-92

Appendix:Select reliability engineering terms from MIL STD 721
Availability – A measure of the degree to which an item is in the operable and committable state at the start of the mission, when the mission is called for at an unknown state.

Capability – A measure of the ability of an item to achieve mission objectives given the conditions during the mission.

Dependability – A measure of the degree to which an item is operable and capable of performing its required function at any (random) time during a specified mission profile, given the availability at the start of the mission.

Failure – The event, or inoperable state, in which an item, or part of an item, does not, or would not, perform as previously specified.

Failure, dependent – Failure which is caused by the failure of an associated item(s). Not independent.

Failure, independent – Failure which occurs without being caused by the failure of any other item. Not dependent.

Failure mechanism – The physical, chemical, electrical, thermal or other process which results in failure.

Failure mode – The consequence of the mechanism through which the failure occurs, i.e. short, open, fracture, excessive wear.

Failure, random – Failure whose occurrence is predictable only in the probabilistic or statistical sense. This applies to all distributions.

Failure rate – The total number of failures within an item population, divided by the total number of life units expended by that population, during a particular measurement interval under stated conditions.

Maintainability – The measure of the ability of an item to be retained or restored to specified condition when maintenance is performed by personnel having specified skill levels, using prescribed procedures and resources, at each prescribed level of maintenance and repair.

Maintenance, corrective – All actions performed, as a result of failure, to restore an item to a specified condition. Corrective maintenance can include any or all of the following steps:localization, isolation, disassembly, interchange, reassembly, alignment and checkout.

Maintenance, preventive – All actions performed in an attempt to retain an item in a specified condition by providing systematic inspection, detection and prevention of incipient failures.

Mean time between failure (MTBF) – A basic measure of reliability for repairable items:the mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to failure (MTTF) – A basic measure of reliability for non-repairable items:The mean number of life units during which all parts of the item perform within their specified limits, during a particular measurement interval under stated conditions.

Mean time to repair (MTTR) – A basic measure of maintainability:the sum of corrective maintenance times at any specified level of repair, divided by the total number of failures within an item repaired at that level, during a particular interval under stated conditions.

Mission reliability – The ability of an item to perform its required functions for the duration of specified mission profile.

Reliability – (1) The duration or probability of failure-free performance under stated conditions. (2) The probability that an item can perform its intended function for a specified interval under stated conditions. For non-redundant items this is the equivalent to definition (1). For redundant items, this is the definition of mission reliability.