Una expresión desarrollada de potencial químico para una deformación rápida en electrodos de nanopartículas de baterías de iones de litio

Métodos

Ecuaciones mecánicas

La inserción de litio en electrodos puede provocar cambios volumétricos. Por conveniencia, empleamos dos formas de describir la deformación y el movimiento de los sólidos, a saber, la descripción lagrangiana y la descripción euleriana. El movimiento de las partículas de material en un medio continuo se puede describir mediante

donde x son las coordenadas de Euler, X son las coordenadas de Lagrange y U es el campo de desplazamiento. El cambio en la forma del sólido continuo se puede caracterizar por el tensor del gradiente de deformación, dado por

donde Grad representa el operador de gradiente en la descripción lagrangiana y I es el tensor unitario de segundo orden.

Para una partícula esférica, las coordenadas de Lagrange y las coordenadas de Euler de un punto material son (R, Θ, Φ) y (r, θ, φ) respectivamente en el sistema esférico. Luego, el tensor de gradiente de deformación F se encuentra como

Durante la carga o descarga, el cambio de forma del electrodo se puede dividir en dos procesos:(a) un cambio de forma debido al inserto de litio y (b) una deformación elástica reversible. Estos dos procesos de deformación se pueden describir mediante dos tensores de gradiente separados y el tensor de gradiente de deformación total se puede escribir como

donde F ^e representa la deformación elástica, F ^c representa el cambio de forma debido a la inserción de litio. La ecuación (4) representa el proceso del material del electrodo desde el estado inicial (no deformado) al estado actual (deformado). Suponiendo que el cambio de forma debido al inserto de litio es isotrópico, F ^c puede ser dado por

donde Ω representa el volumen molar parcial.

De la ecuación. (3–5), el tensor de gradiente de deformación elástica F ^e es

El tensor de deformación total de Green-Lagrange E se puede escribir como

donde el tensor de deformación elástica E ^e y tensor de deformación inducida por difusión E ^c son

respectivamente.

Sustituyendo la ecuación. (6) en la ecuación. (8), los componentes radial y tangencial del tensor de deformación de Green-Lagrange son

La relación constitutiva para la deformación se puede determinar a partir de la densidad de energía de deformación como

donde W es la densidad de energía de deformación elástica en la descripción de Lagrange, y P es el primer estrés de Piola-Kirchhoff. Además, si el material es linealmente elástico, W se puede escribir como una función cuadrática del tensor de deformación de Green-Lagrange

Aquí, E _h y ν son el módulo de Young y la relación de Poisson, respectivamente, C es el tensor de rigidez y det ( F ^c ) es el determinante del tensor del gradiente de deformación para la deformación inducida por difusión.

Finalmente, el primer estrés de Piola-Kirchhoff viene dado por

Combinando Ecs. (5), (9), (10) y (13), los componentes correspondientes del primer tensor de tensión Piola-Kirchhoff (P-K) son

Y la primera tensión P-K debe satisfacer la condición de equilibrio en ausencia de fuerza corporal

con condiciones iniciales y de contorno

Ecuación de transporte masivo

La concentración y el flujo de difusión del litio en los electrodos, que son funciones de coordenadas y tiempo, se denominarán C ( X , T) y J ( X , T) en la descripción de Lagrange, y deberían estar satisfechos con la ecuación de transporte de masa escrita como

donde Div representa el operador de divergencia en la descripción lagrangiana. Considerando la característica de la simetría esférica, la difusión ocurre solo en la dirección radial y usamos J ( R , t) para representar el componente radial de J ( X , t). En el sistema esférico, Eq. (18) se convierte en

La difusión de litio en los electrodos es impulsada por el gradiente de potencial químico y el flujo radial J ( R , t) es proporcional al gradiente de potencial químico μ , como [11]

donde D es la difusividad, R _g es la constante de gas y T es la temperatura. μ se define como la desviación de la densidad de energía total a la concentración y se puede escribir como

Suponga que la densidad de energía del sistema, Π, se puede describir como la suma de la densidad de energía química y la densidad de energía de deformación. Entonces, la densidad de energía interna total se puede escribir como

Sustituyendo la ecuación. (22) en la ecuación (21), el potencial químico μ se puede demostrar que es

donde μ ₀ ( C ) y τ ( E ^e , C ) son las partes del potencial químico independientes y dependientes de la tensión, respectivamente. Y

donde μ ₀ es una constante que representa el potencial químico en un estado estándar, y γ es el coeficiente de actividad que representa los efectos de las interacciones entre los átomos / moléculas. Para una solución diluida, las interacciones entre los átomos / moléculas son insignificantes; por tanto, γ =1.

Nos centramos en la parte del potencial químico que depende del estrés τ ( E ^e , C), que es la derivada de la densidad de energía de deformación W con respecto a la concentración de litio C. Tradicionalmente, Π ( X , T) se considera la densidad de energía libre de Helmholtz y, por lo tanto, este paso se lleva a cabo para la deformación fija escrita como [11]

El subíndice H significa que es causado por la densidad de energía libre de Helmholtz. El potencial químico resulta ser

donde σ _m es la tensión hidrostática de Cauchy en la descripción euleriana y se puede obtener mediante

Vale la pena señalar que la rigidez C del material del electrodo se supone que es independiente de la concentración de litio C en Eq. (12). Además, det ( F ^e ) ≈ 1 es ampliamente aceptado, por lo que generalmente se ignora. En el resto de este artículo, llamamos Eq. (26) como expresión tradicional del potencial químico. Por otro lado, Π ( X , T) se considera que es la densidad de energía libre de Gibbs en algunos estudios [12, 13] sobre el modelo de campo de fase, por lo que no podemos obtener una expresión desarrollada de τ ( E ^e , C) y

El subíndice G significa que es causado por la densidad de energía libre de Gibbs. En este caso, μ se convierte en

y llamamos Eq. (29) como la expresión desarrollada del potencial químico.

La ecuación de transporte de masa está formada por las ecuaciones. (19), (20), (26) y (29) con expresiones tradicionales y desarrolladas de potencial químico. En la parte restante de este artículo, compararemos los efectos de estas dos expresiones de potencial químico sobre el estrés inducido por difusión y la concentración de Li bajo diferentes métodos de carga.

En termodinámica, la energía libre de Helmholtz es un potencial termodinámico que mide el trabajo útil obtenible de un sistema termodinámico cerrado a temperatura y volumen constantes. Por el contrario, la energía libre de Gibbs mide el máximo de trabajo reversible que puede realizar un sistema termodinámico a temperatura y presión constantes. En sólidos con bajo nivel de tensión, la energía libre de Gibbs es aproximadamente equivalente a la energía libre de Helmholtz, porque la deformación de los sólidos suele ser pequeña. Esta suposición es adecuada para la mayoría de los materiales sólidos debido a su pequeña deformación inducida por difusión, pero excepto para el silicio debido a su gran expansión volumétrica durante la litiación. De hecho, la difusión y la deformación tienen lugar al mismo tiempo, por lo que no es adecuado suponer que no se produce ninguna deformación mientras cambia la concentración. Aun así, como puede verse en la ecuación. (25), la expresión tradicional de potencial químico sigue siendo precisa cuando la tasa de deformación es lo suficientemente baja. Sin embargo, es probable que cause grandes errores cuando un electrodo de nanopartículas de Si se litiga rápidamente.

El electrodo está litiado con una concentración constante de iones de litio en su superficie, es decir, la operación potenciostática, o con un flujo constante en su superficie, es decir, la operación galvanostática. Las condiciones de contorno de la ecuación. (19) son

respectivamente. La condición inicial está escrita como

para cada operación de carga. Aquí, C _máx es la concentración máxima de litio del material y j ₀ es una constante que representa la corriente de carga.

Implementación numérica

Es muy difícil obtener la solución analítica del sistema anterior que consiste en ecuaciones diferenciales parciales, si no imposible. Con Ecs. (1) - (3) y (13) - (18), calculamos numéricamente la evolución de la tensión inducida por difusión y la concentración de litio utilizando el software multifísico COMSOL. Se estudia la litiación de un nanoelectrodo de silicio bajo operaciones tanto potenciostáticas como galvanostáticas, con diferentes expresiones de potencial químico. Las propiedades del material de Si y los parámetros operativos utilizados en la simulación se enumeran en la Tabla 1. Por conveniencia, en las figuras se utiliza la correspondiente sustitución adimensional de coordenada, tensión y concentración.

Para investigar la diferencia entre las diferentes expresiones de potencial químico en diferentes momentos en el electrodo esférico de Si, el estado de carga (SOC) se calcula como

Los flujos de difusión inducidos por estrés en la descripción lagrangiana se describen como

que representa el flujo causado por diferentes expresiones de potencial químico, respectivamente.

Resultados y discusión

La Figura 1 muestra la distribución espacial de la concentración de litio, la tensión radial y la tensión del aro en un electrodo esférico de Si bajo operación galvanostática en varios SOC. A modo de comparación, se incluyen los resultados numéricos con las expresiones desarrolladas y tradicionales del potencial químico y se representan mediante líneas continuas y símbolos de triángulos, respectivamente. Para cada SOC en la Fig. 1a, la línea continua casi se superpone a los símbolos del triángulo. Se puede ignorar el efecto causado por las diferentes expresiones del potencial químico sobre la concentración de litio. En la Fig. 1b y la Fig. 1c, para los SOC de 46,7% y 65,5%, las líneas continuas son más altas que los triángulos del centro, mientras que casi se superponen en el exterior, al igual que en otros SOC. En general, hay un ligero efecto sobre la concentración de litio y las tensiones durante el funcionamiento galvanostático. La Figura 2 muestra las distribuciones espaciales de la concentración de litio, tensión radial y tensión de aro en un electrodo esférico de Si bajo operación potenciostática en varios SOC. Vale la pena mencionar que las tensiones radiales y de aro primero aumentan y luego disminuyen con el aumento del SOC tanto en la Fig. 1 como en la Fig. 2. Es porque el electrodo de silicio en el estado inicial o en el estado completamente litiado está libre de tensiones, ya que no hay gradiente de concentración. En comparación con la figura 1a, la diferencia entre líneas continuas y triángulos es mayor en la figura 2a. Debido a que la concentración de litio en la superficie es un C constante _máx en funcionamiento potenciostático, la tasa de carga es más alta que la tasa de deformación que en la operación galvanostática y también la tasa de deformación. Sin embargo, la deformación total bajo el mismo SOC es casi la misma independientemente del método de carga, solo que toma un tiempo diferente. Indica que la influencia en la distribución del litio causada por diferentes expresiones de potencial químico solo está relacionada con la tasa de deformación más que con la deformación y aumenta con el aumento de la tasa de deformación. De hecho, los experimentos existentes muestran que los electrodos de silicio se deforman muy rápidamente durante la litiación bajo ciertos modos de carga. Como podemos ver en la Fig. 3 [17], el ánodo de Si se deforma completamente en 1 min con un potencial de 2 V con respecto al metal Li. En esta condición, los resultados resueltos por estas dos expresiones de potencial químico serán significativamente diferentes. Desafortunadamente, en este caso, la tensión del electrodo no se puede medir con precisión y, por lo tanto, no se puede comparar cuantitativamente con nuestro modelo.

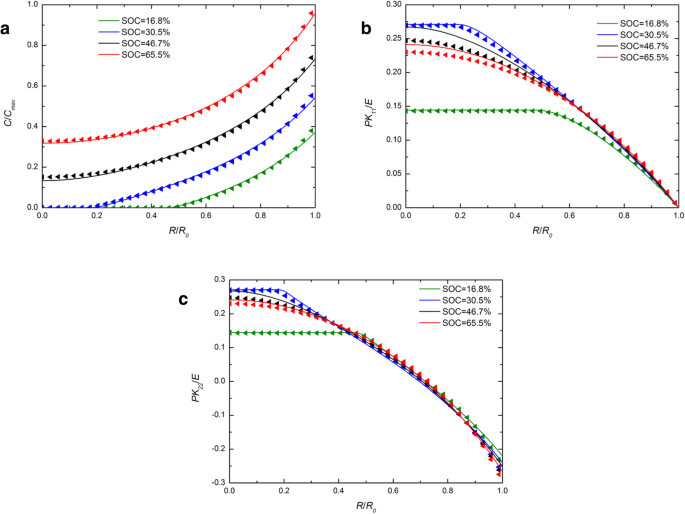
Distribución espacial de ( a ) la concentración de litio, ( b ) tensión radial y ( c ) tensión de aro en un electrodo esférico de Si en diferentes SOC bajo operación galvanostática (las líneas continuas representan los resultados con la expresión tradicional del potencial químico; las líneas triangulares representan los resultados con la expresión desarrollada del potencial químico)

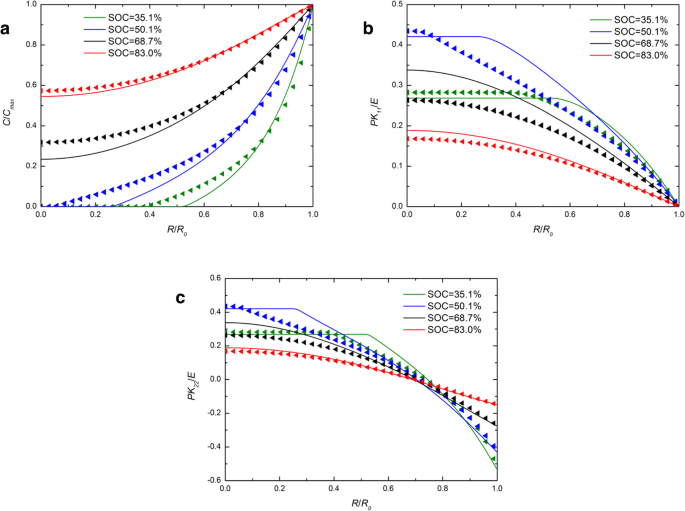
Distribución espacial de ( a ) la concentración de litio, ( b ) tensión radial y ( c ) tensión de aro en un electrodo esférico de nanopartículas de Si en diferentes SOC bajo operación potenciostática (las líneas continuas representan los resultados con la expresión tradicional del potencial químico; las líneas triangulares representan los resultados con la expresión desarrollada del potencial químico)

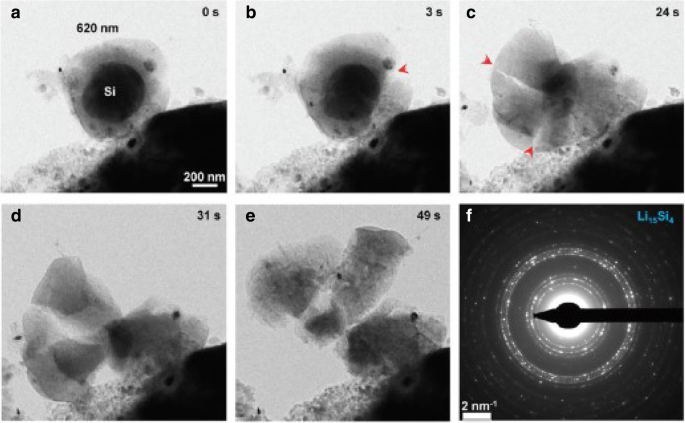
Deformación rápida de un SiNP autónomo de 620 nm durante litiación química en 1 min. un - e Secuencia de tiempo de inicio y crecimiento de grietas. f EDP ​​que indica la formación de Li ₁₅ policristalino Si ₄ como la fase completamente litiada

La Figura 4 muestra la distribución espacial de J _H / J _G en un electrodo esférico de Si en diferentes SOC en funcionamiento galvanostático con diferentes j . En la Fig. 4, las líneas continuas casi coinciden con los triángulos, lo que indica que diferentes expresiones de potencial químico tienen un ligero efecto en la relación de J _H y J _G . Es evidente que el rango de los valores de J _H / J _G aumenta con el aumento de la corriente de carga. Esto se debe a que la corriente de carga más grande conduce a tasas de deformación más altas y, por lo tanto, provoca un mayor impacto de diferentes expresiones de potencial químico. La relación es siempre mayor que 1 en el centro y menor que 1 en la superficie. Sugiere que el flujo obtenido de la expresión desarrollada del potencial químico en la superficie es mayor que el obtenido de la expresión tradicional, mientras que en el centro ocurre lo contrario. Observamos que todas las líneas continuas y los triángulos de la figura 4 casi se cruzan con un punto. Además, la relación correspondiente a la intersección es siempre aproximadamente 1, independientemente de la corriente con la que se cargue el electrodo. Sugiere que hay un radio crítico donde el flujo se ve menos afectado por las diferentes expresiones de potencial químico. Lo llamamos región independiente del potencial químico (CIR). Obviamente, CIR siempre está cerca de la superficie del electrodo esférico y está más cerca de la superficie a medida que aumenta la corriente de carga.

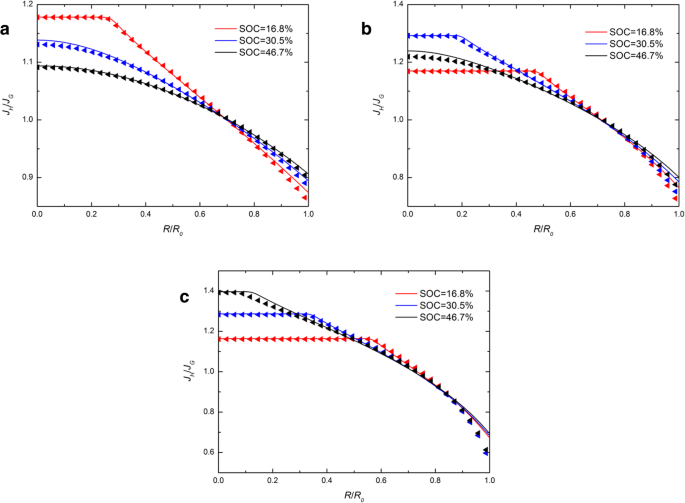
Distribución espacial de J _H / J _G en un electrodo esférico de nanopartículas de Si en diferentes SOC en funcionamiento galvanostático con ( a ) j =0.5 j ₀ , ( b ) j = j ₀ y ( c ) j =1,5 j ₀ (las líneas continuas representan los resultados con la expresión tradicional del potencial químico; los triángulos representan los resultados con la expresión desarrollada del potencial químico)

Comparando los potenciales químicos tradicionales y desarrollados en la Ec. (26) y Eq. (29), se encuentra que la tensión hidrostática de Cauchy σ _m es la clave de la diferencia entre estas dos expresiones. Para investigar las causas de CIR, la distribución espacial de σ _m / E en un electrodo esférico de Si en diferentes SOC bajo operación galvanostática con diferentes expresiones de potencial químico se dan en la Fig. 5 y la Fig. 6. Obviamente, casi todas las curvas se cruzan en un punto en CIR y la tensión hidrostática de Cauchy σ _m está cerca de 0 en este punto, excepto al inicio de la carga (SOC =6.2%). Indica que σ _m en CIR se mantiene en un nivel bajo (casi 0) durante la mayor parte del período de carga. Se puede interpretar que las dos expresiones de potencial químico son casi equivalentes cuando la tensión hidrostática σ _m está cerca de 0. Esto puede explicar en parte por qué aparece CIR, pero no es suficiente para explicar las características de las curvas en σ _m . Debe resolverse con nuestra próxima investigación.

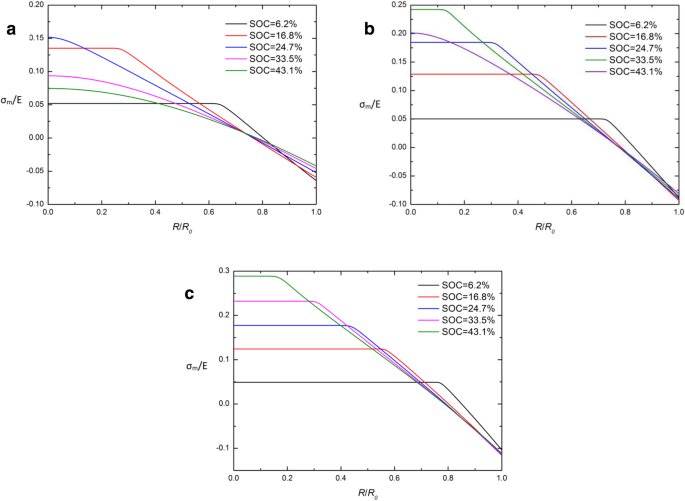
Distribución espacial de σ _m / E en un electrodo esférico de nanopartículas de Si en diferentes SOC bajo operación galvanostática con la expresión tradicional de potencial químico y ( a ) j =0.5 j ₀ , ( b ) j = j _0, y ( c ) j =1,5 j ₀

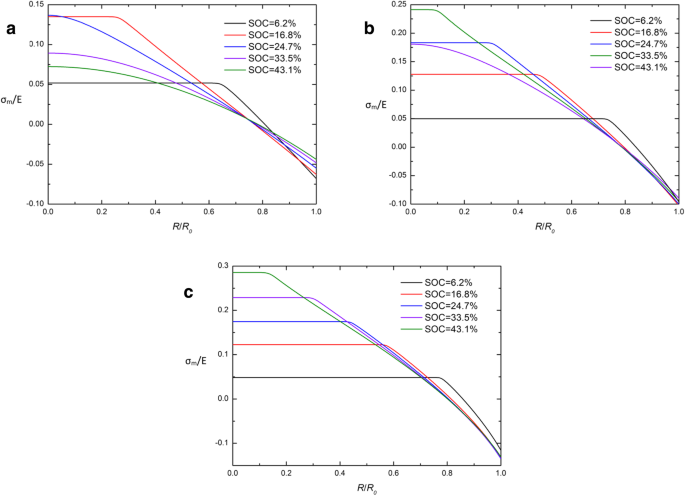
Distribución espacial de σ _m / E en un electrodo esférico de nanopartículas de Si en diferentes SOC bajo operación galvanostática con la expresión desarrollada de potencial químico ( a ) j =0.5 j ₀ , ( b ) j = j ₀ y ( c ) j =1,5 j ₀ s

Conclusiones

En este trabajo, se propone una expresión desarrollada de potencial químico sin el supuesto de baja tasa de deformación, que se distingue de la expresión desarrollada que se usa ampliamente en la actualidad. La diferencia entre las expresiones tradicionales y desarrolladas de potencial químico en las distribuciones de tensión y concentración en electrodos de nanopartículas de Si se analiza en las operaciones tanto potenciostáticas como galvanostáticas.

El resultado revela que el efecto causado por diferentes expresiones de potencial químico puede despreciarse en la operación galvanostática, pero es significativo en la operación potenciostática. Se encuentra que el efecto está simplemente relacionado con la tasa de deformación más que con la deformación, y puede ser mayor con el aumento de la tasa de deformación. Considerando el supuesto de baja tasa de deformación en la expresión del potencial químico tradicional, se cree que los resultados obtenidos por la expresión del potencial químico desarrollado son más confiables. Cerca de la superficie del electrodo de nanopartículas se encuentra una región independiente del potencial químico (CIR), donde el flujo causado por el potencial químico tradicional y desarrollado es casi el mismo durante la mayor parte del proceso litiado. Además, CIR está más cerca de la superficie con los aumentos de la corriente de carga. Un fenómeno similar también aparece en las curvas de tensión hidrostática de Cauchy. La tensión hidrostática de Cauchy σ _m mantiene una constante y se mantiene a un nivel bajo (casi 0) en CIR en la mayor parte del tiempo, sin importar qué expresión de potencial químico se utilice. Estos resultados aún no se han informado en la literatura.

Disponibilidad de datos y materiales

Los conjuntos de datos analizados durante el estudio actual están disponibles del autor correspondiente a solicitud razonable.

Abreviaturas

CIR:

Una región donde el flujo de difusión causado por estas dos expresiones de potencial químico es casi el mismo

Mini revisión sobre dispositivos electrónicos flexibles y portátiles para monitorear la información de salud humana Transporte de electrones mejorado de la interfaz del cátodo PF-NR2 mediante nanopartículas de oro