Circuitos paralelos simples

En esta página, describiremos los tres principios que debe comprender con respecto a los circuitos en paralelo:

1. Voltaje: El voltaje es igual en todos los componentes de un circuito en paralelo.
2. Actual: La corriente total del circuito es igual a la suma de las corrientes de las ramas individuales.
3. Resistencia: Las resistencias individuales disminuyen para igualar una resistencia total menor en lugar de agregar para hacer el total.

Echemos un vistazo a algunos ejemplos de circuitos paralelos que demuestran estos principios.

Comenzaremos con un circuito paralelo que consta de tres resistencias y una sola batería:

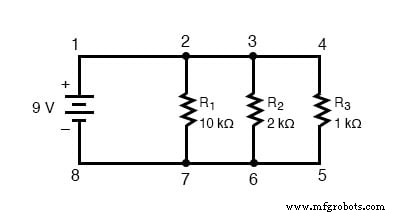
Voltaje en circuitos en paralelo

El primer principio que se debe comprender sobre los circuitos en paralelo es que el voltaje es igual en todos los componentes del circuito . Esto se debe a que solo hay dos conjuntos de puntos comunes eléctricamente en un circuito paralelo, y el voltaje medido entre conjuntos de puntos comunes debe ser siempre el mismo en un momento dado.

Por lo tanto, en el circuito anterior, el voltaje en R ₁ es igual al voltaje en R ₂ que es igual al voltaje en R ₃ que es igual al voltaje en la batería.

Esta igualdad de voltajes se puede representar en otra tabla para nuestros valores iniciales:

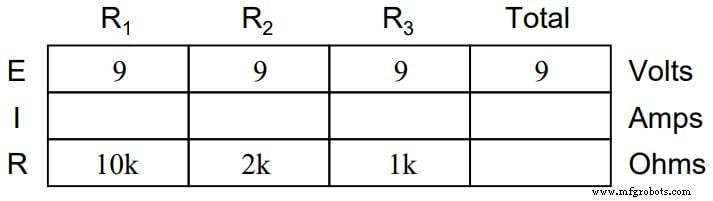
Aplicaciones de la ley de Ohm para circuitos paralelos simples

Al igual que en el caso de los circuitos en serie, se aplica la misma advertencia para la ley de Ohm:los valores de voltaje, corriente y resistencia deben estar en el mismo contexto para que los cálculos funcionen correctamente.

Sin embargo, en el circuito de ejemplo anterior, podemos aplicar inmediatamente la Ley de Ohm a cada resistor para encontrar su corriente porque conocemos el voltaje en cada resistor (9 voltios) y la resistencia de cada resistor:

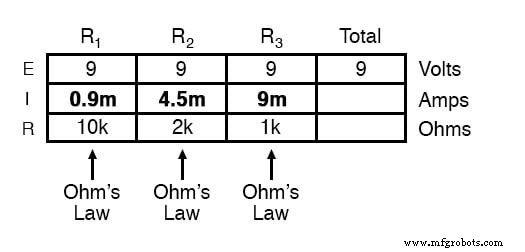
En este punto, todavía no sabemos cuál es la corriente total o la resistencia total para este circuito en paralelo, por lo que no podemos aplicar la Ley de Ohm a la columna de la derecha ("Total"). Sin embargo, si pensamos detenidamente en lo que está sucediendo, debería resultar evidente que la corriente total debe ser igual a la suma de todas las corrientes de resistencias individuales ("ramales"):

A medida que la corriente total sale del terminal positivo (+) de la batería en el punto 1 y viaja a través del circuito, parte del flujo se divide en el punto 2 para pasar por R ₁ , algunos más se separan en el punto 3 para pasar por R ₂ , y el resto pasa por R ₃ . Como un río que se ramifica en varios arroyos más pequeños, los caudales combinados de todos los arroyos deben ser iguales al caudal de todo el río.

Lo mismo se encuentra donde las corrientes a través de R ₁ , R ₂ y R ₃ unirse para fluir de regreso al terminal negativo de la batería (-) hacia el punto 8:el flujo de corriente desde el punto 7 al punto 8 debe ser igual a la suma de las corrientes (derivadas) a través de R ₁ , R ₂ y R ₃ .

Este es el segundo principio de los circuitos en paralelo: la corriente total del circuito es igual a la suma de las corrientes de rama individuales .

Usando este principio, podemos completar el espacio de TI en nuestra tabla con la suma de I _R1 , Yo _R2 y yo _R3 :

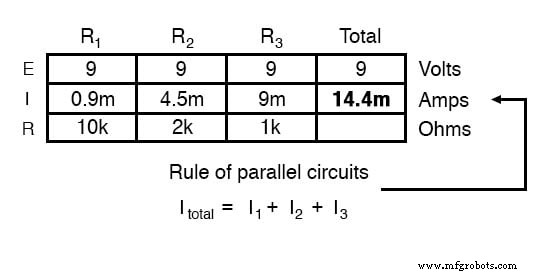
Cómo calcular la resistencia total en circuitos en paralelo

Finalmente, aplicando la ley de Ohm a la columna más a la derecha ("Total"), podemos calcular la resistencia total del circuito:

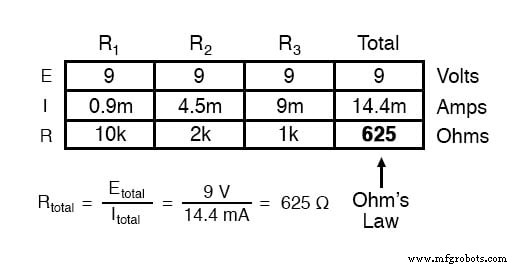
La ecuación para la resistencia en circuitos paralelos

Tenga en cuenta algo muy importante aquí. La resistencia total del circuito es de solo 625 Ω: menos que cualquiera de las resistencias individuales. En el circuito en serie, donde la resistencia total era la suma de las resistencias individuales, el total estaba destinado a ser mayor que cualquiera de las resistencias individualmente.

Aquí en el circuito paralelo, sin embargo, ocurre lo contrario:decimos que las resistencias individuales disminuir en lugar de agregar para hacer el total .

Este principio completa nuestra tríada de "reglas" para circuitos en paralelo, al igual que se descubrió que los circuitos en serie tienen tres reglas para voltaje, corriente y resistencia.

Matemáticamente, la relación entre la resistencia total y las resistencias individuales en un circuito paralelo se ve así:

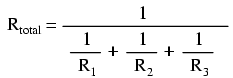
Cómo modificar los esquemas de numeración de circuitos paralelos para SPICE

La misma forma básica de la ecuación funciona para cualquier cantidad de resistencias conectadas entre sí en paralelo, simplemente agregue tantos términos 1 / R en el denominador de la fracción como sea necesario para acomodar todas las resistencias en paralelo en el circuito.

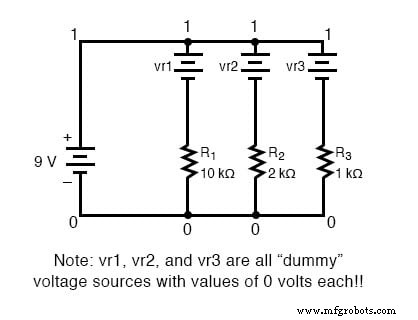
Al igual que con el circuito en serie, podemos usar el análisis por computadora para verificar nuestros cálculos. Primero, por supuesto, tenemos que describir nuestro circuito de ejemplo a la computadora en términos que pueda entender. Empezaré por volver a dibujar el circuito:

Una vez más, nos encontramos con que el esquema de numeración original utilizado para identificar puntos en el circuito tendrá que modificarse en beneficio de SPICE.

En SPICE, todos los puntos eléctricamente comunes deben compartir números de nodo idénticos. Así es como SPICE sabe qué está conectado con qué y cómo.

En un circuito paralelo simple, todos los puntos son eléctricamente comunes en uno de los dos conjuntos de puntos. Para nuestro circuito de ejemplo, el cable que conecta la parte superior de todos los componentes tendrá un número de nodo y el cable que conecta la parte inferior de los componentes tendrá el otro.

Manteniéndome fiel a la convención de incluir cero como número de nodo, elijo los números 0 y 1:

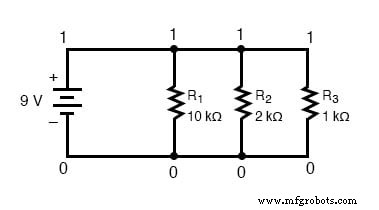
Un ejemplo como este hace que el fundamento de los números de nodo en SPICE sea bastante claro de entender. Al hacer que todos los componentes compartan conjuntos de números comunes, la computadora "sabe" que todos están conectados en paralelo entre sí.

Para mostrar las corrientes de derivación en SPICE, necesitamos insertar fuentes de voltaje cero en línea (en serie) con cada resistor, y luego hacer referencia a nuestras medidas de corriente a esas fuentes.

Por alguna razón, los creadores del programa SPICE hicieron que la corriente solo pudiera calcularse a través una fuente de voltaje. Esta es una demanda algo molesta del programa de simulación SPICE. Con cada una de estas fuentes de voltaje "ficticias" agregadas, se deben crear algunos números de nodo nuevos para conectarlos a sus respectivas resistencias de derivación:

Cómo verificar los resultados del análisis informático

Todas las fuentes de voltaje ficticias están configuradas a 0 voltios para no tener ningún impacto en el funcionamiento del circuito.

El archivo de descripción del circuito o netlist , tiene este aspecto:

 circuito paralelo v1 1 0 r1 2 0 10k r2 3 0 2k r3 4 0 1k vr1 1 2 dc 0 vr2 1 3 dc 0 vr3 1 4 dc 0 .dc v1 9 9 1 .print dc v (2,0) v (3,0) v (4,0) .imprimir dc yo (vr1) yo (vr2) yo (vr3) .fin 

Al ejecutar el análisis por computadora, obtenemos estos resultados (he anotado la impresión con etiquetas descriptivas):

v1 v (2) v (3) v (4) 9.000E + 009.000E + 009.000E + 009.000E + 00batería Tensión R1 Tensión R2 Tensión R3

Voltaje

v1 i (vr1) i (vr2) i (vr3) 9.000E + 009.000E-044.500E-039.000E-03 batería Corriente R1 Corriente R2 Corriente R3

Voltaje

De hecho, estos valores coinciden con los calculados anteriormente mediante la ley de Ohm:0,9 mA para I _R1 , 4,5 mA para I _R2 y 9 mA para I _R3 . Al estar conectados en paralelo, por supuesto, todas las resistencias tienen el mismo voltaje caído a través de ellas (9 voltios, igual que la batería).

Tres reglas de circuitos en paralelo

En resumen, un circuito paralelo se define como uno en el que todos los componentes están conectados entre el mismo conjunto de puntos eléctricamente comunes. Otra forma de decir esto es que todos los componentes están conectados a través de los terminales de los demás. De esta definición, se siguen tres reglas de circuitos paralelos:

• Todos los componentes comparten el mismo voltaje.
• Las resistencias disminuyen para igualar una resistencia total más pequeña.
• Las corrientes de rama se suman para igualar una corriente total mayor.

Al igual que en el caso de los circuitos en serie, todas estas reglas tienen su raíz en la definición de circuito en paralelo. Si comprende esa definición completamente, entonces las reglas no son más que notas al pie de la definición.

REVISAR:

• Los componentes de un circuito paralelo comparten el mismo voltaje:E _Total =E ₁ =E ₂ =. . . E _n
• La resistencia total en un circuito en paralelo es menor que cualquiera de las resistencias individuales:R _Total =1 / (1 / R ₁ + 1 / R ₂ +. . . 1 / R _n )
• La corriente total en un circuito en paralelo es igual a la suma de las corrientes de rama individuales:I _Total =I ₁ + I ₂ +. . . Yo _n .

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de práctica de circuitos de CC en paralelo con hoja de trabajo de respuestas
• Hoja de trabajo de manipulación de ecuaciones algebraicas para circuitos eléctricos