Circuitos computacionales

Cuando alguien menciona la palabra “computadora”, lo que generalmente viene a la mente es un dispositivo digital. Los circuitos digitales representan cantidades numéricas en binario formato:patrones de unos y ceros representados por una multitud de circuitos de transistores que operan en estados saturados o de corte. Sin embargo, los circuitos analógicos también se pueden usar para representar cantidades numéricas y realizar cálculos matemáticos, mediante el uso de señales de voltaje variable en lugar de estados discretos de encendido / apagado.

Aquí hay un ejemplo simple de representación binaria (digital) versus representación analógica del número "veinticinco":

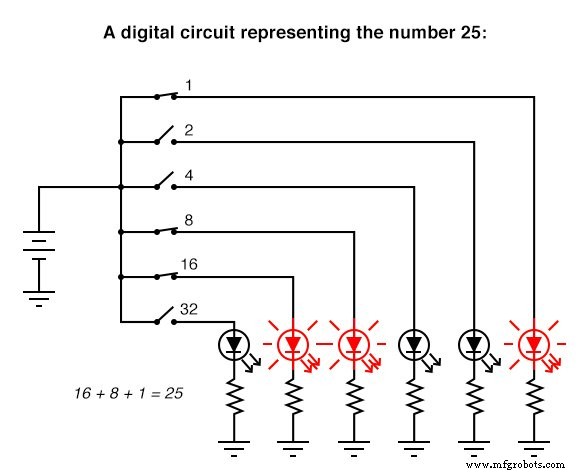
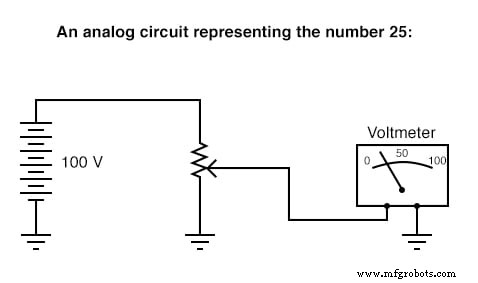
Los circuitos digitales son muy diferentes de los circuitos construidos sobre principios analógicos. Los circuitos computacionales digitales pueden ser increíblemente complejos, y los cálculos a menudo deben realizarse en "pasos" secuenciales para obtener una respuesta final, al igual que un ser humano realizaría cálculos aritméticos en pasos con lápiz y papel. Los circuitos computacionales analógicos, por otro lado, son bastante simples en comparación y realizan sus cálculos de manera continua y en tiempo real. Sin embargo, existe una desventaja en el uso de circuitos analógicos para representar números:la imprecisión. El circuito digital que se muestra arriba representa el número veinticinco, precisamente. El circuito analógico que se muestra arriba puede estar o no calibrado exactamente a 25.000 voltios, pero está sujeto a "desviaciones" y errores.

En aplicaciones donde la precisión no es crítica, los circuitos computacionales analógicos son muy prácticos y elegantes. Aquí se muestran algunos circuitos de amplificador operacional para realizar cálculos analógicos:

Circuitos de amplificador operacional computacional

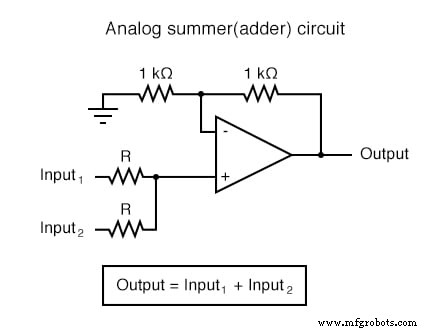
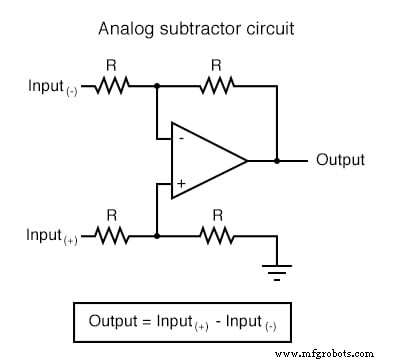
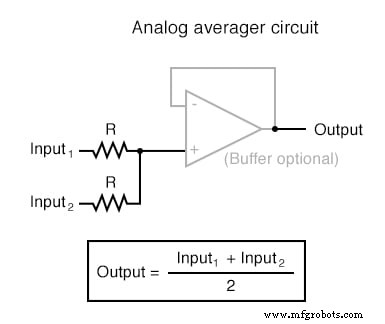
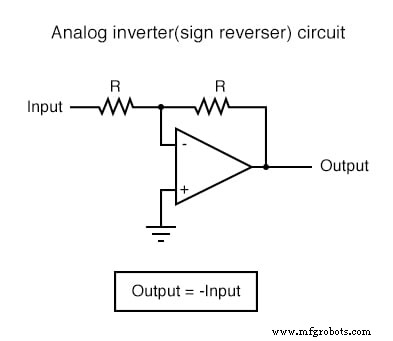
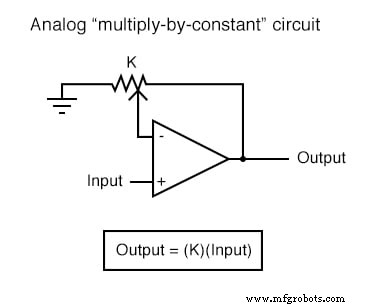
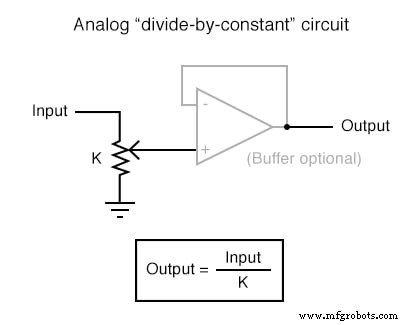
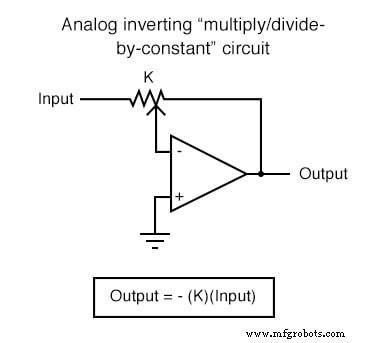
Cada uno de estos circuitos se puede utilizar de forma modular para crear un circuito capaz de realizar múltiples cálculos. Por ejemplo, suponga que necesitamos restar cierta fracción de una variable de otra variable. Combinando un circuito de división por constante con un circuito de resta, podríamos obtener la función requerida:

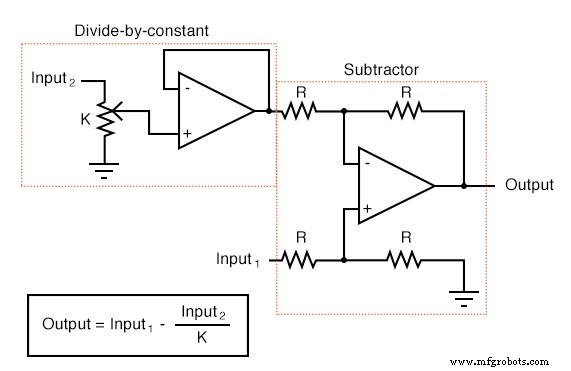
Dispositivos llamados computadoras analógicas solía ser común en universidades y talleres de ingeniería, donde decenas de circuitos de amplificadores operacionales se podían "parchear" junto con cables de puente extraíbles para modelar enunciados matemáticos, generalmente con el propósito de simular algún proceso físico cuyas ecuaciones subyacentes se conocían. Las computadoras digitales han hecho que las computadoras analógicas sean casi obsoletas, pero los circuitos computacionales analógicos no pueden ser superados por los digitales en términos de pura elegancia y economía de los componentes necesarios.

Los circuitos computacionales analógicos sobresalen en la realización de operaciones de cálculo integración y diferenciación con respecto al tiempo, mediante el uso de condensadores en un bucle de retroalimentación de amplificador operacional. Sin embargo, para comprender completamente el funcionamiento y las aplicaciones de estos circuitos, primero debemos comprender el significado de estos conceptos fundamentales de cálculo. Afortunadamente, la aplicación de circuitos de amplificador operacional a problemas del mundo real que involucran cálculo sirve como un medio excelente para enseñar cálculo básico. En palabras de John I. Smith, extraídas de su excelente libro de texto, Modern Operational Circuit Design :

“Se ofrece una nota de aliento a ciertos lectores:el cálculo integral es una de las disciplinas matemáticas que los circuitos operacionales [amplificadores] explotan y, en el proceso, más bien derriban como una barrera para la comprensión”. (pág. 4)

Los sentimientos del Sr. Smith sobre el valor pedagógico de los circuitos analógicos como herramienta de aprendizaje para las matemáticas no son únicos. Considere la opinión del ingeniero George Fox Lang, en un artículo que escribió para la edición de agosto de 2000 de la revista Sound and Vibration . , titulado "Analog era no ¡una marca comercial de computadora! ”:

“La creación de una entidad física real (un circuito) gobernada por un conjunto particular de ecuaciones e interactuar con él proporciona una visión única de esos enunciados matemáticos. No hay mejor manera de desarrollar una “intuición” de la interacción entre la física y las matemáticas que experimentar tal interacción. La computadora analógica fue una poderosa herramienta de enseñanza interdisciplinaria; Muchos educadores lamentan su obsolescencia en una variedad de campos ”. (pág. 23)

La diferenciación es la primera operación que típicamente aprenden los estudiantes principiantes de cálculo. En pocas palabras, la diferenciación determina la tasa de cambio instantánea de una variable en relación con otra. En los circuitos diferenciadores analógicos, la variable independiente es el tiempo, por lo que las tasas de cambio con las que estamos tratando son las tasas de cambio de una señal electrónica (voltaje o corriente) con respecto al tiempo.

Suponga que midiéramos la posición de un automóvil, viajando en una trayectoria directa (sin giros), desde su punto de partida. Llamemos a esta medida, x . Si el automóvil se mueve a una velocidad tal que su distancia desde el "inicio" aumenta de manera constante con el tiempo, su posición se trazará en un gráfico como un lineal función (línea recta):

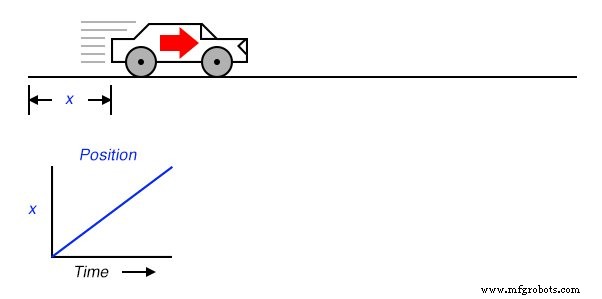
Si tuviéramos que calcular la derivada de la posición del automóvil con respecto al tiempo (es decir, determinar la tasa de cambio de la posición del automóvil con respecto al tiempo), llegaríamos a una cantidad que representa la velocidad del automóvil. La función de diferenciación está representada por la notación fraccionaria d / d , por lo que al diferenciar la posición ( x ) con respecto al tiempo ( t ), denotamos el resultado (la derivada) como dx / dt :

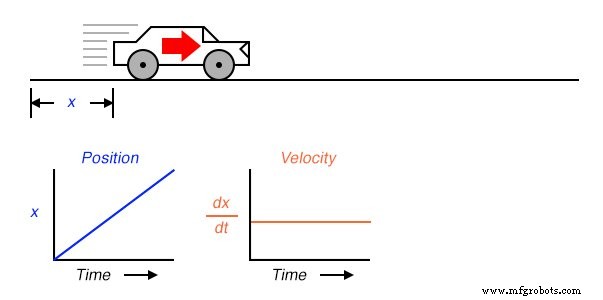
Para un gráfico lineal de x con el tiempo, la derivada de la posición ( dx / dt ), también conocido como velocidad , será una línea plana, cuyo valor no cambiará. La derivada de una función matemática puede entenderse gráficamente como su pendiente cuando se traza en un gráfico, y aquí podemos ver que la posición ( x ) tiene una pendiente constante, lo que significa que su derivada ( dx / dt ) debe ser constante en el tiempo.

Ahora, suponga que la distancia recorrida por el automóvil aumentó exponencialmente con el tiempo:es decir, comenzó su viaje con movimientos lentos, pero cubrió más distancia adicional con cada período de tiempo que pasa. Entonces veríamos que la derivada de la posición ( dx / dt ), también conocida como velocidad ( v ), no sería constante en el tiempo, pero aumentaría:

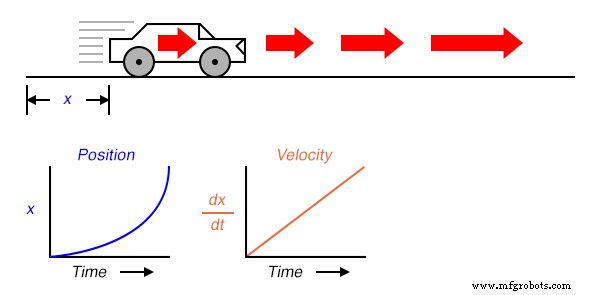
La altura de los puntos en el gráfico de velocidad corresponde a las tasas de cambio, o pendiente, de los puntos en los momentos correspondientes en el gráfico de posición:

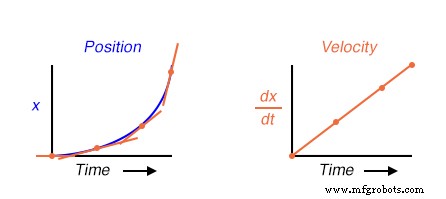
¿Qué tiene esto que ver con los circuitos electrónicos analógicos? Bueno, si tuviéramos que tener una señal de voltaje analógica que represente la posición del automóvil (piense en un enorme potenciómetro cuyo limpiaparabrisas estaba conectado al automóvil, generando un voltaje proporcional a la posición del automóvil), podríamos conectar un circuito diferenciador a esta señal y tener el circuito calcular continuamente la velocidad del automóvil, mostrando el resultado a través de un voltímetro conectado a la salida del circuito diferenciador:

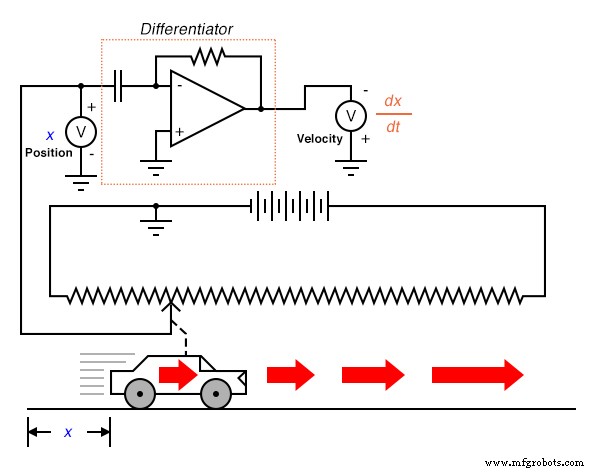
Recuerde del último capítulo que un circuito diferenciador genera un voltaje proporcional a la tasa de cambio en el tiempo del voltaje de entrada. ( d / dt ). Por lo tanto, si el voltaje de entrada cambia con el tiempo a una tasa constante , el voltaje de salida estará en un valor constante. Si el automóvil se mueve de tal manera que su distancia transcurrida a lo largo del tiempo se acumula a un ritmo constante, entonces eso significa que el automóvil viaja a una velocidad constante y el circuito del diferenciador generará un voltaje constante proporcional a esa velocidad. Si la distancia transcurrida del automóvil a lo largo del tiempo cambia de manera no constante, la salida del circuito diferenciador tampoco será estable, pero siempre a un nivel representativo de la tasa de cambio de la entrada a lo largo del tiempo.

Tenga en cuenta que el voltímetro que registra la velocidad (en la salida del circuito diferenciador) está conectado en polaridad "inversa" a la salida del amplificador operacional. Esto se debe a que el circuito diferenciador que se muestra está invertido :emitir un voltaje negativo para una tasa de cambio de voltaje de entrada positivo. Si deseamos que el voltímetro registre un valor positivo para la velocidad, tendrá que estar conectado al amplificador operacional como se muestra. Por poco práctico que sea conectar un potenciómetro gigante a un objeto en movimiento como un automóvil, el concepto debe ser claro:al realizar electrónicamente la función de cálculo de diferenciación en una señal que representa la posición, obtenemos una señal que representa la velocidad.

Los estudiantes principiantes de cálculo aprenden técnicas simbólicas para la diferenciación. Sin embargo, esto requiere que se conozca la ecuación que describe la gráfica original. Por ejemplo, los estudiantes de cálculo aprenden a tomar una función como y =3x y encontrar su derivada con respecto a x ( d / dx ), 3 , simplemente manipulando la ecuación. Podemos verificar la precisión de esta manipulación comparando los gráficos de las dos funciones:

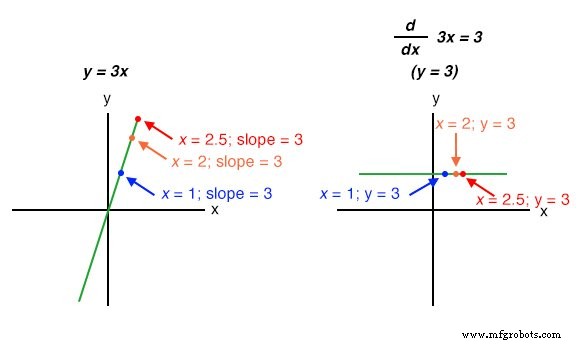
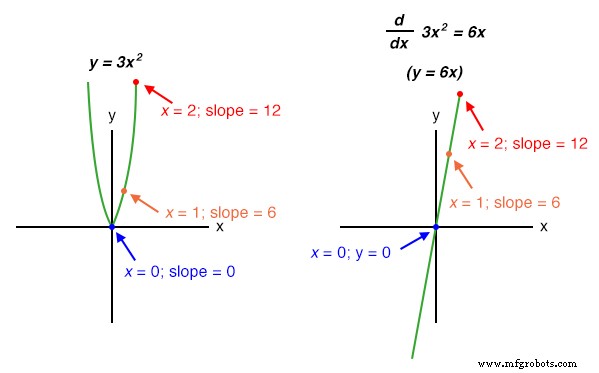
Funciones no lineales como y =3x ² también pueden diferenciarse por medios simbólicos. En este caso, la derivada de y =3x ² con respecto a x es 6x :

Sin embargo, en la vida real, a menudo no podemos describir el comportamiento de ningún evento físico mediante una ecuación simple como y =3x , por lo que la diferenciación simbólica del tipo aprendido por los estudiantes de cálculo puede ser imposible de aplicar a una medición física. Si alguien quisiera determinar la derivada de la posición de nuestro automóvil hipotético ( dx / dt =velocidad) por medios simbólicos, primero tendrían que obtener una ecuación que describa la posición del automóvil a lo largo del tiempo, basada en mediciones de posición tomadas de un experimento real; una tarea casi imposible a menos que el automóvil se opere bajo condiciones cuidadosamente controladas que conduzcan a una gráfico de posición. Sin embargo, un circuito diferenciador analógico, aprovechando el comportamiento de un capacitor con respecto al voltaje, la corriente y el tiempo i =C (dv / dt) , diferencia naturalmente cualquier señal real en relación con el tiempo, y podría generar una señal correspondiente a la velocidad instantánea ( dx / dt ) en cualquier momento. Al registrar la señal de posición del automóvil junto con la señal de salida del diferenciador utilizando un registrador de gráficos u otro dispositivo de adquisición de datos, ambos gráficos se presentarían naturalmente para su inspección y análisis.

Podemos llevar el principio de diferenciación un paso más allá aplicándolo a la señal de velocidad utilizando otro circuito diferenciador. En otras palabras, utilícelo para calcular la tasa de cambio de velocidad, que sabemos que es la tasa de cambio de posición. ¿A qué medida práctica llegaríamos si hiciéramos esto? Piense en esto en términos de las unidades que usamos para medir la posición y la velocidad. Si midiéramos la posición del automóvil desde su punto de partida en millas, probablemente expresaríamos su velocidad en unidades de millas por hora ( dx / dt ). Si tuviéramos que diferenciar la velocidad (medida en millas por hora) con respecto al tiempo, terminaríamos con una unidad de millas por hora por hora . Las clases de introducción a la física enseñan a los estudiantes sobre el comportamiento de la caída de objetos, midiendo la posición en metros , velocidad en metros por segundo y cambio de velocidad a lo largo del tiempo en metros por segundo, por segundo . Esta última medida se llama aceleración :la tasa de cambio de velocidad a lo largo del tiempo:

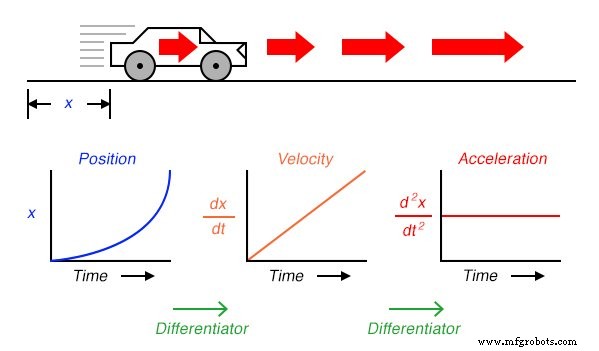
La expresión d ² x / dt ² se llama segunda derivada de posición ( x ) con respecto al tiempo ( t ). Si tuviéramos que conectar un segundo circuito diferenciador a la salida del primero, el último voltímetro registraría aceleración:

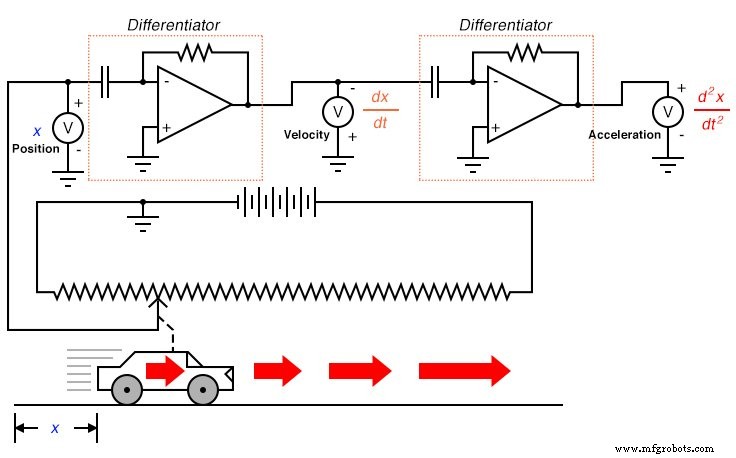
Derivando la velocidad de la posición y la aceleración de la velocidad, vemos el principio de diferenciación muy claramente ilustrado. Estas no son las únicas medidas físicas relacionadas entre sí de esta manera, pero son, quizás, las más comunes. Otro ejemplo de cálculo en acción es la relación entre el flujo de líquido ( q ) y volumen de líquido ( v ) acumulados en un recipiente a lo largo del tiempo:

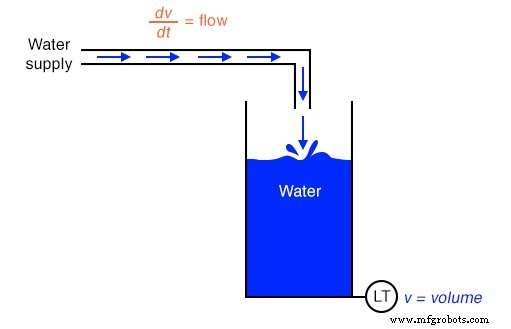
Un dispositivo "Transmisor de nivel" montado en un tanque de almacenamiento de agua proporciona una señal directamente proporcional al nivel del agua en el tanque, que, si el tanque tiene un área de sección transversal constante en toda su altura, equivale directamente al volumen de agua almacenado. Si tuviéramos que tomar esta señal de volumen y diferenciarla con respecto al tiempo ( dv / dt ), obtendríamos una señal proporcional al caudal del agua a través de la tubería que lleva el agua al tanque. Un circuito diferenciador conectado de tal manera que reciba esta señal de volumen produciría una señal de salida proporcional al flujo, posiblemente sustituyendo a un dispositivo de medición de flujo ("Transmisor de flujo") instalado en la tubería.

Volviendo al experimento del automóvil, suponga que nuestro automóvil hipotético estuviera equipado con un tacogenerador en una de las ruedas, produciendo una señal de voltaje directamente proporcional a la velocidad. Podríamos diferenciar la señal para obtener aceleración con un circuito, así:

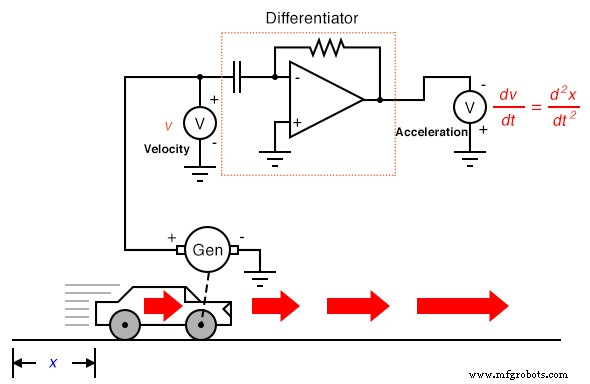
Por su propia naturaleza, el tacogenerador diferencia la posición del automóvil con respecto al tiempo, generando un voltaje proporcional a la rapidez con la que cambia la posición angular de la rueda con el tiempo. Esto nos proporciona una señal sin procesar que ya es representativa de la velocidad, con solo un paso de diferenciación necesario para obtener una señal de aceleración. Un tacogenerador que mide la velocidad, por supuesto, es un ejemplo mucho más práctico de instrumentación de automóvil que un potenciómetro gigante que mide su posición física, pero lo que ganamos en practicidad lo perdemos en la medición de posición. No importa cuántas veces diferenciamos, nunca podemos inferir la posición del automóvil a partir de una señal de velocidad. Si el proceso de diferenciación nos llevó de la posición a la velocidad y luego a la aceleración, entonces de alguna manera tenemos que realizar el proceso de diferenciación "inverso" para pasar de la velocidad a la posición. Tal proceso matemático existe, y se llama integración . El circuito "integrador" se puede utilizar para realizar esta función de integración con respecto al tiempo:

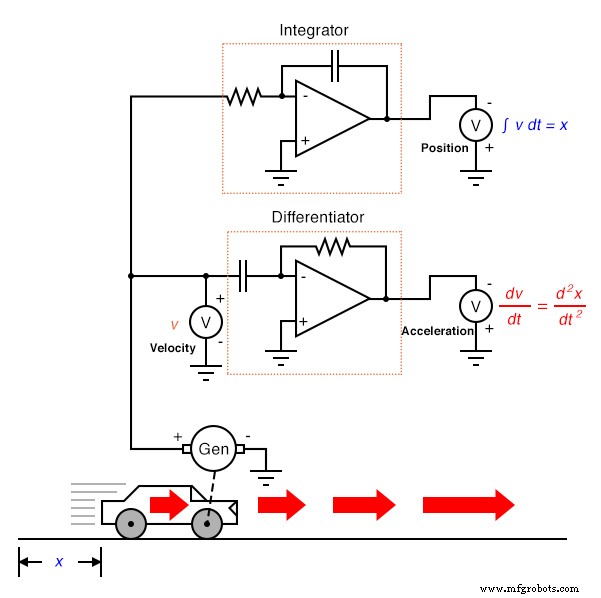
Recuerde del último capítulo que un circuito integrador genera un voltaje cuya tasa de cambio en el tiempo es proporcional a la magnitud del voltaje de entrada. Por lo tanto, dado un voltaje de entrada constante, el voltaje de salida cambiará a una tasa constante . Si el automóvil viaja a una velocidad constante (entrada de voltaje constante al circuito integrador desde el tacogenerador), entonces su distancia recorrida aumentará constantemente a medida que avanza el tiempo, y el integrador generará un voltaje que cambia constantemente proporcional a esa distancia. Si la velocidad del automóvil no es constante, la tasa de cambio a lo largo del tiempo tampoco será la salida del circuito integrador, pero el voltaje de salida lo hará representar fielmente la cantidad de distancia recorrida por el automóvil en un momento dado.

El símbolo de integración se parece a una letra cursiva muy estrecha "S" (∫). La ecuación que utiliza este símbolo (∫ v dt =x ) nos dice que estamos integrando velocidad ( v ) con respecto al tiempo ( dt ) y obtener la posición ( x ) como resultado.

Entonces, podemos expresar tres medidas del movimiento del automóvil (posición, velocidad y aceleración) en términos de velocidad ( v ) tan fácilmente como podríamos en términos de posición ( x ):

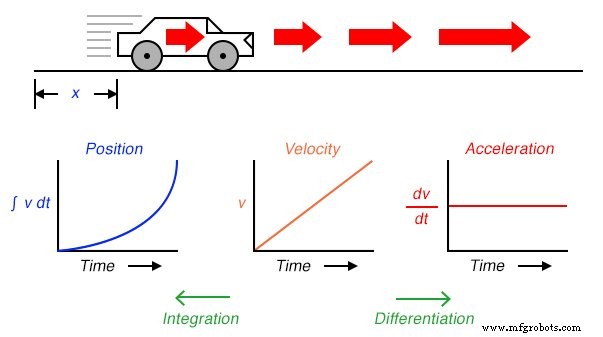
Si tuviéramos un acelerómetro conectado al automóvil, generando una señal proporcional a la tasa de aceleración o desaceleración, podríamos (hipotéticamente) obtener una señal de velocidad con un paso de integración y una señal de posición con un segundo paso de integración:

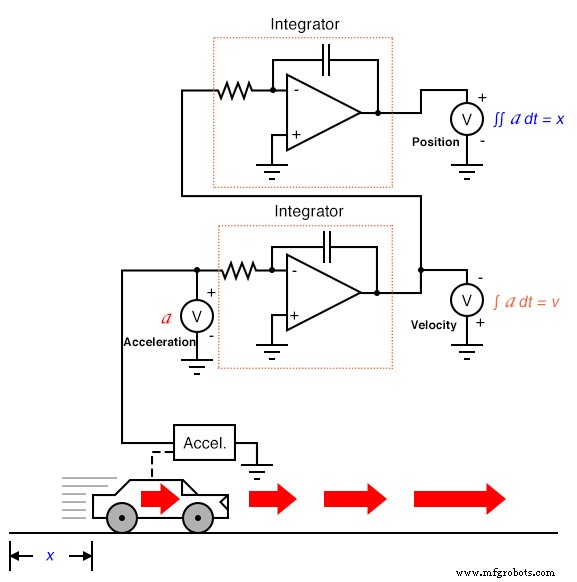
Por lo tanto, las tres medidas del movimiento del automóvil (posición, velocidad y aceleración) pueden expresarse en términos de aceleración:

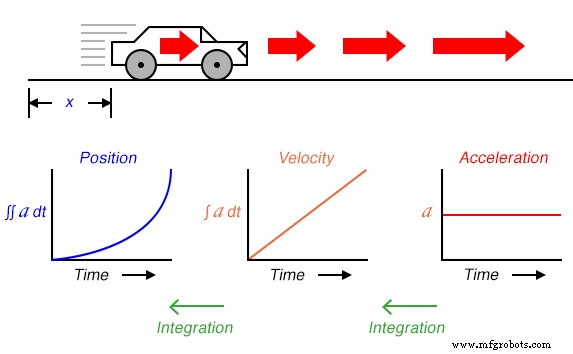
Como puede haber sospechado, el proceso de integración también puede ilustrarse y aplicarse a otros sistemas físicos. Tomemos, por ejemplo, el tanque de almacenamiento de agua y el ejemplo de flujo que se mostró anteriormente. Si el caudal es el derivado del volumen del tanque con respecto al tiempo ( q =dv / dt ), entonces también podríamos decir que el volumen es la integral de caudal con respecto al tiempo:

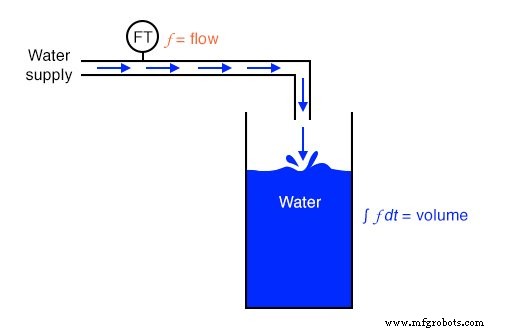
Si tuviéramos que usar un dispositivo "Transmisor de flujo" para medir el flujo de agua, entonces mediante la integración del tiempo podríamos calcular el volumen de agua acumulado en el tanque a lo largo del tiempo. Aunque teóricamente es posible utilizar un circuito integrador de amplificador operacional capacitivo para derivar una señal de volumen a partir de una señal de flujo, los dispositivos "integradores" electrónicos mecánicos y digitales son más adecuados para la integración durante largos períodos de tiempo y encuentran un uso frecuente en el agua. industrias de tratamiento y distribución.

Así como existen técnicas simbólicas de diferenciación, también existen técnicas simbólicas de integración, aunque tienden a ser más complejas y variadas. Sin embargo, aplicar la integración simbólica a un problema del mundo real como la aceleración de un automóvil aún depende de la disponibilidad de una ecuación que describa con precisión la señal medida, a menudo una cosa difícil o imposible de derivar de los datos medidos. Sin embargo, los circuitos integradores electrónicos realizan esta función matemática de forma continua, en tiempo real y para cualquier perfil de señal de entrada, lo que proporciona una herramienta poderosa para científicos e ingenieros.

Habiendo dicho esto, existen salvedades sobre el uso de técnicas de cálculo para derivar un tipo de medición de otro. La diferenciación tiene la tendencia indeseable de amplificar el "ruido" que se encuentra en la variable medida, ya que el ruido aparecerá típicamente como frecuencias mucho más altas que la variable medida, y las altas frecuencias por su propia naturaleza poseen altas tasas de cambio a lo largo del tiempo.

Para ilustrar este problema, suponga que derivamos una medida de la aceleración del automóvil a partir de la señal de velocidad obtenida de un tacogenerador con escobillas gastadas o barras de conmutación. Los puntos de contacto deficiente entre la escobilla y el conmutador producirán "caídas" momentáneas en el voltaje de salida del tacogenerador, y el circuito diferenciador conectado a él interpretará estas caídas como cambios muy rápidos de velocidad. Para un automóvil que se mueve a velocidad constante, ni acelerando ni desacelerando, la señal de aceleración debe ser de 0 voltios, pero el "ruido" en la señal de velocidad causado por un tacogenerador defectuoso hará que la señal diferenciada (aceleración) contenga "picos", lo que indica falsamente breves períodos de alta aceleración y desaceleración:

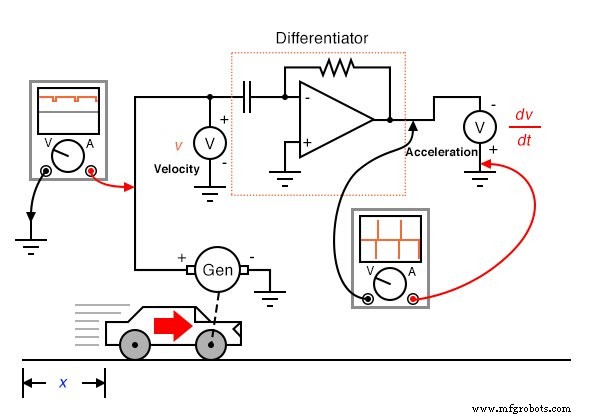
El voltaje de ruido presente en una señal a diferenciar no necesita ser de amplitud significativa para causar problemas:todo lo que se requiere es que el perfil de ruido tenga tiempos de subida o bajada rápidos. En otras palabras, cualquier ruido eléctrico con un dv / dt alto El componente será problemático cuando se diferencia, incluso si es de baja amplitud.

Cabe señalar que este problema no es un artefacto (un error idiosincrásico del instrumento de medición / computación) de los circuitos analógicos; más bien, es inherente al proceso de diferenciación. No importa cómo realicemos la diferenciación, el "ruido" en la señal de velocidad dañará invariablemente la señal de salida. Por supuesto, si diferenciamos una señal dos veces, como hicimos para obtener tanto la velocidad como la aceleración de una señal de posición, la salida de la señal de ruido amplificada por el primer circuito diferenciador será amplificada nuevamente por el siguiente diferenciador, agravando así el problema:

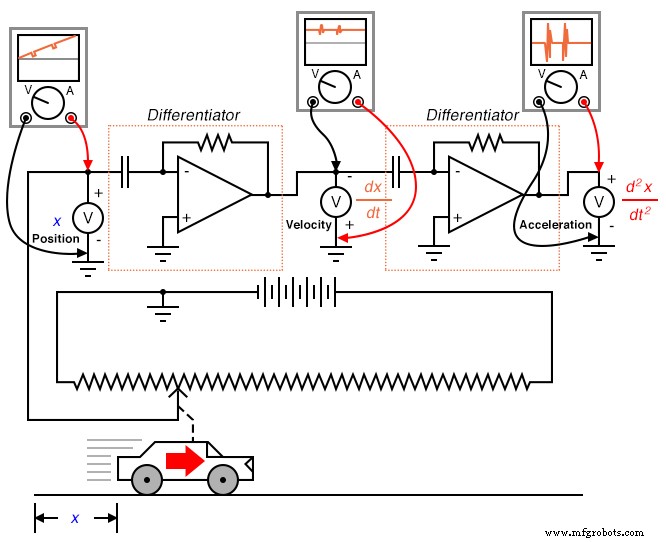
La integración no sufre este problema, porque los integradores actúan como filtros de paso bajo, atenuando las señales de entrada de alta frecuencia. En efecto, todos los picos altos y bajos resultantes del ruido en la señal se promedian juntos con el tiempo, para un resultado neto disminuido. Se podría suponer, entonces, que podríamos evitar todos los problemas midiendo la aceleración directamente e integrando esa señal para obtener la velocidad; en efecto, calculando "a la inversa" de la forma mostrada anteriormente:

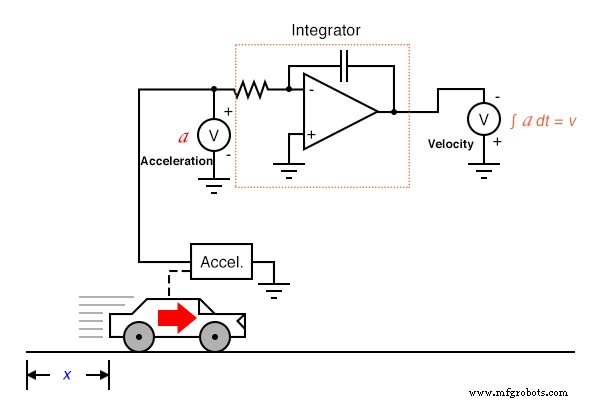
Desafortunadamente, seguir esta metodología podría llevarnos a otras dificultades, una de las cuales es un artefacto común de los circuitos integradores analógicos conocido como deriva . Todos los amplificadores operacionales tienen cierta cantidad de corriente de polarización de entrada, y esta corriente tenderá a hacer que se acumule una carga en el capacitor además de cualquier carga que se acumule como resultado de la señal de voltaje de entrada. En otras palabras, todos los circuitos integradores analógicos sufren la tendencia de tener su voltaje de salida "deriva" o "deslizamiento" incluso cuando no hay absolutamente ninguna entrada de voltaje, acumulando como resultado un error a lo largo del tiempo. Además, los capacitores imperfectos tenderán a perder su carga almacenada con el tiempo debido a la resistencia interna, lo que resultará en una "deriva" hacia un voltaje de salida cero. Estos problemas son artefactos de los circuitos analógicos y pueden eliminarse mediante el uso de computación digital.

A pesar de los artefactos del circuito, los posibles errores pueden resultar de la integración de una medición (como la aceleración) para obtener otra (como la velocidad) simplemente debido a la forma en que funciona la integración. Si el punto de calibración "cero" del sensor de señal sin procesar no es perfecto, emitirá una señal levemente positiva o negativa incluso en condiciones en las que no debería emitir nada. Considere un automóvil con un acelerómetro calibrado de manera imperfecta, o uno que está influenciado por la gravedad para detectar una ligera aceleración no relacionada con el movimiento del automóvil. Incluso con una computadora de integración perfecta, este error del sensor hará que el integrador acumule errores, lo que dará como resultado una señal de salida que indica un cambio de velocidad cuando el automóvil no está acelerando ni desacelerando.

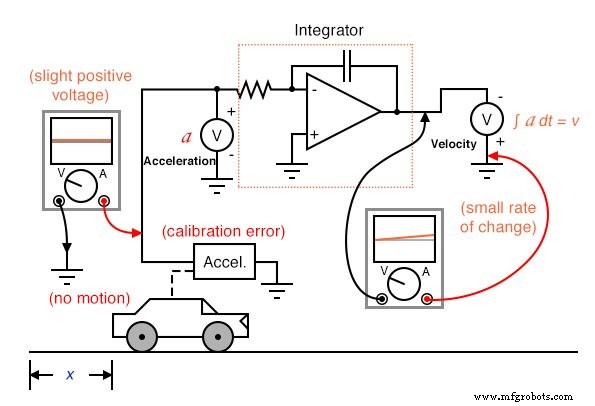
Al igual que con la diferenciación, este error también se agravará si la señal integrada se pasa a otro circuito integrador, ya que la salida "derivada" del primer integrador muy pronto presentará una señal significativa positiva o negativa para que el próximo integrador la integre. Por lo tanto, se debe tener cuidado al integrar las señales del sensor:si el ajuste "cero" del sensor no es perfecto , el resultado integrado se desviará, incluso si el circuito integrador en sí es perfecto.

Hasta ahora, los únicos errores de integración discutidos han sido de naturaleza artificial:originados por imperfecciones en los circuitos y sensores. También existe una fuente de error inherente al propio proceso de integración, y esa es la constante desconocida problema. Los estudiantes principiantes de cálculo aprenden que siempre que se integra una función, existe una constante desconocida (generalmente representada como la variable C ) añadido al resultado. Esta incertidumbre es más fácil de entender comparando las derivadas de varias funciones que difieren solo por la adición de un valor constante:

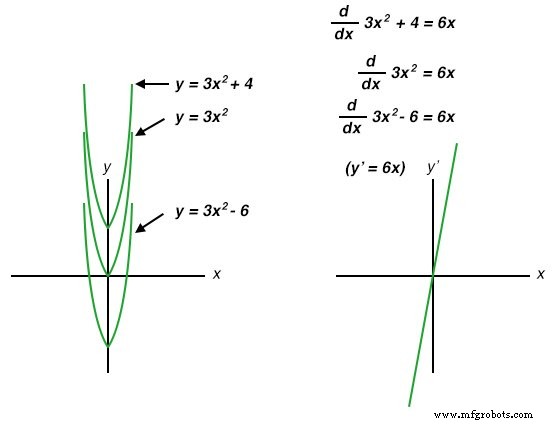
Observe cómo cada una de las curvas parabólicas ( y =3x ² + C ) comparten exactamente la misma forma, diferenciándose entre sí en cuanto a su desplazamiento vertical. Sin embargo, todos comparten exactamente la misma función derivada: y ’=(d / dx) (3x ² + C) =6x , porque todos comparten tasas de cambio idénticas (pendientes) en los puntos correspondientes a lo largo de la x eje. Si bien esto parece bastante natural y esperado desde la perspectiva de la diferenciación (diferentes ecuaciones que comparten una derivada común), generalmente a los estudiantes principiantes les parece extraño desde la perspectiva de la integración, porque hay múltiples respuestas correctas para la integral de una función. Al pasar de una ecuación a su derivada, solo hay una respuesta, pero volver de esa derivada a la ecuación original nos lleva a un rango de soluciones correctas. En honor a esta incertidumbre, la función simbólica de la integración se llama integral indefinida .

Cuando un integrador realiza la integración de señales en vivo con respecto al tiempo, la salida es la suma de la señal de entrada integrada a lo largo del tiempo y un valor inicial de magnitud arbitraria, que representa la salida preexistente del integrador en el momento en que comenzó la integración. Por ejemplo, si integro la velocidad de un automóvil que se conduce en línea recta desde una ciudad, calculando que una velocidad constante de 50 millas por hora durante un tiempo de 2 horas producirá una distancia (∫ v dt ) de 100 millas, eso no significa necesariamente que el automóvil estará a 100 millas de la ciudad después de 2 horas. Todo lo que nos dice es que el auto estará a 100 millas más lejos de la ciudad después de 2 horas de conducción. La distancia real desde la ciudad después de 2 horas de conducción depende de qué tan lejos estaba el automóvil de la ciudad cuando comenzó la integración. Si no conocemos este valor inicial para la distancia, no podemos determinar la distancia exacta del automóvil desde la ciudad después de 2 horas de conducción.

Este mismo problema aparece cuando integramos la aceleración con respecto al tiempo para obtener la velocidad:

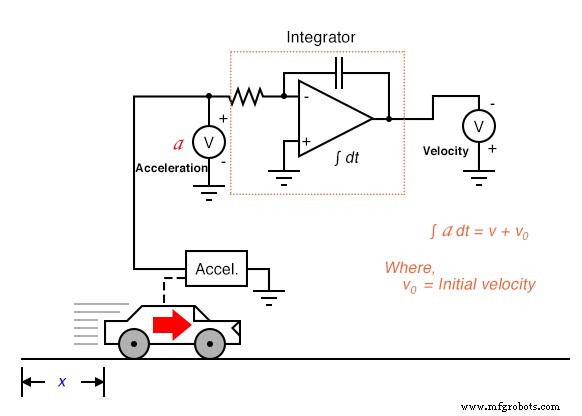
En este sistema integrador, la velocidad calculada del automóvil solo será válida si el circuito integrador está inicializado a un valor de salida de cero cuando el automóvil está parado ( v =0). De lo contrario, el integrador podría estar generando una señal distinta de cero para la velocidad ( v ₀ ) cuando el automóvil está parado, ya que el acelerómetro no puede diferenciar entre un estado estacionario (0 millas por hora) y un estado de velocidad constante (digamos, 60 millas por hora, sin cambios). Esta incertidumbre en la salida del integrador es inherente al proceso de integración y no un artefacto del circuito o del sensor.

En resumen, si se desea la máxima precisión para cualquier medición física, es mejor medir esa variable directamente en lugar de calcularla a partir de otras mediciones. Esto no quiere decir que el cálculo sea inútil. Muy al contrario, a menudo es el único medio práctico de obtener la medida deseada. Sin embargo, los límites del cálculo deben entenderse y respetarse para que se obtengan medidas precisas.

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de circuitos computacionales lineales