Circuitos complejos
¿Qué hacemos si nos encontramos con un circuito más complejo que las configuraciones en serie simples que hemos visto hasta ahora? Tome este circuito como ejemplo:
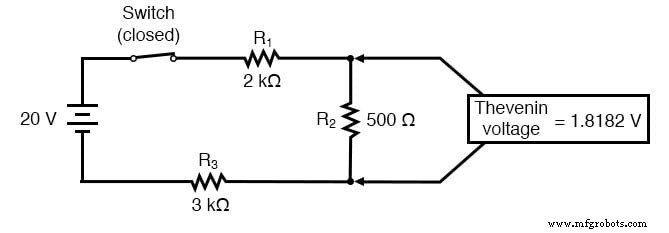
La fórmula de constante de tiempo simple (τ =RC) se basa en una resistencia en serie simple conectada al capacitor. Para el caso, la fórmula de la constante de tiempo para un circuito inductivo (τ =L / R) también se basa en el supuesto de una resistencia en serie simple. Entonces, ¿qué podemos hacer en una situación como esta, donde las resistencias están conectadas en serie en paralelo con el capacitor (o inductor)?
Teorema de Thevenin
La respuesta proviene de nuestros estudios en análisis de redes. El teorema de Thevenin nos dice que podemos reducir cualquier circuito lineal a un equivalente de una fuente de voltaje, una resistencia en serie y un componente de carga a través de un par de pasos simples. Para aplicar el teorema de Thevenin a nuestro escenario aquí, consideraremos el componente reactivo (en el circuito de ejemplo anterior, el capacitor) como la carga y lo retiraremos temporalmente del circuito para encontrar el voltaje de Thevenin y la resistencia de Thevenin.
Luego, una vez que hayamos determinado los valores del circuito equivalente de Thevenin, volveremos a conectar el capacitor y resolveremos los valores de voltaje o corriente a lo largo del tiempo, como lo hemos estado haciendo hasta ahora.
Después de identificar el capacitor como la "carga", lo retiramos del circuito y resolvemos el voltaje a través de los terminales de carga (asumiendo, por supuesto, que el interruptor está cerrado):

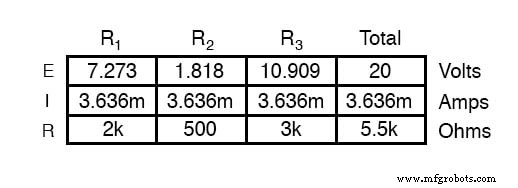
Este paso del análisis nos dice que el voltaje en los terminales de carga (el mismo que en el resistor R 2 ) será de 1.8182 voltios sin carga conectada. Con un poco de reflexión, debería quedar claro que este será nuestro voltaje final a través del capacitor, ya que un capacitor completamente cargado actúa como un circuito abierto, consumiendo corriente cero. Usaremos este valor de voltaje para nuestro voltaje de fuente de circuito equivalente de Thevenin.
Ahora, para resolver nuestra resistencia de Thevenin, necesitamos eliminar todas las fuentes de energía en el circuito original y calcular la resistencia como se ve desde los terminales de carga:
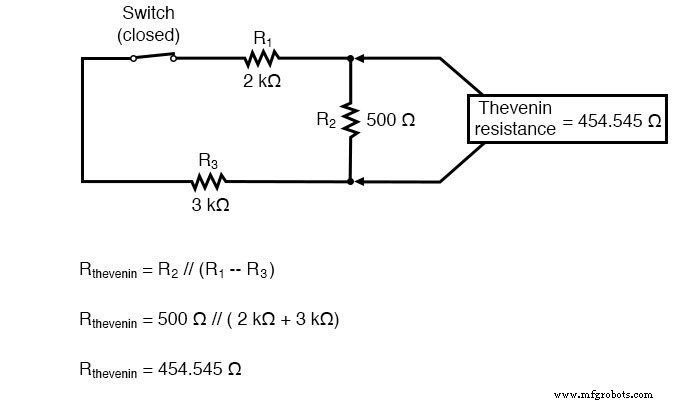
Al volver a dibujar nuestro circuito como un equivalente de Thevenin, obtenemos esto:
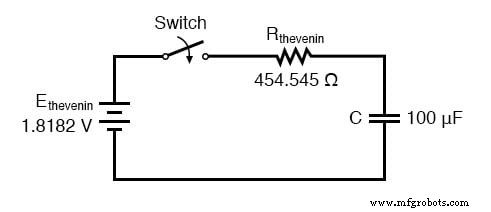
Nuestra constante de tiempo para este circuito será igual a la resistencia de Thevenin multiplicada por la capacitancia (τ =RC). Con los valores anteriores, calculamos:

Ahora, podemos resolver el voltaje a través del capacitor directamente con nuestra fórmula de constante de tiempo universal. Calculemos un valor de 60 milisegundos. Debido a que esta es una fórmula capacitiva, configuraremos nuestros cálculos para voltaje:

Nuevamente, debido a que se asumió que nuestro valor inicial para el voltaje del capacitor era cero, el voltaje real a través del capacitor a 60 milisegundos es igual a la cantidad de cambio de voltaje desde cero, o 1.3325 voltios.
Podríamos ir un paso más allá y demostrar la equivalencia del circuito Thevenin RC y el circuito original a través del análisis por computadora. Usaré el programa de análisis SPICE para demostrar esto:
Análisis de RC de comparación * primero, la lista de conexiones del circuito original:v1 1 0 dc 20 r1 1 2 2k r2 2 3500 r3 3 0 3k c1 2 3 100u ic =0 * luego, la lista de conexiones para el equivalente de thevenin:v2 4 0 dc 1.818182 r4 4 5 454,545 c2 5 0 100u ic =0 * ahora, analizamos por un transitorio, muestreando cada .005 segundos * durante un período de tiempo de 0,37 segundos en total, imprimiendo una lista de * valores de voltaje a través del condensador en el original * circuito (entre los modos 2 y 3) y a través del condensador en * el circuito equivalente de Thevenin (entre los nodos 5 y 0) .tran .005 0.37 uic .print tran v (2,3) v (5,0) .fin
Que se imprime como:
En cada paso del proceso de análisis, los condensadores de los dos circuitos (circuito original versus circuito equivalente de Thevenin) tienen el mismo voltaje, lo que demuestra la equivalencia de los dos circuitos.
REVISAR:
- Para analizar un circuito RC o L / R más complejo que una serie simple, convierta el circuito en un equivalente de Thevenin tratando el componente reactivo (capacitor o inductor) como la "carga" y reduciendo todo lo demás a un circuito equivalente de uno fuente de voltaje y una resistencia en serie. Luego, analice lo que sucede a lo largo del tiempo con la fórmula de la constante de tiempo universal.
HOJAS DE TRABAJO RELACIONADAS:
- Hoja de trabajo de los teoremas de transferencia de potencia máxima de Thevenin, Norton y
Tecnología Industrial
- Ecuaciones del circuito de CA
- Circuitos de control del motor
- Uso de múltiples circuitos combinacionales
- Circuitos amplificadores
- Circuitos de radio
- Circuitos de control
- ¿Qué son los circuitos eléctricos?
- Simulación por computadora de circuitos eléctricos
- ¿Qué son los circuitos en “serie” y “paralelo”?
- Resonancia en circuitos en serie-paralelo
- Introducción a los diferentes circuitos hidráulicos



