Resonancia en circuitos en serie-paralelo

En circuitos reactivos simples con poca o ninguna resistencia, los efectos de la impedancia radicalmente alterada se manifestarán en la frecuencia de resonancia predicha por la ecuación dada anteriormente. En un circuito LC paralelo (tanque), esto significa impedancia infinita en resonancia. En un circuito LC en serie, significa impedancia cero en resonancia:

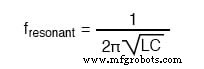
Sin embargo, tan pronto como se introducen niveles significativos de resistencia en la mayoría de los circuitos LC, este simple cálculo de resonancia deja de ser válido.

En esta página, veremos varios circuitos LC con resistencia adicional, utilizando los mismos valores de capacitancia e inductancia que antes:10 µF y 100 mH, respectivamente.

Cálculo de la frecuencia de resonancia de un circuito de alta resistencia

Según nuestra sencilla ecuación anterior, la frecuencia de resonancia debería ser de 159,155 Hz. Sin embargo, observe dónde la corriente alcanza el máximo o el mínimo en los siguientes análisis de SPICE:

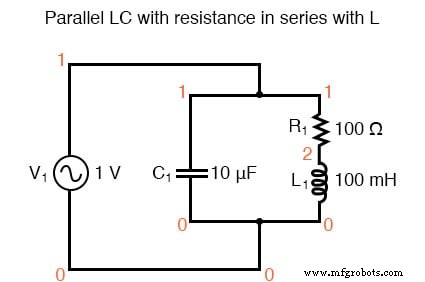
Circuito LC paralelo con resistencia en serie con L.

 circuito resonante v1 1 0 ac 1 pecado c1 1 0 10u r1 1 2 100 l1 2 0 100m .ac lin 20100200 .plot ac i (v1) .fin 

Resultados:

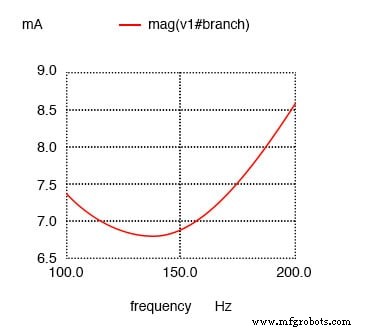
La resistencia en serie con L produce una corriente mínima a 136,8 Hz en lugar de los 159,2 Hz calculados

 ¡Corriente mínima a 136,8 Hz en lugar de 159,2 Hz! 

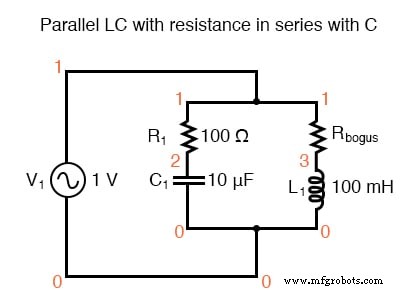
LC paralelo con resistencia en serie con C.

Aquí, es necesaria una resistencia adicional (Rbogus) para evitar que SPICE encuentre problemas en el análisis. SPICE no puede manejar un inductor conectado directamente en paralelo con ninguna fuente de voltaje o cualquier otro inductor, por lo que es necesario agregar una resistencia en serie para "romper" la fuente de voltaje / bucle del inductor que de otro modo se formaría.

Esta resistencia se elige para ser muy valor bajo para un impacto mínimo en el comportamiento del circuito.

 circuito resonante v1 1 0 ac 1 pecado r1 1 2 100 c1 2 0 10u rbogus 1 3 1e-12 l1 3 0 100m .ac lin 20100 400 .plot ac i (v1) .fin 

 ¡Corriente mínima a aproximadamente 180 Hz en lugar de 159,2 Hz! 

Resultados:

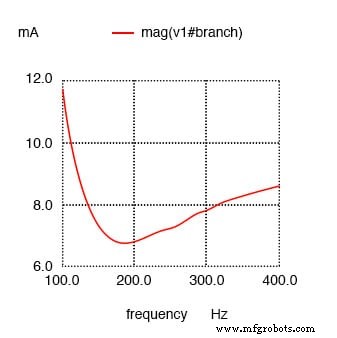
La resistencia en serie con C cambia la corriente mínima de 159,2 Hz calculados a aproximadamente 180 Hz.

Circuitos LC en serie

Cambiando nuestra atención a los circuitos LC en serie, experimentamos colocando resistencias significativas en paralelo con L o C. En los siguientes ejemplos de circuitos en serie, se coloca una resistencia de 1 Ω (R1) en serie con el inductor y el condensador para limitar la corriente total en resonancia.

La resistencia "extra" insertada para influir en los efectos de la frecuencia resonante es la resistencia de 100 Ω, R2. Los resultados se muestran en la siguiente figura.

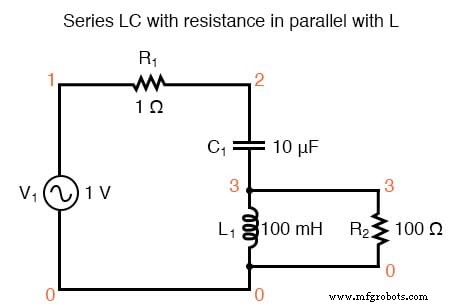
Circuito resonante LC serie con resistencia en paralelo con L.

 circuito resonante v1 1 0 ac 1 pecado r1 1 2 1 c1 2 3 10u l1 3 0 100m r2 3 0100 .ac lin 20100 400 .plot ac i (v1) .fin 

 ¡Corriente máxima a aproximadamente 178,9 Hz en lugar de 159,2 Hz! 

Resultados:

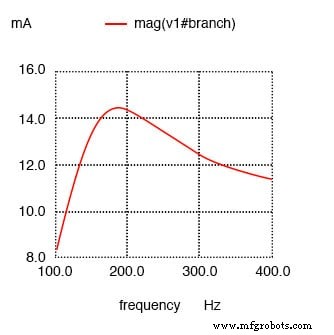
El circuito resonante en serie con resistencia en paralelo con L cambia la corriente máxima de 159,2 Hz a aproximadamente 180 Hz.

Y finalmente, un circuito LC en serie con la resistencia significativa en paralelo con el capacitor. La resonancia desplazada se muestra a continuación.

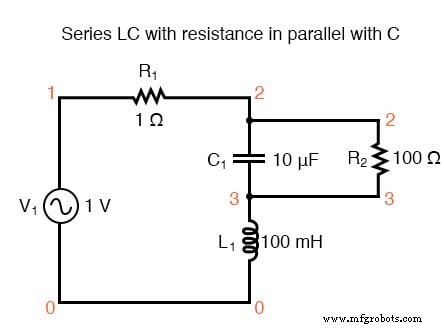
Circuito resonante LC serie con resistencia en paralelo con C.

 circuito resonante v1 1 0 ac 1 pecado r1 1 2 1 c1 2 3 10u r2 2 3100 l1 3 0 100m .ac lin 20100200 .plot ac i (v1) .fin 

 ¡Corriente máxima a 136,8 Hz en lugar de 159,2 Hz! 

Resultados:

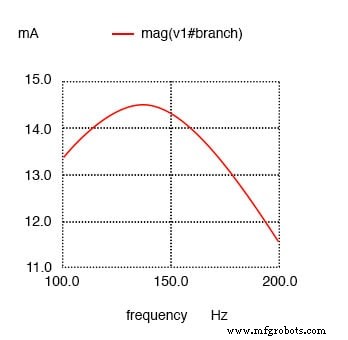
La resistencia en paralelo con C en el circuito resonante en serie cambia la corriente máxima de 159,2 Hz calculados a aproximadamente 136,8 Hz.

Antirresonancia en circuitos LC

La tendencia de la resistencia adicional a sesgar el punto en el que la impedancia alcanza un máximo o un mínimo en un circuito LC se denomina antirresonancia . El observador astuto notará un patrón entre los cuatro ejemplos de SPICE dados anteriormente, en términos de cómo la resistencia afecta el pico resonante de un circuito:

Circuito LC paralelo ("tanque"):

• R en serie con L:frecuencia de resonancia desplazada hacia abajo
• R en serie con C:frecuencia de resonancia desplazada hacia arriba

Circuito LC en serie:

• R en paralelo con L:frecuencia de resonancia desplazada hacia arriba
• R en paralelo con C:frecuencia de resonancia desplazada hacia abajo

Nuevamente, esto ilustra la naturaleza complementaria de los capacitores y los inductores:cómo la resistencia en serie con uno crea un efecto antirresonancia equivalente a la resistencia en paralelo con el otro. Si observa aún más de cerca los cuatro ejemplos de SPICE dados, verá que las frecuencias se desplazan en la misma cantidad , ¡y que la forma de los gráficos complementarios son imágenes especulares entre sí!

Antirresonancia es un efecto que los diseñadores de circuitos resonantes deben conocer. Las ecuaciones para determinar el “cambio” de antirresonancia son complejas y no se tratarán en esta breve lección. Debería ser suficiente para el estudiante principiante de electrónica comprender que el efecto existe y cuáles son sus tendencias generales.

El efecto piel

La resistencia adicional en un circuito LC no es un asunto académico. Si bien es posible fabricar condensadores con resistencias no deseadas insignificantes, los inductores suelen estar plagados de cantidades sustanciales de resistencia debido a las grandes longitudes de cable que se utilizan en su construcción.

Además, la resistencia del cable tiende a aumentar a medida que aumenta la frecuencia, debido a un extraño fenómeno conocido como efecto piel donde la corriente CA tiende a excluirse del viaje a través del centro mismo de un cable, lo que reduce el área de sección transversal efectiva del cable.

Por lo tanto, los inductores no solo tienen resistencia, sino que también cambian, dependientes de la frecuencia resistencia en eso.

Resistencia agregada en circuitos

Como si la resistencia del cable de un inductor no fuera suficiente para causar problemas, también tenemos que lidiar con las "pérdidas del núcleo" de los inductores de núcleo de hierro, que se manifiestan como una resistencia adicional en el circuito.

Dado que el hierro es un conductor de electricidad y un conductor de flujo magnético, el flujo cambiante producido por la corriente alterna a través de la bobina tenderá a inducir corrientes eléctricas en el núcleo mismo ( corrientes parásitas ). ).

Se puede pensar en este efecto como si el núcleo de hierro del transformador fuera una especie de bobina de transformador secundario que alimenta una carga resistiva:la conductividad menos que perfecta del metal de hierro. Estos efectos se pueden minimizar con núcleos laminados, materiales de alta calidad de buen diseño de núcleos, pero nunca se eliminan por completo.

Circuitos RLC

Una excepción notable a la regla de la resistencia del circuito que causa un cambio de frecuencia resonante es el caso de los circuitos en serie resistor-inductor-capacitor (“RLC”). Siempre que todos Los componentes están conectados en serie entre sí, la frecuencia de resonancia del circuito no se verá afectada por la resistencia. El gráfico resultante se muestra a continuación.

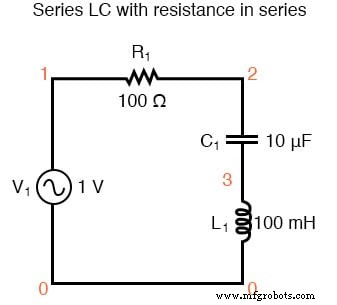
Serie LC con resistencia en serie.

 circuito rlc en serie v1 1 0 ac 1 pecado r1 1 2 100 c1 2 3 10u l1 3 0 100m .ac lin 20100200 .plot ac i (v1) .fin 

 ¡Corriente máxima a 159,2 Hz una vez más! 

Resultados:

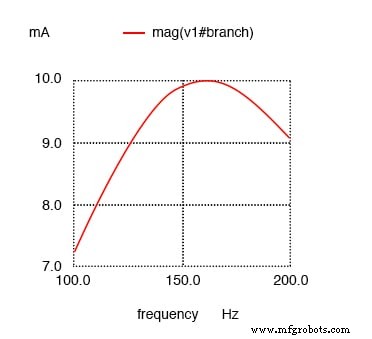
La resistencia en el circuito resonante en serie deja el máximo de corriente en 159,2 Hz calculados, lo que amplía la curva.

Tenga en cuenta que el pico del gráfico de corriente no ha cambiado con respecto al circuito LC de la serie anterior (el que tiene la resistencia simbólica de 1 Ω), aunque la resistencia ahora es 100 veces mayor. Lo único que ha cambiado es la "nitidez" de la curva.

Obviamente, este circuito no resuena con tanta fuerza como uno con menos resistencia en serie (se dice que es "menos selectivo"), ¡pero al menos tiene la misma frecuencia natural!

Efecto amortiguador de la antiresonancia

Cabe señalar que la antiresonancia tiene el efecto de amortiguar las oscilaciones de los circuitos LC de funcionamiento libre, como los circuitos de tanque. Al comienzo de este capítulo, vimos cómo un capacitor y un inductor conectados directamente juntos actuarían como un péndulo, intercambiando picos de voltaje y corriente al igual que un péndulo intercambia energía cinética y potencial.

En un circuito de tanque perfecto (sin resistencia), esta oscilación continuaría para siempre, al igual que un péndulo sin fricción continuaría oscilando a su frecuencia de resonancia para siempre. Pero las máquinas sin fricción son difíciles de encontrar en el mundo real, al igual que los circuitos de tanques sin pérdidas.

La energía perdida a través de la resistencia (o pérdidas del núcleo del inductor u ondas electromagnéticas radiadas o ...) en un circuito de tanque hará que las oscilaciones disminuyan en amplitud hasta que desaparezcan. Si hay suficientes pérdidas de energía en el circuito de un tanque, no resonará en absoluto.

El efecto amortiguador de Antiresonance es más que una simple curiosidad:se puede utilizar con bastante eficacia para eliminar no deseados oscilaciones en circuitos que contienen inductancias parásitas y / o capacitancias, como ocurre con casi todos los circuitos. Tome nota del siguiente circuito de retardo de tiempo L / R:(Figura siguiente)

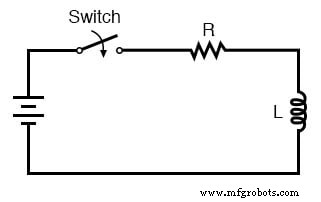
Circuito de retardo de tiempo L / R

La idea de este circuito es simple:“cargar” el inductor cuando el interruptor está cerrado. La tasa de carga del inductor se establecerá mediante la relación L / R, que es la constante de tiempo del circuito en segundos.

Sin embargo, si construyera un circuito de este tipo, es posible que encuentre oscilaciones inesperadas (CA) de voltaje en el inductor cuando el interruptor está cerrado. (Figura siguiente) ¿Por qué es esto? No hay condensador en el circuito, entonces, ¿cómo podemos tener una oscilación resonante con solo un inductor, una resistencia y una batería?

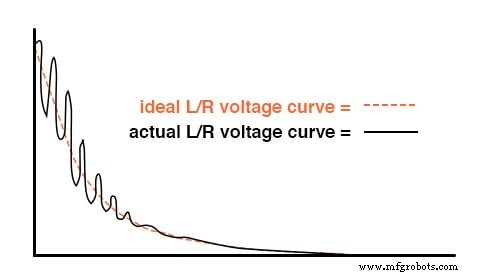
Inductor sonando debido a resonancia con capacitancia parásita.

Todos los inductores contienen una cierta cantidad de capacitancia parásita debido a los huecos de aislamiento entre vueltas y vueltas a núcleo. Además, la ubicación de los conductores del circuito puede crear una capacitancia parásita. Si bien el diseño limpio del circuito es importante para eliminar gran parte de esta capacitancia parásita, siempre habrá algunas que no se pueden eliminar.

Si esto causa problemas de resonancia (oscilaciones de CA no deseadas), la resistencia adicional puede ser una forma de combatirlo. Si la resistencia R es lo suficientemente grande, provocará una condición de antirresonancia, disipando suficiente energía para impedir que la inductancia y la capacitancia parásita sostengan oscilaciones durante mucho tiempo.

Curiosamente, el principio de emplear resistencia para eliminar la resonancia no deseada se utiliza con frecuencia en el diseño de sistemas mecánicos, donde cualquier objeto en movimiento con masa es un resonador potencial.

Una aplicación muy común de esto es el uso de amortiguadores en automóviles. Sin amortiguadores, los autos rebotarían violentamente a su frecuencia de resonancia después de golpear cualquier bache en la carretera. El trabajo del amortiguador es introducir un fuerte efecto antirresonante al disipar la energía hidráulicamente (de la misma manera que una resistencia disipa la energía eléctricamente).

REVISAR:

• La resistencia agregada a un circuito LC puede causar una condición conocida como antirresonancia , donde los efectos de la impedancia máxima ocurren en frecuencias distintas a las que dan reactancias capacitivas e inductivas iguales.
• La resistencia inherente a los inductores del mundo real puede contribuir en gran medida a las condiciones de antirresonancia. Una fuente de tal resistencia es el efecto piel , causado por la exclusión de la corriente alterna del centro de los conductores. Otra fuente es la de pérdidas de núcleo en inductores de núcleo de hierro.
• En un circuito LC en serie simple que contiene resistencia (un circuito "RLC"), la resistencia no producir antirresonancia. La resonancia todavía ocurre cuando las reactancias capacitivas e inductivas son iguales.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de resonancia