Factor Q y ancho de banda de un circuito resonante
El factor Q, o calidad, de un circuito resonante es una medida de la "bondad" o calidad de un circuito resonante. Un valor más alto para esta figura de mérito corresponde a un ancho de banda más estrecho, lo que es deseable en muchas aplicaciones. Más formalmente, Q es la relación entre la potencia almacenada y la potencia disipada en la reactancia y resistencia del circuito, respectivamente:
Q =P almacenado / P disipado =I 2 X / I 2 R Q =X / R donde:X =Reactancia capacitiva o inductiva en resonancia R =Resistencia en serie.
Esta fórmula es aplicable a circuitos resonantes en serie y también a circuitos resonantes en paralelo si la resistencia está en serie con el inductor. Este es el caso en aplicaciones prácticas, ya que nos preocupa principalmente la resistencia del inductor que limita el Q.
Nota: Algún texto puede mostrar X y R intercambiados en la fórmula "Q" para un circuito resonante paralelo. Esto es correcto para un valor grande de R en paralelo con C y L. Nuestra fórmula es correcta para un R pequeño en serie con L.
Una aplicación práctica de “Q” es que el voltaje a través de L o C en un circuito resonante en serie es Q veces el voltaje aplicado total. En un circuito resonante paralelo, la corriente a través de L o C es Q veces la corriente total aplicada.
Circuitos resonantes en serie
Un circuito resonante en serie parece una resistencia a la frecuencia resonante. Dado que la definición de resonancia es X L =X C , los componentes reactivos se cancelan, dejando solo la resistencia para contribuir a la impedancia.
La impedancia también es mínima en resonancia. Por debajo de la frecuencia resonante, el circuito resonante en serie parece capacitivo ya que la impedancia del capacitor aumenta a un valor mayor que la reactancia inductiva decreciente, dejando un valor capacitivo neto.
Por encima de la resonancia, la reactancia inductiva aumenta, la reactancia capacitiva disminuye, dejando un componente inductivo neto.
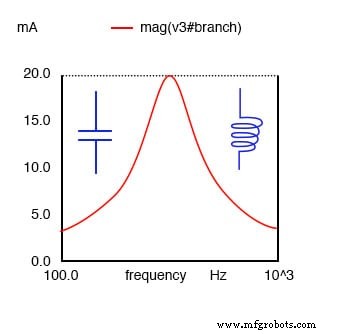
NOTA:
En resonancia, el circuito resonante en serie parece puramente resistivo. Por debajo de la resonancia parece capacitivo. Por encima de la resonancia, parece inductivo. La corriente es máxima en resonancia, impedancia mínima. La corriente se establece por el valor de la resistencia. Por encima o por debajo de la resonancia, la impedancia aumenta.
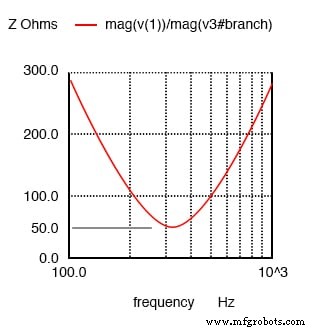
La impedancia es mínima en la resonancia en un circuito resonante en serie.
El pico de corriente resonante se puede cambiar variando la resistencia en serie, lo que cambia el Q. Esto también afecta la amplitud de la curva. Un circuito de baja resistencia y alta Q tiene un ancho de banda estrecho, en comparación con un circuito de alta resistencia y baja Q.
Ancho de banda en términos de Q y frecuencia de resonancia:
BW =f c / Q Donde f c =frecuencia de resonancia Q =factor de calidad
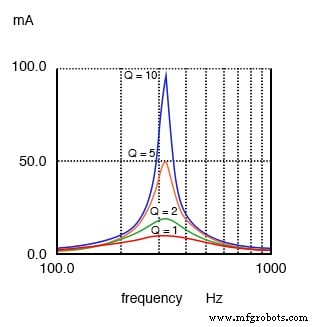
Un circuito resonante de Q alto tiene un ancho de banda estrecho en comparación con un Q bajo
El ancho de banda se mide entre los 0,707 puntos de amplitud de corriente. Los 0,707 puntos de corriente corresponden a la mitad de los puntos de potencia ya que P =I 2 R, (0,707) 2 =(0.5).
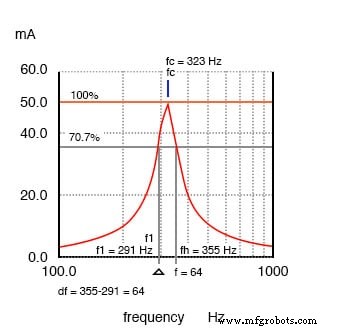
Ancho de banda, Δf se mide entre los puntos de amplitud del 70,7% del circuito resonante en serie.
BW =Δf =f h -f l =f c / Q Donde:f h =borde de banda alto f l =borde de banda baja f l =f c - Δf / 2 f h =f c + Δf / 2 donde f c =frecuencia central (frecuencia resonante)
En la Figura anterior, el punto de corriente del 100% es 50 mA. El nivel del 70,7% es .707 (50 mA) =35,4 mA. Los bordes de banda superior e inferior leídos en la curva son 291 Hz para fl y 355 Hz para f h . El ancho de banda es de 64 Hz y los puntos de media potencia son ± 32 Hz de la frecuencia resonante central:
BW =Δf =f h -f l =355-291 =64 f l =f c - Δf / 2 =323-32 =291 f h =f c + Δf / 2 =323 + 32 =355
Desde BW =fc / Q:
Q =f c / BW =(323 Hz) / (64 Hz) =5
Circuitos resonantes en paralelo
La impedancia de un circuito resonante paralelo es máxima en la frecuencia resonante. Por debajo de la frecuencia resonante, el circuito resonante paralelo parece inductivo ya que la impedancia del inductor es menor, lo que genera la mayor proporción de corriente.
Por encima de la resonancia, la reactancia capacitiva disminuye, atrayendo la corriente más grande, adquiriendo así una característica capacitiva.
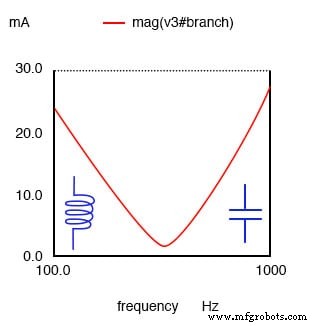
Un circuito resonante paralelo es resistivo en la resonancia, inductivo por debajo de la resonancia, capacitivo por encima de la resonancia.
La impedancia es máxima en resonancia en un circuito resonante paralelo, pero disminuye por encima o por debajo de la resonancia. El voltaje está en un pico en la resonancia ya que el voltaje es proporcional a la impedancia (E =IZ).
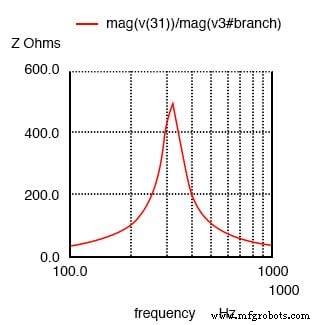
Circuito resonante paralelo:picos de impedancia en la resonancia.
Un Q bajo debido a una alta resistencia en serie con el inductor produce un pico bajo en una curva de respuesta amplia para un circuito resonante paralelo. Un Q alto se debe a una baja resistencia en serie con el inductor. Esto produce un pico más alto en la curva de respuesta más estrecha. El alto Q se logra enrollando el inductor con un cable de mayor diámetro (calibre más pequeño) y menor resistencia.
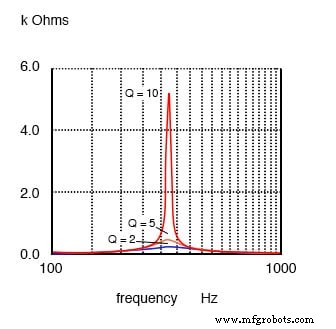
La respuesta de resonancia paralela varía con Q.
El ancho de banda de la curva de respuesta resonante paralela se mide entre los puntos de media potencia. Esto corresponde a los puntos de voltaje del 70,7% ya que la potencia es proporcional a E 2 . ((0,707) 2 =0.50) Dado que el voltaje es proporcional a la impedancia, podemos usar la curva de impedancia.
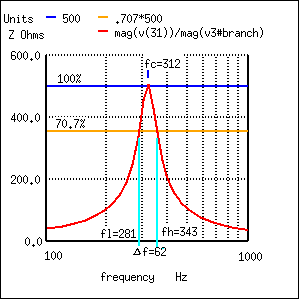
Ancho de banda, Δf se mide entre los puntos de impedancia del 70,7% de un circuito resonante paralelo.
En la figura anterior, el punto de impedancia del 100% es 500 Ω. El nivel del 70,7% es 0707 (500) =354 Ω. Los bordes de banda superior e inferior leídos en la curva son 281 Hz para fl y 343 Hz para fh. El ancho de banda es de 62 Hz y los puntos de media potencia son ± 31 Hz de la frecuencia resonante central:
BW =Δf =f h -f l =343-281 =62 f l =f c - Δf / 2 =312-31 =281 f h =f c + Δf / 2 =312 + 31 =343
Q =fc / BW =(312 Hz) / (62 Hz) =5
HOJAS DE TRABAJO RELACIONADAS:
- Hoja de trabajo de resonancia
- Hoja de trabajo de sustitución algebraica de circuitos eléctricos
Tecnología Industrial
- Leyes y ecuaciones del circuito de CC
- Puertas TTL NAND y AND
- Puertas TTL NOR y OR
- Voltaje y corriente en un circuito práctico
- ¿Qué son los circuitos en “serie” y “paralelo”?
- Series R, L y C
- Cálculo del factor de potencia
- Materiales y construcción del circuito flexible
- Factor Q en ingeniería eléctrica y electrónica
- Componentes de la placa de circuito y sus aplicaciones
- Retrocesos y soluciones en el diseño de PCB RF



