Series R, L y C

Tomemos el siguiente circuito de ejemplo y analicémoslo:

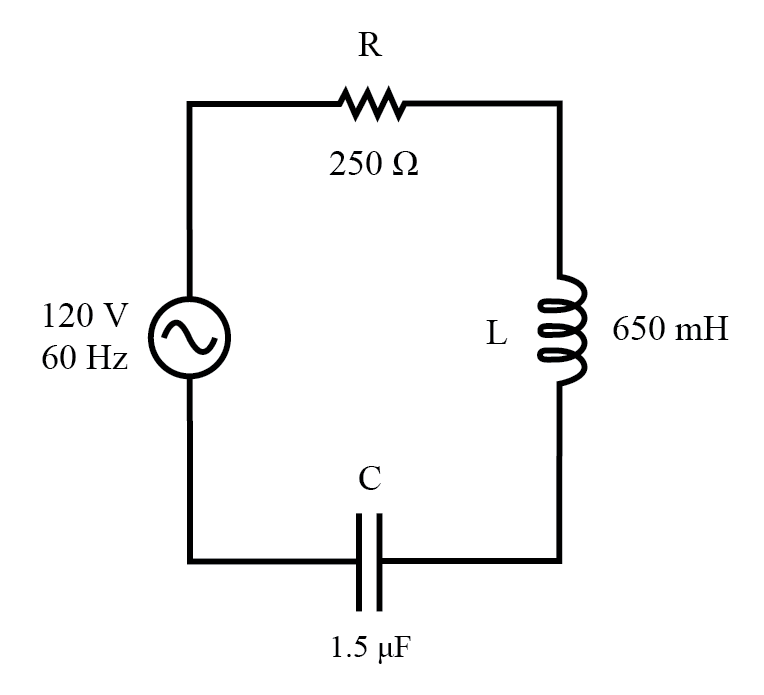
Circuito de serie R, L y C de ejemplo.

Resolución de reactancia

El primer paso es determinar la reactancia (en ohmios) del inductor y el condensador.

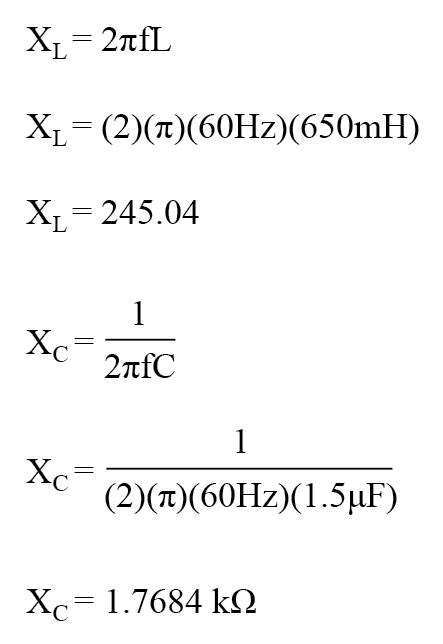
El siguiente paso es expresar todas las resistencias y reactancias en una forma matemáticamente común:impedancia. (Figura siguiente)

Recuerde que una reactancia inductiva se traduce en una impedancia imaginaria positiva (o una impedancia a + 90 °), mientras que una reactancia capacitiva se traduce en una impedancia imaginaria negativa (impedancia a -90 °). La resistencia, por supuesto, todavía se considera una impedancia puramente "real" (ángulo polar de 0 °):

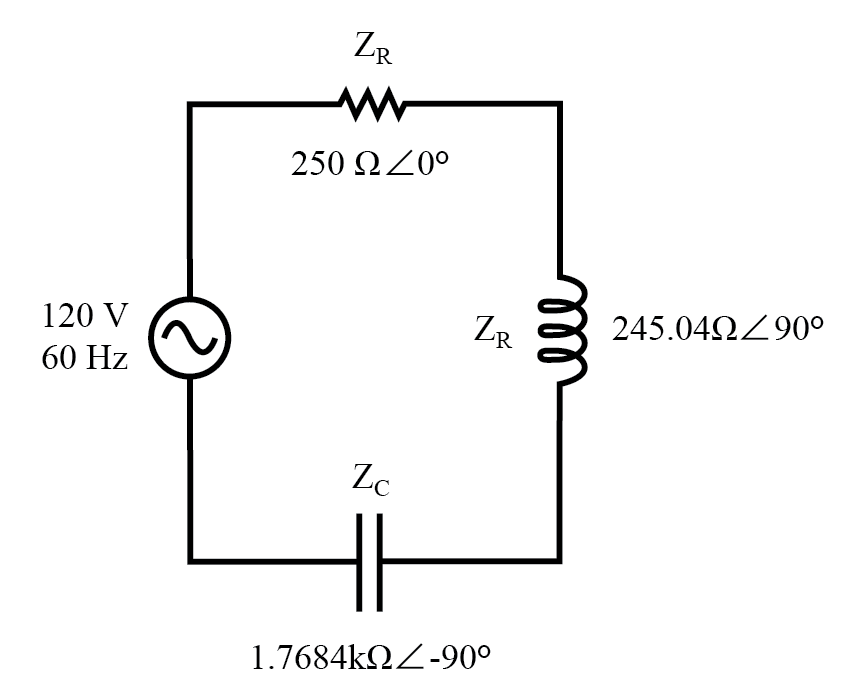
Circuito de serie R, L y C de ejemplo con valores de componentes reemplazados por impedancias.

Tabular resultados:

Ahora, con todas las cantidades de oposición a la corriente eléctrica expresadas en un formato de número complejo común (como impedancias, y no como resistencias o reactancias), se pueden manejar de la misma manera que las resistencias simples en un circuito de CC.

Este es un momento ideal para elaborar una tabla de análisis para este circuito e insertar todas las cifras "dadas" (voltaje total e impedancia del resistor, inductor y capacitor).

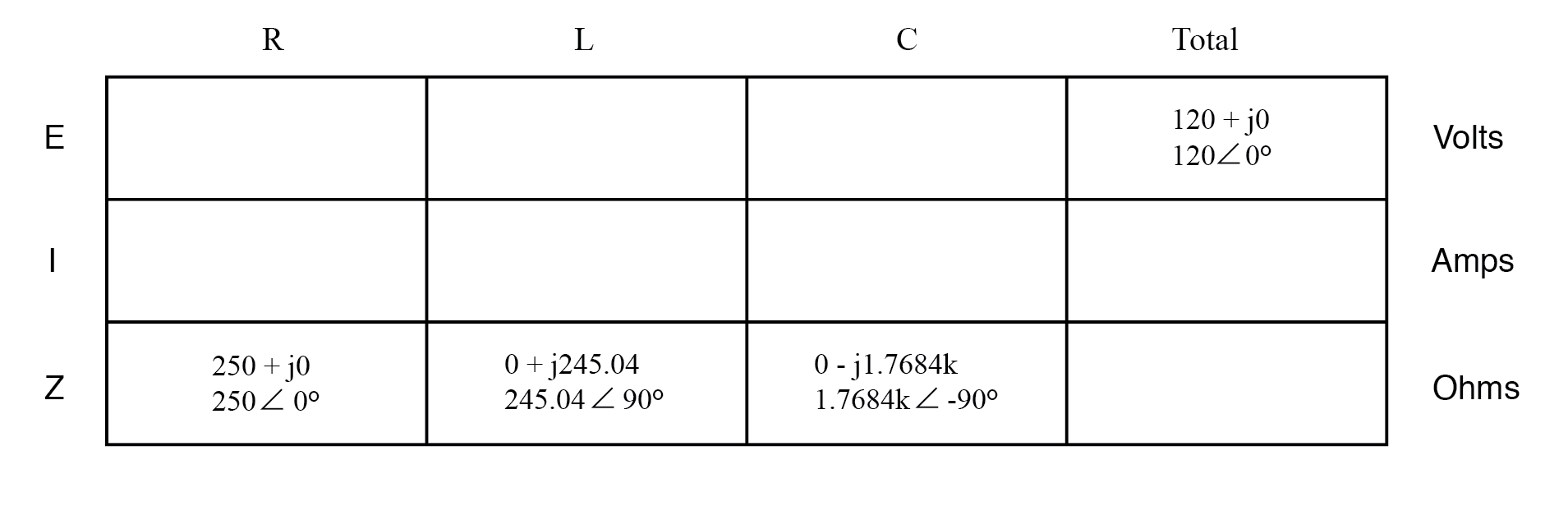
A menos que se especifique lo contrario, el voltaje de la fuente será nuestra referencia para el cambio de fase y, por lo tanto, se escribirá en un ángulo de 0 °. Recuerde que no existe un ángulo "absoluto" de cambio de fase para un voltaje o corriente, ya que siempre es una cantidad relativa a otra forma de onda.

Sin embargo, los ángulos de fase para la impedancia (como los de la resistencia, el inductor y el condensador) se conocen de manera absoluta, porque las relaciones de fase entre el voltaje y la corriente en cada componente están absolutamente definidas.

Observe que estoy asumiendo un inductor y un condensador perfectamente reactivos, con ángulos de fase de impedancia de exactamente +90 y -90 °, respectivamente.

Aunque los componentes reales no serán perfectos en este sentido, deberían estar bastante cerca. Para simplificar, asumiré inductores y condensadores perfectamente reactivos de ahora en adelante en mis cálculos de ejemplo, excepto donde se indique lo contrario.

Dado que el circuito de ejemplo anterior es un circuito en serie, sabemos que la impedancia total del circuito es igual a la suma de los individuos, así que:

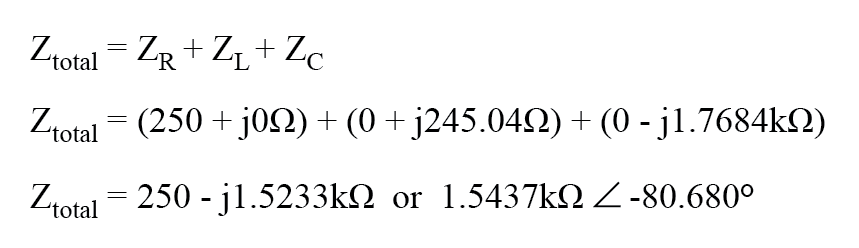
Insertando esta figura para la impedancia total en nuestra tabla:

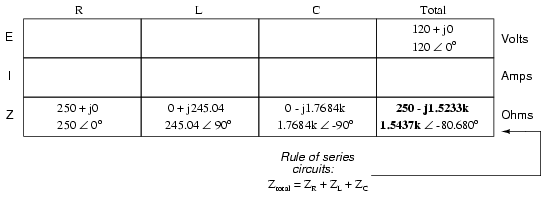
Ahora podemos aplicar la ley de Ohm (I =E / R) verticalmente en la columna "Total" para encontrar la corriente total para este circuito en serie:

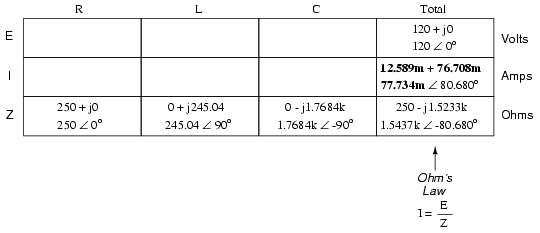
Al ser un circuito en serie, la corriente debe ser igual en todos los componentes. Así, podemos tomar la cifra obtenida para la corriente total y distribuirla a cada una de las otras columnas:

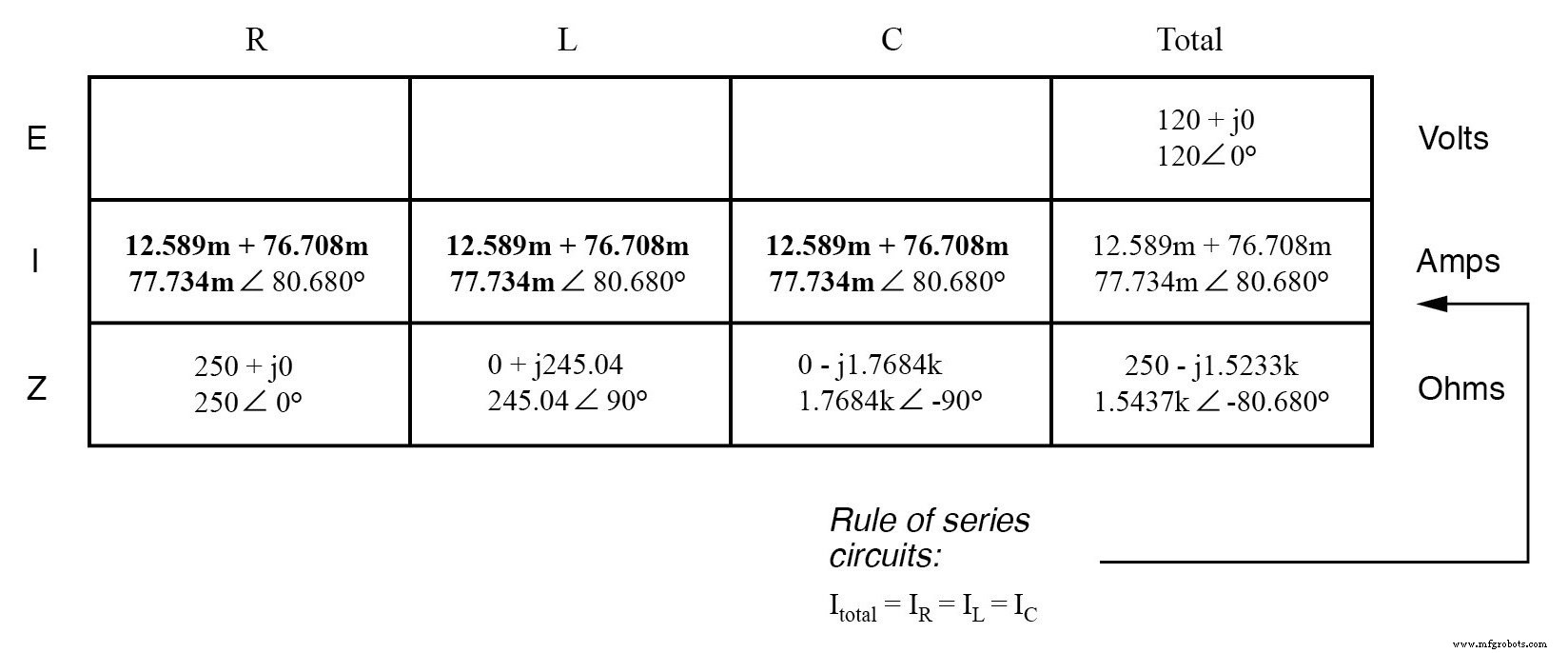
Ahora estamos preparados para aplicar la ley de Ohm (E =IZ) a cada una de las columnas de componentes individuales en la tabla, para determinar las caídas de voltaje:

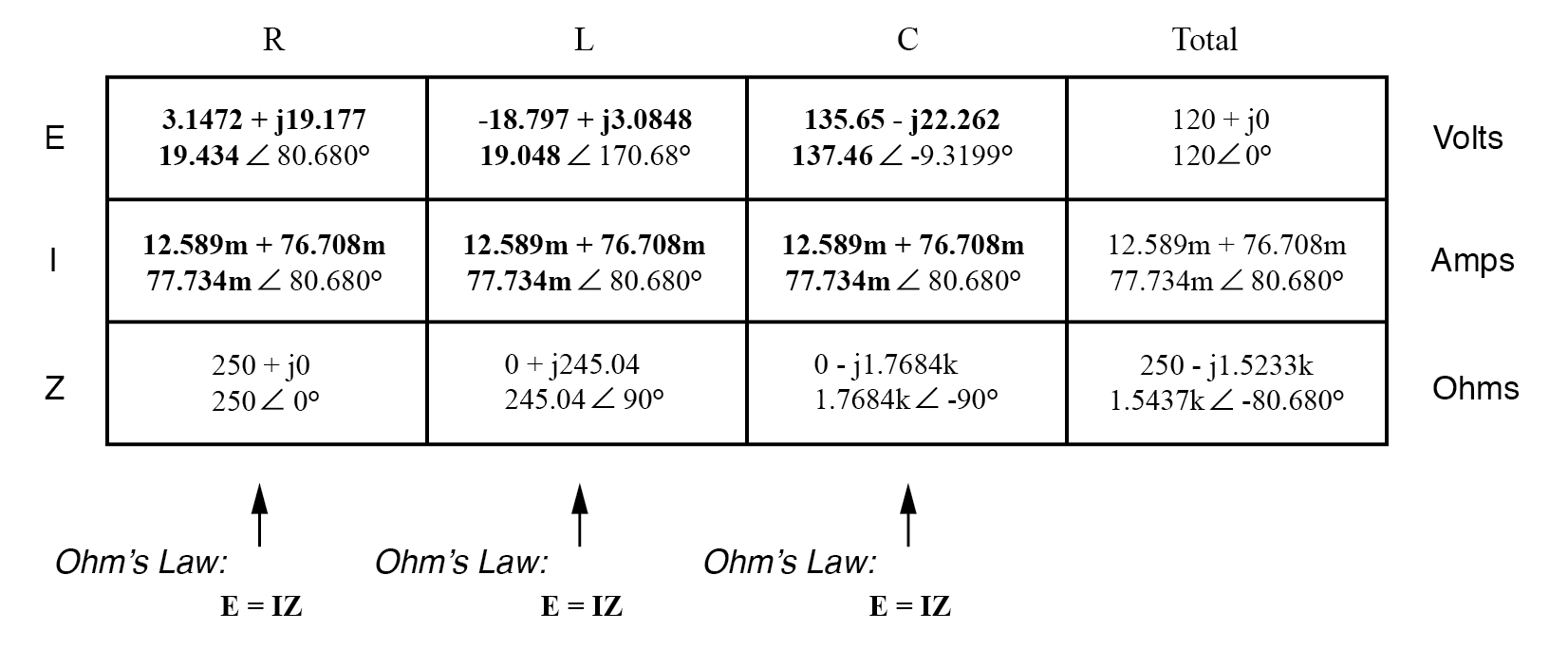
Observe algo extraño aquí:aunque nuestro voltaje de suministro es de solo 120 voltios, ¡el voltaje a través del capacitor es de 137,46 voltios! ¿Cómo puede ser esto? La respuesta está en la interacción entre las reactancias inductiva y capacitiva.

Expresadas como impedancias, podemos ver que el inductor se opone a la corriente de una manera exactamente opuesta a la del condensador. Expresada en forma rectangular, la impedancia del inductor tiene un término imaginario positivo y el capacitor tiene un término imaginario negativo.

Cuando estas dos impedancias contrarias se agregan (en serie), ¡tienden a anularse entre sí! Aunque todavía están agregados para producir una suma, esa suma es en realidad menos que cualquiera de las impedancias individuales (capacitivas o inductivas) por sí solas.

Es análogo a sumar un número positivo y uno negativo (escalar):la suma es una cantidad menor que el valor absoluto individual de cualquiera de los dos.

Si la impedancia total en un circuito en serie con elementos tanto inductivos como capacitivos es menor que la impedancia de cualquiera de los elementos por separado, entonces la corriente total en ese circuito debe ser mayor de lo que sería con solo los elementos inductivos o capacitivos allí.

Con esta corriente anormalmente alta a través de cada uno de los componentes, se pueden obtener voltajes mayores que el voltaje de la fuente en algunos de los componentes individuales. En el próximo capítulo se explorarán más consecuencias de las reactancias opuestas de los inductores y condensadores en el mismo circuito.

Una vez que haya dominado la técnica de reducir todos los valores de los componentes a impedancias (Z), analizar cualquier circuito de CA es tan difícil como analizar cualquier circuito de CC, excepto que las cantidades tratadas son vectoriales en lugar de escalares.

Con la excepción de las ecuaciones que tratan con la potencia (P), las ecuaciones en los circuitos de CA son las mismas que las de los circuitos de CC, utilizando impedancias (Z) en lugar de resistencias (R). La ley de Ohm (E =IZ) sigue siendo válida, al igual que las leyes de voltaje y corriente de Kirchhoff.

Para demostrar la ley de voltaje de Kirchhoff en un circuito de CA, podemos observar las respuestas que obtuvimos para las caídas de voltaje de los componentes en el último circuito. KVL nos dice que la suma algebraica de las caídas de voltaje a través de la resistencia, el inductor y el capacitor debe ser igual al voltaje aplicado desde la fuente.

Aunque esto no parezca cierto a primera vista, un poco de suma de números complejos demuestra lo contrario:

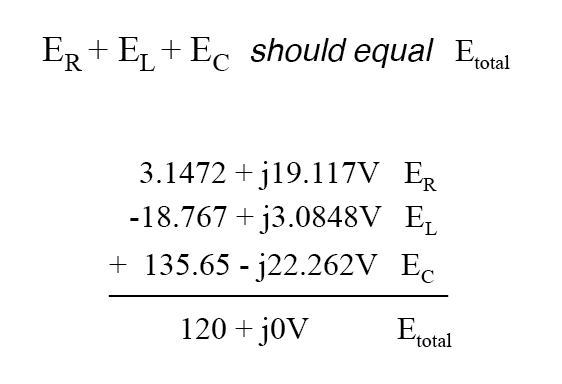
Aparte de un pequeño error de redondeo, la suma de estas caídas de voltaje es igual a 120 voltios. Realizado en una calculadora (conservando todos los dígitos), la respuesta que recibirá debe ser exactamente 120 + j0 voltios.

También podemos usar SPICE para verificar nuestras cifras para este circuito:

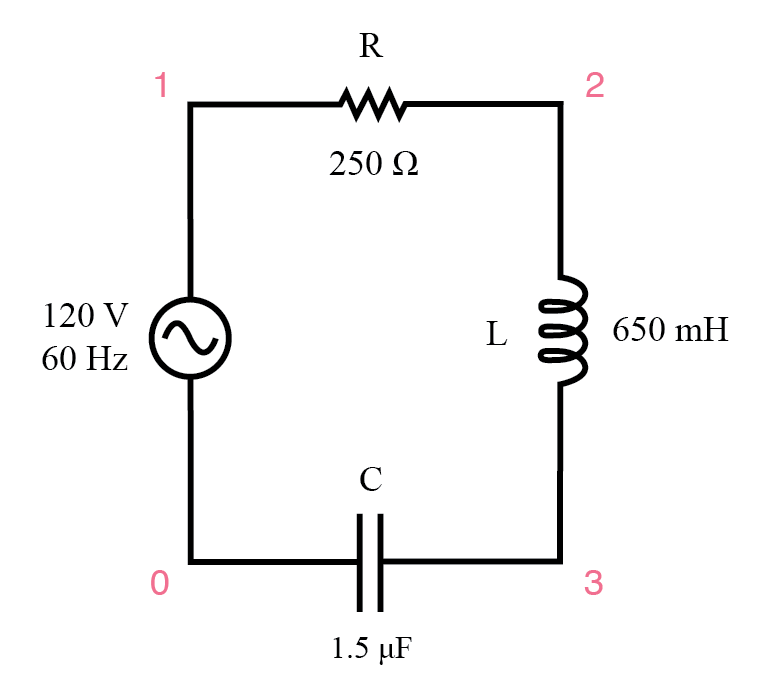
Ejemplo de circuito SPICE de las series R, L y C.

 r1 1 2 250 l1 2 3 650m c1 3 0 1.5u .ac lin 1 60 60 .imprimir ac v (1,2) v (2,3) v (3,0) i (v1) .print ac vp (1,2) vp (2,3) vp (3,0) ip (v1) .fin frecuencia v (1, 2) v (2, 3) v (3) yo (v1) 6.000E + 01 1.943E + 01 1.905E + 01 1.375E + 02 7.773E-02 frecuencia vp (1,2) vp (2,3) vp (3) ip (v1) 6.000E + 01 8.068E + 01 1.707E + 02 -9.320E + 00 -9.932E + 01 

La simulación SPICE muestra que nuestros resultados calculados a mano son precisos.

Como puede ver, hay poca diferencia entre el análisis de circuitos de CA y el análisis de circuitos de CC, excepto que todas las cantidades de voltaje, corriente y resistencia (en realidad, impedancia ) debe manejarse en forma compleja en lugar de escalar para tener en cuenta el ángulo de fase.

Esto es bueno porque significa que todo lo que ha aprendido sobre los circuitos eléctricos de CC se aplica a lo que está aprendiendo aquí. La única excepción a esta coherencia es el cálculo del poder, que es tan único que merece un capítulo dedicado exclusivamente a ese tema.

REVISAR:

• Impedancias de cualquier tipo agregan en serie:Z _Total =Z ₁ + Z ₂ +. . . Z _n
• Aunque las impedancias se suman en serie, la impedancia total para un circuito que contiene tanto inductancia como capacitancia puede ser menor que una o más de las impedancias individuales, porque las impedancias inductivas y capacitivas en serie tienden a anularse entre sí. ¡Esto puede provocar caídas de voltaje en los componentes que excedan el voltaje de suministro!
• Todas las reglas y leyes de los circuitos de CC se aplican a los circuitos de CA, siempre que los valores se expresen en forma compleja en lugar de escalar. La única excepción a este principio es el cálculo de potencia , que es muy diferente para AC.

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de circuitos de CA combinados en serie-paralelo