Conmutación de giro controlable en una unión de túnel magnético de una sola molécula
Resumen
Se propone un nuevo tipo de filtro de corriente de espín que consiste en un imán de molécula única (SMM) acoplado a dos electrodos metálicos normales. Se muestra que esta unión de túnel puede generar una corriente altamente polarizada de espín, cuya polarización de espín puede conmutarse mediante campos magnéticos y voltajes de compuerta aplicados al SMM. Esta conmutación de espín en la unión del túnel SMM surge de la tunelización resonante de un solo electrón selectivo de espín a través de la órbita molecular desocupada más baja del SMM. El espectro de la corriente de electrones todavía está polarizado en el espín en ausencia de un campo magnético externo, lo que puede ayudar a juzgar si el estado de espín de la molécula ha alcanzado el doblete del estado fundamental \ (| \ pm S \ rangle \). Este dispositivo se puede realizar con las tecnologías actuales y puede tener un uso práctico en la espintrónica y la información cuántica.
Introducción
Con el desarrollo de la ciencia de los materiales, los dispositivos electrónicos moleculares a nanoescala se han estudiado ampliamente en los últimos años con respecto a sus aplicaciones potenciales en dispositivos a nanoescala y espintrónica [1, 2, 3]. Debido a su pequeño tamaño y bajo consumo de energía, se han demostrado muchos dispositivos básicos que utilizan moléculas, incluyendo uniones de túnel con resistencia diferencial negativa [4], rectificadores [5], amplificadores [6] y almacenamiento de datos [7]. A diferencia de los dispositivos semiconductores convencionales, los dispositivos moleculares que constan de moléculas individuales parecen ser bastante adecuados para funcionar como interruptores moleculares controlables [8]. Aunque se ha informado de cambios de escala molecular en contactos de puntos cuánticos atómicos [9,10,11], las uniones de una sola molécula proporcionan la flexibilidad adicional de la capacidad de ajustar los estados de conductancia on / off a través del diseño molecular. Después de la medición exitosa de los flujos de corriente a través de moléculas individuales en las últimas décadas, se han reportado varios tipos de interruptores moleculares, como interruptores moleculares controlados por luz [12] e interruptores de una sola molécula controlados mecánicamente [13], que se pueden utilizar para cambiar un dispositivo entre estados de alta y baja conductancia. Sin embargo, todos estos esquemas de conmutación solo permiten el ajuste de la conductancia de transporte de carga, no las características de transporte dependientes del giro.
En los últimos años, se ha demostrado que un nuevo tipo de material molecular conocido como imán de molécula única (SMM) es un candidato apropiado como componente básico de los dispositivos espintrónicos basados en moléculas [14]. A diferencia de otras moléculas, un SMM es una molécula con un momento de giro neto relativamente grande (correspondiente al número de giro S ) y anisotropía magnética uniaxial significativa [15]. A bajas temperaturas, un SMM quedará atrapado en uno de los dos estados de giro metaestables \ (| \ pm S \ rangle \) [16]. Esta biestabilidad hace que los SMM sean una base adecuada para las células de memoria [17, 18] y ha motivado muchos esfuerzos para investigar las otras propiedades físicas de los SMM. Hasta ahora, las transiciones de electrones entre un SMM y un metal normal [19,20,21] o interfaces superconductores [22] se han investigado experimentalmente, y las funcionalidades de escribir y leer información hacia y desde un SMM por medio de campos magnéticos y eléctricos. También se han demostrado sesgos en la molécula \ (\ hbox {TbPc} _ {{2}} \) [23]. Inspirándose en estos trabajos, se espera que la polarización de espín de la corriente de túnel en un SMM también pueda conmutarse mediante campos magnéticos y voltajes de compuerta; sin embargo, todavía no se han propuesto esquemas de conmutación controlables basados en una unión de túnel SMM.
Métodos
En esta carta, presentamos un nuevo tipo de efecto de cambio de espín en una unión de túnel SMM que se puede usar para cambiar entre corrientes electrónicas de espín hacia arriba y hacia abajo puras cambiando los campos magnéticos externos aplicados a la molécula. Como se muestra en la Fig. 1a, esta nanoestructura consiste en un SMM conectado a dos electrodos metálicos normales. El nivel de energía del SMM está sintonizado por el voltaje de la puerta, y la magnetización de espín del SMM se puede cambiar mediante un campo magnético externo. En la Fig. 1b, podemos ver que la inyección de espín controlada por campo magnético en este dispositivo necesita un esquema de dos pasos:Primero, aplica un campo magnético externo relativamente más grande para "escribir" una orientación de espín del SMM. El giro del núcleo del SMM se cambiará a uno de los dos estados de giro metaestables \ (\ pm \, S \), dependiendo de la dirección del campo magnético. Y el proceso de inyección de espín consiste en utilizar una polarización eléctrica ejercida a través de los dos cables en ausencia de un campo magnético. Debido al potencial químico diferente de los dos cables y la anisotropía magnética del SMM, solo los electrones con el espín paralelo a la magnetización del SMM pueden fluir a través de la unión [14], lo que hace que la corriente esté altamente polarizada. El hamiltoniano total del sistema se escribe como [24, 25]
$$ \ begin {alineado} H &=\ varepsilon _ {0} \ sum _ {\ sigma} c _ {\ sigma} ^ {\ dag} c _ {\ sigma} + Uc _ {\ uparrow} ^ {\ dag} c_ { \ uparrow} c _ {\ downarrow} ^ {\ dag} c _ {\ downarrow} - {\ mathcal {D}} (S ^ {z}) ^ {2} -J {\ mathbf {s}} \ cdot {\ mathbf {S}} \ nonumber \\ &\ quad - \ Delta B (s ^ {z} + S ^ {z}) + \ sum _ {k, \ sigma, \ alpha} (t _ {\ alpha} a_ { \ alpha k \ sigma} ^ {\ dag} c _ {\ sigma} + t ^ {*} _ {\ alpha} c ^ {\ dag} _ {\ sigma} a _ {\ alpha k \ sigma}) \ nonumber \ \ &\ quad + \ sum _ {k, \ sigma, \ alpha} \ varepsilon _ {k \ sigma} a _ {\ alpha k \ sigma} ^ {\ dag} a _ {\ alpha k \ sigma}. \ end {alineado} $$ (1)Aquí, \ (\ varepsilon _ {0} \) es la energía en el sitio del orbital molecular desocupado más bajo (LUMO) del SMM, que se puede cambiar mediante un voltaje de puerta aplicado al SMM; \ (c _ {\ sigma} ^ {\ dag} \) (\ (c _ {\ sigma} \)) es el operador de creación (aniquilación) de electrones con \ (\ sigma \) como índice de giro de Pauli; U denota la energía de repulsión de Coulomb; y \ ({\ mathcal {D}} \) es el parámetro de anisotropía uniaxial magnética. J es la interacción de intercambio entre el espín de los electrones conductores, \ ({\ mathbf {s}} =\ sum \ nolimits _ {\ sigma \ sigma ^ {\ prime}} c _ {\ sigma} ^ {\ dag} \ sigma _ {\ sigma \ sigma ^ {\ prime}} c _ {\ sigma ^ {\ prime}} / 2 \), en el nivel LUMO y el giro local \ ({\ mathbf {S}} \). Dado que asumimos que el eje fácil de la molécula es el eje z en el espacio de espín, \ (\ Delta B (s ^ {z} + S ^ {z}) \) describe la división de Zeeman asociada con el campo magnético aplicado a lo largo de este sencillo eje, donde el g factor y el magnetón de Bohr \ (\ mu _ {B} \) se absorben en \ (\ Delta B \). \ (a _ {\ alpha k \ sigma} ^ {\ dag} \) (\ (a _ {\ alpha k \ sigma} \)) es el operador de creación (aniquilación) para electrones con impulso k , giro \ (\ sigma \) y energía \ (\ varepsilon _ {k \ sigma} \) en el plomo \ (\ alpha \). La fuerza de acoplamiento de túnel entre el SMM y los cables metálicos normales, que se denota por \ (t _ {\ alpha} \), es independiente del impulso k y gire \ (\ sigma \).
Es fácil diagonalizar el hamiltoniano \ (H _ {{\ mathrm {mol}}} \) del SMM aislado, es decir, los primeros cinco términos en la ecuación. (1). Si definimos \ ({\ mathbf {S}} _ {T} ={\ mathbf {s}} + {\ mathbf {S}} \), se puede demostrar que el valor propio m de \ (S_ {T} ^ {z} \) es un buen número cuántico debido a la relación de conmutación \ ([S_ {T} ^ {z}, H _ {{\ mathrm {mol}}}] =0 \) . En las siguientes expresiones, \ (| \ bullet \ rangle _ {L ({\ mathrm {mol}})} \) representa el estado de giro de LUMO (SMM). Con \ (n =0,1,2 \) definido como el número de electrones en el LUMO, las energías propias se pueden obtener de la siguiente manera [26]:\ (\ varepsilon _ {| 0, m \ rangle} =- {\ mathcal {D}} m ^ {2} - \ Delta Bm \) para los estados propios \ (| 0, m \ rangle =| 0 \ rangle _ {L} \ otimes | m \ rangle _ {{\ mathrm {mol} }} \), \ (\ varepsilon _ {| 1, m \ rangle ^ {\ pm}} =\ varepsilon _0 - \ Delta B m + J / 4 - {\ mathcal {D}} (m ^ {2} +1/4) \ pm \ Delta \ varepsilon (m) \) para los estados propios \ (| 1, m \ rangle ^ {\ pm} =C_ {1} ^ {\ pm} | \ flecha abajo \ rangle _ {L } \ otimes | m + 1/2 \ rangle _ {{\ mathrm {mol}}} + C_ {2} ^ {\ pm} | \ uparrow \ rangle _ {L} \ otimes | m-1/2 \ rangle _ {{\ mathrm {mol}}} \) y \ (\ varepsilon _ {| 2, m \ rangle} =2 \ varepsilon _0 + U - {\ mathcal {D}} m ^ {2} - \ Delta B m \) para los estados propios \ (| 2, m \ rangle =| \ uparrow \ downarrow \ rangle _ {L} \ otimes | m \ rangle _ {{\ mathrm {mol}}} \). Aquí, \ (\ Delta \ varepsilon (m) =\ sqrt {{\ mathcal {D}} ({\ mathcal {D}} - J) m ^ {2} + (J / 4) ^ {2} (2S +1) ^ {2}} \), y \ (C_ {1} ^ {\ pm} \) y \ (C_ {2} ^ {\ pm} \), que se dan en la Ref. [24], actúan como coeficientes de Clebsch-Gordan efectivos.
El proceso de transporte está dominado por la tunelización secuencial a través del nivel SMM, mientras que la tunelización débil y la tunelización directa pueden descuidarse de forma segura. Para el acoplamiento débil entre el SMM y los cables, se mantiene el enfoque de la ecuación maestra. La corriente de giro total - \ (\ sigma \) que fluye a través del SMM se puede escribir como \ (I _ {\ sigma} =(I_ {L \ sigma} -I_ {R \ sigma}) / 2 \), donde \ ( I_ {L \ sigma} \) (\ (I_ {R \ sigma} \)) representa el giro - \ (\ sigma \) corriente que fluye desde el cable izquierdo (derecho) al SMM, produciendo
$$ \ begin {alineado} I _ {\ alpha \ sigma} =- (e / h) \ sum _ {i, f} (n_ {i} -n_ {f}) R _ {\ alpha \ sigma} ^ {f \ rightarrow i} P_ {f}, \ end {alineado} $$ (2)tal que la corriente total es igual a \ (I =\ sum _ {\ sigma} (I_ {L \ sigma} -I_ {R \ sigma}) / 2 \) y el coeficiente de polarización de espín de la corriente es \ (\ eta =\ frac {I _ {\ alpha \ uparrow} - I _ {\ alpha \ downarrow}} {I _ {\ alpha}} \ times 100 \% \). En Eq. (2), \ (R _ {\ alpha \ sigma} ^ {f \ rightarrow i} \) denota la tasa de transición entre los estados \ (| i \ rangle \) y \ (| f \ rangle \), expresada como \ ( R _ {\ alpha \ sigma} ^ {f \ rightarrow i} =\ Gamma _ {\ alpha \ sigma} [f (\ varepsilon _ {i} - \ varepsilon _ {f} - \ mu _ {\ alpha}) \ langle i | c _ {\ sigma} ^ {\ dag} | f \ rangle ^ {2} + f (\ varepsilon _ {i} - \ varepsilon _ {f} + \ mu _ {\ alpha}) \ langle f | c _ {\ sigma} ^ {\ dag} | i \ rangle ^ {2}] \), donde \ (\ Gamma _ {\ alpha \ sigma} =2 \ pi D _ {\ alpha \ sigma} | t _ {\ alpha } | ^ {2} \) es la función de ancho de línea para la derivación \ (\ alpha \), siendo \ (D _ {\ alpha \ sigma} \) la densidad de estados en \ (E_ {F} \), y \ (f _ {\ alpha} \) es la función de Fermi del plomo \ (\ alpha \) a temperatura \ (T _ {\ alpha} \) y potencial químico \ (\ mu _ {\ alpha} \). \ (P_ {i} \) denota la probabilidad de encontrar el SMM en el estado \ (| i \ rangle \). Siguiendo el método numérico sugerido por Timm [26] y Shen [27], la dependencia temporal de la probabilidad \ (P_ {i (t)} \) y la probabilidad de estado estable \ (P_ {i (t \ rightarrow \ infty )} \) se puede obtener resolviendo un conjunto de ecuaciones de tasa \ ({\ mathrm {d}} P_ {i} / {\ mathrm {d}} t =\ sum _ {f} R_ {i, f} P_ {i} \).
Aquí, los cálculos numéricos se realizan para \ (\ hbox {Mn} _ {{12}} \) - Ac uniones de túnel molecular [19, 28], con número de giro \ (S =10 \), \ ({\ mathcal { D}} =0.06 \) meV, \ (J =0.1 \) meV y \ (U =25 \) meV. Los electrodos en consideración están hechos de metal normal, por lo que las funciones de ancho de línea son independientes del giro, es decir, \ (\ Gamma _ {\ alpha \ sigma} =\ Gamma _ {0} \) por simplicidad.
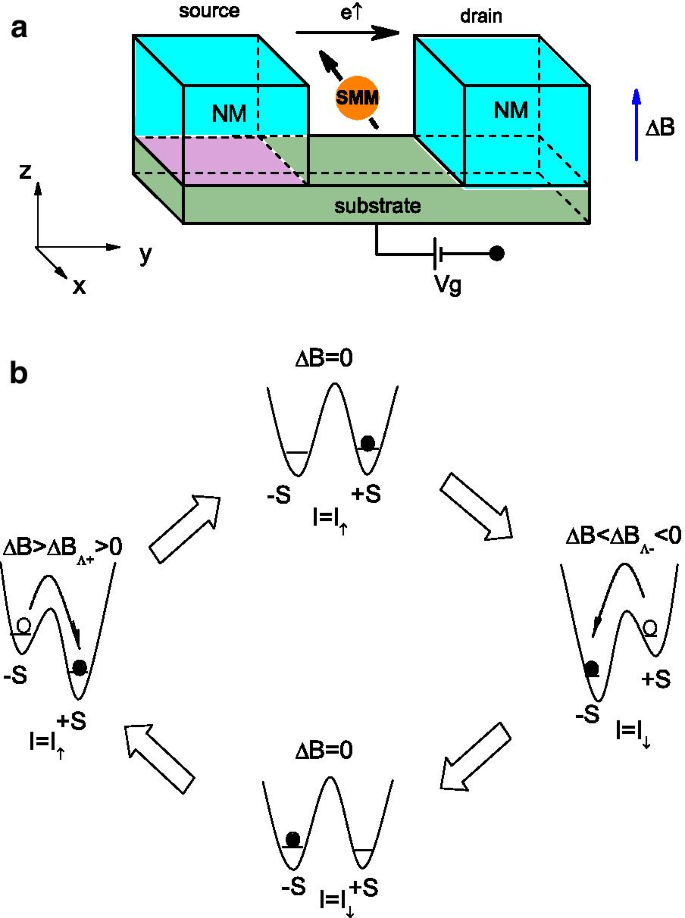
un Diagrama esquemático de un filtro de giro o memoria de giro que consta de un SMM acoplado a un par de electrodos no magnéticos. b Ilustración esquemática de la conmutación de la magnetización del SMM y la polarización de espín de la corriente de túnel por medio de campos magnéticos externos
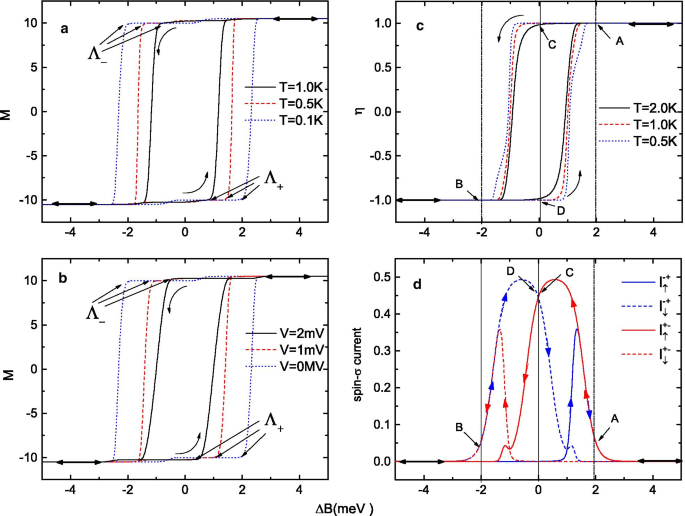
un , b Bucles de histéresis magnética del SMM para a diferentes temperaturas de equilibrio y b diferentes voltajes de polarización cuando el campo magnético externo \ (\ Delta B \) se escanea hacia adelante y hacia atrás. c Polarización de giro de la corriente de túnel para diferentes temperaturas de equilibrio y d spin - \ (\ sigma \) corrientes (escaladas por \ (e \ Gamma_ {0} / \ hbar \)) en \ (T =0.5 \) K cuando el campo magnético externo \ (\ Delta B \) se escanea hacia atrás y adelante bajo un sesgo fijo de \ (V =1 \) mV
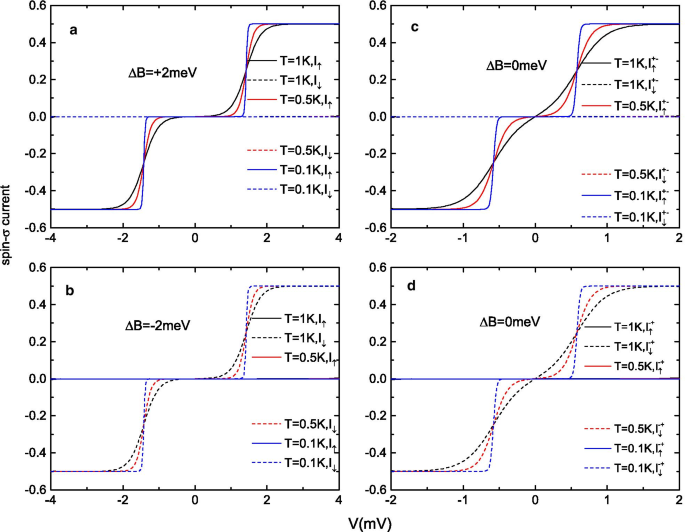
Giro - \ (\ sigma \) corrientes \ (I _ {\ uparrow (\ downarrow)} \) (escalado por \ (e \ Gamma_ {0} / \ hbar \)) ( a , b ) en presencia de campos magnéticos externos de a \ (\ Delta B =+ 2 \) meV, b \ (\ Delta B =- \, 2 \) meV, c , d en ausencia de un campo magnético en función de la tensión de polarización
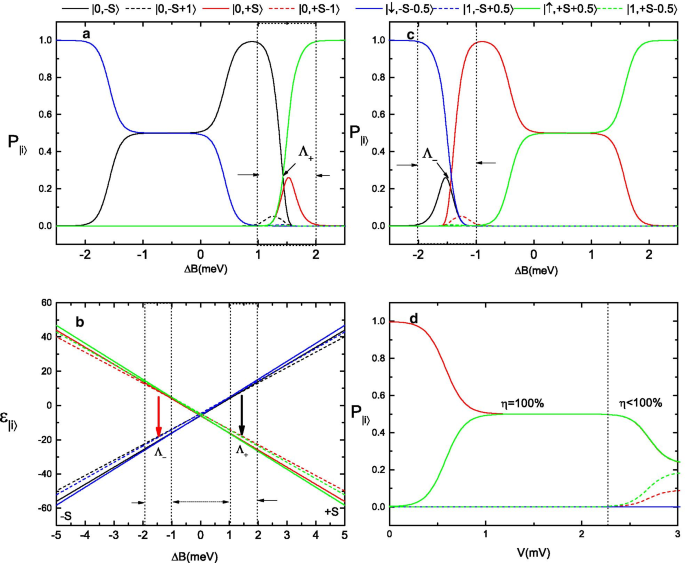
un , c Variaciones en las probabilidades del estado molecular a como \ (\ Delta B \) se escanea desde \ ({-} \, 5 \) meV a \ ({+} \, 5 \) meV y c ya que \ (\ Delta B \) se escanea desde \ (+ \, 5 \) meV a \ ({-} \, 5 \) meV. b Diagrama de Zeeman para estos estados de espín cuando \ (\ Delta B \) cambia de \ ({-} \) 5 meV a \ ({+} \) 5 meV. d Variaciones en las probabilidades del estado molecular como funciones del voltaje de polarización cuando el estado de giro de la molécula se prepara inicialmente de manera que \ (P_ {| 0, + S \ rangle} =1 \) y \ (P_ {i} =0 \)
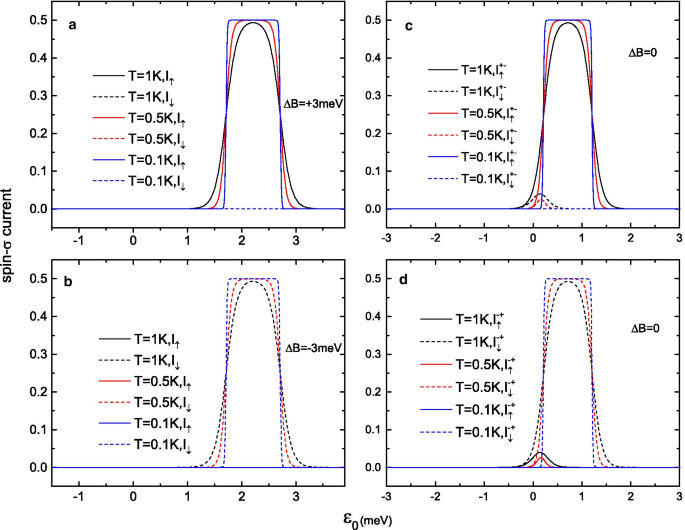
Girar - \ (\ sigma \) corrientes \ (I _ {\ uparrow (\ downarrow)} \) a , b en presencia de un campo magnético externo de un \ (B =+ 2 \) meV o b \ (B =- \, 2 \) meV y c , d en ausencia de un campo magnético en función del nivel molecular \ (\ varepsilon _ {0} \)
Resultados y discusión
Primero, demostramos cómo usar un campo magnético \ (\ Delta B \) para "escribir" los estados de giro de un SMM. En la Fig.2, graficamos la magnetización del SMM, la polarización de espín \ (\ eta \) de la corriente y las corrientes de espín - \ (\ sigma \) como funciones de \ (\ Delta B \), con un sesgo voltaje ejercido a través de la unión. Las flechas indican la dirección de exploración del campo magnético, y se supone que el proceso de exploración es lo suficientemente lento como para permitir que el sistema se relaje hasta un estado estable. En la Fig. 2a-c, se muestra que tanto la magnetización de la molécula como la polarización de espín de la corriente exhiben estructuras de bucle cuando el campo magnético \ (\ Delta B \) se explora hacia adelante y hacia atrás. Para facilitar la descripción, usamos \ (\ Lambda _ {-} \) para denotar el punto de inversión cuando la magnetización del SMM cambia de \ (+ S \ rightarrow -S \) y \ (\ Lambda _ {+} \ ) para denotar el punto de inversión de \ (- S \ rightarrow + S \). La magnetización del SMM se representa como una función de \ (\ Delta B \) para diferentes temperaturas de equilibrio y voltajes de polarización en la figura 2a, b. Es evidente que las fluctuaciones térmicas y el sesgo eléctrico pueden activar la inversión magnética antes de que \ (\ Delta B \) alcance exactamente la energía de activación. En consecuencia, el bucle de histéresis magnética se contrae a medida que aumenta la temperatura de equilibrio o el voltaje de polarización, y la distancia entre \ (\ Lambda _ {+} \) y \ (\ Lambda _ {-} \) disminuye. Sin embargo, no importa cuánto se contraiga el bucle de histéresis magnética, el coeficiente de polarización de espín de la corriente de túnel siempre puede alcanzar valores extremadamente altos de \ (\ eta =\ pm 100 \% \) excepto cuando \ (\ Delta B \) está cerca los dos puntos de inversión, \ (\ Lambda _ {+} \) y \ (\ Lambda _ {-} \). Además, se encuentra que la polarización de espín de la corriente en el régimen de campo magnético pequeño \ (\ Delta B _ {\ Lambda _ {-}} <\ Delta B <\ Delta B _ {\ Lambda _ {+}} \ ) es bastante diferente del régimen de campo magnético grande \ (\ Delta B <<\ Delta B _ {\ Lambda _ {-}} \) o \ (\ Delta B>> \ Delta B _ {\ Lambda _ { +}} \). Como se muestra en la Fig. 2c, en el régimen de campo magnético grande, el coeficiente de polarización de espín \ (\ eta \) de la corriente de efecto túnel se puede resumir como
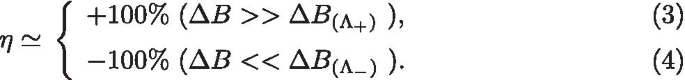
En este régimen, por ejemplo, en el punto A (punto B) de la figura 2c, d, un campo magnético externo dado \ (\ Delta B \) corresponde a una magnetización determinista única de la molécula, y solo a \ (100 \% \) la corriente de electrones spin-up (spin-down) puede fluir a través de la unión. Sin embargo, en el régimen de campo magnético bajo \ (\ Delta B _ {\ Lambda _ {-}} <\ Delta B <\ Delta B _ {\ Lambda _ {+}} \), la magnetización original del SMM puede permanecer sin cambios, y las direcciones de giro \ (+ S \) y \ (- S \) pueden conservarse. En la figura 2d, trazamos las curvas \ (I _ {\ sigma} \) - \ (\ Delta B \) para la unión SMM a una temperatura de equilibrio fija de \ (T =1 \) K y un voltaje de \ ( V =1 \) mV. Se muestra claramente que una sola \ (\ Delta B \) corresponde a dos posibles magnetizaciones de la molécula. Si usamos \ (I _ {\ sigma} ^ {+ -} \) para denotar el giro - \ (\ sigma \) actual cuando \ (\ Delta B \) se escanea desde \ (+ 5 \) meV a \ ( -5 \) meV y \ (I _ {\ sigma} ^ {- +} \) para indicar la corriente cuando el campo magnético se escanea en la dirección opuesta (\ (\ Delta B \) cambia de -5 meV a +5 meV), entonces ambas direcciones de giro del SMM en \ (+ S \) o \ (- S \) se pueden leer con diferentes características de polarización de giro en el régimen bajo - \ (\ Delta B \) (como en los puntos C y D en la Fig. 2c, d). En la figura 2c, el coeficiente de polarización de espín \ (\ eta \) de la corriente de túnel en el régimen de campo magnético pequeño \ (\ Delta B _ {\ Lambda _ {-}} <\ Delta B <\ Delta B _ {\ Lambda _ {+}} \) se puede resumir como
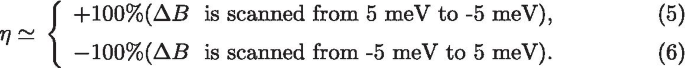
Más importante aún, como se muestra en la Fig. 2d, observamos que la intensidad de la corriente de túnel en \ (\ Delta B =0 \), es decir, en el punto C o D, es mucho mayor que en el régimen de campo magnético grande bajo el mismo voltaje de polarización de \ (V =1 \) mV. Esto significa que este dispositivo generará más fácilmente corrientes de electrones con polarización de espín en ausencia de un campo magnético externo, lo que lo hace adecuado como filtro de espín o dispositivo de memoria de espín.
Para discutir las capacidades de inyección de espín de esta unión molecular, graficamos las corrientes de espín - \ (\ sigma \) como funciones del voltaje de polarización a un voltaje de puerta constante y temperaturas más bajas. La Figura 3a, b muestra la \ (I _ {\ uparrow (\ downarrow)} \) - V curvas en valores de campo magnético grandes de \ (\ Delta B =\ pm 2 \) meV (correspondientes a los campos magnéticos en los puntos A y B en la Fig. 2), mientras que la Fig. 3c, d muestra las curvas en ausencia de \ (\ Delta B \) (correspondiente a los puntos C y D en la Fig. 2). Independientemente del régimen de campo magnético que se elija, la función de filtrado de espín es evidente. Como se muestra en la Fig. 3a (Fig. 3b), solo los electrones de spin-up (spin-down) pueden fluir a través de la unión, mientras que la corriente de electrones con la otra dirección de spin se suprime totalmente a cero por la selectividad de spin del SMM en la dirección \ (+ S \) (\ (- S \)). Se obtienen resultados similares en la figura 3c, d cuando el campo magnético \ (\ Delta B \) se reduce a cero desde las direcciones \ (+ S \) y \ (- S \). En ausencia de \ (\ Delta B \), el SMM debe quedar atrapado en uno de los dos estados de tierra biestables \ (M =\ pm S \). Por esta razón, las direcciones de giro \ (+ S \) y \ (- S \) del SMM pueden conservarse bien en el régimen \ (\ Delta B =0 \). Por ejemplo, si escaneamos \ (\ Delta B \) desde \ (+ 5 \) meV a cero, se guarda \ (M =+ S \) y se obtiene una corriente de giro completamente polarizada (ver Fig. 3c ). Además, cuando aumenta el voltaje de polarización, la corriente de electrones en ausencia de un campo magnético externo alcanza una meseta de corriente relativamente alta antes que en el caso de un gran campo magnético. Como se muestra en la figura 3b, d, aunque no hay corrientes de giro en los regímenes \ (\ Delta B =0 \) meV y \ (\ Delta B =- \, 2 \) meV, el \ (I_ {\ flecha hacia abajo} \) las corrientes en la Fig. 3d pueden alcanzar hasta \ (0.5e \ Gamma _ {0} / \ hbar \) a \ (V \ approx 0.7 \) mV, mientras que para alcanzar la misma cantidad de corriente en Fig. 3c, se necesita un voltaje de polarización mayor de al menos \ (V> 1.5 \) mV.
Para aclarar la física subyacente en las Figs. 2 y 3, graficamos las probabilidades de estado molecular \ (P_ {| 0, \ pm S \ rangle} \), \ (P_ {| 0, S-1 \ rangle} \), \ (P_ {| 0, - S + 1 \ rangle} \), \ (P_ {| \ uparrow, S + 1/2 \ rangle} \), \ (P_ {| \ downarrow, -S-1/2 \ rangle} \), \ ( P_ {| 1, S-1/2 \ rangle} \) y \ (P_ {| 1, -S + 1/2 \ rangle} \) como funciones de \ (\ Delta B \) cuando se escanea el campo magnético hacia adelante y hacia atrás a una temperatura de equilibrio fija de \ (T =0.5 \) K y un voltaje de polarización de \ (V =1 \) mV. En la Fig. 4a, \ (\ Delta B \) se escanea desde \ (- 5 \) meV a \ (+ 5 \) meV lo suficientemente lento como para permitir que el sistema se relaje hasta el estado estable. Se muestra que en el régimen de campo magnético grande \ (\ Delta B <-2 \) meV, las probabilidades de todos los estados son iguales a cero excepto \ (P_ {| \ downarrow, -S-1/2 \ rangle} =1 \), lo que significa que el estado de giro del SMM está fijo en la dirección \ (- S \) y un electrón de giro hacia abajo queda atrapado en el nivel LUMO de la molécula por el campo magnético externo. Para un valor relativamente grande de la energía de repulsión de Coulomb (\ (U =25 \) meV) y un electrón de giro hacia abajo atrapado en el nivel LUMO, un electrón de giro no puede existir en el nivel del SMM y la corriente de electrones está bloqueada . Cuando \ (\ Delta B \) aumenta de \ (- 2 \) meV a 1 meV, surge una probabilidad de estado molecular distinta de cero \ (P_ {| 0, -S \ rangle} \), y la corriente de electrones está dominada por la \ (\ varepsilon _ {| 0, -S \ rangle} \ leftrightarrow \ varepsilon _ {| \ downarrow, -S-1/2 \ rangle} \) transición. En esta ventana \ (\ Delta B \), los estados de giro del SMM aún se pueden guardar en la dirección \ (- S \), pero los electrones de giro hacia abajo pueden hacer un túnel a través del SMM, lo que da como resultado una corriente de electrones polarizados de giro hacia abajo puro . Sin embargo, cuando \ (\ Delta B \) se incrementa aún más al rango de \ ([1 \, {\ text {meV}}, 2 \, {\ text {meV}}] \), los procesos de tunelización inelásticos que conducen a la conmutación magnética del giro de la molécula. En este régimen, casi todos los estados de espín del SMM tienen la posibilidad de estar ocupados, y las probabilidades de dos estados especiales, \ (P_ {| 0, -S \ rangle} \) y \ (P_ {| \ uparrow, + S + 1/2 \ rangle} \), son mucho más grandes que las de cualquier otro estado. Más interesante aún, el punto donde \ (P_ {| 0, -S \ rangle} =P_ {| \ uparrow, + S + 1/2 \ rangle} \) corresponde exactamente al punto \ (\ Lambda _ {+} \ ) en la Fig. 2a, lo que indica que la magnetización de la molécula está comenzando a revertirse de \ (- S \) a \ (+ S \). A medida que \ (\ Delta B \) continúa aumentando por encima de 2 meV, las probabilidades de todos los estados disminuyen a cero excepto \ (P_ {| \ uparrow, S + 1/2 \ rangle} \ rightarrow 1 \), lo que implica que los SMM El estado de giro se fija en la dirección \ (+ S \) y que la corriente de efecto túnel será "apagada" por un electrón de giro que bloquea el nivel LUMO de la molécula. Por otro lado, si el campo magnético se escanea desde \ (+ 5 \) meV a \ (- 5 \) meV (ver Fig. 4c), ocurrirá un proceso similar nuevamente, y el punto de inversión \ (\ Lambda _ {-} \) corresponde al punto donde \ (P_ {| 0, + S \ rangle} =P_ {| \ downarrow, -S-1/2 \ rangle} \). En la Fig. 4b, presentamos el diagrama de Zeeman para estos estados de espín. Debido a la gran anisotropía magnética del SMM, el doblete del estado fundamental con números cuánticos \ (M =\ pm S \) (\ (S =10 \) para \ (\ hbox {Mn} _ {{12}} \ ) -Ac) está bien separado de los estados excitados por una barrera de energía de \ (DS ^ {2} _ {z} \ approx 60 \) K. Además, el punto de conmutación magnético \ (\ Lambda _ {(+) - } \) en la Fig. 4 es aproximadamente igual a 1.3 meV, que está cerca del punto de inversión \ (2S | {\ mathcal {D}} | \) en átomos magnéticos individuales. En la figura 4d, graficamos las probabilidades del estado molecular como funciones del voltaje de polarización para una temperatura fija de \ (T =0.5 \) K y un campo magnético de \ (\ Delta B =0 \). Si asumimos que el SMM está atrapado en la dirección de giro \ (+ S \), entonces el proceso de tunelización de electrones en la figura 4d se puede dividir en dos partes:(i) En el régimen de pequeña polarización \ (V <2.5 \ ) MV, la corriente de electrones está dominada por la transición \ (\ varepsilon _ {| 0, + S \ rangle} \ leftrightarrow \ varepsilon _ {| \ uparrow, S + 1/2 \ rangle} \), y solo spin- los electrones pueden hacer un túnel a través de la unión. (ii) Cuando el voltaje de polarización aumenta al régimen de polarización grande \ (V> 2.5 \) mV, aunque la polarización no es lo suficientemente grande para superar la barrera de energía entre las direcciones de giro \ (+ S \) y \ (- S \), estados de giro con mayor energía en la dirección \ (+ S \), como \ (\ varepsilon _ {| 0, + S-1 \ rangle} \) y \ (\ varepsilon _ {| 1, + S -1/2 \ rangle} \), se puede ocupar, lo que introducirá canales adicionales adicionales para el túnel de electrones de spin-down a través del SMM. Como resultado, a medida que el voltaje de polarización continúa aumentando, la corriente de túnel seguirá creciendo, pero el coeficiente de polarización de espín \ (\ eta \) disminuirá.
Finalmente, los resultados para la corriente de giro \ (I _ {\ uparrow} \) y la corriente de giro hacia abajo \ (I _ {\ downarrow} \) como funciones del voltaje de la puerta (energía en el sitio del nivel LUMO \ ( \ varepsilon _ {0} \)) se calculan, con y sin un campo magnético externo (ver Fig. 5). Bajo temperaturas bajas, 100 \ (\% \) corrientes electrónicas con polarización de espín se pueden encender / apagar por medio de diferentes ventanas de voltaje de compuerta. Cuando se aplica \ (\ Delta B =\ pm 2 \) meV, las corrientes de spin puro - \ (\ sigma \) emergen en una cierta ventana de voltaje de puerta de \ (0.8 \, {\ text {meV}} <\ varepsilon _ {0} <2.8 \, {\ text {meV}} \), mientras que \ (I _ {\ uparrow} =I _ {\ downarrow} =0 \) fuera de este régimen. Como temperatura de equilibrio T aumenta, los picos de \ (I _ {\ sigma} \) bajan y se ensanchan, pero la alta corriente polarizada de espín que se observa a bajas temperaturas aún se mantiene (ver Fig. 5a, b). A diferencia del régimen de campo magnético grande, las corrientes de espín - \ (\ sigma \) se "encienden" sin un campo magnético externo en la ventana de voltaje de la puerta de \ (- 0.8 \, {\ text {meV}} <\ varepsilon _ {0} <1.8 \, {\ text {meV}} \), y la polarización de espín exhibe dos resultados diferentes (ver Fig. 5c, d). En la ventana de voltaje de la puerta de \ (0.8 \, {\ text {meV}} <\ varepsilon _ {0} <1.8 \, {\ text {meV}} \), \ (\ pm \, 100 \% \) Se pueden generar corrientes electrónicas con polarización de espín bajo una pequeña polarización de V \ (=1 \) mV, correspondiente a los puntos C y D de la figura 2c. Sin embargo, en la ventana de voltaje de puerta de \ (- 0.8 \, {\ text {meV}} <\ varepsilon _ {0} <0.8 \, {\ text {meV}} \), las brechas de energía entre los estados \ ( | 0, \ pm S \ rangle \) y \ (| 1, \ pm S \ mp 0.5 \ rangle \) se vuelven muy pequeños, y más estados de giro con mayor energía en \ (+ S \) (o \ (- S \)) la dirección de giro se puede alcanzar mediante la tensión de polarización; por lo tanto, tanto los electrones de espín hacia arriba como hacia abajo pueden hacer un túnel a través del SMM. En consecuencia, la polarización de espín total \ (\ eta \) de la corriente eléctrica se reduce en este régimen de voltaje de puerta.
Conclusión
En resumen, hemos propuesto un efecto de conmutación de tres estados con dos estados de "encendido" para la conmutación de corriente de giro hacia arriba y hacia abajo, así como un estado de corriente "apagado". Esta conmutación de corriente polarizada de espín se puede realizar en una unión de túnel SMM (por ejemplo, \ (\ hbox {Mn} _ {{12}} \) - Ac) y surge de la tunelización resonante de un solo electrón selectivo de espín a través del LUMO de el SMM. Este comportamiento de conmutación de tres estados se puede controlar mediante campos magnéticos y voltajes de compuerta, sin interacciones de espín-órbita o cables magnéticos, y es un buen candidato para dispositivos espintrónicos como filtros de espín o memorias de espín en futuros circuitos espintrónicos.
Disponibilidad de datos y materiales
Los conjuntos de datos utilizados durante el estudio actual están disponibles del autor correspondiente de este artículo.
Abreviaturas
- SMM:
-
Imán de molécula única
- LUMO:
-
Orbital molecular desocupado más bajo
- Mn 12 -Ac:
-
[Mn 12 O 12 (CH 3 CO 2 ) 15 (H 2 O) 4 ]
- TbPc 2 :
-
[(C 32 H 16 N 8 ) 2 Tb III ] complejo
Nanomateriales



