Un diseño eficiente y eficaz de nanocables de InP para la máxima captación de energía solar

Diseño para la máxima captación de luz de InP NWs

Las matrices InP NW alineadas verticalmente se colocan sobre un SiO ₂ semi-infinito sustrato como se muestra esquemáticamente en la Fig. 1 con una disposición cuadrada o hexagonal. Las celdas unitarias repetibles en los recuadros de la Fig. 1a, b explican las dimensiones de caracterización respectivas para cada disposición. Esta morfología y topología de las matrices NW están de acuerdo con la mayoría de las estructuras de células solares basadas en InP NW [11, 12, 23, 24]. Dentro de cada una de las celdas unitarias, los NW tienen el mismo o diferentes diámetros que D _i . Periodicidad p se define como la distancia de centro a centro de un par de NW adyacentes que tiene el mismo valor para NW dispuestos en escuadra, mientras que valores diferentes para matrices NW hexagonales. En consecuencia, el FR de las matrices NW ordenadas de forma cuadrada se define como \ (\ pi {\ sum} _ {\ mathrm {i} =1} ^ 4 {D_i} ^ 2 / {(4p)} ^ 2 \) que tiene el valor máximo de π / 4 cuando los NW ocupan el mayor porcentaje de volumen de la celda unitaria [25]. De manera similar, la FR para matrices NW hexagonales se define como \ (\ pi {\ sum} _ {\ mathrm {i} =1} ^ 2 {D_i} ^ 2 / \ left (4 \ sqrt {3} {p} ^ 2 \ right) \) con el valor máximo de \ (\ pi \ sqrt {3} / 6 \) [22]. La longitud l del NW se establece en 2 μm para todos los casos, ya que son lo suficientemente largos para absorber más del 90% de la energía incidente con un diseño adecuado [26].

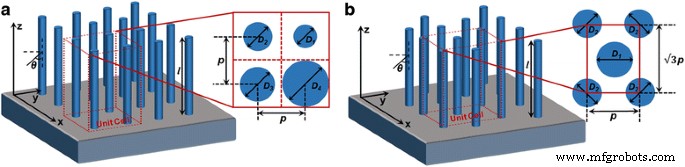
Esquemas de matrices InP NW alineadas verticalmente. un Squarely y b matrices NW hexagonales con recuadros que explican sus respectivas celdas unitarias

Para determinar analíticamente cada parámetro geométrico de las matrices de NW, el problema de optimización de múltiples parámetros para la máxima captación de luz se descompone en dos procesos:(1) control del modo resonante determinante del diámetro de NW y (2) reflectancia y transmitancia mínimas afectadas por FR de la energía solar incidente. Construimos la relación del parámetro geométrico individual con el proceso determinante respectivo e identificamos cada valor óptimo que conduce a la máxima absorción de luz. Las matrices NW de doble diámetro se eligen como ejemplo de diseño para ilustrar el método propuesto. Las dimensiones geométricas óptimas de las matrices NW de un solo diámetro como un caso más simple también se pueden adquirir durante la derivación. El diámetro y la periodicidad para matrices NW de cuatro diámetros también se pueden calcular como una extensión del ejemplo. Para matrices NW de diámetros dobles dispuestos en escuadra, los diámetros de las diagonales NW tienen el mismo valor que D _mayor y los diámetros de los otros dos NW se denominan D _{complementario} . Para matrices NW dispuestas hexagonales, el diámetro del centro NW es D _mayor y los diámetros de los NO en el periférico son D _{complementario} .

Se informa que las matrices NW pueden admitir modos de resonancia guiada / con fugas, cada uno de los cuales conduce a fuertes picos de absorción. Además, la naturaleza fundamental de la guía de ondas sugiere que el número de modo crece con el aumento del diámetro de NW. En consecuencia, el diámetro óptimo de NW debería ser lo suficientemente grande para soportar más modos para incluir un mayor número de resonancias de absorción. Sin embargo, los diámetros demasiado grandes de NW son menos preferibles ya que los modos de orden superior que soportan poseen más nodos que se acoplan de manera menos eficiente a las ondas planas incidentes [13]. Además, la propiedad del material y el espectro solar incidente imponen otras limitaciones a la selección del diámetro óptimo. Solo cuando los modos resonantes se encuentran dentro de la región de absorción, pueden contribuir a la fotocorriente. La región de absorción se define por la superposición del rango de absorción del material de hasta una longitud de onda crítica y el espectro incidente AM 1,5G [27].

Como resultado, para determinar cuantitativamente la D _mayor de las matrices NW, la resonancia en modo de fuga se adopta inicialmente para calcular las respectivas longitudes de onda resonantes para diferentes diámetros de NW [2]. Esto da la distribución de los modos resonantes en la región de absorción. Por lo tanto, la D óptima _mayor debe admitir dos modos para satisfacer todos los criterios anteriores. En segundo lugar, se adopta la teoría de Mie para calcular las eficiencias de absorción normalizadas de esos NW en el paso uno. Estrictamente hablando, la teoría de Mie no se puede aplicar a la situación en la que el vector de onda incidente se alinea perfectamente en paralelo al eje de NW, ya que la ecuación de valor propio está mal definida [28]. Sin embargo, esta situación puede aproximarse como el incidente del acristalamiento de la luz entrante (ángulo de incidencia muy pequeño θ con respecto al eje de NW) ya que en la interfaz de los arreglos NW, el frente de onda de la luz incidente será perturbado por el alto índice de NW que introduce componentes transversales al vector de onda permitiendo la adopción de la teoría de Mie [18]. Por lo tanto, la D óptima _mayor son los que admiten dos modos mientras mantienen el ancho completo a la mitad del máximo (FWHM) del modo resonante más bajo en el espectro de eficiencia de absorción normalizada dentro de la región de absorción. Después de la adquisición de D _mayor , la D _{complementario} se calcula con la condición de que los NW deben admitir un modo para reducir la reflexión y el ahorro de material y su longitud de onda resonante debe coincidir con el valle de la D _mayor Espectro de eficiencia de absorción normalizado.

La periodicidad de las matrices NW se puede calcular mediante la construcción de una capa de medio eficaz. Esta capa artificial representa el comportamiento de reflexión y transmisión de las matrices NW que solo está relacionado con el material FR. Como resultado, el diámetro, la periodicidad y la disposición de las matrices NW se eliminan del cálculo. De esta manera, la transmitancia y reflectancia de las matrices de NW se pueden evaluar aplicando ecuaciones de Fresnel en esta capa de medio efectivo y, por lo tanto, se puede analizar la FR óptima. Sobre la base de la relación de FR y periodicidad, se obtienen las periodicidades para matrices NW de disposición hexagonal y cuadrada. En las siguientes secciones se presenta una descripción detallada de nuestro método propuesto.

A. Diámetros óptimos de matrices InP NW para una máxima captación de luz

Para aumentar la absorción de luz, el número de modos resonantes que conducen a fuertes picos de absorción debe maximizarse dentro de la región de absorción. En el extremo azul de la región de absorción, el espectro de AM 1.5G incidente confina 300 nm como la región de alta energía. La longitud de onda crítica λ _c de 925 nm (banda prohibida de InP 1.34 eV) limita el extremo rojo de la región absorbente. Como resultado, se ha demostrado que los InP NW que admiten dos modos resonantes que se ubican dentro de la región absorbente son capaces de mejorar mejor la absorción de la luz [29]. Ampliamos esta conclusión y usamos la teoría de Mie para calcular el valor exacto.

Según la conclusión anterior, el rango de D _mayor se puede calcular a partir de la ecuación de valor propio derivada de las ecuaciones de Maxwell [18]. Teniendo en cuenta la distribución del campo antisimétrico en el plano de las ondas planas incidentes, solo el HE _1m los modos pueden excitarse eficazmente para contribuir a la absorción de NW alineados verticalmente [5]. Estos HE _1m Los modos satisfacen la ecuación de valor propio, y las longitudes de onda resonantes se pueden obtener asumiendo que la parte real de la constante de propagación Re (β _z ) del modo a lo largo de la dirección axial NW se aproxima a cero como se muestra en la Ec. (1). k _cilindro y k _aire son los componentes transversales del vector de onda dentro de los NW y en el aire, mientras que ε _cilindro y ε _aire son las respectivas permitividades. J ₁ y H ₁ ⁽¹⁾ son las funciones de Bessel y Hankel de primer orden del primer tipo. Como consecuencia, el rango en el que cae el diámetro primario se puede recibir con la condición de que el HE ₁₁ correspondiente y HE ₁₂ modo se encuentran dentro de la región absorbente.

Según la teoría de Mie, la eficiencia de absorción Q _abs de NW se define por la relación entre el área de recolección de energía y el tamaño geométrico de los NW. La expresión analítica de la eficiencia de absorción Q _abs se da a continuación, y el formalismo matemático exacto de la teoría de Mie se puede encontrar en la referencia [30]. Aquí, \ (\ overline {n} =n + ik \) es el índice de refracción complejo; como se mencionó anteriormente, J _i y H _i ⁽¹⁾ son las funciones de Bessel y Hankel de primer tipo de orden i .

Después de la adquisición de Q _abs del HE ₁₁ modo, se puede averiguar el FWHM del diámetro respectivo de los NW y, por lo tanto, se determina el diámetro óptimo para la máxima captación de luz. Tras la decisión del diámetro principal, el diámetro suplementario se confirma con la condición de que su longitud de onda máxima de absorción normalizada coincida con el valle de eficiencia de absorción normalizada del diámetro principal. Para las matrices NW de cuatro diámetros, el tercer y cuarto diámetros se determinan de manera similar. Sus picos de eficiencia de absorción normalizados deben coincidir con los valles de la superposición del espectro de eficiencia de absorción normalizado de los NW primarios y secundarios. Cabe señalar que, a excepción de los principales NW, se desea que el segundo, tercer y cuarto NW admitan solo un modo, ya que el tamaño de diámetro pequeño puede reducir la reflectancia en la interfaz aire-NW y reducir el consumo de material.

B. FR óptimo de las matrices InP NW para una máxima captación de luz

Varios trabajos publicados han revelado que con diámetros fijos de NW; la absorción de los NW aumentará con el FR inicialmente y luego disminuirá después de un cierto valor óptimo [13]. El aumento de la absorción de luz generalmente se atribuye al aumento del porcentaje de volumen de los materiales semiconductores con altos coeficientes de absorción. A medida que aumenta la FR, aumenta el índice de refracción medio de las matrices NW y, por tanto, aumenta la reflexión, lo que reduce la absorción de luz. Por lo tanto, se debe encontrar un límite superior en la FR para optimizar la influencia de la reflexión y transmisión de Fresnel para maximizar la absorción de las matrices NW. La figura 2 ilustra esquemáticamente que se crea una capa media eficaz de índice de refracción complejo para representar el comportamiento de refracción y transmisión de las matrices NW. De esta forma, las periodicidades y diámetros de NW se eliminan del cálculo. En consecuencia, el cálculo de Fresnel de la reflexión y la transmisión de la capa media efectiva se puede utilizar para reflejar las propiedades de las matrices NW. La naturaleza exacta dentro de esta capa de medio artificial no se considera siempre que puedan representar la reflexión y transmisión de matrices NW. Las derivaciones matemáticas detalladas se dan a continuación.

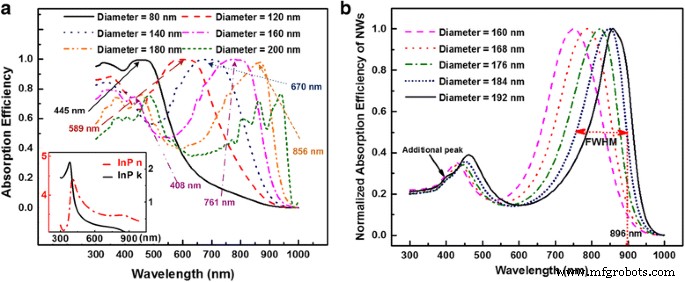
Reflexión, transmisión y absorción de luz de NW y capa media efectiva. un Arreglos InP NW y b la capa media efectiva correspondiente con el mismo grosor

La parte real del índice de refracción de la capa media efectiva n _{em_real} se determinan mediante la formulación de Bruggeman [31] en la Ec. (4) donde Ɛ _em y Ɛ _NW son la permitividad de la capa de medio eficaz e InP, respectivamente. La parte imaginaria del índice de refracción n _{em_imag} se calcula mediante la teoría del promedio de volumen [32, 33] en la ecuación. (5) donde n _{NW_real} , n _{NW_imag} , n _{air_real} y n _{air_imag} son la parte real e imaginaria del índice de refracción de NW y aire. El FR _opt óptimo se define como el FR tal que la absortancia Abs (λ) =1 - R (λ) - T (λ) se maximiza usando ecuaciones de Fresnel.

Al reemplazar las matrices NW con una película delgada de igual espesor, la reflectancia R (λ) y T (λ) La transmitancia de las matrices NW se puede estimar utilizando las ecuaciones de Fresnel. Los dos primeros términos de la serie infinita de reflexión y transmisión de Fabry-Perot se incluyen en la figura 2b. También se pueden encontrar derivaciones matemáticas detalladas en la información de apoyo de la referencia [13]. En esta etapa, se determinan los diámetros óptimos y el FR y se puede adquirir la periodicidad correspondiente en base a la definición del FR. Con las dimensiones geométricas óptimas, las matrices NW deberían conducir a la máxima absorción de luz. Densidad de corriente de cortocircuito J _sc se utiliza principalmente para medir la capacidad de captación de luz asumiendo que cada fotón absorbido conduce a una separación de excitones seguida de una colección de portadores exitosa. La definición se muestra en la ecuación. (6) donde A (λ) es la absorción dentro de los nanocables en función de la longitud de onda incidente, y N (λ) es el número de fotones por unidad de área por segundo para la longitud de onda incidente del espectro solar estándar.

Resultados y discusión

Los diámetros únicos y múltiples de matrices InP NW de arreglos cuadrados y hexagonales demuestran la validez del método propuesto. Mientras tanto, también se proporcionan simulaciones numéricas FDTD (Lumerical FDTD Solutions 8.15) para compararlas con nuestro método. La condición de límite periódica se aplica a lo largo de x y y ejes mientras que la condición de coincidencia perfecta se establece a lo largo de z eje como se ilustra en la Fig. 1. Los InP NW están colocados verticalmente sobre SiO ₂ sustrato. Las constantes ópticas para InP y SiO ₂ son de datos de material de Palik proporcionados por Lumerical. El espacio de parámetros para diámetros de NW varía de 50 a 200 nm, mientras que el FR es de 0.05 a los valores máximos posibles para NW cuadrados y hexagonales.

A. Aprovechamiento máximo de luz para InP NW de diámetro único

La Figura 3a muestra la eficiencia de absorción de luz para matrices de InP NW de diámetro único cuando FR es 0,05 con las constantes ópticas proporcionadas en el recuadro. Las respectivas longitudes de onda resonantes se calculan y marcan en los picos de absorción correspondientes que coinciden bien con los resultados de la simulación FDTD. El corrimiento al rojo de HE ₁₁ El modo resonante se puede observar fácilmente con el aumento del diámetro de NW. Además, tanto el cálculo como la simulación demuestran que el modo resonante evoluciona de uno a dos modos a 140 nm de diámetro. Por lo tanto, el valor óptimo para la absorción de luz máxima debería ser mayor que 140 nm y menor que 200 nm donde se excitan dos modos dentro de cada NW. Para encontrar el valor óptimo de diámetro, la eficiencia de absorción normalizada de las matrices NW se proporciona en la Fig. 3b que muestra las matrices NW que soportan dos modos y aún mantienen la FWHM dentro de la región de absorción. Por lo tanto, el valor más grande de 184 nm de diámetro se elige como el diámetro óptimo sin ningún pico adicional. Curiosamente, el diseño de celda solar InP NW de mayor eficiencia de conversión de energía actualizado adoptó el diámetro óptimo de 180 nm. Sus diámetros de NW se optimizaron experimentalmente en un rango de 50 a 300 nm con 10 nm como paso de aumento [9]. En comparación con nuestra predicción de 184 nm, una tolerancia estrecha de 4 nm demuestra la precisión de nuestro método.

Eficiencia de absorción dependiente de la longitud de onda de los InP NW y eficiencia de absorción normalizada. un Eficiencia de absorción de NW con recuadro que explica las constantes ópticas. b Eficiencia de absorción calculada por la teoría de Mie

La proporción de llenado se obtiene analíticamente usando una capa de medio eficaz en la sección B del método descrito. La eficiencia de absorción de luz de la capa efectiva de la misma altura que las matrices InP NW se muestra en la Fig. 4. En general, la capacidad de captación de luz aumenta inicialmente, alcanza su valor máximo y cae gradualmente a medida que la FR se acerca a un valor mayor. Esta tendencia se atribuye al cambio de la luz transmitida y reflejada a medida que cambian los índices de refracción complejos debido a la variación de FR. Específicamente, cuando FR aumenta de 0.05 a 0.2, debido a la adición de material InP, se absorbe más luz antes de transmitirse fuera de las matrices NW. Sin embargo, esta tendencia aumenta hasta que FR alcanza 0,2, y un aumento adicional de FR provoca un índice de refracción complejo alto de la capa equivalente que conduce a una impedancia óptica entre el aire y las matrices de NW. Como resultado, la reflectancia en la superficie incidente aumenta rápidamente, lo que disminuye la absorción de luz [13]. Por lo tanto, el valor óptimo para FR es 0.2 y las periodicidades para arreglos NW dispuestos en forma cuadrada y hexagonal son 364.63 y 391.82 nm, respectivamente.

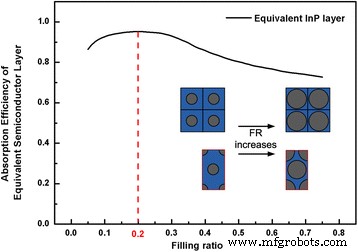
Eficiencia de absorción de la capa media eficaz para matrices InP NW en función de FR

Las densidades de corriente de cortocircuito para varias combinaciones de diámetros y FR se muestran en la Fig. 5. Demuestra claramente que la disposición de los NW tiene poco efecto sobre la absorción de luz más alta. Además, independientemente de las disposiciones de las matrices NW, nuestro método se puede aplicar y lograr resultados precisos. La J máxima _sc con las dimensiones geométricas óptimas calculadas para las matrices InP NW se calculan para la disposición cuadrada y hexagonal, respectivamente. El J máximo predicho analítico _sc es 32,11 y 32,06 mA / cm ² para matrices NW cuadradas y hexagonales que dan lugar a una tolerancia de 0,33 y 0,1%, respectivamente, en comparación con los resultados de la simulación FDTD.

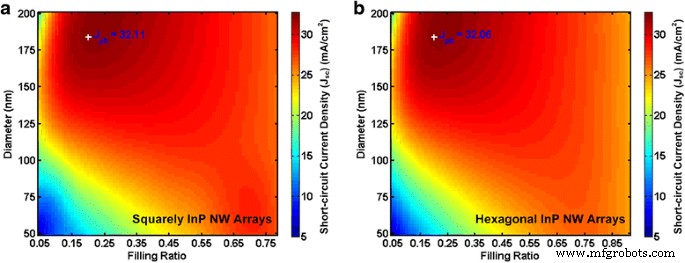
Valores máximos teóricos predichos en comparación con simulaciones FDTD. un Squarely y b matrices InP NW hexagonales de un solo diámetro

B. Cosecha máxima de luz para InP NW de doble diámetro

Varios grupos han investigado la adición de un diámetro secundario a las matrices NW para aumentar aún más la captación de energía solar [22, 29] mediante simulaciones que consumen mucho tiempo [34]. A partir de la discusión anterior, nuestro método proporciona una manera de aproximarnos rápidamente a los diámetros de NW requeridos. La longitud de onda resonante de los NW suplementarios debe coincidir con el valle de absorción del diámetro principal de los NW, que es de 585 nm, como se muestra en la Fig. 3b. Además, los NW deberían admitir solo un modo resonante. Estas dos conclusiones conducen a D _{complementario} de 119 nm. El FR óptimo de 0,2 sigue siendo válido en las matrices InP NW de doble diámetro, y la periodicidad se calcula como 307 y 329,95 nm para la disposición cuadrada y hexagonal de matrices NW. La Figura 6 proporciona una descripción general de la variación de las densidades de corriente de cortocircuito en función de D _mayor , D _{complementario} y FR para dos tipos de matrices NW. Generalmente, la cosecha de luz aumenta con FR, alcanza su valor máximo y cae. Cuando FR es 0.2, los recuadros de la Fig.6 muestran la J más alta _sc de 32,96 y 32,95 mA / cm ² tanto para InP NW cuadrados como hexagonales. Comparado con los valores máximos de simulaciones como 33,34 y 33,26 mA / cm ² , las tolerancias son 1,1 y 0,9% para NW cuadrados y hexagonales. La Figura 6 también muestra que a medida que crece FR, no se puede pasar por alto el acoplamiento entre los NW vecinos. La energía puede transferirse a los NW vecinos que soportan el mismo modo de fuga provocando la competencia de la energía incidente [35] que es perjudicial para la absorción de luz global. Cuando el FR es el mismo para ambos arreglos, p _cuadrado ² / p _hexagonal ² es \ (\ sqrt {3} / 2 \). Por lo tanto, la p _hexagonal es 1.08 veces la p _cuadrado que tiene menos acoplamiento de modo entre NW que las matrices cuadradas. Esto explica las diferencias de la recolección de luz de las dos matrices cuando FR es 0.05 y 0.4.

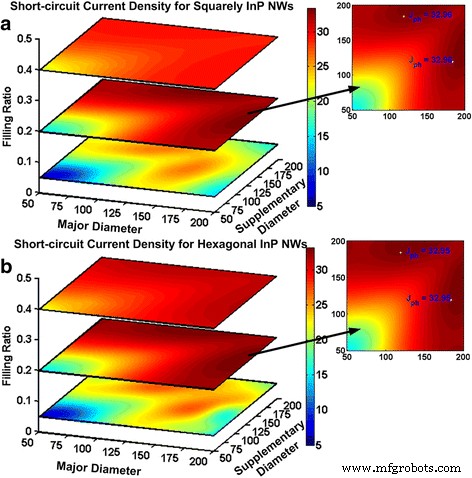
Densidades de corriente de cortocircuito en función de los diámetros principales, suplementarios y FR. un Squarely y b matrices hexagonales InP NW donde las inserciones muestran diámetros óptimos para las respectivas disposiciones NW

C. Aprovechamiento máximo de luz para InP NW de cuatro diámetros

Múltiples diámetros de matrices NW también atraen mucho interés de investigación para lograr una absorción cercana a la unidad en la región de absorción [29]. Sin embargo, solo se proporciona un número limitado de combinaciones de diámetros, ya que la adquisición de datos masivos requiere una gran cantidad de tiempo. Este problema se puede resolver en nuestro método de diseño analítico, y se proporcionan cuatro diámetros de matrices InP NW dispuestas en forma cuadrada como ejemplo. El tiempo total necesario para completar todos los cálculos utilizando nuestro método es igual al tiempo necesario para una sola simulación FDTD utilizando la misma computadora personal. Tras la adquisición de los diámetros mayor y complementario de NW, el tercer y cuarto diámetros de NW se pueden calcular de manera similar. La superposición de la eficiencia de absorción normalizada del diámetro principal y complementario de NW se muestra en la Fig. 7 con valles de absorción localizados en 486 y 704 nm. Por lo tanto, el tercer y cuarto diámetro de NW se puede calcular para satisfacer las condiciones de que cada uno de ellos admita solo un modo, y las longitudes de onda resonantes coincidan con los dos valles de absorción en la Fig. 7. En consecuencia, los diámetros tercero y cuarto para las matrices de InP NW se obtienen como 92 y 148 nm. Con el FR óptimo de 0.2 cuya validez es independiente de la disposición de NW y diámetros, la periodicidad se puede obtener como 277.41 nm para arreglos de InP NW.

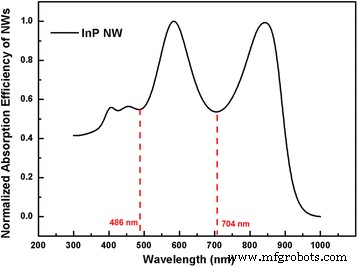
Superposition of the absorption efficiencies of the major and the supplementary diameters of InP NWs

The light absorption spectrum for the optimal combination of four NWs is provided in Fig. 8 from which the near-unity light absorption is achieved by the well selection of individual NWs. FDTD simulation results with four diameters’ combinations for squarely arranged NW arrays are shown in Fig. 9. To gain an overview of this multi-parameter optimization problem, two sets of coordinates are employed. The inner x and y axes denote the major and supplementary diameters whereas the outer x and y axes represent the third and fourth diameters. Due to the huge number of combinations of diameters, limited third and fourth diameters are deliberately selected to represent the whole absorption trend. From Fig. 3, the 80 nm is chosen as single mode resonance within NWs; 140 nm reflects the evolvement from single to double modes existence in NWs; 170 nm indicates the upper end of double modes existence while remain FWHM lying within absorbing region. Each intersect of the dash lines indicates different combination of the third and fourth diameters whereas the major and supplementary diameter run through 50 to 200 nm. When the diameters have larger values than 140 nm in Fig. 9, the majority of combinations of diameters will lead to the J _sc above 30 mA/cm ² . When all of the diameters reach above 170 nm, the average of J _sc can be 32 mA/cm ² . These results are also reflected in Figs. 5a and 6a. Compared with single or double diameter NW arrays, optimized four diameter NW arrays indeed lead to higher J _sc . The highest J _sc for four diameters InP NW arrays with our calculated geometrical dimensions is 33.13 mA/cm ² with a tolerance of 2.2%.

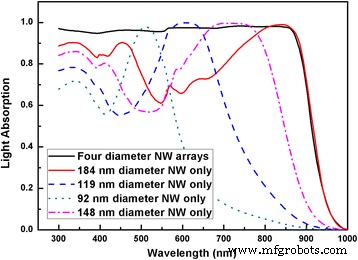
Light absorption of four diameter InP NW arrays

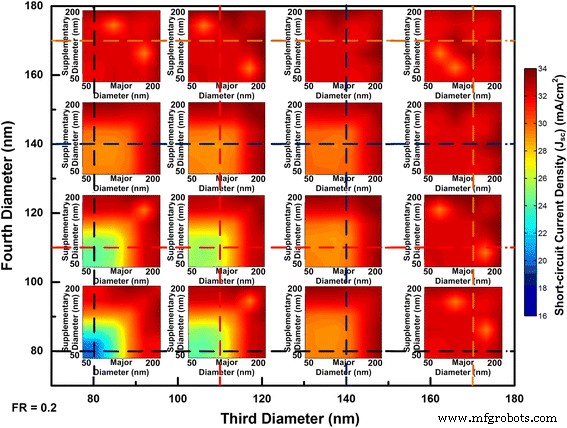
Short-circuit current densities change with the major, supplementary, third, and fourth InP NWs

Conclusiones

In this study, we present model for effective and fast design of both squarely and hexagonal InP NW arrays to achieve the highest light harvesting for photovoltaic application. Geometrical dimensions for vertically aligned single, double, and multiple diameters of NW arrays are investigated. Compared with time-consuming FDTD simulations, our predicted maximal short-circuit current densities with calculated three-dimensional NW arrays remain tolerances below 2.2% for all cases. For single diameter NW arrays, the optimal diameter is 184 nm which is only 4 nm difference to the reported highest efficiency InP NW solar cells. In the multiple diameter NW arrays, the diameters of the rest of NWs are optimized to satisfy the conditions that they support only one resonant mode and the corresponding wavelengths match the absorption valley of the major NWs. Moreover, the FR of the NW array is optimized to be 0.2 by creating an effective medium layer which is regardless of the diameter, periodicity, and arrangements of NWs. Compared with the optical modeling, the predicted highest short-circuit current densities for single diameter NW arrays lie within 0.33 and 0.1% tolerance for squarely and hexagonal NW array. The arrangements of NW array have little influence on the light absorption with optimal geometrical parameters, but the coupling among neighboring NWs becomes serious for multiple diameter NWs at large FR value. Squarely arranged four diameter NW arrays were also presented and the highest short-circuit current densities predicted to be 33.13 mA/cm ² with a low tolerance of 2.2%. The time-efficient, high precision with wide suitability of the proposed design for InP NW arrays demonstrate itself to be a promising tool to guide practical NW-based solar cell design.

Abreviaturas

FDTD:

Dominio del tiempo de diferencia finita

FR:

Filling ratio

FWHM:

Ancho completo a la mitad del máximo

NPs:

Nanopartículas

NWs:

Nanowires

Rendimiento mejorado de un nuevo catalizador anódico de PdAu / VGCNF para la electrooxidación en una pila de combustible de glicerol Respuesta fotovoltaica pronunciada del fototransistor MoTe2 multicapa con formulario de contacto asimétrico