Solución Minterm vs Maxterm

Hasta ahora hemos estado encontrando soluciones de suma de producto (SOP) para problemas de reducción lógica. Para cada una de estas soluciones SOP, también existe una solución de Producto de Sumas (POS), que podría ser más útil, dependiendo de la aplicación.

Antes de trabajar en una solución de producto de sumas, debemos introducir una nueva terminología. El siguiente procedimiento para mapear términos de productos no es nuevo en este capítulo.

Solo queremos establecer un procedimiento formal para minitérminos para compararlo con el nuevo procedimiento para maxterms.

Minitérmino

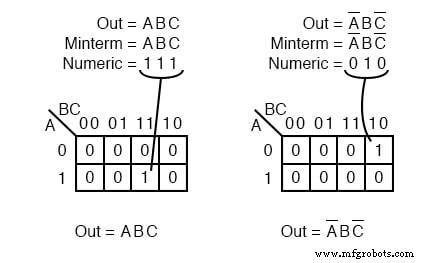
Un término mínimo es una expresión booleana que da como resultado 1 para la salida de una sola celda y 0 s para todas las demás celdas de un mapa de Karnaugh o tabla de verdad. Si un minitérmino tiene un solo 1 y las celdas restantes como 0 s, parecería cubrir un área mínima de 1 s.

La ilustración de arriba a la izquierda muestra el término mínimo ABC , un solo término de producto, como un solo 1 en un mapa que de otro modo es 0 s. No hemos mostrado el 0 s en nuestros mapas de Karnaugh hasta este punto, ya que es costumbre omitirlos a menos que sea específicamente necesario. Otro término mínimo A’BC ’ se muestra arriba a la derecha.

El punto a revisar es que la dirección de la celda corresponde directamente al minitérmino que se está mapeando. Es decir, la celda 111 corresponde al minitérmino ABC arriba a la izquierda.

Arriba a la derecha vemos que el minitérmino A’BC ’ corresponde directamente a la celda 010 . Una expresión o mapa booleano puede tener varios términos mínimos.

Con referencia a la figura anterior, resumamos el procedimiento para colocar un término mínimo en un mapa K:

• Identifique el término mínimo (término del producto) que se va a asignar.
• Escriba el valor numérico binario correspondiente.
• Utilice un valor binario como dirección para colocar un 1 en el K-map
• Repita los pasos para otros términos mínimos (términos P dentro de una suma de productos).

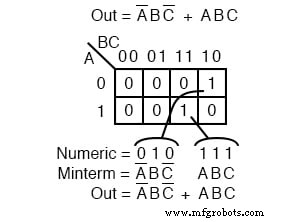
Una expresión booleana a menudo constará de múltiples términos mínimos correspondientes a múltiples celdas en un mapa de Karnaugh como se muestra arriba. Los múltiples términos mínimos en este mapa son los términos mínimos individuales que examinamos en la figura anterior anterior.

El punto que revisamos como referencia es que el 1 s salen del mapa K como una dirección de celda binaria que se convierte directamente en uno o más términos de producto.

Por directamente queremos decir que un 0 corresponde a una variable complementada y un 1 corresponde a una verdadera variable. Ejemplo: 010 convierte directamente a A’BC ’ .

No hubo reducción en este ejemplo. Sin embargo, tenemos un resultado de suma de productos a partir de los términos mínimos.

Con referencia a la figura anterior, resumamos el procedimiento para escribir la ecuación booleana reducida de suma de productos a partir de un mapa K:

• Forme grupos más grandes de 1 Es posible cubrir todos los términos mínimos. Los grupos deben tener una potencia de 2.
• Escriba un valor numérico binario para grupos.
• Convierta un valor binario en un término de producto.
• Repita los pasos para otros grupos. Cada grupo produce términos p dentro de una suma de productos.

Nada nuevo hasta ahora, se ha redactado un procedimiento formal para tratar los minitérminos. Esto sirve como patrón para tratar con términos máximos.

A continuación atacamos la función booleana que es 0 para una sola celda y 1 s para todos los demás.

Maxterm

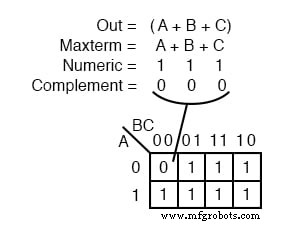
Un maxterm es una expresión booleana que da como resultado un 0 para la salida de una expresión de celda única y 1 s para todas las demás celdas del mapa de Karnaugh o tabla de verdad. La ilustración de arriba a la izquierda muestra el término máximo (A + B + C) , un término de suma única, como un solo 0 en un mapa que de otro modo es 1 s.

Si un maxterm tiene un solo 0 y las celdas restantes como 1 s, parecería cubrir un área máxima de 1 s.

Hay algunas diferencias ahora que estamos tratando con algo nuevo, maxterms. El maxterm es un 0 , no un 1 en el mapa de Karnaugh. Un término máximo es un término de suma, (A + B + C) en nuestro ejemplo, no es un término de producto. También parece extraño que (A + B + C) se asigna a la celda 000 .

Para la ecuación Fuera =(A + B + C) =0 , las tres variables (A, B, C) debe ser individualmente igual a 0 . Solo (0 + 0 + 0) =0 será igual a 0 . Así colocamos nuestra suela 0 para el término mínimo (A + B + C) en la celda A, B, C =000 en el mapa K, donde las entradas son todas 0 .

Este es el único caso que nos dará un 0 para nuestro maxterm. Todas las demás celdas contienen 1 s porque cualquier valor de entrada que no sea ( (0,0,0) para (A + B + C) produce 1 s tras la evaluación.

Con referencia a la figura anterior, el procedimiento para colocar un término máximo en el mapa K es:

• Identifique el término de suma que se va a asignar.
• Escriba el valor numérico binario correspondiente.
• Forme el complemento
• Utilice el complemento como dirección para colocar un 0 en el K-map
• Repita para otros términos máximos (términos de suma dentro de la expresión Producto de sumas).

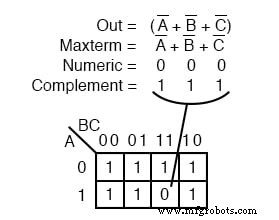
Otro término máximo A ’+ B’ + C ’ se muestra arriba. 000 numérico corresponde a A ’+ B’ + C ’ . El complemento es 111 . Coloque un 0 para maxterm (A ’+ B’ + C ’) en esta celda (1,1,1) del mapa K como se muestra arriba.

¿Por qué (A ’+ B’ + C ’) causar un 0 estar en la celda 111 ? Cuando A ’+ B’ + C ’ es (1 ’+ 1’ + 1 ’) , todos 1 s en, que es (0 + 0 + 0) después de tomar complementos, tenemos la única condición que nos dará un 0 . Todo el 1 Los correos electrónicos se complementan con todos los 0 s, que es 0 cuando O ed.

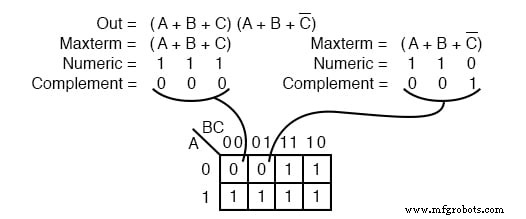
Una expresión o mapa booleano de producto de sumas puede tener varios términos máximos, como se muestra arriba. Maxterm (A + B + C) produce 111 numéricos que complementa a 000 , colocando un 0 en la celda (0,0,0) . Maxterm (A + B + C ’) produce 110 numéricos que complementa a 001 , colocando un 0 en la celda (0,0,1) .

Ahora que tenemos la configuración del mapa k, lo que realmente nos interesa es mostrar cómo escribir una reducción de producto de sumas. Forma el 0 s en grupos. Eso sería un grupo de dos a continuación. Escribe el valor binario correspondiente al término suma que es (0,0, X) .

Tanto A como B son 0 para el grupo. Pero, C es tanto 0 y 1 entonces escribimos una X como marcador de posición para C . Forma el complemento (1,1, X) . Escribe el término de suma (A + B) descartando la C y la X que ocupó su lugar.

En general, espere tener más términos de suma multiplicados en el resultado del producto de las sumas. Sin embargo, tenemos un ejemplo simple aquí.

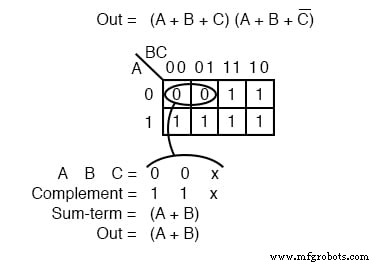
Resumamos el procedimiento para escribir la reducción booleana del producto de sumas para un mapa K:

• Forme grupos más grandes de 0 s posible, cubriendo todos los maxterms. Los grupos deben tener una potencia de 2.
• Escriba un valor numérico binario para el grupo.
• Complemente el valor numérico binario para el grupo.
• Convierta el valor del complemento en un término de suma.
• Repita los pasos para otros grupos. Cada grupo produce un término de suma dentro de un resultado de producto de sumas.

Ejemplos

Ejemplo:

Simplifique la expresión booleana Producto de sumas a continuación, proporcionando un resultado en forma de POS.

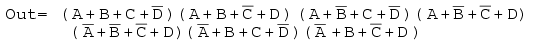
Solución:

Transfiera los siete términos máximos al mapa siguiente como 0 s. Asegúrese de complementar las variables de entrada para encontrar la ubicación adecuada de la celda.

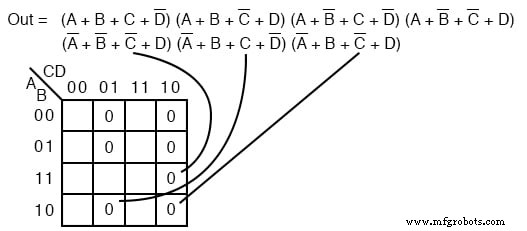
Mapeamos el 0 s como aparecen de izquierda a derecha de arriba a abajo en el mapa de arriba. Localizamos los últimos tres términos máximos con líneas guía.

Una vez que las celdas estén en su lugar arriba, forme grupos de celdas como se muestra a continuación. Los grupos más grandes darán un término de suma con menos entradas. Menos grupos producirán menos términos de suma en el resultado.

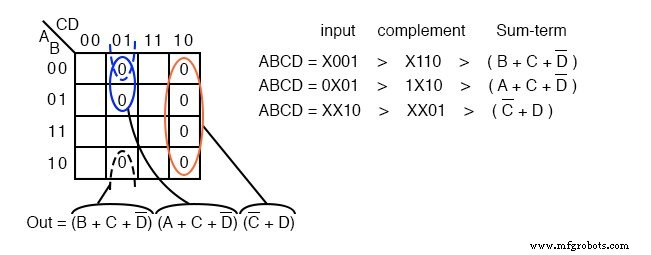
Tenemos tres grupos, por lo que esperamos tener tres términos de suma en nuestro resultado POS anterior. El grupo de 4 celdas produce un término de suma de 2 variables. Los dos grupos de 2 celdas nos dan dos términos de suma de 3 variables.

Se muestran detalles de cómo llegamos a los términos de suma anteriores. Para un grupo, escriba la dirección de entrada del grupo binario, luego complétela, convirtiéndola en el término suma booleano. El resultado final es el producto de las tres sumas.

Ejemplo:

Simplifique la expresión booleana Producto-de-Sumas a continuación, proporcionando un resultado en forma de SOP.

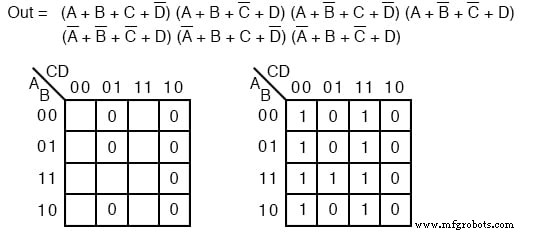
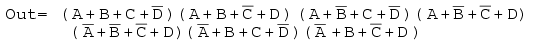
Solución: Esto parece una repetición del último problema. Excepto que pedimos una solución de suma de productos en lugar del producto de sumas que acabamos de terminar. Asignar el maxterm 0 s del Producto-de-Sumas dado como en el problema anterior, abajo a la izquierda.

Luego, complete el 1 implícito s en las celdas restantes del mapa arriba a la derecha.

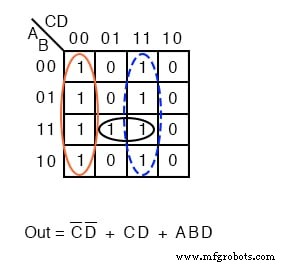
Formar grupos de 1 s para cubrir todos 1 s. Luego, escriba el resultado simplificado de la suma de productos como en la sección anterior de este capítulo. Esto es idéntico a un problema anterior.

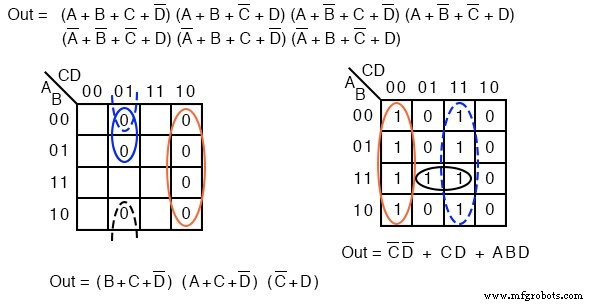
Arriba mostramos tanto la solución Producto-de-Sumas, del ejemplo anterior, como la solución Suma-de-Productos del problema actual para comparar.

Cual es la solucion mas simple? El POS usa puertas 3-OR y una puerta 1-Y, mientras que el SOP usa puertas 3-Y y una puerta 1-OR. Ambos usan cuatro puertas cada uno.

Echando un vistazo más de cerca, contamos el número de entradas de puerta. El POS utiliza 8 entradas; el SOP utiliza 7 entradas. Según la definición de solución de costo mínimo, la solución SOP es más simple.

Este es un ejemplo de una respuesta técnicamente correcta que es de poca utilidad en el mundo real.

La mejor solución depende de la complejidad y de la familia lógica que se utilice. La solución SOP suele ser mejor si se utiliza la familia lógica TTL, ya que las puertas NAND son el bloque de construcción básico, que funciona bien con las implementaciones SOP.

Por otro lado, una solución POS sería aceptable cuando se usa la familia lógica CMOS ya que todos los tamaños de puertas NOR están disponibles.

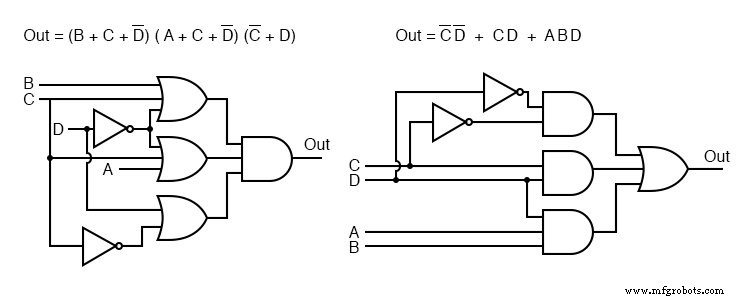
Los diagramas de puerta para ambos casos se muestran arriba, Producto de sumas a la izquierda y Suma de productos a la derecha.

A continuación, echamos un vistazo más de cerca a la versión de suma de productos de nuestra lógica de ejemplo, que se repite a la izquierda.

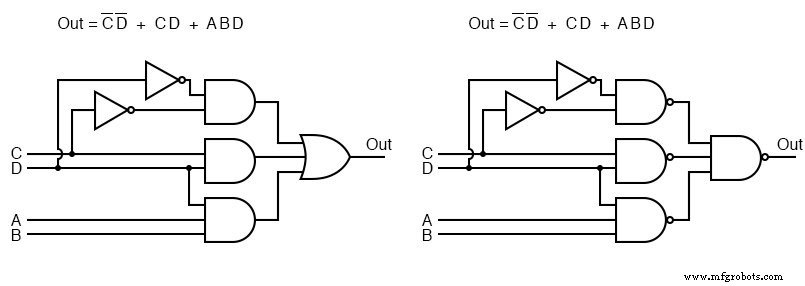
Sobre todo, las puertas Y a la izquierda han sido reemplazadas por puertas NAND a la derecha. La puerta O en la salida es reemplazada por una puerta NAND. Para probar que la lógica AND-OR es equivalente a la lógica NAND-NAND, mueva las burbujas invertidas del inversor en la salida de las puertas 3-NAND a la entrada de la NAND final como se muestra al ir de arriba a la derecha a abajo a la izquierda.

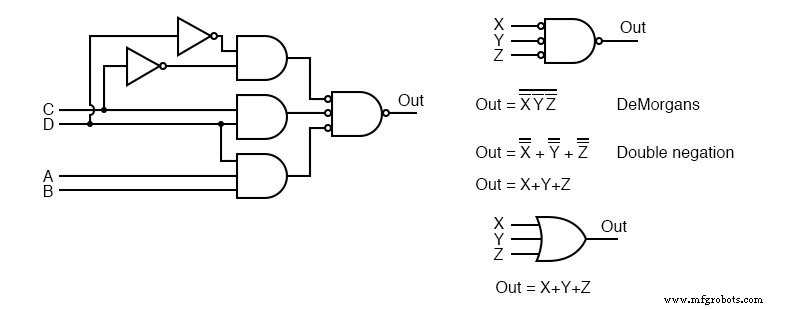
Arriba a la derecha vemos que la puerta NAND de salida con entradas invertidas es lógicamente equivalente a una puerta OR según el teorema de DeMorgan y la doble negación.

Esta información es útil para crear lógica digital en un entorno de laboratorio donde las puertas NAND de la familia lógica TTL están más disponibles en una amplia variedad de configuraciones que otros tipos.

El procedimiento para construir la lógica NAND-NAND, en lugar de la lógica AND-OR, es el siguiente:

• Producir un diseño lógico de suma de productos reducido.
• Al dibujar el diagrama de cableado del SOP, reemplace todas las puertas (tanto Y como O) por puertas NAND.
• Las entradas no utilizadas deben estar vinculadas a la lógica alta.
• En caso de resolución de problemas, los nodos internos en el primer nivel de las salidas de la puerta NAND NO coinciden con los niveles lógicos del diagrama Y-O, sino que están invertidos. Utilice el diagrama lógico NAND-NAND. Sin embargo, las entradas y la salida final son idénticas.
• Etiquete los paquetes múltiples U1, U2, .. etc.
• Use la hoja de datos para asignar números de pines a las entradas y salidas de todas las puertas.

Ejemplo:

Repasemos un problema anterior que involucraba una minimización de POE. Genere una solución de producto de sumas. Compare la solución POS con el SOP anterior.

Solución:

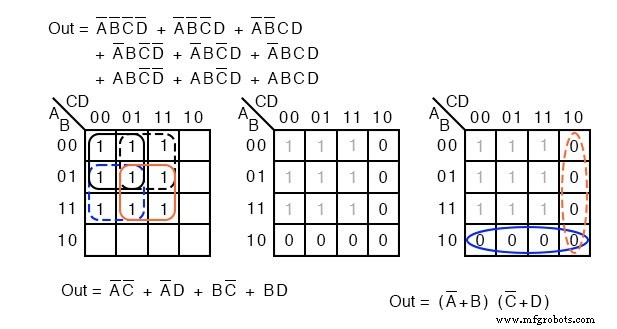
Arriba a la izquierda tenemos el problema original que comienza con una expresión booleana no simplificada de 9 minutos. Al revisar, formamos cuatro grupos de 4 celdas para producir un resultado de SOP de término de 4 productos, abajo a la izquierda.

En la figura del medio, arriba, llenamos los espacios vacíos con el 0 implícito s. El 0 s forman dos grupos de 4 celdas. El grupo azul sólido es (A ’+ B) , el grupo rojo punteado es (C ’+ D) . Esto produce dos términos de suma en el resultado del producto de las sumas, arriba a la derecha Fuera =(A ’+ B) (C’ + D)

Comparando la simplificación de SOP anterior, izquierda, con la simplificación POS, derecha, muestra que POS es la solución de menor costo. El SOP usa 5 puertas en total, el POS usa solo 3 puertas.

Esta solución POS incluso se ve atractiva cuando se usa la lógica TTL debido a la simplicidad del resultado. Podemos encontrar puertas AND y una puerta OR con 2 entradas.

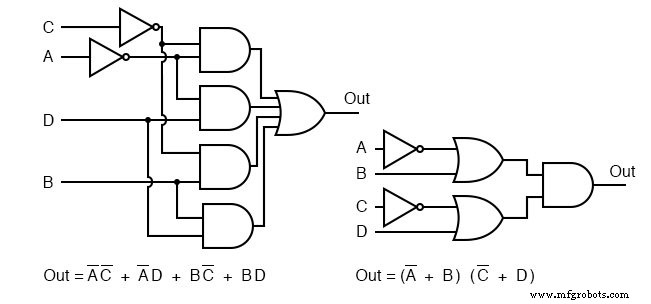
Los diagramas de puertas de POS y SOP se muestran arriba para nuestro problema de comparación.

Dados los pines para las puertas de circuito integrado de la familia lógica TTL a continuación, etiquete el diagrama de maxterm arriba a la derecha con designadores de circuito (U1-a, U1-b, U2-a, etc.) y números de pin.

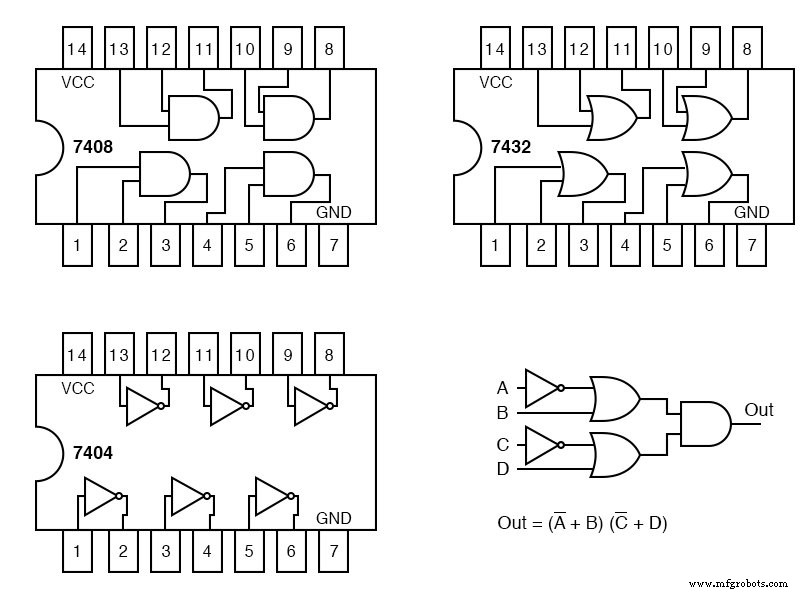
Cada paquete de circuito integrado que usemos recibirá un designador de circuito:U1, U2, U3. Para distinguir entre las puertas individuales dentro del paquete, se identifican como a, b, c, d, etc.

El paquete de inversor hexagonal 7404 es U1. Los inversores individuales en él son U1-a, U1-b, U1-c, etc. U2 se asigna a la puerta OR 7432 quad. U3 está asignado a la puerta Y cuádruple 7408.

Con referencia a los números de pin en el diagrama del paquete anterior, asignamos números de pin a todas las entradas y salidas de puerta en el diagrama esquemático a continuación.

Ahora podemos construir este circuito en un laboratorio. O podríamos diseñar una placa de circuito impreso para ello. Una placa de circuito impreso contiene un "cableado" de lámina de cobre respaldado por un sustrato no conductor de fibra de vidrio fenólica o epoxi.

Las placas de circuito impreso se utilizan para producir circuitos electrónicos en masa. Conecte a tierra las entradas de las puertas no utilizadas.

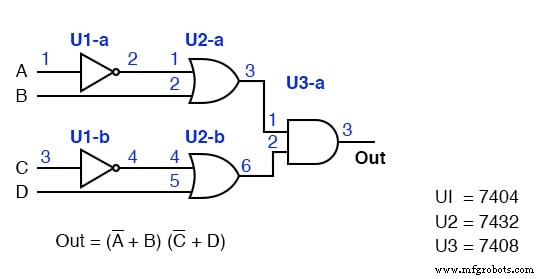
Etiquete el diagrama de solución POS anterior arriba a la izquierda (tercera figura atrás) con designadores de circuito y números de pin. Esto será similar a lo que acabamos de hacer.

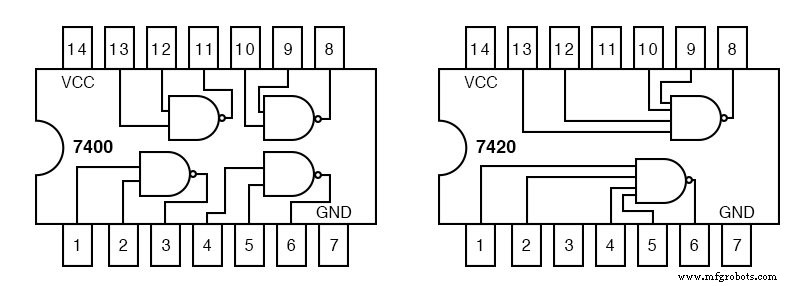
Podemos encontrar puertas AND de 2 entradas, 7408 en el ejemplo anterior. Sin embargo, tenemos problemas para encontrar una puerta OR de 4 entradas en nuestro catálogo TTL.

El único tipo de puerta con 4 entradas es la puerta NAND 7420 que se muestra arriba a la derecha.

Podemos convertir la puerta NAND de 4 entradas en una puerta OR de 4 entradas invirtiendo las entradas a la puerta NAND como se muestra a continuación. Entonces usaremos la puerta NAND de 4 entradas 7420 como una puerta OR invirtiendo las entradas.

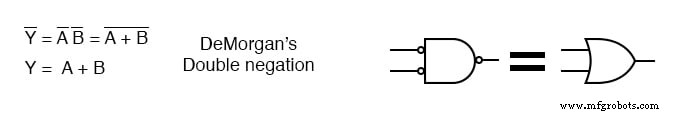
No usaremos inversores discretos para invertir las entradas a la compuerta NAND de 4 entradas 7420, pero la manejaremos con compuertas NAND de 2 entradas en lugar de las compuertas AND solicitadas en la solución SOP, minterm.

La inversión en la salida de las puertas NAND de 2 entradas proporciona la inversión para la puerta OR de 4 entradas.

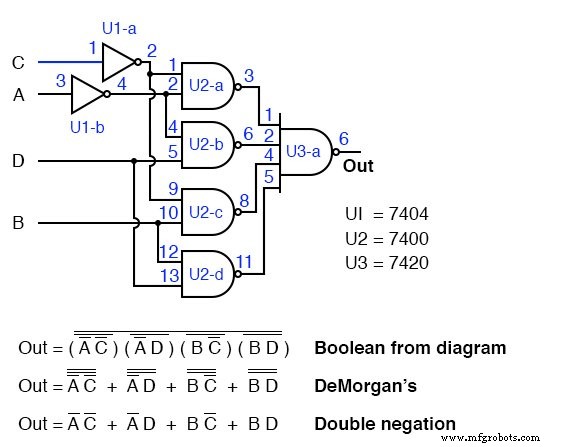
El resultado se muestra arriba. Es la única forma práctica de construirlo con puertas TTL usando la lógica NAND-NAND reemplazando la lógica AND-OR.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de mapeo de Karnaugh