Conversión de tablas de verdad en expresiones booleanas

Al diseñar circuitos digitales, el diseñador a menudo comienza con una tabla de verdad que describe lo que debería hacer el circuito.

La tarea de diseño consiste principalmente en determinar qué tipo de circuito realizará la función descrita en la tabla de verdad.

Si bien algunas personas parecen tener una capacidad natural para mirar una tabla de verdad e imaginar inmediatamente la puerta lógica necesaria o los circuitos lógicos de relé para la tarea, existen técnicas de procedimiento disponibles para el resto de nosotros.

Aquí, el álgebra de Boole demuestra su utilidad de la manera más dramática.

Para ilustrar este método de procedimiento, debemos comenzar con un problema de diseño realista.

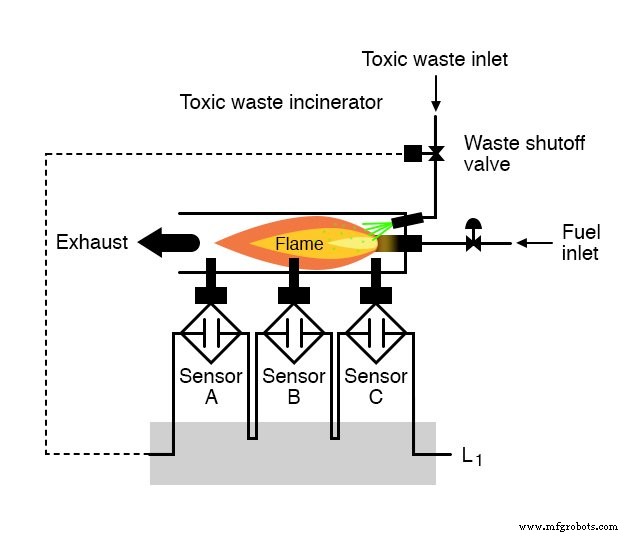
Supongamos que se nos encomienda la tarea de diseñar un circuito de detección de llamas para un incinerador de desechos tóxicos.

El intenso calor del fuego tiene como objetivo neutralizar la toxicidad de los residuos introducidos en el incinerador.

Estas técnicas basadas en la combustión se utilizan comúnmente para neutralizar los desechos médicos, que pueden estar infectados con virus o bacterias mortales:

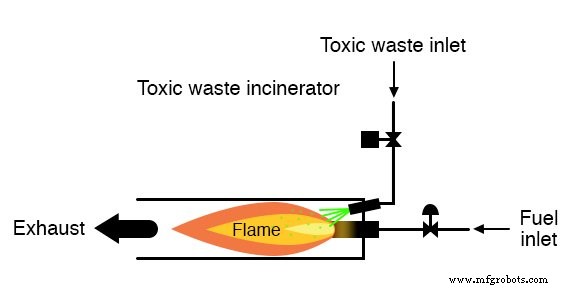
Siempre que se mantenga una llama en el incinerador, es seguro inyectarle desechos para neutralizarlo.

Sin embargo, si la llama se extinguiera, no sería seguro continuar inyectando desechos en la cámara de combustión, ya que saldría del escape sin neutralizar y representaría una amenaza para la salud de cualquier persona que se encuentre cerca del escape.

Lo que necesitamos en este sistema es una forma segura de detectar la presencia de una llama y permitir que los desechos se inyecten solo si el sistema de detección de llama "prueba" una llama.

Existen varias tecnologías diferentes de detección de llama:óptica (detección de luz), térmica (detección de alta temperatura) y conducción eléctrica (detección de partículas ionizadas en el camino de la llama), cada una con sus ventajas y desventajas únicas.

Suponga que debido al alto grado de peligro involucrado con el paso potencial de desechos no neutralizados por el escape de este incinerador, se decide que el sistema de detección de llama sea redundante (sensores múltiples), de modo que la falla de un solo sensor no conduzca a una emisión de toxinas por los gases de escape.

Cada sensor viene equipado con un contacto normalmente abierto (abierto si no hay llama, cerrado si se detecta llama) que usaremos para activar las entradas de un sistema lógico:

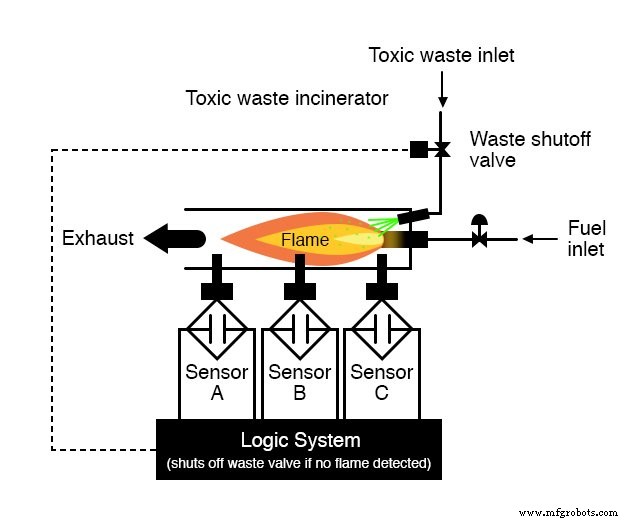
Nuestra tarea, ahora, es diseñar los circuitos del sistema lógico para abrir la válvula de desperdicio si y solo si hay una buena llama probada por los sensores.

Sin embargo, primero debemos decidir cuál debería ser el comportamiento lógico de este sistema de control.

¿Queremos que se abra la válvula si solo uno de los tres sensores detecta llama? Probablemente no, porque esto frustraría el propósito de tener múltiples sensores.

Si alguno de los sensores fallara de tal manera que indicara falsamente la presencia de llama cuando no había ninguna, un sistema lógico basado en el principio de "cualquiera de los tres sensores que muestren llama" daría la misma salida que un sistema de sensor único tendría el mismo fallo.

Una solución mucho mejor sería diseñar el sistema de modo que se ordene a la válvula que se abra si y solo si los tres sensores detectar una buena llama.

De esta manera, cualquier sensor que fallara y mostrara una llama falsamente no podría mantener la válvula en la posición abierta; más bien, se requeriría que los tres sensores fallaran de la misma manera (un escenario altamente improbable) para que ocurra esta peligrosa condición.

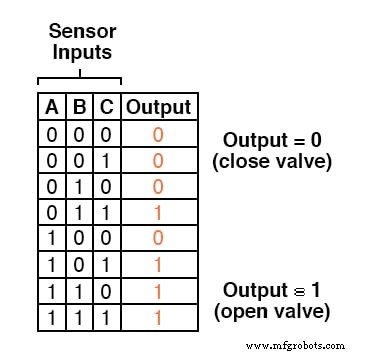
Por lo tanto, nuestra tabla de verdad se vería así:

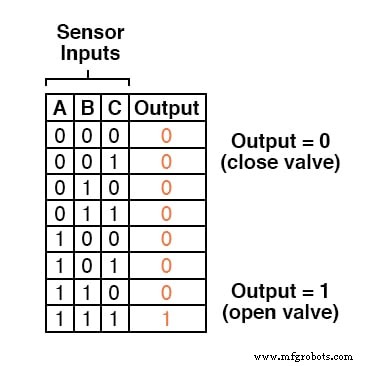
No se requiere mucha información para darse cuenta de que esta funcionalidad podría generarse con una puerta AND de tres entradas:la salida del circuito será "alta" si y solo si la entrada A AND entrada B Y la entrada C son todas "altas":

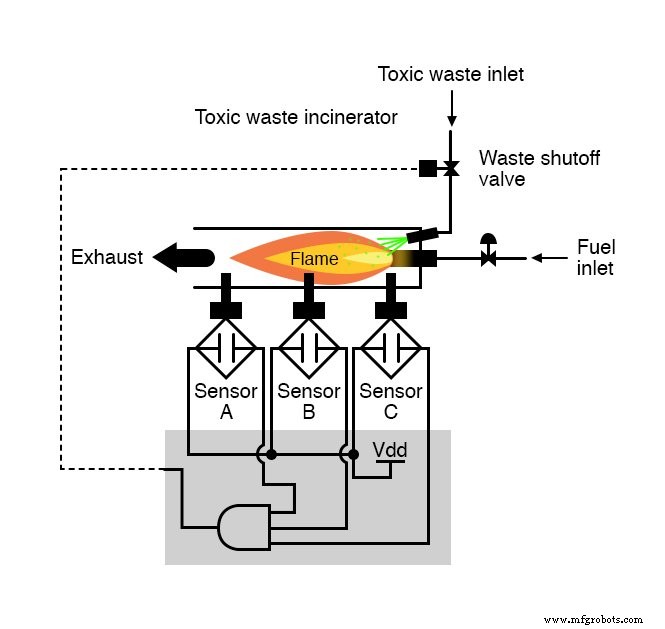
Si usamos circuitos de relé, podríamos crear esta función Y cableando tres contactos de relé en serie, o simplemente cableando los tres contactos de sensor en serie, de modo que la única forma en que se pueda enviar energía eléctrica para abrir la válvula de desperdicio sea si los tres sensores indicar llama:

Si bien esta estrategia de diseño maximiza la seguridad, hace que el sistema sea muy susceptible a fallas de sensores del tipo opuesto.

Supongamos que uno de los tres sensores fallara de tal manera que indicara que no hay llama cuando realmente hay una buena llama en la cámara de combustión del incinerador.

Esa sola falla cerraría la válvula de desperdicio innecesariamente, resultando en pérdida de tiempo de producción y combustible desperdiciado (alimentando un fuego que no se estaba usando para incinerar desperdicios).

Sería bueno tener un sistema lógico que permitiera este tipo de falla sin apagar el sistema innecesariamente, y aún así proporcionar redundancia del sensor para mantener la seguridad en caso de que un solo sensor fallara "alto" (mostrando la llama en todo momento , si había uno para detectar o no).

Una estrategia que satisfaría ambas necesidades sería una lógica de sensor "dos de tres", mediante la cual la válvula de desechos se abre si al menos dos de los tres sensores muestran una buena llama.

La tabla de verdad para un sistema de este tipo se vería así:

Uso de la suma de productos

Aquí, no es necesariamente obvio qué tipo de circuito lógico satisfaría la tabla de verdad.

Sin embargo, un método simple para diseñar un circuito de este tipo se encuentra en una forma estándar de expresión booleana llamada Suma de productos o SOP , formulario.

Como puede sospechar, una expresión booleana de suma de productos es literalmente un conjunto de términos booleanos agregados ( sumados ) juntos, siendo cada término un ( producto ) combinación de variables booleanas.

Un ejemplo de una expresión SOP sería algo como esto:ABC + BC + DF, la suma de los productos "ABC", "BC" y "DF".

Las expresiones de suma de productos son fáciles de generar a partir de tablas de verdad.

Todo lo que tenemos que hacer es examinar la tabla de verdad para cualquier fila donde la salida sea "alta" (1) y escribir un término de producto booleano que equivaldría a un valor de 1 dadas esas condiciones de entrada.

Por ejemplo, en la cuarta fila hacia abajo en la tabla de verdad para nuestro sistema lógico dos de tres, donde A =0, B =1 y C =1, el término producto sería A'BC, ya que ese término tendría un valor de 1 si y solo si A =0, B =1 y C =1:

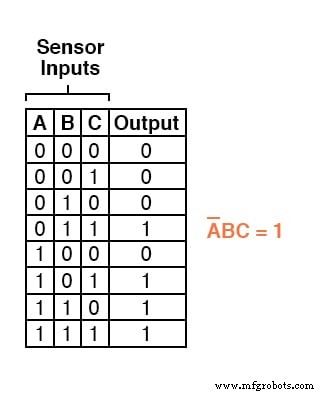
Otras tres filas de la tabla de verdad tienen un valor de salida de 1, por lo que esas filas también necesitan expresiones de producto booleanas para representarlas:

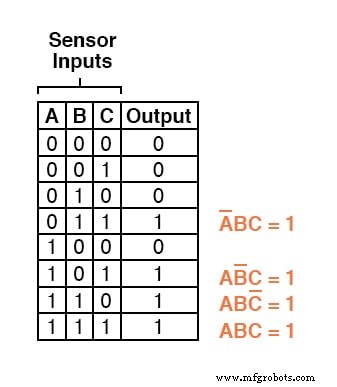
Finalmente, unimos estas cuatro expresiones de productos booleanos por suma, para crear una sola expresión booleana que describa la tabla de verdad como un todo:

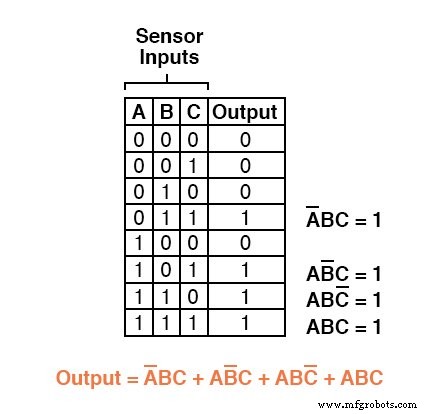
Ahora que tenemos una expresión booleana de suma de productos para la función de la tabla de verdad, podemos diseñar fácilmente una puerta lógica o un circuito lógico de relé basado en esa expresión:

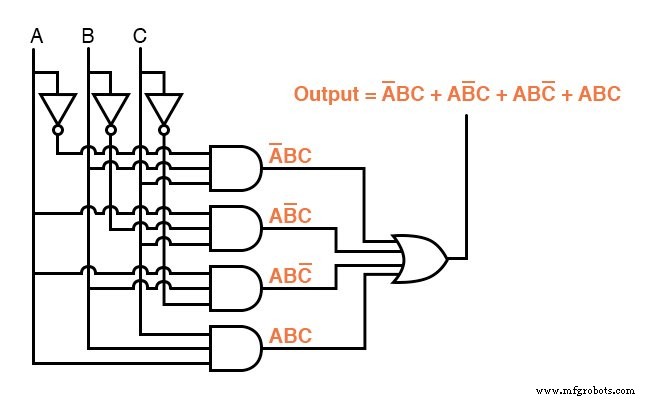
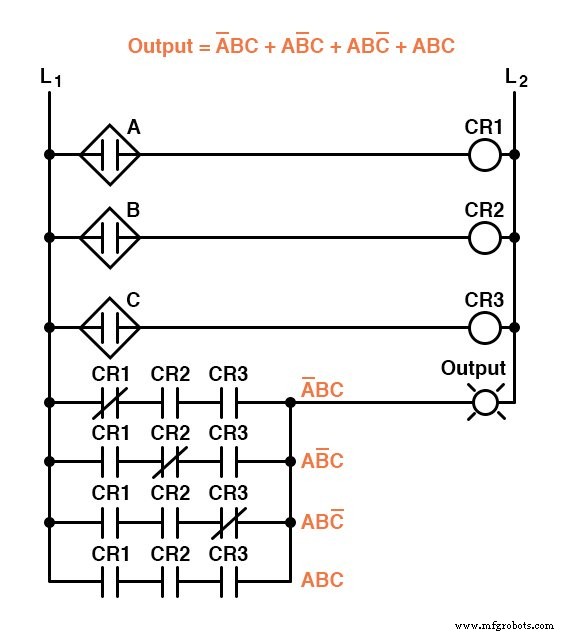
Desafortunadamente, ambos circuitos son bastante complejos y podrían beneficiarse de la simplificación.

Usando técnicas de álgebra booleana, la expresión puede simplificarse significativamente:

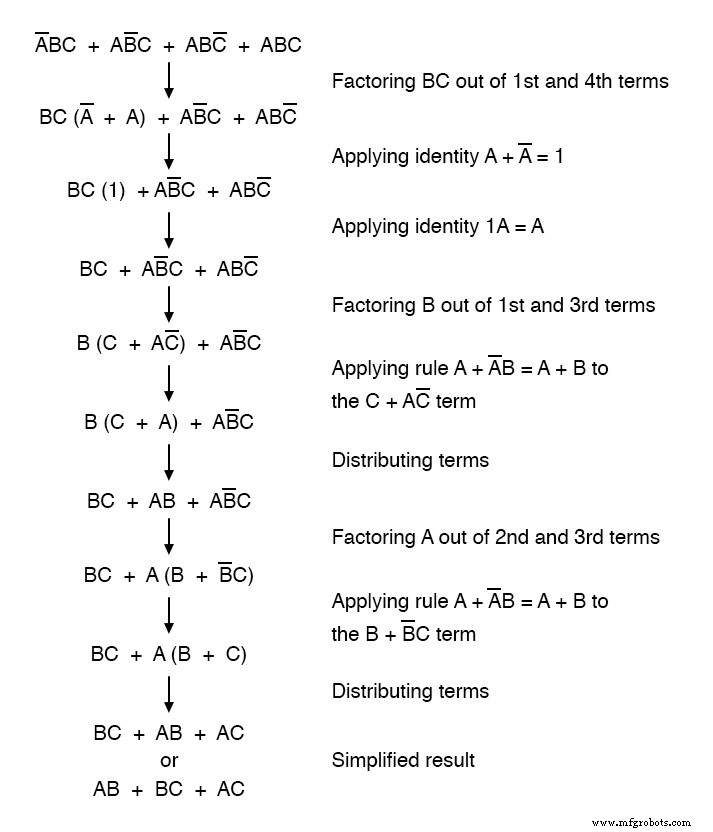
Como resultado de la simplificación, ahora podemos construir circuitos lógicos mucho más simples que realizan la misma función, ya sea en forma de puerta o relé:

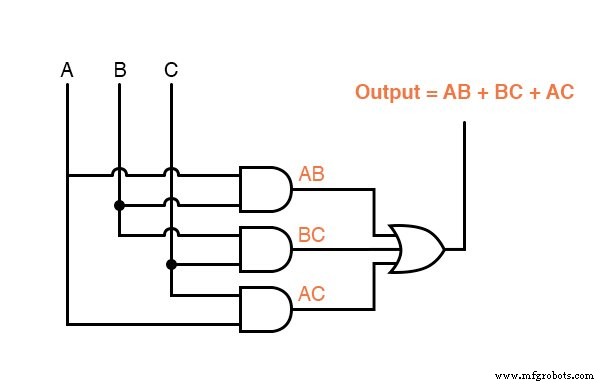
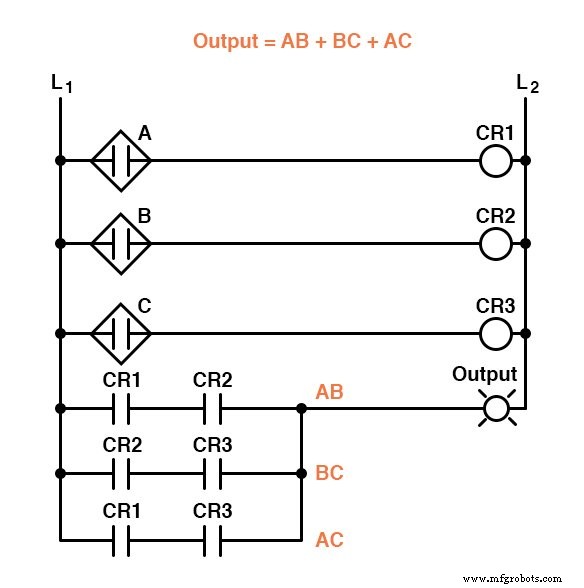
Cualquiera de estos circuitos realizará adecuadamente la tarea de operar la válvula de desechos del incinerador basándose en una verificación de llama de dos de los tres sensores de llama.

Como mínimo, esto es lo que necesitamos para tener un sistema incinerador seguro.

Sin embargo, podemos extender la funcionalidad del sistema agregando circuitos lógicos diseñados para detectar si alguno de los sensores no está de acuerdo con los otros dos.

Si los tres sensores funcionan correctamente, deberían detectar la llama con la misma precisión.

Por lo tanto, todos deberían registrar "bajo" (000:sin llama) o todos registrar "alto" (111:buena llama).

Cualquier otra combinación de salida (001, 010, 011, 100, 101 o 110) constituye un desacuerdo entre los sensores y, por lo tanto, puede servir como indicador de una falla potencial del sensor.

Si agregamos un circuito para detectar cualquiera de las seis condiciones de "desacuerdo del sensor", podríamos usar la salida de ese circuito para activar una alarma.

Quien esté monitoreando el incinerador entonces ejercerá su juicio al continuar operando con un posible sensor fallado (entradas:011, 101 o 110), o apagar el incinerador para estar absolutamente seguro.

Además, si el incinerador está apagado (sin llama), y uno o más de los sensores aún indican llama (001, 010, 011, 100, 101 o 110) mientras que los otros indican que no hay llama, se sabrá que existe un problema definido del sensor.

El primer paso para diseñar este circuito de detección de "desacuerdo del sensor" es escribir una tabla de verdad que describa su comportamiento.

Como ya tenemos una tabla de verdad que describe la salida del circuito lógico de "llama buena", podemos simplemente agregar otra columna de salida a la tabla para representar el segundo circuito y hacer una tabla que represente todo el sistema lógico:

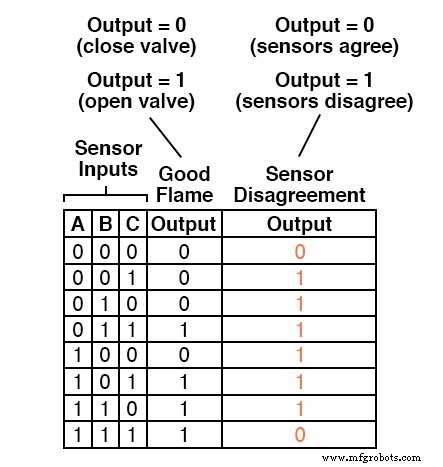
Si bien es posible generar una expresión de suma de productos para esta nueva columna de la tabla de verdad, se necesitarían seis términos, de tres variables cada uno.

Una expresión booleana de este tipo requeriría muchos pasos para simplificarse, con un gran potencial para cometer errores algebraicos:

Uso de producto de sumas

Una alternativa a generar una expresión de suma de productos para tener en cuenta todas las condiciones de salida "altas" (1) en la tabla de verdad es generar un producto de sumas o POS , expresión, para tener en cuenta todas las condiciones de salida "bajas" (0) en su lugar.

Dado que hay muchas menos instancias de una salida "baja" en la última columna de la tabla de verdad, la expresión Producto-de-Sumas resultante debe contener menos términos.

Como sugiere su nombre, una expresión de producto de sumas es un conjunto de términos agregados ( sumas ), que se multiplican ( producto ) juntos.

Un ejemplo de expresión POS sería (A + B) (C + D), el producto de las sumas "A + B" y "C + D".

Para comenzar, identificamos qué filas en la última columna de la tabla de verdad tienen salidas "bajas" (0) y escribimos un término de suma booleana que sería igual a 0 para las condiciones de entrada de esa fila.

Por ejemplo, en la primera fila de la tabla de verdad, donde A =0, B =0 y C =0, el término suma sería (A + B + C), ya que ese término tendría un valor de 0 si y solo si A =0, B =0 y C =0:

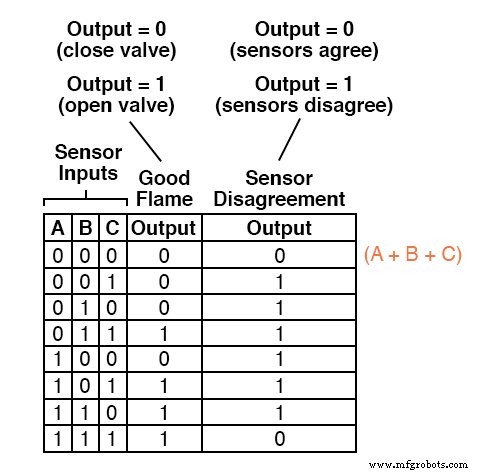
Solo otra fila en la última columna de la tabla de verdad tiene una salida "baja" (0), por lo que todo lo que necesitamos es un término de suma más para completar nuestra expresión Producto de sumas.

Este último término de suma representa una salida 0 para una condición de entrada de A =1, B =1 y C =1.

Por lo tanto, el término debe escribirse como (A ’+ B’ + C ’), porque solo la suma de los complementados las variables de entrada serían iguales a 0 solo para esa condición:

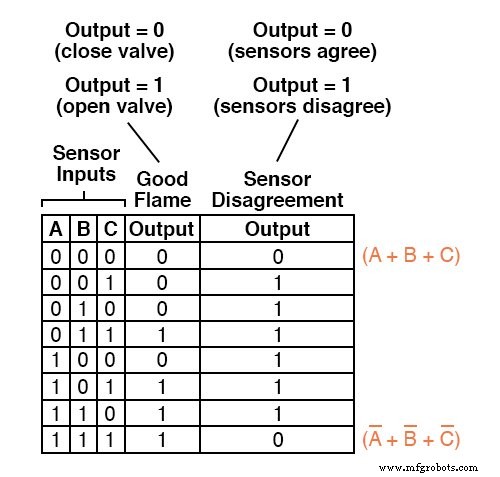
La expresión Producto-de-Sumas completa, por supuesto, es la combinación multiplicativa de estos dos términos de suma:

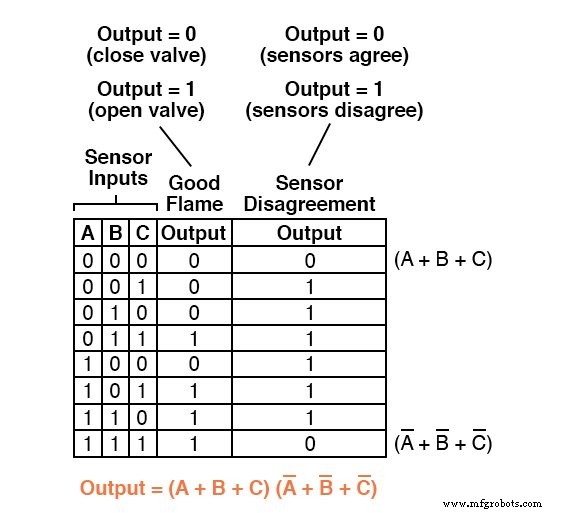
Mientras que una expresión de suma de productos podría implementarse en forma de un conjunto de puertas AND con sus salidas conectadas a una única puerta OR, una expresión de producto de sumas se puede implementar como un conjunto de puertas OR que se alimentan en una única puerta. Y puerta:

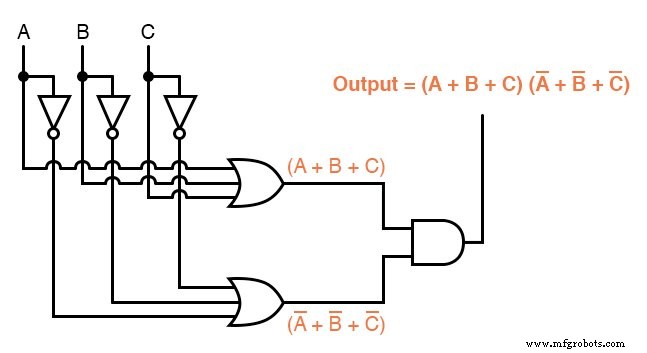
En consecuencia, mientras que una expresión de suma de productos podría implementarse como una colección en paralelo de contactos de relé conectados en serie, una expresión de producto de sumas se puede implementar como una colección en serie de contactos de relé conectados en paralelo:

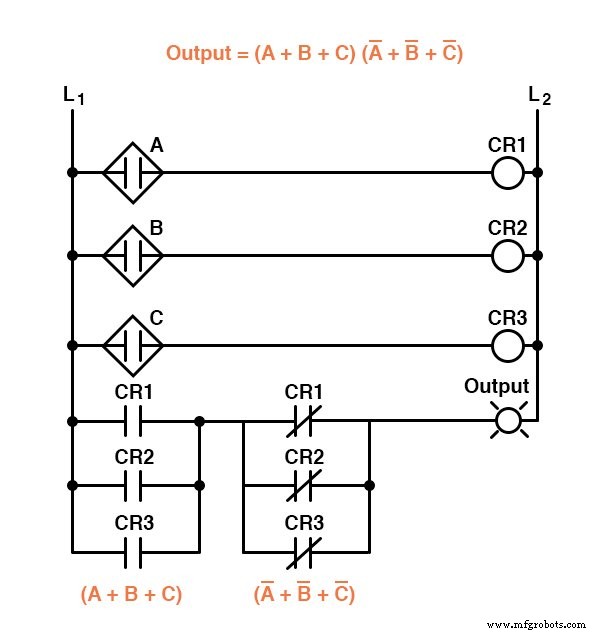
Los dos circuitos anteriores representan versiones diferentes del circuito lógico de "desacuerdo del sensor" únicamente, no el circuito o circuitos de detección de "llama buena".

Todo el sistema lógico sería la combinación de los circuitos de "llama buena" y "desacuerdo del sensor", que se muestran en el mismo diagrama.

Implementado en un controlador lógico programable (PLC), todo el sistema lógico podría parecerse a algo como esto:

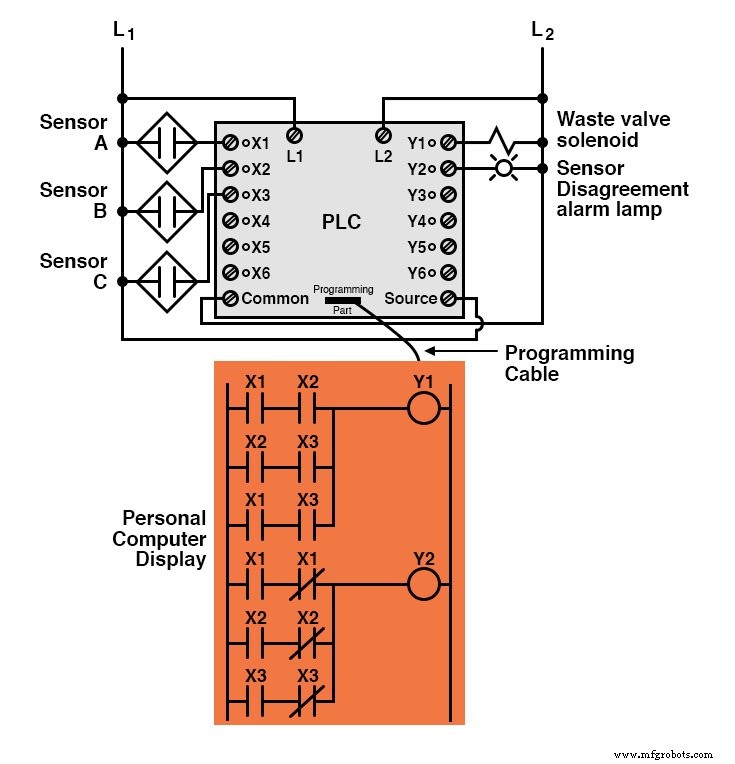
Como puede ver, las formas booleanas estándar Suma de productos y Productos de sumas son herramientas poderosas cuando se aplican a tablas de verdad.

Nos permiten derivar una expresión booleana y, en última instancia, un circuito lógico real, de nada más que una tabla de verdad, que es una especificación escrita de lo que queremos que haga un circuito lógico.

Poder pasar de una especificación escrita a un circuito real utilizando procedimientos deterministas simples significa que es posible automatizar el proceso de diseño de un circuito digital.

En otras palabras, una computadora podría programarse para diseñar un circuito lógico personalizado a partir de una especificación de tabla de verdad.

Los pasos a seguir desde una tabla de verdad hasta el circuito final son tan inequívocos y directos que se requiere poca o ninguna creatividad u otro pensamiento original para ejecutarlos.

REVISAR:

• Suma de productos o SOP Las expresiones booleanas se pueden generar a partir de tablas de verdad con bastante facilidad, determinando qué filas de la tabla tienen una salida de 1, escribiendo un término de producto para cada fila y finalmente sumando todos los términos de producto. Esto crea una expresión booleana que representa la tabla de verdad como un todo.
• Las expresiones de suma de productos se prestan bien a la implementación como un conjunto de puertas AND (productos) que se alimentan de una única puerta OR (suma).
• Producto de las sumas o POS Las expresiones booleanas también se pueden generar a partir de tablas de verdad con bastante facilidad, determinando qué filas de la tabla tienen una salida de 0, escribiendo un término de suma para cada fila y finalmente multiplicando todos los términos de suma. Esto crea una expresión booleana que representa la tabla de verdad como un todo.
• Las expresiones de producto de sumas se prestan bien a la implementación como un conjunto de puertas OR (sumas) que ingresan a una única puerta AND (producto).

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de expresiones de suma de productos y producto de sumas
• Hoja de trabajo de álgebra booleana