Resolver ecuaciones simultáneas:el método de sustitución y el método de suma

¿Qué son las ecuaciones y los sistemas de ecuaciones simultáneos?

Los términos ecuaciones simultáneas y sistemas de ecuaciones se refieren a condiciones en las que dos o más variables desconocidas están relacionadas entre sí a través de un número igual de ecuaciones.

Ejemplo:

Para este conjunto de ecuaciones, existe una única combinación de valores para x y y que satisfará a ambos.

Cualquiera de las ecuaciones, considerada por separado, tiene una infinitud de (x, y) válidas. soluciones, pero juntos sólo hay uno. Trazada en un gráfico, esta condición se vuelve obvia:

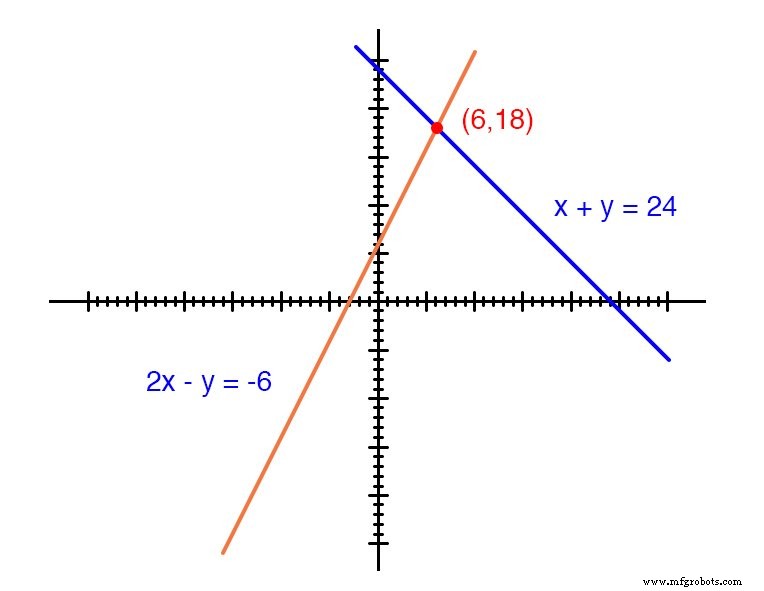
Cada línea es en realidad un continuo de puntos que representan posibles x y y pares de soluciones para cada ecuación.

Cada ecuación, por separado, tiene un número infinito de pares ordenados ( x , y ) soluciones. Solo hay un punto donde las dos funciones lineales x + y =24 y 2x - y =-6 se intersecan (donde una de sus muchas soluciones independientes funciona para ambas ecuaciones), y ahí es donde x es igual a un valor de 6 y y es igual a un valor de 18.

Sin embargo, por lo general, la representación gráfica no es una forma muy eficiente de determinar el conjunto de soluciones simultáneas para dos o más ecuaciones. Es especialmente impráctico para sistemas de tres o más variables.

En un sistema de tres variables, por ejemplo, la solución se encontraría mediante la intersección de tres planos en un espacio de coordenadas tridimensionales, lo que no es un escenario fácil de visualizar.

Resolver ecuaciones simultáneas mediante el método de sustitución

Existen varias técnicas algebraicas para resolver ecuaciones simultáneas.

Quizás el más fácil de comprender es la sustitución método.

Tomemos, por ejemplo, nuestro problema de ejemplo de dos variables:

En el método de sustitución, manipulamos una de las ecuaciones de modo que una variable se defina en términos de la otra:

Luego, tomamos esta nueva definición de una variable y sustituto para la misma variable en la otra ecuación.

En este caso, tomamos la definición de y , que es 24 - x y sustituya esto por y término encontrado en la otra ecuación:

Ahora que tenemos una ecuación con una sola variable ( x ), podemos resolverlo usando técnicas algebraicas "normales":

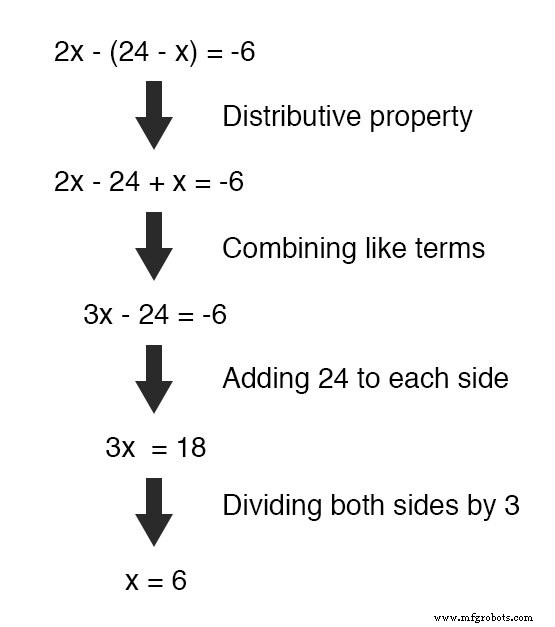
Ahora que x se conoce, podemos insertar este valor en cualquiera de las ecuaciones originales y obtener un valor para y.

O, para ahorrarnos algo de trabajo, podemos insertar este valor (6) en la ecuación que acabamos de generar para definir y en términos de x , siendo que ya está en forma de resolver para y :

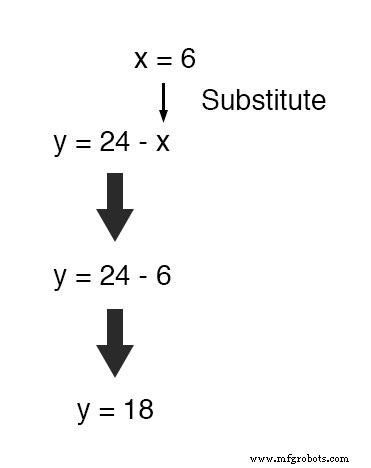
Aplicar el método de sustitución a sistemas de tres o más variables implica un patrón similar, solo que con más trabajo involucrado.

Esto es generalmente cierto para cualquier método de solución:el número de pasos necesarios para obtener soluciones aumenta rápidamente con cada variable adicional en el sistema.

Para resolver tres variables desconocidas, necesitamos al menos tres ecuaciones. Considere este ejemplo:

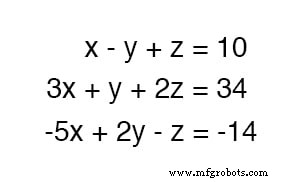
Siendo que la primera ecuación tiene los coeficientes más simples (1, -1 y 1, para x , y y z , respectivamente), parece lógico utilizarlo para desarrollar una definición de una variable en términos de las otras dos.

Resuelve para x en términos de y y z :

Ahora, podemos sustituir esta definición de x donde x aparece en las otras dos ecuaciones:

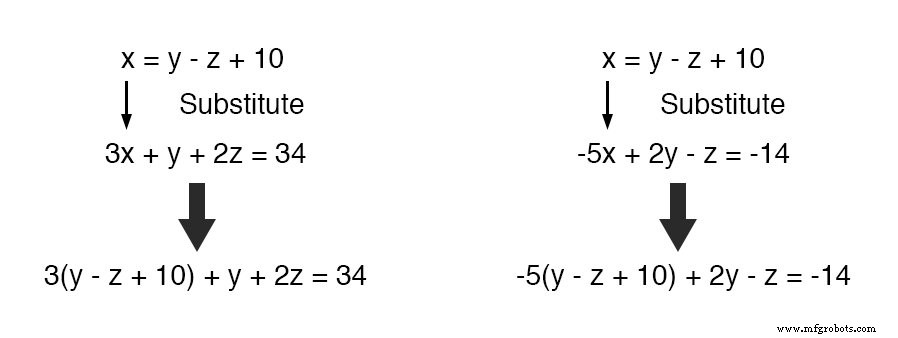
Reduciendo estas dos ecuaciones a sus formas más simples:

Hasta ahora, nuestros esfuerzos han reducido el sistema de tres variables en tres ecuaciones a dos variables en dos ecuaciones.

Ahora, podemos aplicar la técnica de sustitución nuevamente a las dos ecuaciones 4y - z =4 y -3y + 4z =36 para resolver para y o z . Primero, manipularé la primera ecuación para definir z en términos de y :

A continuación, sustituiremos esta definición de z en términos de y donde vemos z en la otra ecuación:

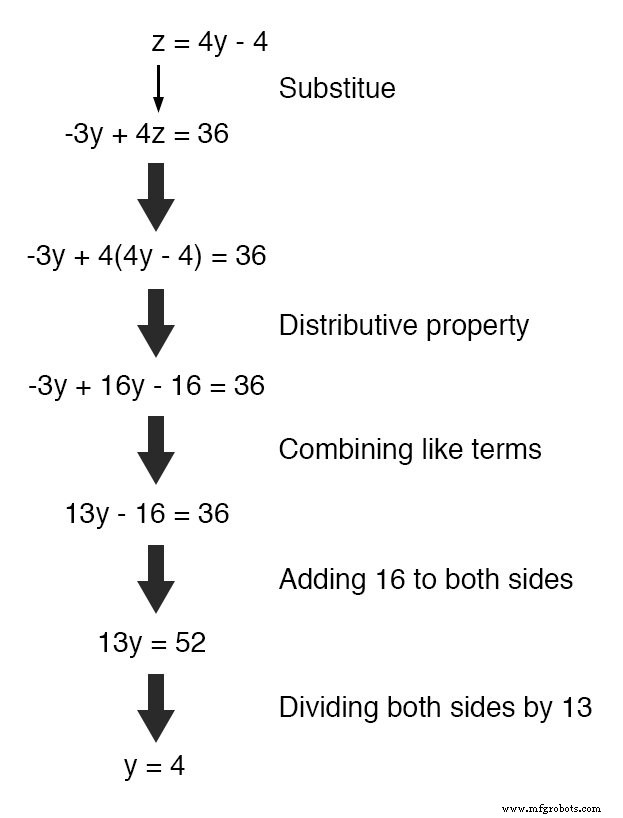
Ahora que y es un valor conocido, podemos insertarlo en la ecuación que define z en términos de y y obtenga una cifra para z :

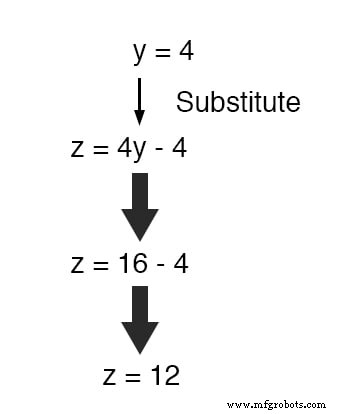
Ahora, con valores para y y z conocidos, podemos insertarlos en la ecuación donde definimos x en términos de y y z , para obtener un valor para x :

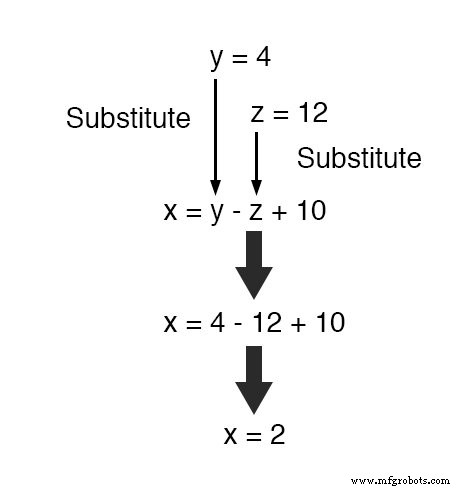
Para terminar, hemos encontrado valores para x , y y z de 2, 4 y 12, respectivamente, que satisfacen las tres ecuaciones.

Resolver ecuaciones simultáneas mediante el método de suma

Si bien el método de sustitución puede ser el más fácil de comprender a nivel conceptual, existen otros métodos de solución disponibles para nosotros.

Uno de esos métodos es la llamada adición método, mediante el cual las ecuaciones se agregan entre sí con el propósito de cancelar términos variables.

Tomemos nuestro sistema de dos variables utilizado para demostrar el método de sustitución:

Una de las reglas del álgebra más utilizadas es que puedes realizar cualquier operación aritmética que desees con una ecuación siempre que la hagas por igual en ambos lados .

Con referencia a la suma, esto significa que podemos agregar cualquier cantidad que queramos a ambos lados de una ecuación, siempre que sea igual cantidad, sin alterar la verdad de la ecuación.

Una opción que tenemos, entonces, es sumar los lados correspondientes de las ecuaciones para formar una nueva ecuación.

Dado que cada ecuación es una expresión de igualdad (la misma cantidad a cada lado del = signo), sumar el lado izquierdo de una ecuación al lado izquierdo de la otra ecuación es válido siempre que sumemos los lados derechos de las dos ecuaciones también.

En nuestro conjunto de ecuaciones de ejemplo, por ejemplo, podemos agregar x + y a 2x - y y agregue 24 y -6 juntos también para formar una nueva ecuación.

¿Qué beneficio tiene esto para nosotros? Examine lo que sucede cuando hacemos esto con nuestro conjunto de ecuaciones de ejemplo:

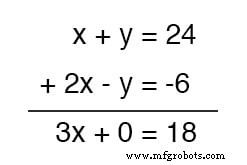
Debido a que la ecuación superior pasó a contener una y positiva término mientras que la ecuación inferior contenía un y negativo término, estos dos términos se cancelaron entre sí en el proceso de adición, sin dejar y término en la suma.

Lo que nos queda es una nueva ecuación, pero una con una sola variable desconocida, x ! Esto nos permite resolver fácilmente el valor de x :

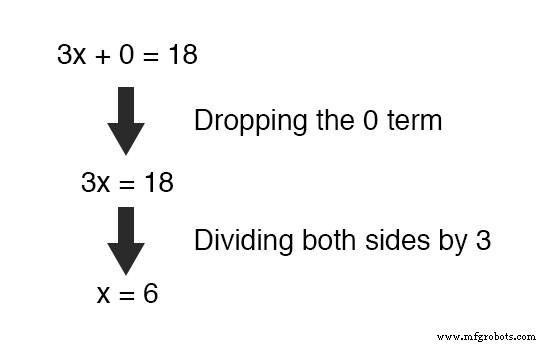
Una vez que tengamos un valor conocido para x , por supuesto, determinando y El valor es simplemente una cuestión de sustitución (reemplazando x con el número 6 ) en una de las ecuaciones originales.

En este ejemplo, la técnica de sumar las ecuaciones funcionó bien para producir una ecuación con una sola variable desconocida.

¿Qué tal un ejemplo en el que las cosas no son tan simples? Considere el siguiente conjunto de ecuaciones:

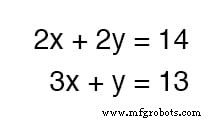
Podríamos sumar estas dos ecuaciones, siendo esta una operación algebraica completamente válida, pero no nos beneficiaría en el objetivo de obtener valores para x y y :

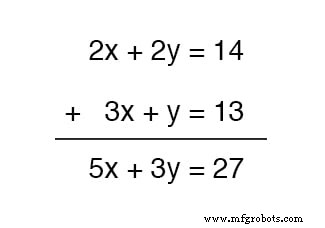
La ecuación resultante todavía contiene dos variables desconocidas, al igual que las ecuaciones originales, por lo que no estamos más avanzados en la obtención de una solución.

Sin embargo, ¿qué pasaría si pudiéramos manipular una de las ecuaciones para tener un término negativo que haría cancelar el término respectivo en la otra ecuación cuando se agrega?

Entonces, el sistema se reduciría a una sola ecuación con una sola variable desconocida al igual que con el último ejemplo (fortuito).

Si tan solo pudiéramos convertir el y término en la ecuación inferior en un - 2y término, de modo que cuando se suman las dos ecuaciones, ambas y términos en las ecuaciones se cancelarían, dejándonos con solo una x plazo, esto nos acercaría a una solución.

Afortunadamente, esto no es difícil de hacer. Si multiplicamos todos y cada uno de los términos de la ecuación inferior por un -2 , producirá el resultado que buscamos:

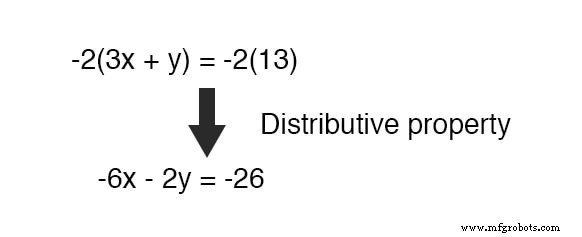
Ahora, podemos agregar esta nueva ecuación a la ecuación superior original:

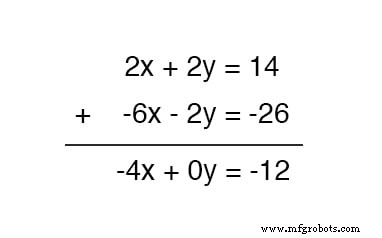
Resolviendo para x , obtenemos un valor de 3 :

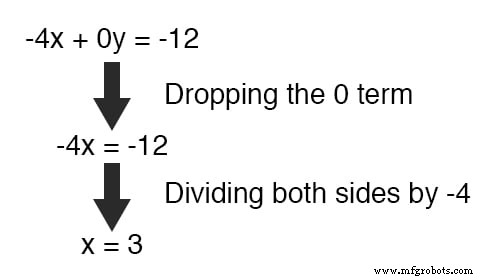
Sustituyendo este nuevo valor encontrado por x en una de las ecuaciones originales, el valor de y se determina fácilmente:

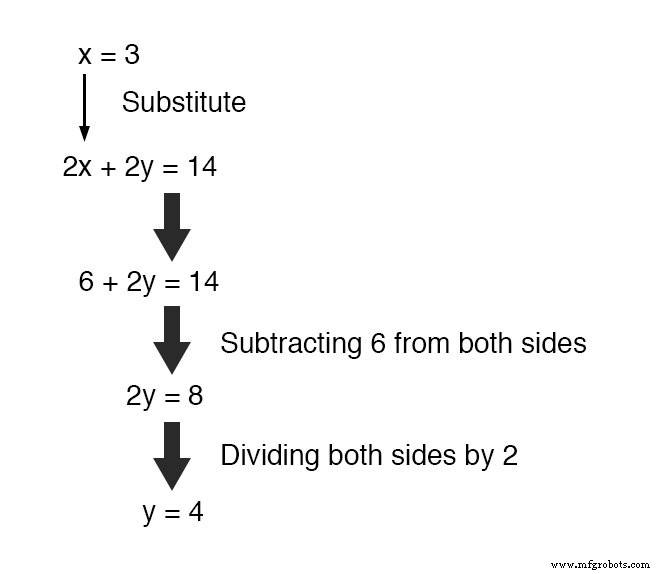
Usar esta técnica de solución en un sistema de tres variables es un poco más complejo.

Al igual que con la sustitución, debe usar esta técnica para reducir el sistema de tres ecuaciones de tres variables a dos ecuaciones con dos variables, luego aplicarla nuevamente para obtener una sola ecuación con una variable desconocida.

Para demostrarlo, usaré el sistema de ecuaciones de tres variables de la sección de sustitución:

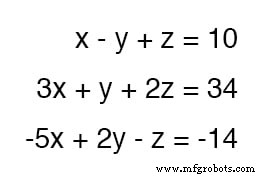
Siendo que la ecuación superior tiene valores de coeficiente de 1 para cada variable, será una ecuación fácil de manipular y usar como herramienta de cancelación.

Por ejemplo, si deseamos cancelar el 3x término de la ecuación del medio, todo lo que tenemos que hacer es tomar la ecuación superior, multiplicar cada uno de sus términos por -3 , luego agréguelo a la ecuación del medio de esta manera:

Podemos eliminar la ecuación inferior de su -5x término de la misma manera:tome la ecuación superior original, multiplique cada uno de sus términos por 5 , luego agregue esa ecuación modificada a la ecuación inferior, dejando una nueva ecuación con solo y y z términos:

En este punto, tenemos dos ecuaciones con las mismas dos variables desconocidas, y y z :

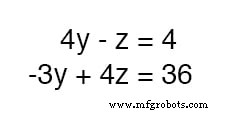
Por inspección, debería ser evidente que el -z El término de la ecuación superior podría aprovecharse para cancelar el 4z término en la ecuación inferior si solo multiplicamos cada término de la ecuación superior por 4 y sume las dos ecuaciones:

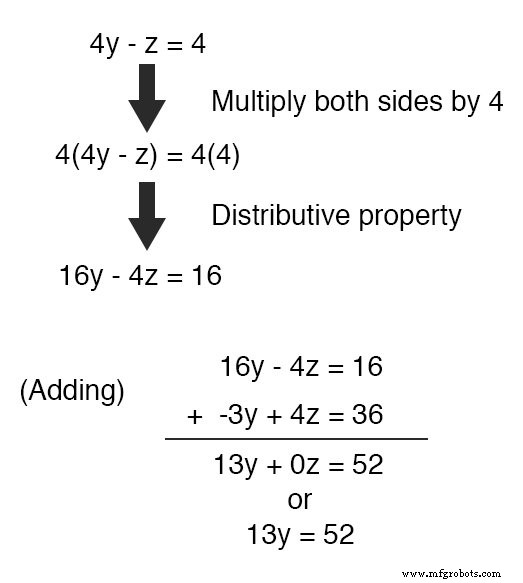
Tomando la nueva ecuación 13y =52 y resolviendo para y (dividiendo ambos lados por 13 ), obtenemos un valor de 4 por y .

Sustituyendo este valor de 4 por y en cualquiera de las ecuaciones de dos variables nos permite resolver para z .

Sustituyendo ambos valores de y y z en cualquiera de las ecuaciones originales de tres variables nos permite resolver para x .

El resultado final (¡te ahorraré los pasos algebraicos ya que ya deberías estar familiarizado con ellos!) Es que x =2 , y =4 y z =12 .

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de ecuaciones simultáneas para análisis de circuitos