Fórmulas matemáticas mágicas para nanocajas

Dado que creamos matrices de adyacencia vecinas más cercanas, conocemos el número de coordinación \ (\ hbox {cn} _i \) del vértice i sumando los elementos de \ ({{\ mathbf {A}}} (i,:) \). Nuestra estructura consta de \ (n + 1 \) conchas numeradas 0, 1, ..., n , con t capas exteriores. Sea \ (N _ {{\ rm cn} _i} (n, t) \) el número de átomos con coordinación \ (\ hbox {cn} _i \) donde \ (1 \ le \ hbox {cn} _i \ le \ hbox {cn} _M \) con \ (\ hbox {cn} _M \) la máxima coordinación en el nanobox. Entonces, el número total de átomos en la nanocaja viene dado por

Los átomos de la superficie en la capa exterior (o interior) de la nanocaja, n tienen un conjunto de enlaces menor que la coordinación a granel. Por tanto, la coordinación máxima para los átomos de la superficie es \ (\ hbox {cn} _s <\ hbox {cn} _M \), y el número de átomos de la superficie es

Esto es válido si todos los vértices que no son de superficie tienen una coordinación mayor que \ (\ hbox {cn} _s \), lo cual es cierto para todos los clústeres fcc, bcc y hcp. Determinamos \ (N _ {{\ rm cn} _i} (n, t) \) contando las columnas de la matriz de adyacencia cuya suma es \ (\ hbox {cn} _i \). Tenga en cuenta que nuestro algoritmo de coordenadas de clúster está construido por shells, por lo que cada shell subsiguiente contiene todos los valores inferiores anteriores de n . Además, el número de enlaces en el cuadro es

donde \ (N _ {{\ rm B}} (n, t) \) es el número de enlaces y \ (\ hbox {cn} _M \) es la máxima coordinación. El factor de 1/2 se produce debido a la vinculación del vecino más cercano por pares.

Como sabemos que estas ecuaciones dependen de n , t como un polinomio de grado 3 como máximo, podemos calcular \ (N _ {{\ rm cn} _i} (n, t) \) para 4 valores consecutivos de n , digamos \ (n =n_0 + j \), j =0, 1, 2, 3. Un polinomio de interpolación simple dará entonces los coeficientes del polinomio. Hay que comprobar que aumentando \ (n_0 \), que suele ser igual a 1, las fórmulas no cambian. Si las fórmulas se estabilizan desde \ (n_0 \) en adelante, entonces se mantienen para todos \ (n \ ge n_0 \). Para obtener los coeficientes racionales exactos, es necesario resolver el sistema de Vandermonde para los coeficientes en aritmética exacta.

Tenga en cuenta que en las fórmulas mágicas para nanocajas tenemos que \ (n> t \) de modo que, por lo tanto, contrariamente a cualquier expectativa, llene la caja con una elección adecuada de t no volverá a crear las fórmulas mágicas originales para los grupos sólidos completos. Estas fórmulas mágicas son útiles para modelar las propiedades de mesoescala de grupos y cajas o jaulas. Los conjuntos completos de fórmulas se derivaron originalmente para diecinueve tipos de conglomerados. En este manuscrito, obtenemos fórmulas mágicas para trece tipos de nanocajas.

En las fórmulas mágicas a continuación, encontramos que la coordinación masiva puede aparecer para t =2 o t =3 capas de espesor de caparazón. La mayoría son para capas donde t =2; las excepciones son el cubo fcc, el cuboctaedro, el icosaedro y el cubo bcc y el cubo truncado. En este último, la coordinación masiva solo aparece para t =3 capas. Para los datos a continuación, las tablas de las fórmulas mágicas van acompañadas de una figura de una "media caja" para mostrar el interior de las nanocajas. Al lado hay una barra de colores que indica la coordinación y el número de los mismos entre paréntesis.

Resultados y discusión

Para delinear la aplicabilidad de las fórmulas mágicas, describimos cómo el comportamiento catalítico puede depender de la coordinación y tales fórmulas. Definimos G como la energía de Gibbs dependiente del tamaño del cúmulo. Debido a que los adatomos están unidos a los átomos de la capa exterior, hay un aumento en G eso se llama energía de adsorción y se denota como \ (\ Delta G \). Esto se puede dividir en diferentes tipos de coordinación de los átomos de la capa exterior que se unen a los adatomos. Por ejemplo, un átomo retorcido se suma a la energía de adsorción con una cantidad \ (\ Delta G_ {k} \). De manera similar, un átomo de borde agrega \ (\ Delta G_ {e} \), mientras que un átomo de faceta contribuye \ (\ Delta G_f \) luego [18]:

$$ \ Delta G =\ sum _ {o \ in \ {f, e, k \}} \ Delta G_o N_o $$ (7)

donde \ (N_o \) es el número de átomos en la capa exterior del tipo indicado. El número total de átomos en la capa exterior unidos a adatoms se define como \ (N_s =N_f + N_e + N_k \), lo que da como resultado:

$$ \ begin {alineado} \ Delta G =&{} \ Delta G_f \ cdot (1-f_e-f_k) + \ Delta G_e \ cdot f_e + \ Delta G_k \ cdot f_k \\ &\ quad {\ hbox {donde} } \, \, f_o =N_o / N_s, \, \, o \ in \ {e, k \}, \ end {alineado} $$ (8)

con la fracción de energía de Gibbs expresada a través de los sitios de borde y torsión que tienen coordinaciones explícitas para estructuras específicas. Esto demuestra que las fórmulas mágicas tienen un papel en las reacciones superficiales, a través de las coordinaciones de bordes y torceduras y sus fórmulas. Tenga en cuenta que la ecuación. (8) se aplica a la adsorción en sitios superiores; de lo contrario, no todos los adatomos se unirán a los átomos de la capa exterior. En tal modelo, los sitios de torceduras tienen fórmulas mágicas que son constantes con el número de conchas, n , los sitios de borde tienen fórmulas que son lineales con n y los sitios de facetas tienen fórmulas cuadráticas con n . Más específicamente, los sitios de torcedura son las fórmulas coordinadas más bajas, los sitios de borde son los segundos coordinados más bajos y los sitios de facetas tienen cn =8 para (100) facetas y cn =9 para (111) facetas.

Se pueden aplicar dos relaciones fundamentales por partícula. Para la constante de adsorción y energía de Gibbs, \ (K _ {{\ rm a}} \), se mantiene:

$$ K _ {{\ rm a}} ={\ exp} \ left (- \ frac {\ Delta G} {RT} \ right), $$ (9)

donde R es la constante de gas y T es la temperatura en grados Kelvin. Además, las relaciones de Brønsted-Evans-Polanyi se utilizan ampliamente en catálisis homogénea y heterogénea [18, 22] utilizando una relación para las constantes de reacción k y constantes de equilibrio K de la siguiente manera:

$$ k =gK ^ {\ alpha}, \ quad 0 <\ alpha <1, $$ (10)

donde g y \ (\ alpha \) (parámetro de Polanyi) son constantes. El parámetro de Polanyi no tiene unidades y es una fracción propia, como lo dio originalmente Brønsted [23]. Entonces tenemos:

$$ k =k '_ {a} {\ exp} \ Bigl (- \ alpha \ bigl ({f_n ^ {e} \ cdot \ chi _ {_ e} ({D_n}) + f_n ^ {k} \ cdot \ chi _ {_ k} ({D_n})} \ bigr) \ Bigr), $$ (11)

donde

$$ \ begin {alineado} &\ chi _ {_ e} (D) =\ frac {\ Delta G_e (D) - \ Delta G_f (D)} {RT}, \\ &\ chi _ {_ k} (D ) =\ frac {\ Delta G_k (D) - \ Delta G_f (D)} {RT}, \ end {alineado} $$ (12)

y

$$ k '_ {a} =g \ exp \ left (- \ alpha \ frac {\ Delta G_f} {RT} \ right). $$ (13)

Este análisis muestra que la determinación de un modelo catalítico requiere un método para calcular la energía de Gibbs. Se han considerado reacciones catalíticas conocidas como los mecanismos de dos pasos y Langmuir-Hinshelwood [24].

Nanoboxes de la FCC

Las estructuras cúbicas centradas en la cara son la forma más común de nanoclusters y nanoboxes. Esta es la estructura de los metales con propiedades interesantes, como los metales nobles con propiedades plasmónicas y los metales preciosos catalíticos. Dado que el oro tiene un alto potencial de reducción de 1,50 V (ver Ec. 1) en comparación con el electrodo de hidrógeno estándar (SHE) [5], es uno de los metales más fáciles de sintetizar como nanocaja o nanocaja. Se han formado nanocajas o nanocajas de oro en formas cúbica [1], cuboctaedro [25], icosaedro y decaedro [26], octaedro [27] y tetraedro [28].

Podemos determinar el tamaño aproximado de estas nanocajas usando un enfoque de coordinación para la longitud de enlace del vecino más cercano r (cn) [29],

$$ r (cn) =\ frac {2r _ {{\ rm B}}} {\ left (1+ \ exp \ left (\ frac {12 - \ langle cn \ rangle _c)} {8 \ cdot \ langle cn \ rangle _c} \ right) \ right)}. $$ (14)

Aquí \ (r _ {{\ rm B}} \) es la longitud del enlace masivo para el oro (0.2884 nm) y \ (\ langle cn \ rangle _c \) es la coordinación promedio del grupo. Encontramos una relación lineal entre D y n , el número de conchas de clúster, como se muestra en la Tabla 1:

$$ D (n) =a \ cdot r _ {{\ rm B}} \ cdot n + b. $$ (15)

Usamos nanocajas con t =3, ya que las fórmulas varían con t , y deseamos lograr cierta coordinación masiva. Para el cálculo de D ( n ), usamos la distancia máxima entre átomos en el cúmulo, derivada de la matriz euclidiana. Tenga en cuenta que D ( n ) es una fórmula empírica, derivada de datos (varían n y calcular D ), y como tal no está probado.

Estas relaciones producen diámetros de acuerdo con otros datos, de DFT. Para el cuboctaedro sólido con N igual a 55, 561 y 923 obtenemos diámetros de 1,12 nm, 2,85 nm y 3,43 nm. Esto se compara favorablemente con los resultados publicados de DFT para 55 átomos de 1,1 nm [30], para 561 átomos, 2,7 nm [31] y para 923 átomos, 3,5 nm [30]. Las fórmulas mágicas para algunas nanocajas de fcc se tabulan a continuación (Tablas 2, 3, 4, 5, 6, 7, 8).

Nanocajas icosaédricas y decaédricas

Consulte las tablas 9 y 10.

Nanocajas cúbicas simples y de diamante

La estructura de celosía cúbica del diamante está formada por un alótropo de carbono y los elementos silicio y germanio. Además, algunos compuestos cúbicos forman esta estructura, como óxido de hierro cúbico, maghemita de diamante tetraédrico \ (\ gamma \) - Fe ₂ O ₃ . La longitud del enlace para Fe – O en la maghemita \ (\ gamma \) - Fe ₂ de diamante tetraédrico O ₃ =0,186 nm [32]. Esto conduce al diámetro de los grupos de diamantes D ( n ) como se muestra a continuación:

$$ D (n) =3.3984 \ cdot n _ {{\ rm B}} \ cdot n - 0.21194. $$ (16)

Según la referencia [12], se formaron microcajas de óxido de hierro cúbico que tenían interesantes capacidades de almacenamiento de litio. No conocemos un modelo de coordinación completo para el almacenamiento de energía, pero como se mencionó anteriormente, los resultados de DFT indican que la actividad puede depender de la orientación de las facetas [19]. Actualmente no existe tal modelo de dependencia del almacenamiento en la coordinación como el que tenemos para la catálisis. De la ecuación (16) anterior (creada con t =4), una microcaja requiere aproximadamente n =1600 conchas de diamante maghemita. Las fórmulas mágicas para el diamante y las estructuras de celosía cúbica simple se enumeran a continuación (Tablas 11, 12).

Nanoboxes CCO

Consulte las tablas 13, 14 y 15.

Nanocajas de HCP

Consulte la Tabla 16.

El caso t =1

El caso especial t =1 es único y, como tal, tiene distintas fórmulas mágicas. Examinamos este caso para algunas de las nanocajas anteriores. Se han formado nanocajas con paredes ultrafinas con formas cúbica [33], octaédrica [16] e icosaédrica [34]. De acuerdo con las fórmulas mágicas a continuación, la nanocaja cúbica con t =1 tiene la coordinación más baja. El platino tiene un potencial de reducción relativamente alto de 1,18 V en comparación con el SHE, por lo que puede formarse mediante sustitución galvánica, consulte la Ec. (15]. Sin embargo, las propiedades de la reacción de oxidación y reducción (ORR) de algunas de estas nanocajas a base de platino indican que las estructuras con (111) facetas en lugar de (100) facetas tienen mejores actividades de masa de ORR [35].

Así, el icosaedro con 20 (111) facetas tiene la mejor actividad de masa de ORR, seguido del octaedro y, por último, el cubo truncado. Esta propiedad del comportamiento catalítico de la orientación de facetas que tiene prioridad sobre el número de coordinación se evidencia en los datos tabulares a continuación. En otras palabras, como se menciona en las siguientes tablas, el cubo con (100) facetas tiene los números de coordinación mágica más bajos con cuatro y cinco, sin embargo, el octaedro y el icosaedro con (111) facetas y fórmulas mágicas más grandes tienen una mejor actividad de ORR. Esta propiedad también se evidencia en los nanoclusters, donde los resultados de DFT confirman el predominio de las facetas (111) [36], especialmente para las aleaciones de PtNi (Tablas 17, 18, 19, 20, 21).

Dispersión

Dada la importancia de los sitios de bordes y pliegues en relación con los de las facetas con respecto a la actividad catalítica, hemos determinado la dispersión superficial para algunas de las nanocajas que estudiamos. Las facetas (100) tienen cn =8 mientras que las facetas (111) tienen cn =9. Esto puede proporcionar información sobre las razones de la actividad poliédrica individual cuando se compara entre las nanocajas. En la Fig. 1 a continuación, graficamos la dispersión de la superficie \ (D _ {{\ rm s}} =(N _ {{\ rm e}} + N _ {{\ rm k}}) / N _ {{\ rm S}} \ cdot 100 \% \). En esta relación \ (N _ {{\ rm k}} \) es el número de sitios torcidos o de esquina y \ (N _ {{\ rm e}} \) el número de sitios de borde. Como se puede ver en la Figura 1, las nanocajas con (111) superficies en oposición a (100) superficies tienen una mayor dispersión, lo que da crédito a la preferencia de la actividad catalítica de la faceta (111).

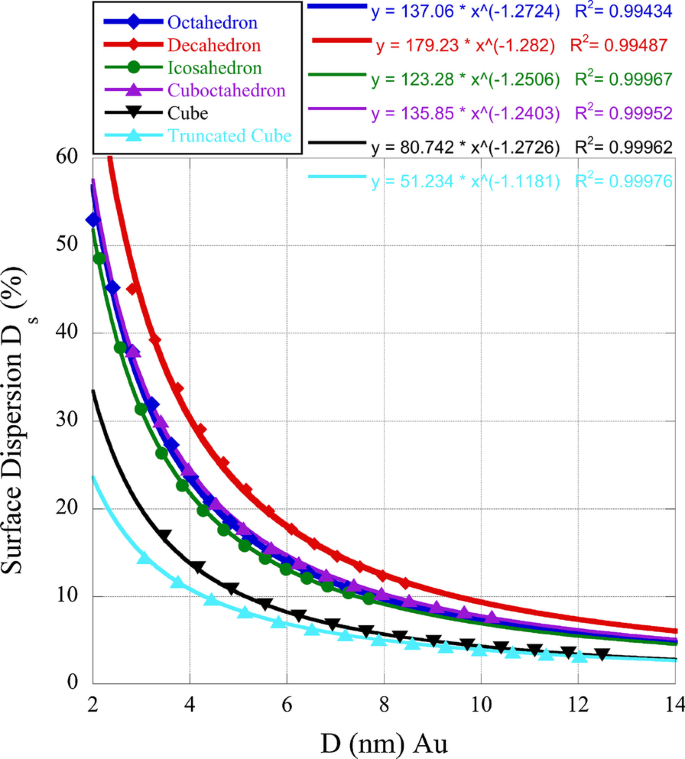
Dispersión superficial de nanocajas de oro

Conclusión

En resumen, hemos presentado la primera descripción matemática detallada de fórmulas mágicas para nanocajas. El caso del grosor de la cáscara, t =1 es distinto de \ (t> 1 \) y tabulamos los datos para algunos de estos casos. Se enumeran todas las fórmulas para la coordinación, el número de átomos y el número de enlaces. Encontramos que la coordinación masiva aparece para capas donde t =2 o 3, y como tal es mucho más delgado de lo que se sintetiza normalmente. Los beneficios de la baja coordinación solo se logran para paredes muy delgadas. Esperamos que estos resultados sean útiles para el modelado y el trabajo experimental.

Disponibilidad de datos y materiales

Los conjuntos de datos que respaldan las conclusiones de este artículo pueden obtenerse del autor correspondiente.

Abreviaturas

bcc:

Cúbico centrado en el cuerpo

fcc:

Cúbico centrado en la cara

hcp:

Empaquetado hexagonal cerrado

DFT:

Teoría funcional de la densidad

ELLA:

Electrodo de hidrógeno secundario

Evaluación cuantitativa de la internalización celular de nanopartículas poliméricas dentro de las células del cáncer de laringe y las células inmunes para mejorar la administración de fármaco… Un fotodetector doble de cuatro cuadrantes basado en un nanómetro mejorado de infrarrojo cercano de silicio negro