Comprender las fórmulas de entrenamiento y la retropropagación para perceptrones multicapa

Este artículo presenta las ecuaciones que usamos al realizar cálculos de actualización de peso y también discutiremos el concepto de retropropagación.

Bienvenido a la serie de AAC sobre aprendizaje automático.

Ponte al día con la serie hasta ahora aquí:

1. Cómo realizar la clasificación mediante una red neuronal:¿Qué es el perceptrón?
2. Cómo utilizar un ejemplo de red neuronal de Perceptron simple para clasificar datos
3. Cómo entrenar una red neuronal de perceptrón básica
4. Comprensión del entrenamiento de redes neuronales simples
5. Introducción a la teoría del entrenamiento para redes neuronales
6. Comprensión de la tasa de aprendizaje en redes neuronales
7. Aprendizaje automático avanzado con el perceptrón multicapa
8. La función de activación sigmoidea:activación en redes neuronales de perceptrones multicapa
9. Cómo entrenar una red neuronal de perceptrón multicapa
10. Comprender las fórmulas de entrenamiento y la retropropagación para perceptrones multicapa
11. Arquitectura de red neuronal para una implementación de Python
12. Cómo crear una red neuronal de perceptrón multicapa en Python
13. Procesamiento de señales mediante redes neuronales:validación en el diseño de redes neuronales
14. Conjuntos de datos de entrenamiento para redes neuronales:cómo entrenar y validar una red neuronal Python

Hemos llegado al punto en el que debemos considerar cuidadosamente un tema fundamental dentro de la teoría de redes neuronales:el procedimiento computacional que nos permite ajustar los pesos de un perceptrón multicapa (MLP) para que pueda clasificar con precisión las muestras de entrada. Esto nos llevará al concepto de "retropropagación", que es un aspecto esencial del diseño de redes neuronales.

Actualización de pesos

La información sobre la formación de MLP es complicada. Para empeorar las cosas, los recursos en línea usan terminología y símbolos diferentes, e incluso parecen producir resultados diferentes. Sin embargo, no estoy seguro de si los resultados son realmente diferentes o simplemente presentan la misma información de diferentes formas.

Las ecuaciones contenidas en este artículo se basan en las derivaciones y explicaciones proporcionadas por el Dr. Dustin Stansbury en esta publicación de blog. Su tratamiento es el mejor que encontré, y es un excelente lugar para comenzar si desea profundizar en los detalles matemáticos y conceptuales del descenso de gradientes y la retropropagación.

El siguiente diagrama representa la arquitectura que implementaremos en el software, y las ecuaciones a continuación corresponden a esta arquitectura, que se analiza con más detalle en el siguiente artículo.

Terminología

Este tema rápidamente se vuelve inmanejable si no mantenemos una terminología clara. Usaré los siguientes términos:

• Preactivación (abreviado \ (S_ {preA} \) ):Se refiere a la señal (en realidad, solo un número dentro del contexto de una iteración de entrenamiento) que sirve como entrada para la función de activación de un nodo. Se calcula realizando un producto escalar de una matriz que contiene pesos y una matriz que contiene los valores que se originan en los nodos de la capa anterior. El producto escalar es equivalente a realizar una multiplicación por elementos de las dos matrices y luego sumar los elementos de la matriz resultante de esa multiplicación.
• Postactiviación (abreviado \ (S_ {postA} \) ):Esto se refiere a la señal (nuevamente, solo un número dentro del contexto de una iteración individual) que sale de un nodo. Se produce aplicando la función de activación a la señal de preactivación. Mi término preferido para la función de activación, indicado por \ (f_ {A} () \) , es logístico en lugar de sigmoidea.
• En el código Python, verá matrices de peso etiquetadas con ItoH y HtoO . Utilizo estos identificadores porque es ambiguo decir algo como "pesos de capa oculta":¿serían estos los pesos que se aplican antes la capa oculta o después la capa oculta? En mi esquema, ItoH especifica los pesos que se aplican a los valores transferidos desde los nodos de entrada a los nodos ocultos, y HtoO especifica los pesos que se aplican a los valores transferidos desde los nodos ocultos al nodo de salida.
• El valor de salida correcto para una muestra de entrenamiento se denomina objetivo y se indica con T .
• Tasa de aprendizaje se abrevia como LR .
• Error final es la diferencia entre la señal de postactivación del nodo de salida ( \ (S_ {postA, O} \) ) y el objetivo, calculado como \ (FE =S_ {postA, O} - T \) .
• Señal de error ( \ (S_ {ERROR} \) ) es el error final que se propaga hacia la capa oculta a través de la función de activación del nodo de salida.
• Degradado representa la contribución de un peso dado a la señal de error. Modificamos los pesos restando esta contribución (multiplicada por la tasa de aprendizaje si es necesario).

El siguiente diagrama sitúa algunos de estos términos dentro de la configuración visualizada de la red. Lo sé, parece un desastre multicolor. Me disculpo. Es un diagrama denso en información y, aunque puede resultar un poco ofensivo a primera vista, si lo estudia detenidamente, creo que le resultará muy útil.

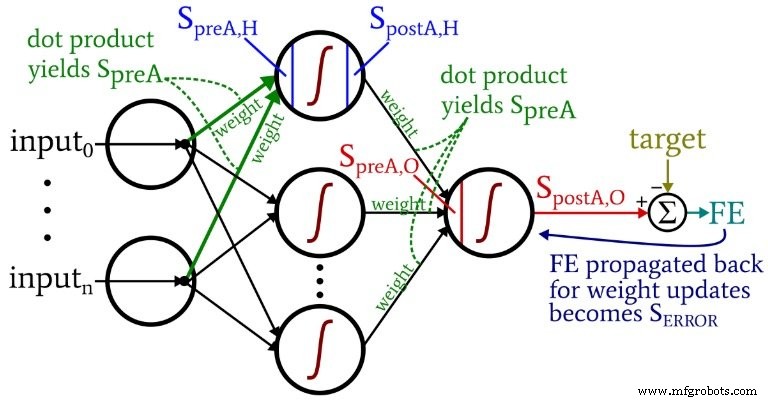
Las ecuaciones de actualización de peso se obtienen tomando la derivada parcial de la función de error (estamos usando el error cuadrático sumado, ver la Parte 8 de la serie, que trata sobre las funciones de activación) con respecto al peso que se va a modificar. Consulte la publicación del Dr. Stansbury si desea ver las matemáticas; En este artículo, pasaremos directamente a los resultados. Para los pesos ocultos a la salida, tenemos lo siguiente:

\ [S_ {ERROR} =FE \ times {f_A} '(S_ {preA, O}) \]

\ [gradient_ {HtoO} =S_ {ERROR} \ times S_ {postA, H} \]

\ [peso_ {HtoO} =peso_ {HtoO} - (LR \ times gradient_ {HtoO}) \]

Calculamos la señal de error l multiplicando el error final por el valor que se produce cuando aplicamos la derivada de la función de activación a la señal de preactivación entregado al nodo de salida (observe el símbolo principal, que indica la primera derivada, en \ ({f_A} '(S_ {preA, O}) \)). El gradiente luego se calcula multiplicando la señal de error por la señal de postactivación de la capa oculta. Finalmente, actualizamos el peso restando este gradiente del valor de peso actual, y podemos multiplicar el gradiente según la tasa de aprendizaje si queremos cambiar el tamaño del paso.

Para los pesos de entrada a ocultos, tenemos esto:

\ [gradient_ {ItoH} =FE \ times {f_A} '(S_ {preA, O}) \ times weight_ {HtoO} \ times {f_A}' (S_ {preA , H}) \ times input \]

\ [\ Rightarrow gradient_ {ItoH} =S_ {ERROR} \ times weight_ {HtoO} \ times {f_A} '(S_ {preA, H}) \ times input \]

\ [peso_ {ItoH} =peso_ {ItoH} - (LR \ times gradient_ {ItoH}) \]

Con las ponderaciones de entrada a oculta, el error debe propagarse a través de una capa adicional, y lo hacemos multiplicando la señal de error por el peso oculto para la salida conectado al nodo oculto de interés. Por lo tanto, si estamos actualizando un peso de entrada a oculto que conduce al primer nodo oculto, multiplicamos la señal de error por el peso que conecta el primer nodo oculto al nodo de salida. Luego completamos el cálculo realizando multiplicaciones análogas a las de las actualizaciones de peso ocultas para generar:aplicamos la derivada de la función de activación a la señal de preactivación del nodo oculto , y el valor de "entrada" se puede considerar como la señal de postactivación desde el nodo de entrada.

Retropropagación

La explicación anterior ya ha tocado el concepto de retropropagación. Solo quiero reforzar brevemente este concepto y también asegurarme de que esté familiarizado explícitamente con este término, que aparece con frecuencia en las discusiones sobre redes neuronales.

La retropropagación nos permite superar el dilema del nodo oculto discutido en la Parte 8. Necesitamos actualizar las ponderaciones de entrada a oculta en función de la diferencia entre la salida generada por la red y los valores de salida objetivo proporcionados por los datos de entrenamiento, pero estas ponderaciones influyen la salida generada indirectamente.

La retropropagación se refiere a la técnica mediante la cual enviamos una señal de error hacia una o más capas ocultas y escalamos esa señal de error utilizando tanto los pesos que emergen de un nodo oculto como la derivada de la función de activación del nodo oculto. El procedimiento general sirve como una forma de actualizar un peso basado en la contribución del peso al error de salida, aunque esa contribución se ve oscurecida por la relación indirecta entre un peso de entrada a oculto y el valor de salida generado.

Conclusión

Hemos cubierto mucho material importante. Creo que tenemos información realmente valiosa sobre el entrenamiento de redes neuronales en este artículo, y espero que esté de acuerdo. La serie comenzará a ser aún más emocionante, así que vuelva a consultar las nuevas entregas.