Relaciones matemáticas mágicas para nanoclusters
Resumen
El tamaño y las propiedades de la superficie, como la catálisis, la fotoluminiscencia óptica de puntos cuánticos y las resonancias de plasmones superficiales, dependen de la coordinación y química de los nanoclusters semiconductores y de metales. Tales propiedades dependientes de la coordinación se cuantifican aquí mediante "fórmulas mágicas" para el número de conchas, n , en el clúster. Investigamos cúbicos centrados en las caras, cúbicos centrados en el cuerpo, cúmulos cúbicos simples, cúmulos hexagonales compactos y la estructura cúbica de diamante en función del número de conchas de cúmulos, n . Además, examinamos los sólidos platónicos en forma de grupos de múltiples capas, para un total de 19 tipos de grupos. La cantidad de enlaces, átomos y números de coordinación exhiben características de números mágicos versus n , a medida que aumenta el tamaño de los conglomerados. Comenzando solo con las coordenadas espaciales, creamos una matriz de adyacencia y distancia que facilita el cálculo de índices topológicos, incluidos los índices de Wiener, hyper-Wiener, Wiener inverso y Szeged. Algunas fórmulas topológicas conocidas para algunos sólidos platónicos cuando n =1 se verifican computacionalmente. Estos índices tienen fórmulas mágicas para muchos de los grupos. La estructura cúbica simple es la menos compleja de nuestros grupos, medida por la complejidad topológica derivada del contenido de información de la distribución de grados de vértice. La dispersión, o porcentaje relativo de átomos de superficie, se mide cuantitativamente con respecto a la dependencia del tamaño y la forma para algunos tipos de grupos con aplicaciones catalíticas.
Introducción
Los números y fórmulas mágicos para nanoclusters tienen una larga historia que se remonta a la publicación profética de van Hardeveld y Hartog en 1969 [1]. Sus conocimientos son anteriores a la era de la nanociencia. Desde entonces, hemos visto aparecer números mágicos en polígonos 2D y poliedros 3D [2], fullerenos de carbono [3], y en un alcance limitado nuevamente en grupos [4]. Materiales tan diversos como el silicio [5], el boro [6] y, de hecho, más de 1000 publicaciones del servicio de indexación “Web of Science” se refieren a números mágicos en grupos. El estudio del tamaño y la forma de los nanoclusters es importante para la sociedad actual, ya que esto determina no solo las propiedades físicas y químicas intrínsecas, sino también la relevancia para las aplicaciones ópticas, catalíticas, electrónicas y magnéticas [7]. Nuestro objetivo es actualizar la base de datos de este conocimiento con las relaciones y los datos actuales, ahora que hemos entrado en el ámbito nano.
La aparición de números mágicos en nanoclusters tiene que ver principalmente con la formación de capas de átomos en una célula fundamental. Cuando el número de átomos completa una capa completa, encontramos un conjunto único de números, denominado "magia", que define las capas de los átomos. Un grupo está representado por un gráfico con los átomos como vértices y los enlaces como aristas. Consiste en cáscaras anidadas como capas de cebolla. Definimos el número de capas como n y descubrir las relaciones matemáticas de los números de coordinación del vecino más cercano, los enlaces, el número total de átomos y algunos índices topológicos en función de n . El artículo original de van Hardeveld y Hartog [1] consideró agrupaciones fcc, bcc y hcp. La referencia de Teo y Sloane [2] considera poliedros y sólidos platónicos, pero ignora la relación de los números de coordinación del vecino más cercano. Agregamos a esta base de datos al observar los sólidos cúbicos simples, cúbicos de diamantes y platónicos, además de las propiedades topológicas y la dispersión de los grupos.
La transición de tamaño de la masa a los grupos de unos pocos átomos se trata realmente de la relación de los átomos de la superficie en comparación con los átomos de la masa. Propiedades como la química catalítica, la resonancia de plasmón superficial y la fotoluminiscencia óptica de puntos cuánticos [8] se ven afectadas por la coordinación y el número de átomos de superficie. La dispersión o porcentaje relativo de átomos de superficie se determina mediante la relación entre los átomos de superficie y el número total de átomos, como se ha considerado anteriormente [9]. Nuestro análisis determinará la clasificación relativa de la dispersión en términos de geometría de conglomerados.
Los índices topológicos comenzaron con el artículo original de Wiener sobre su índice y los puntos de ebullición de la parafina [10]. No fue hasta algún tiempo después que Hosoya introdujo un formalismo matemático para analizar índices topológicos [11]. Hemos introducido previamente índices topológicos y nanoclusters [12]. En el momento de escribir este artículo, existen muchos índices, algunos de los cuales dependen de la matriz de adyacencia o distancia. Mostramos aquí que en muchas de las formas de grupos, existen relaciones matemáticas mágicas para los cuatro índices en función de n y el número de proyectiles.
Métodos
Para cada uno de los tipos de conglomerados que estudiamos, creamos un algoritmo computacional que determina las coordenadas atómicas de los conglomerados. Luego procedemos a crear una matriz de adyacencia y una matriz de distancia definida como sigue. Una matriz de adyacencia A se crea donde definimos i y j como vecinos más cercanos y sepárelos del resto exigiendo que r ij < r c , donde r c es un valor de umbral, ligeramente por encima de la distancia del vecino más cercano, pero menor que la distancia del segundo vecino. Por lo tanto,
$$ \ mathbf {A} (i, j) =\ left \ {\ begin {array} {l} 1 ~~ \ text {if} ~ r_ {ij}donde d ij es la longitud de la ruta más corta en el gráfico de i a j . Existe un algoritmo eficiente para el cálculo de la matriz de distancias desde la matriz de adyacencia [13]. Usando estas definiciones, podemos calcular el índice de Wiener, W ( G ), el índice Hyper-Wiener, W W ( G ), el índice de Wiener inverso rW ( G ) y el índice de Szeged, Sz ( G ), como se detalló anteriormente [14]. Estos cálculos utilizan el mismo algoritmo que hemos utilizado anteriormente para índices topológicos y nanoclusters [12].
Autores anteriores han ofrecido pruebas de relaciones mágicas, que condensamos en nuestra notación, relevantes para el trabajo aquí presentado [1, 2]. Dado que creamos matrices de adyacencia vecinas más cercanas, conocemos el número de coordinación c n i del vértice i sumando los elementos de A ( yo , :). Nuestra estructura consta de n +1 conchas numeradas 0,1,…, n . Sea \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) el número de átomos con coordinación c n i donde 1≤ c n i ≤ c n M con c n M la máxima coordinación en el cluster. Entonces, el número total de átomos en el grupo viene dado por
$$ N_ {T} (n) =\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {N _ {{cn} _ {i}} (n)}. $$ (3)Los átomos de la superficie en la capa exterior n tienen un conjunto de enlaces menor que la coordinación a granel. Por lo tanto, la coordinación máxima para los átomos de la superficie es c n s < c n M , y el número de átomos de superficie es
$$ N_ {S} (n) =\ sum _ {{cn} _ {i} =1} ^ {{cn} _ {s}} {N _ {{cn} _ {i}} (n)}. $$ (4)Esto es válido si todos los vértices que no son de superficie tienen una coordinación mayor que c n s , que es cierto para todos los grupos, pero tenga en cuenta la discrepancia para el dodecaedro a continuación. Determinamos \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) contando las columnas de la matriz de adyacencia cuya suma es c n i . Tenga en cuenta que nuestro algoritmo de coordenadas de clúster está construido por shells, por lo que cada shell subsiguiente contiene todos los valores inferiores anteriores de n . En la Fig. 1, ilustramos las conchas de los grupos de un cubo fcc y un dodecaedro. Además, la cantidad de enlaces en el clúster es
$$ N_ {B} (n) =\ frac {1} {2} \ sum _ {{cn} _ {i} =1} ^ {{cn} _ {M}} {{cn} _ {i} \ cdot N _ {{cn} _ {i}} (n)}, $$ (5)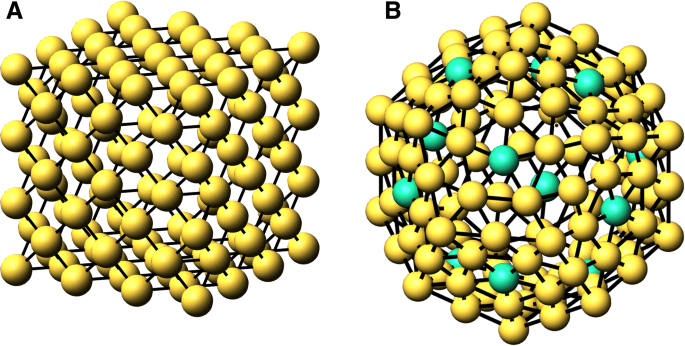
Caparazones de átomos para n =3 para A. fcc cube y n =2 B. dodecaedro. En B, los átomos verdes (12) se refieren a c n =5 dentro del caparazón
donde N B ( n ) es el número de enlaces y c n M es la máxima coordinación. El factor 1/2 se produce debido a la vinculación del vecino más cercano por pares. Esta relación mágica parece no haber sido considerada en publicaciones anteriores, con la excepción de algunos grupos examinados en [4]. También comentamos que Teo y Sloane han derivado el número total de átomos, átomos de la superficie y átomos interiores de los cúmulos de la siguiente manera [2]:
$$ N_ {T} (n) =\ alpha n ^ {3} + \ frac {1} {2} \ beta n ^ {2} + \ gamma n + 1 ~~ n \ ge {0} $$ ( 6)donde N T ( n ) es el número total de átomos, y
$$ \ alpha =C / 6 $$ (7)donde C es el número de celdas tetraédricas en las que se divide el poliedro, y
$$ \ beta =1 / 2F_ {s} $$ (8)donde F s es el número de caras triangulares en la superficie, y
$$ \ gamma =F_ {s} / 4 + V_ {i} + 1-C / 6 $$ (9)donde V i es el número de vértices en el interior. También muestran que
$$ N_ {S} (n) =\ beta n ^ {2} + 2 ~~ n \ ge {1}; ~~ N_ {S} (0) =1 $$ (10)y
$$ N_ {I} (n) =N_ {T} (n) - N_ {S} (n), $$ (11)donde N yo ( n ) es el número de átomos interiores. Esta información (ecuación (11)) está contenida en la matriz de adyacencia, así como en las ecuaciones. (3, 4, 5). Estas ecuaciones son una verificación de los resultados de los datos de la matriz de adyacencia. Para poliedros centrados, también tenemos
$$ N_ {I} (n) =N_ {T} (n-1), $$ (12)y de Eq. (11), tenemos
$$ N_ {T} (n) =N_ {S} (n) + N_ {S} (n-1) + ... + N_ {S} (1) + N_ {S} (0). $$ (13)A partir de estas ecuaciones, podemos derivar las fórmulas mágicas para cada uno de los grupos de la siguiente manera. Después de calcular la matriz de adyacencia topológica (0,1) A para un clúster con n conchas como se describe, sabemos que su tamaño N = N T ( n ) indica el número total de átomos. La suma de las entradas en la columna i da el número de enlaces c n i ( n ) para el átomo i y contando el número de sumas de columnas iguales a c n i ( n ) da obviamente \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \). Como sabemos que estos dependen de n como un polinomio de grado como máximo 3, podemos calcular N T ( n ) y c n i ( n ) para 4 valores consecutivos de n , di n = n 0 + j , j =0,1,2,3. Entonces, un polinomio de interpolación simple dará los coeficientes del polinomio. Debe verificarse que aumentando n 0 , que suele ser igual a 1, las fórmulas no cambian. Si las fórmulas se estabilizan desde n 0 en, luego se mantienen para todos n ≥ n 0 . En algunos casos, la relación polinomial solo es válida para los pares n valores o los impares. Por ejemplo, para el dodecaedro rómbico fcc (Tabla 1), las capas sucesivas tienen ocho átomos con coordinación 3 cuando n ≥2 es par, y ninguno si n es impar. En tales casos, se mantendrán diferentes relaciones polinomiales para n par y n extraño, pero los datos se utilizan para n = n 0 + j , j =0,2,4,6 con n 0 impar (por ejemplo, n 0 =1) o n 0 incluso ( n 0 =2). Para obtener los coeficientes racionales exactos, es necesario resolver el sistema de Vandermonde para los coeficientes en aritmética exacta utilizando la caja de herramientas simbólicas de MATLAB. Así es como se calculan las Tablas 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 y 19. En la siguiente sección, determinamos fórmulas mágicas para N T ( n ), N B ( n ) y para \ (\ phantom {\ dot {i} \!} N _ {{cn} _ {i}} (n) \) de acuerdo con la receta prescrita.
La dispersión (fracción expuesta, FE) de los átomos de la superficie se define como:
$$ \ text {FE} =\ frac {N_ {S}} {N_ {T}} \ cdot 100 \% $$ (14)donde N S es el número de átomos de la superficie, y N T es el número total de átomos [9]. Podemos comparar clústeres diferentes definiendo el tamaño relativo del clúster como:
$$ d_ {rel} =b (N_ {T}) ^ {1/3}; ~~ b =d_ {at} ^ {- 1} \ cdot \ left (\ frac {6V_ {u}} {\ pi n_ {u}} \ derecha) ^ {1/3} $$ (15)donde d en es el diámetro atómico covalente, V u es el volumen de la celda unitaria y n u es el número de átomos en la celda unitaria. La constante de estructura cristalina b es igual a 1,105 para las agrupaciones fcc y hcp, 1,137 para las agrupaciones bcc [1], 1,488 para las agrupaciones cúbicas simples y 1,517 para las agrupaciones cúbicas de diamantes. Como se muestra arriba, la fórmula para FE es una relación de un cuadrático a un cúbico para los conglomerados y se puede modelar mediante un ajuste de curva de ley de potencia versus d rel . La variable d rel nos permite comparar diferentes grupos entre sí sin tener en cuenta la estructura cristalina. Para algunos de los grupos platónicos, donde no hay una celda unitaria de cristal, usamos \ (N_ {T} ^ {1/3} \) como variable.
Resultados y discusión
El estudio del tamaño y la forma de los nanoclusores metálicos ha evolucionado desde su infancia hace dos décadas. La Tabla 20 muestra algunos avances relevantes a 2018.
En la Tabla, enumeramos principalmente metales de transición, no aleaciones o compuestos, con la excepción de la bipirámide hexagonal truncada, donde solo Fe 2 O 3 fue encontrado. Ha habido más síntesis de racimos de oro que cualquier otro elemento, debido a sus propiedades y estabilidad. En las subsecciones que siguen, limitamos nuestra discusión a temas específicos relacionados con fórmulas mágicas y tipos de agrupaciones.
Clústeres de FCC
Ocho de los metales de transición cristalizan en la estructura fcc, véase la Tabla 21 a continuación, incluidos los metales nobles plasmónicos y los elementos catalíticamente activos importantes. La gran mayoría de la síntesis de nanocluster se ha realizado con estos elementos. En la Tabla 21 se dan referencias de la síntesis de los elementos fcc con varias formas y tamaños.
Las aleaciones de estos elementos también son de interés, pero las referencias a estos son demasiado numerosas para citarlas aquí. Con frecuencia, las formas comunes que se sintetizan son cubos, octaedros, cuboctaedros e icosaedros. Normalmente, las agrupaciones con facetas (111) son más fáciles de sintetizar, ya que la superficie (111) suele tener una energía menor que la superficie (100) [7]. Encontramos para el dodecaedro rómbico fcc que existen fórmulas pares e impares. Estos concuerdan con los de [1], si uno reemplaza el " n "En nuestras fórmulas pares por 2 ( m −1). Las fórmulas para cuboctaedros fcc enumeradas en [24] producen los mismos números mágicos que los nuestros, pero se desplazan en 1 ya que numeran las conchas como n =1,2,… y usamos la numeración n =0,1,…. Nuestras fórmulas mágicas concuerdan con las de [2, 4], y en deferencia al trabajo publicado anteriormente, y para mantener la continuidad de las matemáticas, usamos la notación [2, 4]. Las 5 formas de clúster fcc y sus fórmulas mágicas asociadas aparecen a continuación.
Clústeres CCO
Siete de los metales de transición en la tabla periódica tienen la estructura bcc, ver Tabla 21. De los elementos magnéticos Fe, Co y Ni, solo el hierro es bcc. Los nanocubos de hierro parecen ser la única forma de racimo de bcc sintetizada hasta ahora [25]. Aunque la estructura general del hierro es bcc, se han sintetizado nanoclusters de fcc [26]. Esta referencia también analiza la estabilidad termodinámica de los racimos. Aquí presentamos 5 formas de clúster de bcc y sus fórmulas mágicas asociadas.
Grupos de HCP
Doce metales de transición tienen la estructura hcp, ver Tabla 21. Sin embargo, muchos de estos se oxidan o carecen de un interés científico convincente para ser sintetizados. Con respecto a la forma de racimo bipiramidal hexagonal en la Tabla 11, se han sintetizado los racimos de oro [27]. La bipirámide hexagonal truncada relacionada parece haber sido formada solo por α −Fe 2 O 3 [28].
Clústeres platónicos
Los sólidos platónicos se conocen desde los antiguos griegos. Incluyen el cubo, tetraedro, octaedro, icosaedro y dodecaedro. En tablas anteriores, hemos enumerado fórmulas mágicas para cubos y octaedros fcc y bcc. Aquí enumeramos las fórmulas para el icosaedro, el dodecaedro, el tetraedro y el tetraedro centrado en el cuerpo. Como se mencionó anteriormente en la sección "Métodos", el dodecaedro es único para los grupos analizados aquí, en que c n s =7 se refiere tanto a los átomos superficiales como a los voluminosos. Mostramos en la Fig. 1b que la capa exterior contiene átomos coordinados quíntuple y séxtuple. Cuando una capa se vuelve interna, esos átomos coordinados cinco y seis veces se vuelven coordinados siete y ocho veces con enlaces a una capa a cada lado. Además, los átomos de la capa exterior seis veces coordinados se coordinan siete veces al unirse a la capa interior. Por lo tanto, hay siete átomos coordinados en superficie y en masa para el dodecaedro. Cada capa de la estructura tiene 12 átomos de capa quíntuple, que producen 12 n −12 átomos coordinados séptuples a granel. El resto de la coordinación séptuple son átomos de superficie.
Se ha demostrado que los nanoclusters de oro adoptan formas platónicas [29]. Esta referencia incluye el cubo, el tetraedro, el octaedro y el icosaedro. Más tarde, también se sintetizó el nanocluster dodecaedro dorado [30]. Aquí, mostramos tanto el tetraedro regular, que es "similar a fcc" en ese c M =12 como en las estructuras fcc, y el tetraedro centrado en el cuerpo en la Tabla 16, donde los átomos verdes tienen enlaces simples. Las fórmulas mágicas platónicas se presentan a continuación.
Clústeres de diamantes cúbicos, cúbicos simples y decaedros
Los elementos silicio y germanio tienen la red cúbica de diamante, así como el alótropo de carbono de diamante. En particular, el silicio terminado en hidrógeno ha recibido un interés reciente. Se ha determinado que la superficie terminada en hidrógeno (100), que da lugar a formas cúbicas en grupos, tiene la energía más baja [31]. Se ha logrado la síntesis de nanocubos de Si-H de 8-15 nm de tamaño [32]. La Tabla 17 muestra un diagrama de los grupos de Si-H terminados en hidrógeno, con átomos de hidrógeno de enlace simple en verde. Si un nanocluster toma la forma cúbica de diamante, habrá enlaces colgantes individuales, que deben pasivarse para ayudar a mantener la estructura. Al observar las fórmulas mágicas, sugerimos que la composición de dichos grupos Si-H es \ (\ phantom {\ dot {i} \!} \ Text {Si} _ {8n ^ {3} + 6n ^ {2} -9n +5} \ text {H} _ {12n-8} \), donde n es el número de conchas en el grupo. Estos puntos cuánticos semiconductores pueden ser de interés para las propiedades ópticas, y se ha determinado que la variación en la banda prohibida con el tamaño de los grupos terminados en hidrógeno es inversamente proporcional al tamaño del grupo [33].
La estructura de celosía cúbica simple ha sido previamente analizada por otros [4], aunque sin el detalle que proporcionamos. Hemos estudiado previamente el d -formas hipercubo dimensionales [14]. El polonio es el único elemento que adopta la estructura cúbica simple. Es radiactivo, lo que puede dar lugar a aplicaciones especializadas. Aquí presentamos las fórmulas mágicas de racimo de diamante cúbico, cúbico simple y decaédrico.
Fórmulas topológicas mágicas
La complejidad estructural medida en cristales puede darnos una idea de la simplicidad o complejidad de la estructura y el uso adecuado puede clasificar estructuras relevantes. Para tales clasificaciones, es útil considerar la descripción gráfica de la red cristalina, como se menciona en la sección "Métodos". La complejidad topológica de las estructuras cristalinas se mide mediante la distribución de grados de vértice del gráfico, I vd [34], utilizando el software ToposPro, versión 5.3.2.2 [35]:
$$ I_ {vd} =\ sum_ {i =1} ^ {v} a_ {i} \ cdot {\ text {log} _ {2}} \ {a_ {i}} $$ (16)donde a i es el grado (coordinación) del i El vértice y la suma avanzan a lo largo de todo v vértices, del gráfico del cociente. Este parámetro utiliza un cristal infinito a diferencia de los grupos que hemos estado considerando, pero es útil para medir la complejidad relativa de diferentes estructuras cristalinas. Por lo tanto, cuanto mayor sea el número, o cuanto más contenido de información en el gráfico, más complejo es. En la Tabla 22, mostramos los valores de I vd obtenido de ToposPro derivado de archivos cif para estructuras cristalinas en Crystallographic Open Database. El polonio es el único elemento que cristaliza en la estructura cúbica simple y el valor es cero, es decir, el gráfico del cociente tiene un vértice y aristas cero, de acuerdo con lo que esperamos, que la estructura cúbica simple es efectivamente la estructura menos compleja. También se muestra la sal, NaCl, con dos elementos en la estructura cúbica simple, junto con silicio en la estructura cúbica de diamante, oro en fcc, hierro en bcc y cobalto en estructuras hcp. Mencionamos que otra medida de complejidad relacionada con la entropía de Shannon [34] no es útil porque esta medida para todos los elementos es idénticamente cero.
Se puede aplicar un método similar al descrito en la sección "Métodos" para determinar fórmulas mágicas para las fórmulas mágicas que describen los índices topológicos. Solo aquí, los grados de los polinomios son 7, 8 o 9, por lo que sus valores durante al menos 10 n consecutivos -Los valores deben calcularse. Entonces, un problema de interpolación de mayor grado da el resultado. Dado que resolver un sistema lineal de tamaño 10 × 10 con la caja de herramientas simbólica requiere algo de tiempo, todos los coeficientes de los índices topológicos se pueden calcular simultáneamente utilizando múltiples lados derechos para obtener los coeficientes de todos los polinomios.
Las fórmulas mágicas para los índices topológicos se detallan en las Tablas 23, 24 y 25. Los cuatro índices que analizamos dependen solo de n , el número de conchas en el grupo. Mirando los resultados, la celosía cúbica simple como la estructura menos compleja, también tiene las fórmulas “más simples”. A pesar de nuestros esfuerzos, no podemos resolver el índice de Szeged de cubos bcc. No se encontró una solución estable. En general, las estructuras fcc son más fáciles de resolver para fórmulas topológicas. No pudimos resolver ninguna estructura hcp y solo algunas estructuras bcc. Esto puede estar relacionado con la complejidad topológica, ya que la red fcc es más simple que la bcc o hcp, consulte la Tabla 22. En las tablas, proporcionamos fórmulas para el cuboctaedro, el icosaedro y el decaedro. Anteriormente [12] proporcionamos tablas de datos numéricos para estos índices, con la salvedad de que el cuboctaedro en [12] tenía diferentes números mágicos. Aquí vemos que los datos tabulados pueden resumirse sucintamente como fórmulas mágicas. Además, el grado del polinomio del índice sigue las reglas del espacio 3D [14]. Se han publicado previamente algunos índices topológicos para los sólidos platónicos [36]. A partir de esta referencia, verificamos el índice de Wiener para los cinco sólidos para n =1. Se ha estudiado el índice de Wiener para filas de celdas unitarias de la red fcc [37], pero nuestros resultados no se pueden comparar ya que estudiamos conglomerados.
Dispersión
El porcentaje de átomos de superficie (dispersión, FE) de los diversos clusters se presenta en la Fig. 2. Se sabe que los nanoclusters de platino tienen actividad catalítica con respecto a la reacción de reducción de oxígeno (ORR) que depende del tamaño y la forma [38]. Esta referencia determinó que los grupos cuboctaédricos de platino de 2,2 nm de tamaño tenían una actividad de ORR máxima. También se sabe que para las aleaciones de PtNi se prefiere la superficie (111) para el ORR [39]. Comparamos los grupos icosaédricos, octaédricos, decaédricos y cuboctaédricos para FE en un d rel =7,5 para platino a 2,2 nm. Los grupos icosaédricos, octaédricos y decaédricos tienen superficies con (111) caras. Usando las leyes de potencia en la Fig. 2, encontramos para el d dado rel que la FE para los cúmulos icosaédricos es 47,9%, para los cuboctaédricos 52,8% y para los decaédricos 57,5% y que los cúmulos octaédricos tienen FE =58,9 % . Por lo tanto, según la forma, los grupos octaédricos tienen tanto la superficie (111) como el valor más alto de FE para un tamaño similar. Tanto el coeficiente de la ley de potencia como el exponente son relevantes para la determinación de FE para pequeños d rel . La interpretación matemática del exponente de la ley de potencia da el significado físico como la relación de la ordenada, FE, con las abscisas, d rel , o el cambio porcentual relativo de FE al cambio porcentual relativo de d rel . El coeficiente de la ley de potencia es simplemente el valor de FE cuando d rel =1.
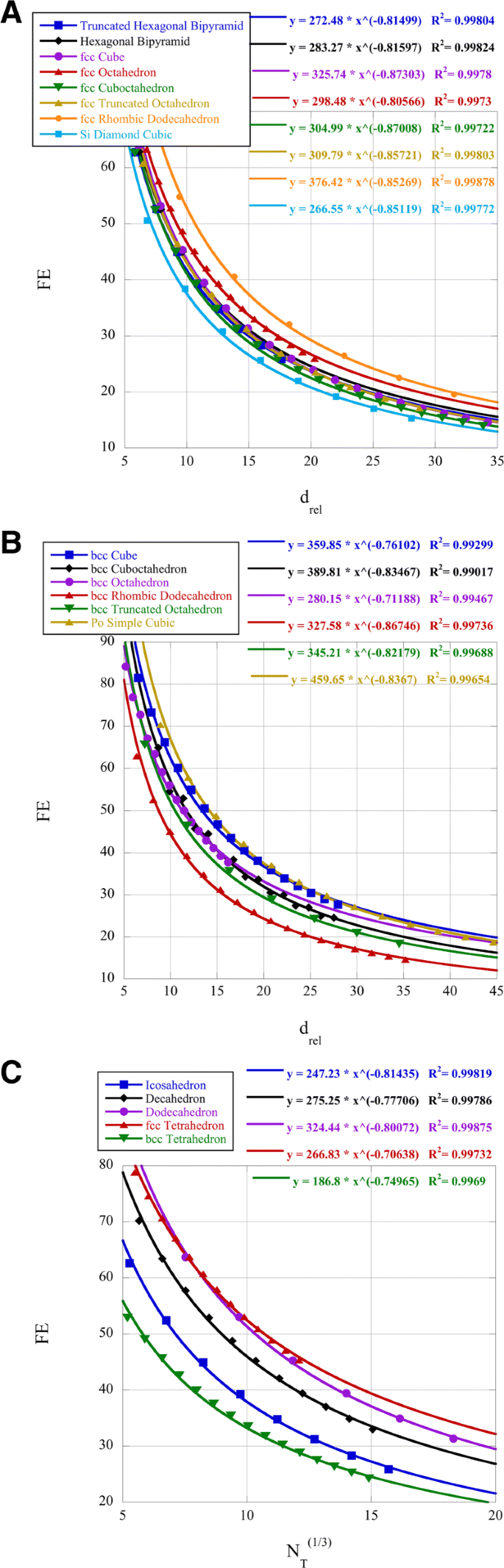
Dispersión FE para los nanoclusters
Otro grupo de investigación ha sintetizado grupos icosaédricos de aleación de platino y ha comparado la actividad con los octaédricos [40]. Estos nanoclusters tenían un tamaño de aproximadamente 13 nm o N =20.000 para grupos octaédricos y N =15.000 para grupos icosaédricos. Esto produce un d rel =30 para los racimos octaédricos y 25 para los icosaédricos. Usando las leyes de potencia relevantes, esto da FE =18.0 % para el octaédrico y 19,8% para los cúmulos icosaédricos. Hay muy poca diferencia en FE para este tamaño del grupo, pero el grupo icosaédrico tiene una cantidad significativa de tensión debido al hermanamiento, que puede desplazar el centro de la banda d, afectando así los resultados de la ORR [40]. Sin embargo, dados los datos dependientes del tamaño de [38], se puede sugerir que los conglomerados más pequeños producirían datos de ORR aún más altos. De hecho, 4 nm Pt 3 Los octaedros de Ni, cuando se doparon con Mo, han producido resultados de ORR récord [41].
Conclusiones
Hemos estudiado 19 tipos de nanoclusters y algunas fórmulas mágicas relevantes para el número de átomos, enlaces, números de coordinación e índices topológicos. Estos incluyen los grupos fcc, bcc, hcp, sólidos platónicos, cúbicos de diamantes, cúbicos simples y decaédricos. La mayoría de estos resultados son más detallados de lo que se determinó anteriormente y un gran número se enumeran por primera vez. Un gran objetivo de la investigación relacionada con los materiales es la correlación de la estructura con las propiedades. Este estudio detallado de las relaciones mágicas de los nanoclusters es un paso en esa dirección. Un ejemplo es la discusión de la dispersión de átomos superficiales y su relación con la actividad catalítica. Nuestra intención es que estos resultados ayuden a los científicos en sus estudios de la estructura de los nanoclusters y las propiedades asociadas.
Abreviaturas
- bcc:
-
cúbico centrado en el cuerpo
- cif:
-
archivo de información cristalográfica
- fcc:
-
cúbico centrado en la cara
- FE:
-
Fracción expuesta, dispersión
- hcp:
-
empaquetado hexagonal cerrado
- ORR:
-
Reacción de oxidación y reducción
- rW (G):
-
Índice de salchicha inversa
- Sz (G):
-
Índice Szeged
- W (G):
-
Índice de Wiener
- WW (G):
-
Índice Hyper-Wiener
Nanomateriales
- C# para bucle
- C para bucle
- Separadores de aire para chips de 10 nm
- Imágenes de átomos en cristales atómicos 2D en líquidos
- Construyendo qubits de un solo átomo bajo un microscopio
- Nanocristales de estaño para futuras baterías
- Recubrimiento nano para varios colores
- Nanoheterouniones para células solares
- Relaciones matemáticas mágicas para nanoagrupaciones:erratas y apéndice
- Fabricación de PCB para 5G
- Nueva herramienta matemática puede seleccionar los mejores sensores para el trabajo



