Teorema de Thévenin. Procedimiento paso a paso con ejemplo resuelto

Teorema de Thevenin en análisis de circuitos de CC

Un ingeniero francés, M.L Thevenin , realizó uno de estos saltos cuánticos en 1893. Teorema de Thevenin  (también conocido como Teorema de Helmholtz-Thévenin ) no es en sí mismo una herramienta de análisis, sino la base de un método muy útil para simplificar circuitos activos y redes complejas. Este teorema es útil para resolver rápida y fácilmente redes y circuitos lineales complejos, especialmente circuitos eléctricos y redes electrónicas.

Teorema de Thevenin puede indicarse a continuación:

• V_TH =Voltaje de Thevenin
• R_TH =Thevenin  Resistencia

Publicación relacionada:Teorema de Norton. Procedimiento sencillo paso a paso con ejemplo (vistas pictóricas)

Pasos para analizar un circuito eléctrico usando el teorema de Thevenin

1. Abra la resistencia de carga.
2. Calcule / mida el voltaje de circuito abierto. Este es el voltaje de Thevenin (V_TH ) .
3. Fuentes de corriente abiertas y fuentes de corto voltaje.
4. Calcule/mida la resistencia de circuito abierto. Esta es la Resistencia de Thevenin (R_TH ) .
5. Ahora, vuelva a dibujar el circuito con el voltaje de circuito abierto medido (V_TH ) en el Paso (2) como fuente de voltaje y la resistencia de circuito abierto medida (R_TH ) en el paso (4) como una resistencia en serie y conecte la resistencia de carga que habíamos quitado en el paso (1). Este es el circuito equivalente de Thevenin de esa red eléctrica lineal o circuito complejo que tuvo que ser simplificado y analizado por el Teorema de Thevenin . Lo has hecho.
6. Ahora encuentre la corriente total que fluye a través de la resistencia de carga usando la Ley de Ohm:I_T =V_TH / (D_TH + D_I ).
   

Publicación relacionada:Análisis de circuito SUPERMESH | Paso a Paso con Ejemplo Resuelto

Ejemplo resuelto por el teorema de Thevenin:

Ejemplo:

Buscar V_TH , R_TH y la corriente de carga I_L que fluye a través y el voltaje de carga a través de la resistencia de carga en la figura (1) utilizando el Teorema de Thevenin .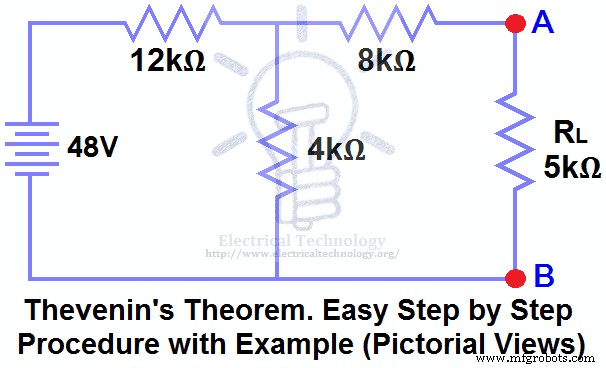

Solución:-

PASO 1.

Abra la resistencia de carga de 5 kΩ (Figura 2).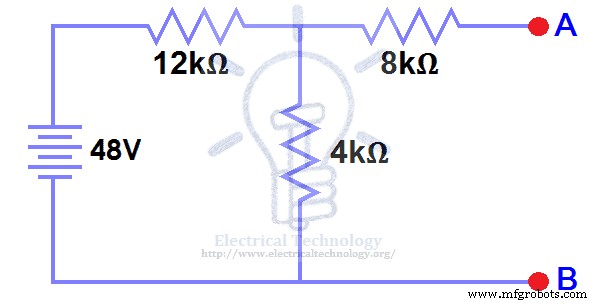

PASO 2.

Calcular/medir el voltaje de circuito abierto. Este es el voltaje de Thevenin (V_TH ) . Fig. 3).

Ya quitamos la resistencia de carga en la figura 1, por lo que el circuito se convirtió en un circuito abierto como se muestra en la figura 2. Ahora tenemos que calcular el voltaje de Thevenin. Desde 3mA flujos de corriente en ambos 12kΩ y 4kΩ resistencias ya que este es un circuito en serie y la corriente no fluirá en los 8kΩ resistencia ya que está abierta.

De esta manera, 12V (3mA x 4kΩ) aparecerá en la resistencia de 4kΩ . También sabemos que la corriente no fluye a través de la resistencia de 8kΩ porque es un circuito abierto, pero la resistencia de 8kΩ está en paralelo con la resistencia de 4k. . Entonces, aparecerá el mismo voltaje, es decir, 12 V en la resistencia de 8 kΩ así como resistencia de 4kΩ. Por lo tanto, aparecerán 12 V en los terminales AB. es decir,

V_TH =12V

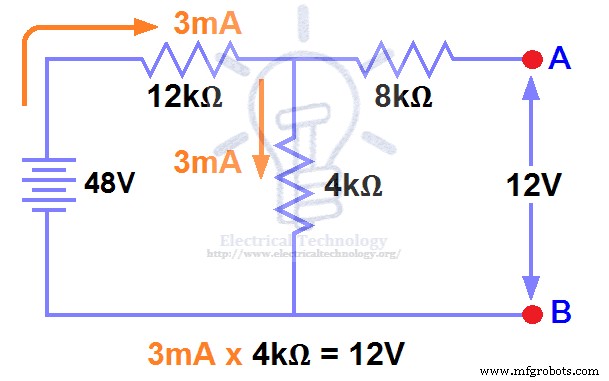
PASO 3.

Fuentes actuales abiertas y fuentes de corto voltaje Como se muestra abajo. Higo (4)

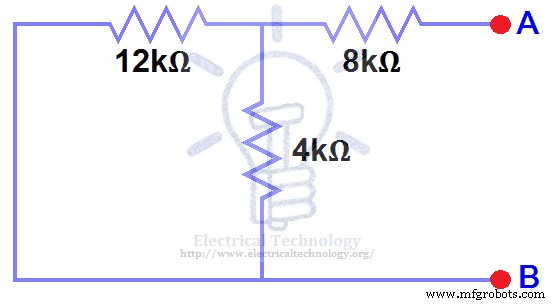
PASO 4.

Calcular / medir la resistencia de circuito abierto . Esta es la Resistencia de Thevenin (R_TH )

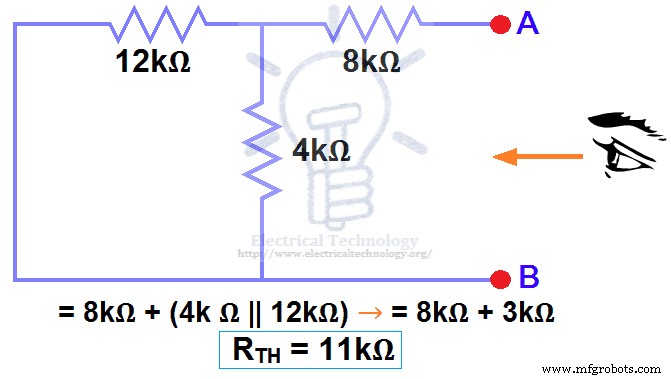
Hemos eliminado la fuente de CC de 48 V a cero como equivalente, es decir, la fuente de 48 VCC se reemplazó con un cortocircuito en el paso 3 (como se muestra en la figura 3). Podemos ver que la resistencia de 8 kΩ está en serie con una conexión en paralelo de una resistencia de 4 kΩ y una resistencia de 12 k Ω. es decir:

8kΩ + (4k Ω || 12kΩ) ….. (|| =en paralelo con)

R_TH =8kΩ +  [(4kΩ x 12kΩ) / (4kΩ + 12kΩ)]

R_TH =8kΩ + 3kΩ

D_TH =11kΩ

PASO 5.

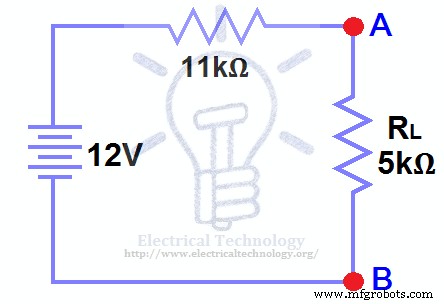
Conecte el R_TH en serie con la fuente de tensión V_TH y vuelva a conectar la resistencia de carga. Esto se muestra en la figura (6), es decir, circuito de Thevenin con resistencia de carga. Este es el circuito equivalente de Thevenin .

PASO 6.

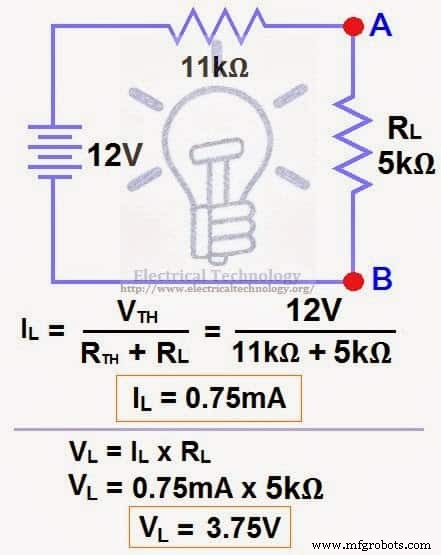
Ahora aplique el último paso, es decir, la ley de Ohm. Calcule la corriente de carga total y el voltaje de carga como se muestra en la figura 6.

I_L =V_TH / (D_TH + D_I )

Yo_L =12V / (11kΩ + 5kΩ) → =12/16kΩ

I_L =0,75 mA

Y

V_L =I_L x D_L

V_L =0,75 mA x 5 kΩ

V_L =3,75 V

Ahora compare este circuito simple con el circuito original que se muestra en la figura 1. ¿Ve cuánto más fácil será medir y calcular la corriente de carga en un circuito y una red complejos para diferentes resistencias de carga por Teorema de Thevenin ? Sí y sólo sí.

Es bueno saberlo: Tanto los teoremas de Thevenin como los de Norton se pueden aplicar a circuitos de CA y CC que contengan componentes diferenciales como resistencias, inductores y condensadores, etc. Tenga en cuenta que el voltaje de Thevenin "V_TH ” en el circuito de CA se expresa en número complejo (forma polar), mientras que la resistencia de Thevenin “R_TH ” se expresa en forma rectangular.

Publicaciones relacionadas:

• Teorema de transferencia de potencia máxima para circuitos de CA y CC
• Ley de corriente y voltaje de Kirchhoff (KCL y KVL) | Ejemplo resuelto
• Teorema de compensación:prueba, explicación y ejemplos resueltos
• Teorema de sustitución:guía paso a paso con ejemplo resuelto
• Teorema de Millman:análisis de circuitos de CA y CC:ejemplos
• Teorema de superposición:análisis de circuito con ejemplo resuelto
• Teorema de Tellegen:ejemplos resueltos y simulación de MATLAB
• Análisis del circuito del SUPERNODO | Paso a paso con ejemplo resuelto
• Análisis de circuitos SUPERMESH | Paso a paso con ejemplo resuelto
• Regla del divisor de voltaje (VDR):ejemplos resueltos para circuitos R, L y C
• Regla del divisor de corriente (CDR):ejemplos resueltos para circuitos de CA y CC
• Conversión de estrella a delta y delta a estrella. Transformación Y-Δ