Conversiones Δ-Y e Y-Δ

En muchas aplicaciones de circuitos, encontramos componentes conectados entre sí de dos maneras para formar una red de tres terminales:la configuración "Delta" o Δ (también conocida como "Pi" o π) y la configuración "Y" ( también conocida como la configuración "T").

Es posible calcular los valores adecuados de resistencias necesarios para formar un tipo de red (Δ o Y) que se comporta de manera idéntica al otro tipo, como se analiza solo a partir de las conexiones de los terminales. Es decir, si tuviéramos dos redes de resistencias separadas, una Δ y una Y, cada una con sus resistencias ocultas a la vista, con nada más que las tres terminales (A, B y C) expuestas para prueba, las resistencias podrían dimensionarse para el dos redes para que no hubiera forma de determinar eléctricamente una red aparte de la otra. En otras palabras, las redes Δ e Y equivalentes se comportan de manera idéntica.

Ecuaciones de conversión Δ e Y

Hay varias ecuaciones que se utilizan para convertir una red en otra:

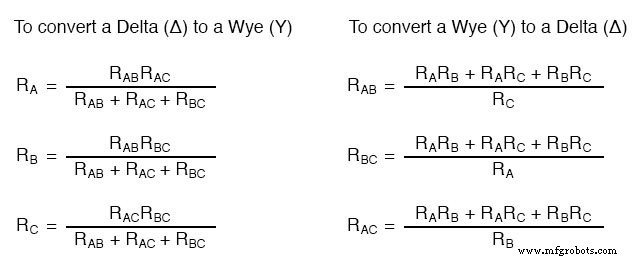
Las redes Δ e Y se ven con frecuencia en los sistemas de alimentación de CA trifásicos (un tema que se trata en el volumen II de esta serie de libros), pero incluso entonces suelen ser redes equilibradas (todas las resistencias tienen el mismo valor) y conversión de una a otra. No es necesario que implique cálculos tan complejos. ¿Cuándo necesitaría el técnico medio utilizar estas ecuaciones?

Aplicación de conversión Δ e Y

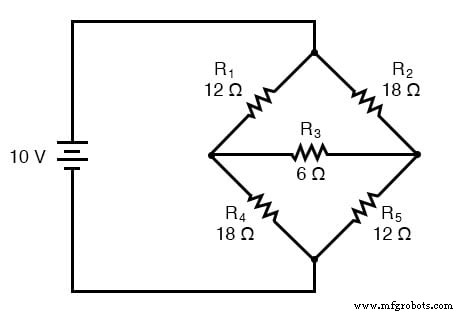
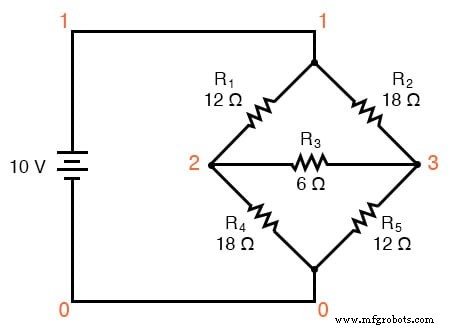
Una aplicación principal para la conversión Δ-Y es la solución de circuitos de puente desequilibrados, como el que se muestra a continuación:

La solución de este circuito con el análisis de la corriente de derivación o la corriente de malla es bastante complicada, y ni los teoremas de Millman ni de superposición son de ayuda, ya que solo hay una fuente de energía. Podríamos usar el teorema de Thevenin o Norton, tratando R ₃ como nuestra carga, pero ¿qué divertido sería eso?

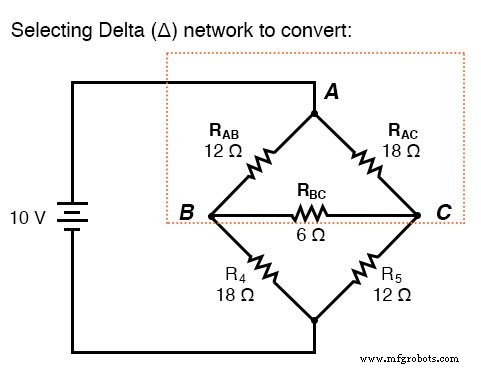
Si tuviéramos que tratar las resistencias R ₁ , R ₂ y R ₃ como si estuviera conectado en una configuración Δ (R _ab , R _ac y R _bc , respectivamente) y generar una red Y equivalente para reemplazarlos, podríamos convertir este circuito puente en un circuito de combinación en serie / paralelo (más simple):

Después de la conversión Δ-Y. . .

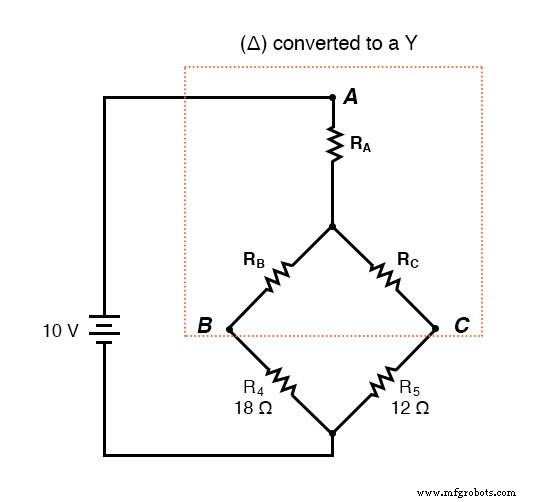
Si realizamos nuestros cálculos correctamente, los voltajes entre los puntos A, B y C serán los mismos en el circuito convertido que en el circuito original, y podemos transferir esos valores a la configuración original del puente.

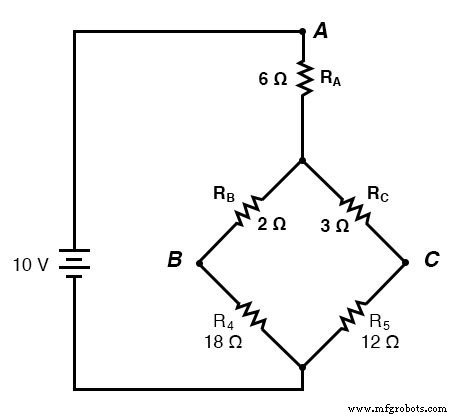
Resistencias R ₄ y R ₅ , por supuesto, siguen siendo los mismos en 18 Ω y 12 Ω, respectivamente. Analizando el circuito ahora como una combinación en serie / paralelo, llegamos a las siguientes cifras:

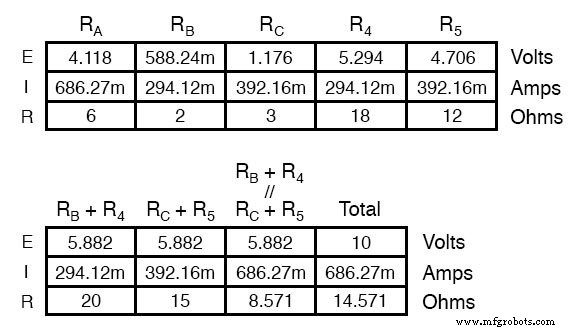
Debemos utilizar las cifras de caídas de tensión de la tabla anterior para determinar las tensiones entre los puntos A, B y C, viendo cómo se suman (o restan, como es el caso de la tensión entre los puntos B y C):

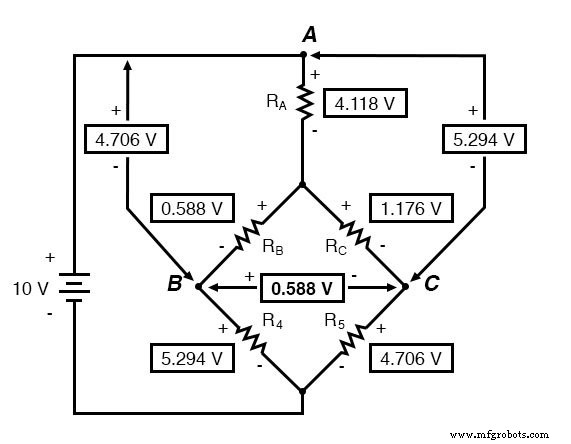
Ahora que conocemos estos voltajes, podemos transferirlos a los mismos puntos A, B y C en el circuito de puente original:

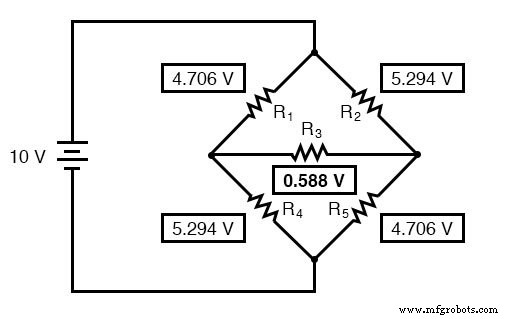
Caídas de voltaje en R ₄ y R ₅ , por supuesto, son exactamente los mismos que estaban en el circuito del convertidor.

En este punto, podríamos tomar estos voltajes y determinar las corrientes de resistencia mediante el uso repetido de la ley de Ohm (I =E / R):

Simulación con SPICE

Una rápida simulación con SPICE servirá para verificar nuestro trabajo:

 circuito puente no balanceado v1 1 0 r1 1 2 12 r2 1 3 18 r3 2 3 6 r4 2 0 18 r5 3 0 12 .dc v1 10 10 1 .impresión dc v (1,2) v (1,3) v (2,3) v (2,0) v (3,0) .fin v1 v (1,2) v (1,3) v (2,3) v (2) v (3) 1.000E + 01 4.706E + 00 5.294E + 00 5.882E-01 5.294E + 00 4.706E + 00 

Las cifras de voltaje, leídas de izquierda a derecha, representan caídas de voltaje en las cinco resistencias respectivas, R ₁ hasta R ₅ . También podría haber mostrado corrientes, pero dado que eso habría requerido la inserción de fuentes de voltaje "ficticias" en la lista de redes SPICE, y dado que estamos interesados ​​principalmente en validar las ecuaciones de conversión Δ-Y y no la Ley de Ohm, esto será suficiente.

REVISAR:

• Las redes "Delta" (Δ) también se conocen como redes "Pi" (π).
• Las redes "Y" también se conocen como redes "T".
• Las redes Δ e Y se pueden convertir en sus contrapartes equivalentes con las ecuaciones de resistencia adecuadas. Por "equivalente" me refiero a que las dos redes serán eléctricamente idénticas según se mida desde los tres terminales (A, B y C).
• Un circuito puente se puede simplificar a un circuito en serie / paralelo convirtiendo la mitad de él de una red Δ a una Y. Después de que se hayan resuelto las caídas de voltaje entre los tres puntos de conexión originales (A, B y C), esos voltajes se pueden transferir de nuevo al circuito de puente original, a través de esos mismos puntos equivalentes.

HOJA DE TRABAJO RELACIONADA:

• Hoja de trabajo de circuitos trifásicos en estrella y en triángulo