Máquinas de estados finitos

Hasta ahora, cada circuito presentado era una combinatoria circuito. Eso significa que su salida depende solo de sus entradas actuales. Las entradas anteriores para ese tipo de circuitos no tienen ningún efecto en la salida.

Sin embargo, hay muchas aplicaciones donde existe la necesidad de que nuestros circuitos tengan “memoria”; para recordar entradas anteriores y calcular sus salidas de acuerdo con ellas. Un circuito cuya salida depende no solo de la entrada actual sino también del historial de la entrada se denomina circuito secuencial .

En esta sección aprenderemos a diseñar y construir tales circuitos secuenciales. Para ver cómo funciona este procedimiento, usaremos un ejemplo, sobre el cual estudiaremos nuestro tema.

Así que supongamos que tenemos un juego de preguntas digital que funciona en un reloj y lee una entrada de un botón manual. Sin embargo, queremos que el interruptor transmita solo un pulso ALTO al circuito. Si enganchamos el botón directamente en el circuito del juego, transmitirá ALTO durante la menor cantidad de ciclos de reloj que nuestro dedo pueda lograr. En una frecuencia de reloj común, nuestro dedo nunca puede ser lo suficientemente rápido.

El procedimiento de diseño tiene pasos específicos que se deben seguir para realizar el trabajo:

Paso 1

El primer paso del procedimiento de diseño es definir con palabras simples pero claras lo que queremos que haga nuestro circuito:

“Nuestra misión es diseñar un circuito secundario que transmita un pulso ALTO con una duración de solo un ciclo cuando se presione el botón manual, y no transmitirá otro pulso hasta que se presione el botón y se vuelva a presionar”.

Paso 2

El siguiente paso es diseñar un diagrama de estado.

Este es un diagrama que está hecho de círculos y flechas y describe visualmente el funcionamiento de nuestro circuito. En términos matemáticos, este diagrama que describe el funcionamiento de nuestro circuito secuencial es una máquina de estados finitos. Tenga en cuenta que esta es una máquina de estados finitos de Moore.

Su salida es una función únicamente de su estado actual, no de su entrada. Eso contrasta con la Mealy Finite State Machine, donde la entrada afecta la salida. En este tutorial, solo se examinará la máquina de estados finitos de Moore.

El diagrama de estado de nuestro circuito es el siguiente:(Figura siguiente)

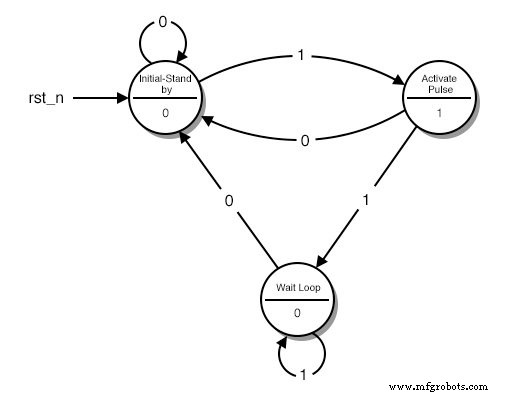
Un diagrama de estado

Cada círculo representa un "estado", una condición bien definida en la que se puede encontrar nuestra máquina. En la mitad superior del círculo describimos esa condición. La descripción nos ayuda a recordar lo que se supone que debe hacer nuestro circuito en esa condición.

• El primer círculo es la condición de "espera". Aquí es donde comienza nuestro circuito y donde espera a que se presione otro botón.
• El segundo círculo es la condición en la que se acaba de presionar el botón y nuestro circuito necesita transmitir un pulso ALTO.
• El tercer círculo es la condición en la que nuestro circuito espera a que se suelte el botón antes de que vuelva a la condición de "espera".

En la parte inferior del círculo está la salida de nuestro circuito. Si queremos que nuestro circuito transmita un ALTO en un estado específico, ponemos un 1 en ese estado. De lo contrario, ponemos un 0.

Cada flecha representa una "transición" de un estado a otro. Una transición ocurre una vez en cada ciclo de reloj. Dependiendo de la entrada actual, podemos ir a un estado diferente cada vez. Observe el número en el medio de cada flecha. Esta es la entrada actual.

Por ejemplo, cuando estamos en el estado "Inicial-Stand by" y "leemos" un 1, el diagrama nos dice que tenemos que ir al estado "Activar pulso". Si leemos un 0 debemos permanecer en el estado "Inicial-Stand by".

Entonces, ¿qué hace exactamente nuestra "Máquina"? Comienza desde el estado "Inicial - En espera" y espera hasta que se lea un 1 en la Entrada. Luego pasa al estado "Activar pulso" y transmite un pulso ALTO en su salida. Si se mantiene presionado el botón, el circuito pasa al tercer estado, el "Bucle de espera".

Allí espera hasta que se suelta el botón (la entrada pasa a 0) mientras transmite un BAJO en la salida. ¡Entonces todo ha terminado de nuevo!

Esta es posiblemente la parte más difícil del procedimiento de diseño, porque no se puede describir con pasos simples. Se necesita experiencia y un poco de pensamiento agudo para configurar un diagrama de estado, pero el resto es solo un conjunto de pasos predeterminados.

Paso 3

A continuación, reemplazamos las palabras que describen los diferentes estados del diagrama con binario números. Comenzamos la enumeración desde 0 que se asigna en el estado inicial. Luego continuamos la enumeración con cualquier estado que nos guste, hasta que todos los estados tengan su número. El resultado se parece a esto:(Figura siguiente)

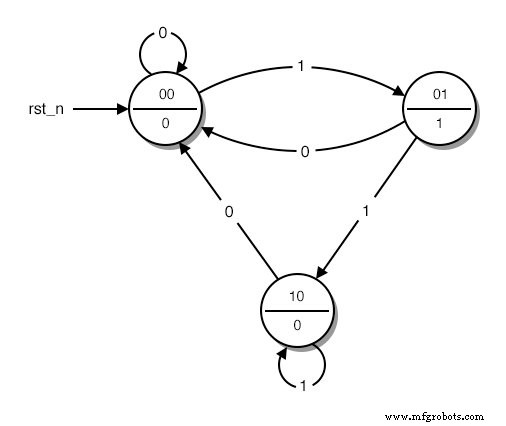
Un diagrama de estado con estados codificados

Paso 4

Luego, llenamos la Tabla de estado . Esta tabla tiene una forma muy específica. Daré la tabla de nuestro ejemplo y la usaré para explicar cómo completarla. (Figura siguiente)

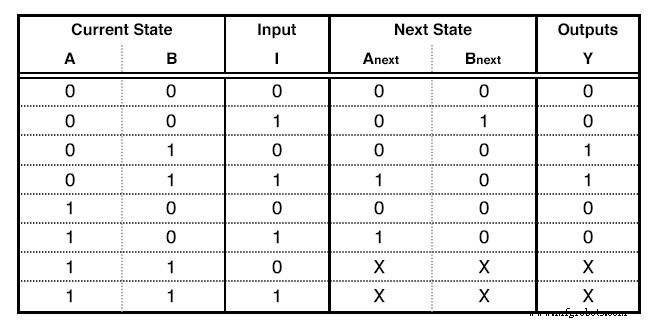
Una tabla de estado

Las primeras columnas son tantos como los bits del número más alto que le asignamos al diagrama de estado. Si tuviéramos 5 estados, habríamos usado hasta el número 100, lo que significa que usaríamos 3 columnas. Para nuestro ejemplo, usamos hasta el número 10, por lo que solo se necesitarán 2 columnas. Estas columnas describen el Estado actual de nuestro circuito.

A la derecha de las columnas Estado actual escribimos las Columnas de entrada . Estas serán tantas como nuestras variables de entrada. Nuestro ejemplo tiene solo una entrada.

A continuación, escribimos las siguientes columnas de estado . Estos son tantos como las columnas Estado actual.

Finalmente, escribimos las Columnas de salida . Estos son tantos como nuestros productos. Nuestro ejemplo tiene solo una salida. Dado que hemos construido una máquina de estados más finitos, la salida depende solo de los estados de entrada actuales. Esta es la razón por la que la columna de salidas tiene dos 1:para dar como resultado una función booleana de salida que es independiente de la entrada I. Siga leyendo para obtener más detalles. Las columnas Estado actual y Entrada son las entradas de nuestra tabla. Los completamos con todos los números binarios del 0 al:

2 ^{(Número de columnas de estado actual + Número de columnas de entrada)} -1

Afortunadamente, es más simple de lo que parece. Por lo general, habrá más filas que los estados reales que hemos creado en el diagrama de estado, pero está bien.

Cada fila de las columnas Next State se rellena de la siguiente manera:La rellenamos con el estado al que llegamos cuando, en el State Diagram, desde el Current State de la misma fila seguimos la Input de la misma fila. Si tiene que completar una fila cuyo número de estado actual no corresponde a ningún estado real en el diagrama de estado, la llenamos con los términos No importa (X). Después de todo, no nos importa adónde podemos ir desde un Estado que no existe. ¡No estaríamos allí en primer lugar! Nuevamente, es más simple de lo que parece.

La columna de salidas se llena con la salida del estado actual correspondiente en el diagrama de estado.

¡La tabla de estados está completa! Describe el comportamiento de nuestro circuito tan completamente como lo hace el diagrama de estado.

Paso 5a

El siguiente paso es tomar esa “Máquina” teórica e implementarla en un circuito. La mayoría de las veces, esta implementación involucra Flip Flops. Esta guía está dedicada a este tipo de implementación y describirá el procedimiento tanto para D - Flip Flops como para JK - Flip Flops. T - No se incluirán chanclas por ser demasiado similares a los dos casos anteriores. La selección del Flip Flop a utilizar es arbitraria y generalmente está determinada por factores de costo. La mejor opción es realizar ambos análisis y decidir qué tipo de Flip Flop da como resultado un número mínimo de puertas lógicas y un costo menor.

Primero examinaremos cómo implementamos nuestra "Máquina" con D-Flip Flops.

Necesitaremos tantos D - Flip Flops como columnas de estado, 2 en nuestro ejemplo. Por cada Flip Flop, agregaremos una columna más en nuestra tabla de estado (Figura siguiente) con el nombre de la entrada del Flip Flop, "D" para este caso. La columna que corresponde a cada Flip Flop describe qué entrada debemos darle al Flip Flop para pasar del Estado Actual al Estado Siguiente . Para el D - Flip Flop esto es fácil:la entrada necesaria es igual al siguiente estado. En las filas que contienen X, también completamos X en esta columna.

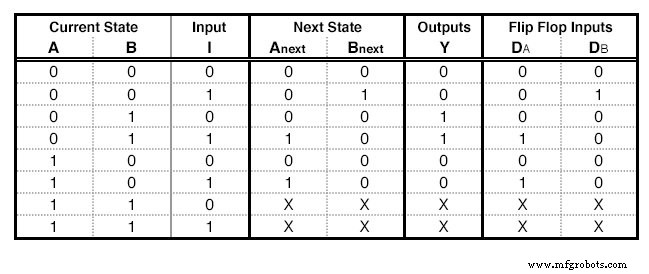
Una tabla de estado con D:excitaciones Flip Flop

Paso 5b

Podemos hacer los mismos pasos con JK - Flip Flops. Sin embargo, existen algunas diferencias. Un JK - Flip Flop tiene dos entradas, por lo tanto, necesitamos agregar dos columnas para cada Flip Flop. El contenido de cada celda lo dicta la tabla de excitación de JK:

Esta tabla dice que si queremos pasar del Estado Q al Estado Q _siguiente , necesitamos usar la entrada específica para cada terminal. Por ejemplo, para pasar de 0 a 1, necesitamos alimentar a J con 1 y no nos importa qué entrada alimentamos a la terminal K.

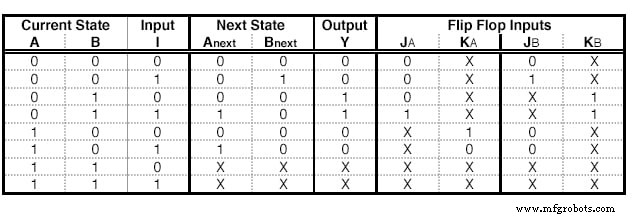
Una tabla de estado con JK - Emociones Flip Flop

Paso 6

Estamos en la etapa final de nuestro procedimiento. Lo que queda es determinar las funciones booleanas que producen las entradas de nuestros Flip Flops y la Salida. Extraeremos una función booleana por cada entrada de Flip Flop que tengamos. Esto se puede hacer con un mapa de Karnaugh. Las variables de entrada de este mapa son las variables de estado actual así como las Entradas.

Dicho esto, las funciones de entrada para nuestras D - Flip Flops son las siguientes:(Figura siguiente)

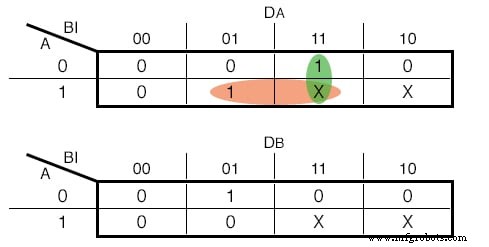
Mapas de Karnaugh para D - Entradas Flip Flop

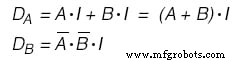
Si elegimos usar JK - Flip Flops, nuestras funciones serían las siguientes:(Figura siguiente)

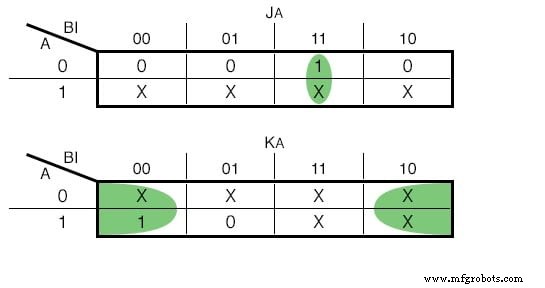
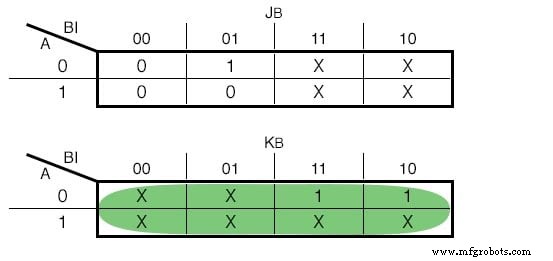
Mapa de Karnaugh para JK - Entrada Flip Flop

También se utilizará un mapa de Karnaugh para determinar la función de la salida:(Figura siguiente)

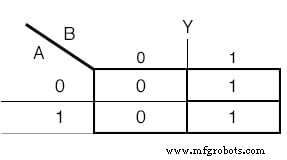
Mapa de Karnaugh para la variable de salida Y

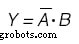
Paso 7

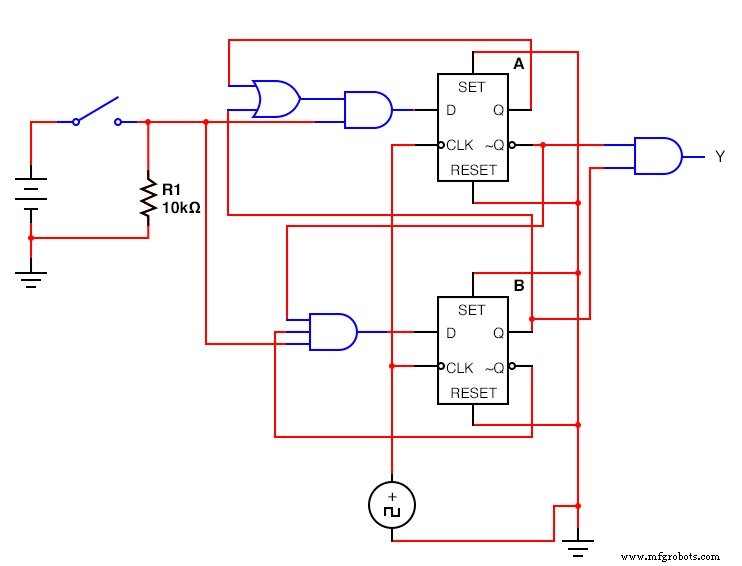
Diseñamos nuestro circuito. Colocamos las Flip Flops y usamos puertas lógicas para formar las funciones booleanas que calculamos. Las puertas toman la entrada de la salida de los Flip Flops y la entrada del circuito. ¡No olvides conectar el reloj a las Flip Flops!

La versión D - Flip Flop:(Figura siguiente)

El circuito secuencial D - Flip Flop completado

La versión JK - Flip Flop:(Figura siguiente)

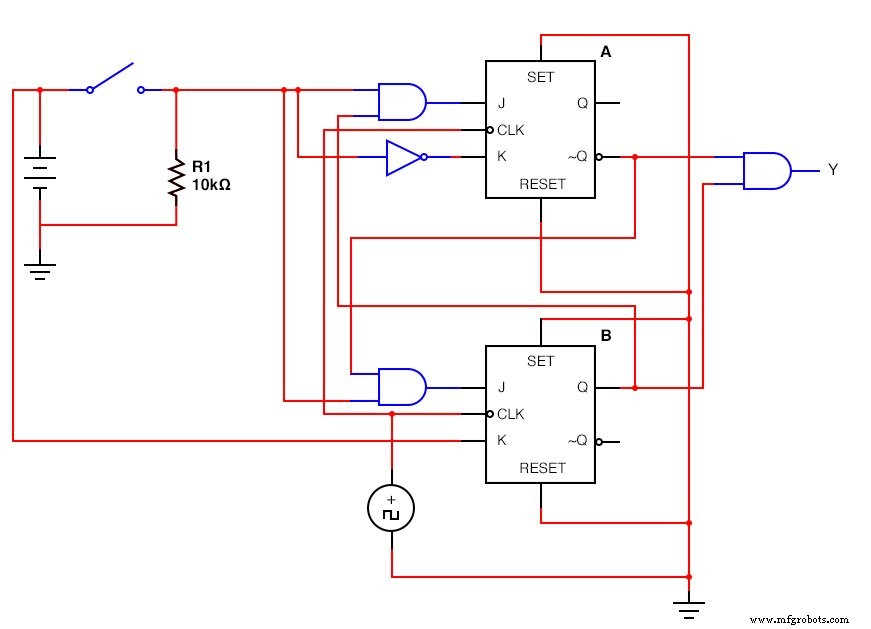
El circuito secuencial JK - Flip Flop completado

¡Eso es todo! Hemos diseñado y construido con éxito un circuito secuencial. Al principio puede parecer una tarea abrumadora, pero después de la práctica y la repetición, el procedimiento se volverá trivial. Los circuitos secuenciales pueden ser útiles como partes de control de circuitos más grandes y pueden realizar cualquier tarea lógica secuencial que podamos imaginar. ¡El cielo es el limite! (o la placa de circuito, al menos)

REVISAR:

• Una función de lógica secuencial tiene una función de "memoria" y tiene en cuenta las entradas pasadas para decidir la salida.
• La máquina de estados finitos es un modelo matemático abstracto de una función lógica secuencial. Tiene entradas, salidas y número de estados finitos.
• Los FSM se implementan en circuitos de la vida real mediante el uso de Flip Flops
• El procedimiento de implementación necesita un orden específico de pasos (algoritmo), para poder llevarse a cabo.