Caracterización a escala atómica de la deformación por deslizamiento y maquinabilidad nanométrica del monocristal 6H-SiC
Resumen
Como importante material semiconductor de tercera generación, el mecanismo de microdeformación y eliminación de 6H-SiC a escala atómica son vitales para obtener una superficie ultrasuave y sin daños con pasos atómicos. Debido a las dificultades para observar directamente la superficie / subsuelo de la región de nanomáquinas con los medios experimentales actuales, el método de dinámica molecular se utiliza para estudiar los detalles a escala atómica en el proceso de nanomáquinas, como el movimiento de deslizamiento de dislocación, la transición de fase y el mecanismo de separación de materiales. Se investiga enfáticamente la influencia de la anisotropía inducida por cristalografía sobre la deformación por deslizamiento y la maquinabilidad nanométrica del 6H-SiC. Este estudio contribuye significativamente a la comprensión del proceso de microdeformación y nanomáquina de 6H-SiC.
Introducción
Como material semiconductor de tercera generación con banda prohibida amplia, el SiC tiene las características de alto campo de ruptura, alta tolerancia a la radiación, alta velocidad de saturación del portador, conductividad térmica rápida, pequeña constante dieléctrica y propiedades químicas estables, por lo que tiene amplias aplicaciones en los campos. de dispositivos optoelectrónicos de alta temperatura, alta frecuencia, alta potencia, antirradiación y de longitud de onda corta e integración optoelectrónica [1].
Los cristales de SiC más utilizados son 3C, 4H y 6H. Los métodos de procesamiento como el esmerilado / lapeado / pulido siguen siendo los principales métodos durante el mecanizado de SiC monocristalino. Sin embargo, la relación de dureza entre el diamante y el SiC es cercana a 2:1 (la profundidad de procesamiento <50 nm)), que es mucho más baja que el valor recomendado de 5:1 para el proceso de mecanizado [2]. El desgaste severo de la herramienta de corte y el daño del subsuelo influyen directamente en la calidad de la oblea. Para abordar estos problemas, se ha realizado una gran cantidad de trabajo para comprender el comportamiento de eliminación de SiC a nanoescala. El mecanismo de eliminación de 3C-SiC y la influencia de los factores de procesamiento se han estudiado a fondo, como el mecanismo de deformación plástica durante el proceso de corte [3,4,5,6,7], el desgaste de la herramienta [8], el comportamiento de fricción [9 ], y anisotropía de 3C-SiC [10] e influencia de las temperaturas de corte [11].
6H-SiC tiene una estructura de pila ABCACB más compleja. Aunque se estudia el mecanismo de eliminación de 6H-SiC en el procesamiento SPDT (torneado de diamante de un solo punto) (como la influencia del ángulo de inclinación de la herramienta en el proceso de eliminación de material [12] y la transición frágil-dúctil [13]), la investigación es obviamente menos de 3C-SiC. La banda prohibida de 6H-SiC (3 eV) es obviamente más alta que la de 3C-SiC (2,3 eV). En la actualidad, el nivel tecnológico del proceso de crecimiento de las barras de 6H-SiC es mucho más alto que el del 3C-SiC. El 6H-SiC se utiliza mucho más en aplicaciones industriales que el 3C-SiC. Los dispositivos correspondientes se han aplicado en campos de alta frecuencia, alta potencia y alta temperatura, como el rectificador Schottky, el tiratrón y el MOSFET de potencia (Transistor de efecto de campo de semiconductor de óxido metálico). Para mejorar la calidad de la superficie / subsuperficie mecanizada del 6H-SiC, el medio más eficiente y efectivo en la actualidad es encontrar una combinación adecuada de plano de cristal (superficie de mecanizado) / orientación del cristal (dirección de mecanizado) que sea más adecuada para el proceso de 6H -SiC.
Los experimentos de scratch y las simulaciones son algunos de los métodos más comunes y efectivos para explorar el comportamiento de eliminación [14, 15]. La investigación sobre el mecanismo de eliminación de material durante el proceso de rayado tiene una gran importancia orientadora para el proceso de mecanizado abrasivo real. El método de dinámica molecular puede proporcionar un proceso de formación y eliminación de daños a nanoescala. Por lo tanto, se utilizó la simulación de rayado de dinámica molecular para analizar el comportamiento de eliminación de 6H-SiC bajo la influencia de la anisotropía inducida por cristalografía.
Metodología
Las simulaciones de corte en este documento se completaron utilizando un simulador masivamente paralelo atómico / molecular a gran escala (LAMMPS) [16]. En este estudio se utilizaron OIVTO [17] y el método de identificación de estructura de diamante [18] para la visualización del modelo y la identificación de defectos. Las implementaciones del modelado de piezas y herramientas dependían de LAMMPS sin la ayuda de otro software. Como se muestra en la Fig. 1a-c, tanto la pieza de trabajo como la herramienta se establecieron como cuerpos deformables, y el comportamiento de desgaste se investigó durante la simulación. La herramienta y el modelo de la pieza de trabajo se dividieron en tres partes:una capa atómica límite, una capa atómica termostática y una zona de átomos newtonianos. Para mantener la pieza de trabajo en la posición inicial, se fijaron los átomos de la capa límite en el extremo inferior y derecho de la pieza de trabajo. Los átomos en la capa del termostato y la capa newtoniana siguen la segunda ley de Newton. Se aplicó un límite periódico a lo largo de y dirección. Antes de la simulación de rayado, los modelos se relajaron mediante el conjunto NVE con el método de termostato Berendsen. Se aplicó un período de relajación de 50 ps antes de las simulaciones de rayado para obtener un estado de energía estable. La forma abrasiva es una pirámide triangular de corona esférica con un ángulo de borde a borde de 90 °. Como se muestra en la Fig. 2, los planos cristalinos comunes (plano a (plano basal), plano m (plano prismático) y plano c) para 6H-SiC se seleccionaron como superficies de mecanizado. Teniendo en cuenta la simetría de la estructura, se seleccionaron las siguientes combinaciones de plano / orientación como superficie de mecanizado / dirección de mecanizado:\ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline { 1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \). Los parámetros de procesamiento de la simulación se muestran en la Tabla 1. Antes de la simulación de rayado, los abrasivos se colocaron en el lado izquierdo de la pieza de trabajo y la punta del abrasivo está 50 Å por debajo de la superficie superior de la pieza de trabajo. La distancia más cercana entre los abrasivos y la pieza de trabajo es de 30 Å, que está lejos del rango de corte del potencial de interacción. El abrasivo se mueve desde el extremo libre de la pieza de trabajo en la dirección positiva de x -eje y complete el proceso de rayado.
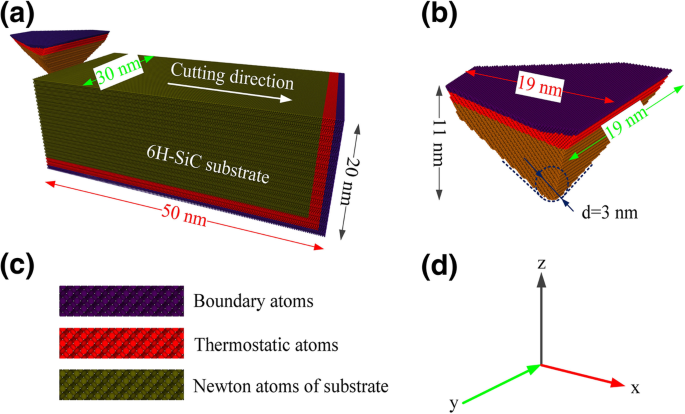
un Modelo MD de simulación de nano-rayado. b La morfología de la herramienta. c Estructura del modelo. d Dirección del eje
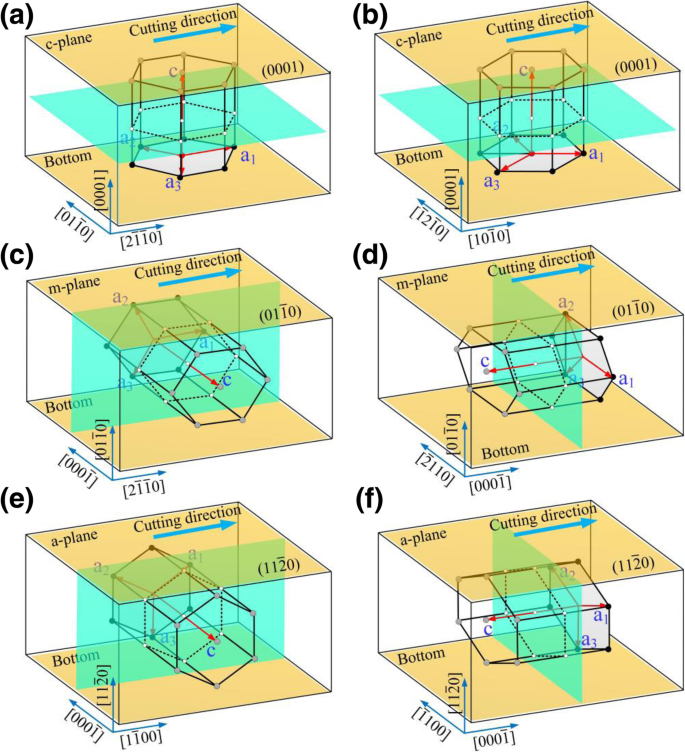
Diagrama esquemático del proceso de rayado, donde a - f son los modos de proceso correspondientes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente
La función de potencial atómico juega un papel crucial en la precisión y confiabilidad de la simulación de dinámica molecular. Según las pruebas y simulaciones anteriores para las propiedades mecánicas y los mecanismos de eliminación del SiC monocristalino, la función de potencial de orden de enlace analítico (ABOP) propuesta por Erhart y Albe [19] es más adecuada para interacciones de silicio y carbono. Los parámetros utilizados en la función potencial se muestran en la Tabla 2 [19]. En lugar de la función de energía potencial de Tersoff [6], la función de potencial ABOP se utiliza para definir las interacciones Si-Si, CC y Si-C en y entre la herramienta y la pieza de trabajo durante el procesamiento [2, 7, 8, 10, 11].
Resultados y discusión
Análisis de maquinabilidad nanométrica
Como se muestra en las Figs. 3 y 4, la anisotropía de 6H-SiC tuvo un impacto significativo en la maquinabilidad nanométrica (profundidad mecanizada, modo de remoción, cantidad de remoción y profundidad de daño subsuperficial (SSD), etc.). Según la relación entre la superficie de mecanizado / dirección de mecanizado y el plano basal / c eje (ver Fig.3), los modos de procesamiento del material se pueden dividir en tres categorías:(i) el plano basal se selecciona como la superficie de mecanizado, (ii) el plano basal es perpendicular a la superficie de mecanizado y c -eje es perpendicular a la dirección de mecanizado, y (iii) el c -Eje es paralelo a la dirección de mecanizado.
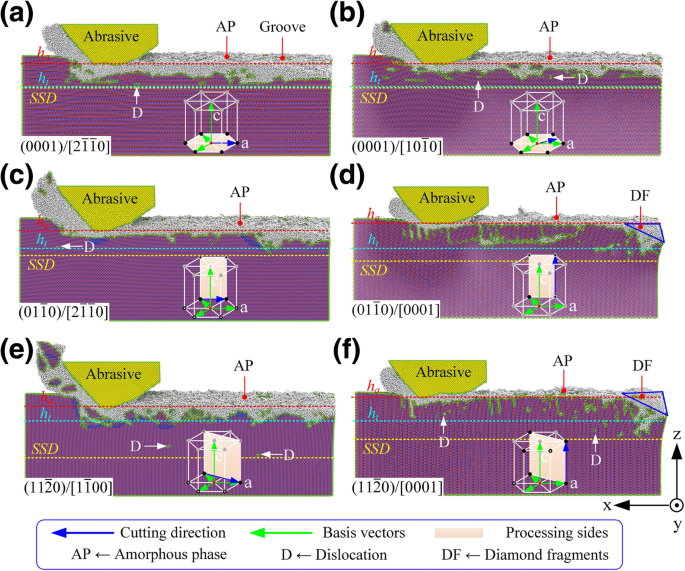
Topografía de la superficie mecanizada en diferentes condiciones de orientación / plano de cristal, donde a - f son los modos de proceso correspondientes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente
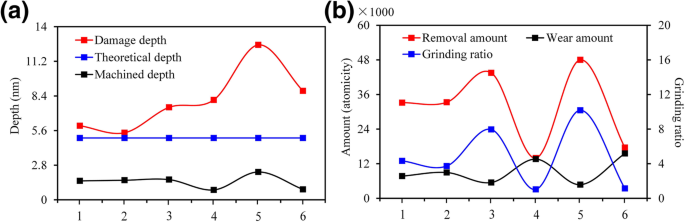
Maquinabilidad nanométrica en diferentes condiciones de orientación / plano de cristal, a la influencia de la anisotropía en la profundidad mecanizada y la profundidad del daño, b la influencia de la anisotropía en la cantidad de remoción, la cantidad de desgaste y la relación de molienda. 1, 2, 3, 4, 5 y 6 son los métodos de proceso correspondientes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente. La profundidad de la capa de daño se refiere a la profundidad máxima de los defectos internos del cristal causados por el rayado. La profundidad teórica se refiere a la profundidad preestablecida antes del procesamiento. La profundidad mecanizada se refiere a la profundidad residual después del rayado. La cantidad de remoción se refiere al número de átomos de los que se extrae el material de la pieza de trabajo. La cantidad de desgaste se refiere a la diferencia en el número de átomos de los granos abrasivos antes y después del rayado
(i) Como se muestra en la Fig. 3a, b, la maquinabilidad nanométrica de 6H-SiC fue extremadamente similar cuando el modo de procesamiento se seleccionó como \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) y \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). Sin embargo, el proceso de eliminación de 6H-SiC se inclinó más hacia el modo frágil cuando el modo de procesamiento se seleccionó como \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). (ii) Como se muestra en la Fig. 3c, e, cuando los modos de procesamiento se seleccionaron como \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), la profundidad mecanizada y la cantidad de remoción de material fueron significativamente mayores que las en los otros métodos de procesamiento. Como se muestra en la Fig.4, bajo la misma profundidad de procesamiento teórica ( h t =5.0 nm), la tasa de remoción de material en el modo de procesamiento \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) fue 3.4 veces mayor que que en el modo de procesamiento \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \). La relación de procesamiento de material (cantidad de material extraído / desgaste de la herramienta) fue de 10.1, pero el SSD bajo este parámetro de procesamiento también fue mucho más alto que en otras condiciones de procesamiento, alcanzando 2.3 veces \ ((0001) / \ left [10 \ overline { 1} 0 \ derecha] \). Había una gran cantidad de nanocristalitos en las superficies mecanizadas y en las virutas. En esta condición se produjo un gran número de fallas frágiles. El modo de procesamiento \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) solo es adecuado para el procesamiento de nanogroove que requiere una alta eficiencia de procesamiento pero es insensible a la Daños subsuperficiales. La tasa de eliminación de material de \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) fue similar a la de \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) pero el SSD era solo el 50% de este último. Además, el grosor de la capa amorfa en la superficie mecanizada era mucho menor que el de \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) y \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). La distribución de la fase subterránea fue uniforme y las propiedades mecánicas de toda la ranura fueron mejores que las de los otros métodos de procesamiento. Por lo tanto, el modo de procesamiento \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) es la mejor opción para el procesamiento de micro-nano surcos en una superficie de 6H-SiC con alta eficiencia , alta precisión y SSD bajo. (iii) Como se muestra en las Figs. 3d, f, cuando la dirección de mecanizado era paralela a c eje, la punta estaba muy desgastada durante la etapa de procesamiento inicial. Aunque la profundidad de mecanizado y la tasa de eliminación de material fueron mucho más bajas que las de los otros métodos de procesamiento y la proporción de procesamiento de material fue de solo 1,0, el SSD de \ (\ left (01 \ overline {1} 0 \ right) / \ left [ 0001 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) los modos de procesamiento eran más que los de \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \). Por lo tanto, no se recomienda emplear \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) en el procesamiento de micro-nano surcos en la superficie de 6H-SiC. Sin embargo, estos modos demuestran una excelente resistencia al desgaste; por lo tanto, son aptas para la cara de desprendimiento de la herramienta de corte de SiC monocristalino, que tiene amplias perspectivas en el campo del procesamiento de ultraprecisión de metales ferrosos.
Análisis del movimiento de los labios y la distribución del daño del subsuelo
Distribución de factores de Schmid en el proceso de raspado basado en la punta de una pirámide triangular
Los sistemas de deslizamiento comunes del sistema de cristal hexagonal (ver Fig. 4) incluyen principalmente deslizamiento basal, deslizamiento prismático y deslizamiento piramidal. La resistencia al deslizamiento está relacionada con la energía de falla de apilamiento generalizada (GSF) y d E GSF / d x frente a ( x / b ) de los sistemas de deslizamiento. El movimiento de deslizamiento se produciría en el plano más denso ya lo largo de la dirección más corta [10]. Los sistemas de deslizamiento preferenciales en el deslizamiento basal son deslizamiento basal (conjuntos aleatorios) / <\ (1 \ overline {1} 00 \)> y deslizamiento basal (conjuntos aleatorios) / <\ (11 \ overline {2} 0 \)> [20]. Como el primero carece de un mínimo de energía intermedio, el segundo tiene prioridad en las simulaciones y experimentos [20]. Por lo tanto, los movimientos de deslizamiento considerados en este trabajo son los siguientes:deslizamiento basal (conjuntos aleatorios) / <\ (11 \ overline {2} 0 \)> y deslizamiento prismático y deslizamiento
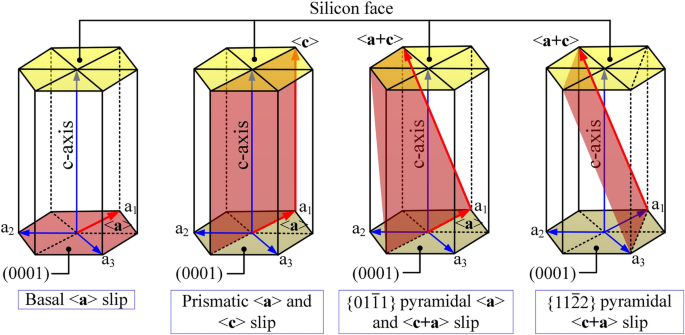
Sistemas de deslizamiento de sistema hexagonal
El componente de esfuerzo cortante en el plano de deslizamiento τ ss se puede calcular mediante la relación:
$$ {\ tau} _ {\ mathrm {ss}} ={\ sigma} _ {\ mathrm {cont}} \ mathit {\ cos} <\ overset {\ rightharpoonup} {f}, \ overset {\ rightharpoonup} {n_g}> \ cos <\ overset {\ rightharpoonup} {f}, \ overset {\ rightharpoonup} {t_g}> ={\ sigma} _ {\ mathrm {cont}} \ bullet m $$ (1)donde σ cont es el estrés de contacto, \ (\ overset {\ rightharpoonup} {f} \) es la dirección de carga, \ (\ overset {\ rightharpoonup} {n_g} \) y \ (\ overset {\ rightharpoonup} {t_g} \) son el plano de deslizamiento normal y la dirección de deslizamiento en el sistema de coordenadas cartesianas global, y m es el factor de Schmid. El sistema de coordenadas global fue fijo y el sistema de coordenadas local rotó con la dirección del cristal. La x -eje del sistema de coordenadas local era paralelo al vector básico \ (\ overset {\ rightharpoonup} {a_1} \) mientras que z -eje era paralelo al vector básico \ (\ overset {\ rightharpoonup} {c} \).
Durante el proceso de rayado, la cara de contacto principal de la punta de la pirámide triangular era la cara de inclinación, pero cuando la herramienta se desgastaba mucho, la cara de contacto principal pasaba al compuesto de la cara de inclinación y la punta. La dirección de carga correspondiente \ (\ overset {\ rightharpoonup} {f} \) se presenta como
$$ \ left \ {\ begin {array} {c} \ overset {\ rightharpoonup} {f_1} =\ left ({f} _ {1x}, {f} _ {1y}, {f} _ {1z} \ right) \ kern8em \ mathrm {rastrillo} \ \ mathrm {face} \ \\ {} \ overset {\ rightharpoonup} {f_2} =\ left ({f} _ {2x}, {f} _ {2y}, {f} _ {2z} \ right) \ kern9.75em \ mathrm {tip} \ \ mathrm {top} \ end {array} \ right. $$ (2)donde \ (\ overset {\ rightharpoonup} {f_1} =\ left (1,0, - \ sqrt {2} \ right) \), \ (\ overset {\ rightharpoonup} {f_2} =\ left (0,0 , -1 \ right) \) en el sistema de coordenadas global.
Como sistema de cristal hexagonal, el sistema de deslizamiento de 6H-SiC se puede expresar como { h k i l } / < u v t w >. El plano de deslizamiento normal \ (\ overset {\ rightharpoonup} {n_c} \) y la dirección de deslizamiento \ (\ overset {\ rightharpoonup} {t_c} \) en el sistema de coordenadas cartesianas local se muestran como
$$ \ overset {\ rightharpoonup} {n_c} =\ left (\ frac {3} {2} h, \ frac {\ sqrt {3}} {2} \ left (h + 2k \ right), \ frac { 3 la} {2c} \ right) $$ (3) $$ \ overset {\ rightharpoonup} {t_c} =\ left (u- \ frac {1} {2} \ left (v + t \ right), \ frac {\ sqrt {3}} {2} \ left (vt \ right), \ frac {c} {a} w \ right) $$ (4)El plano de deslizamiento normal \ (\ overset {\ rightharpoonup} {n_g} \) y la dirección de deslizamiento \ (\ overset {\ rightharpoonup} {t_g} \) en el sistema de coordenadas cartesianas global se muestran como
$$ \ overset {\ rightharpoonup} {n_g} =T \ bullet \ overset {\ rightharpoonup} {n_c} $$ (4) $$ \ overset {\ rightharpoonup} {t_g} =T \ overset {\ rightharpoonup} {\ viñeta {t} _c} $$ (5)donde la forma de la matriz de rotación desde el sistema de coordenadas global al sistema de coordenadas local y los ángulos de rotación correspondientes se muestran en la Tabla 3
Según las fórmulas (1) - (5), los factores de Schmid de los sistemas de deslizamiento correspondientes cuando las direcciones de carga eran \ (\ overset {\ rightharpoonup} {f_1} \) y \ (\ overset {\ rightharpoonup} {f_2} \ ) se muestran en la Tabla 4. (i) El valor c / a de 6H-SiC alcanzó 4,901, que es mucho mayor que 1,633. Por lo tanto, el esfuerzo cortante crítico requerido para el deslizamiento basal fue menor que el del sistema de deslizamiento prismático. Cuando la superficie mecanizada era un plano basal, el coeficiente del sistema de deslizamiento basal era más alto que el de los otros sistemas de deslizamiento. Por lo tanto, cuando los modos de procesamiento se seleccionaron como \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) y \ ((0001) / \ left [10 \ overline {1 } 0 \ right] \), el movimiento de deslizamiento basal tuvo lugar primero. (ii) Cuando los modos de procesamiento se seleccionaron como \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), considerando solo las direcciones de carga \ (\ overset {\ rightharpoonup} {f_1} \) y \ ( \ overset {\ rightharpoonup} {f_2} \), era teóricamente imposible que ocurriera el deslizamiento basal, y el movimiento de deslizamiento prismático tuvo prioridad. (iii) Cuando los modos de procesamiento se seleccionaron como \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right ) / \ left [0001 \ right] \), como se muestra en la Fig.4, la punta se desgastó seriamente durante la etapa de procesamiento inicial y \ (\ overset {\ rightharpoonup} {f_2} \) jugó un papel crucial en el proceso de rascado. Por lo tanto, el movimiento de deslizamiento ocurriría en el sistema de deslizamiento prismático distribuido simétricamente con el plano YOZ en las coordenadas globales.
Distribución de daños superficiales / subsuperficiales
Como se muestra en la Fig. 6a, b cuando \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) y \ ((0001) / \ left [01 \ overline {1 } 0 \ right] \), el movimiento de deslizamiento se produjo principalmente en el sistema de deslizamiento \ ((0001) / <1 \ overline {2} 10> \), que se debe al empuje hacia adelante de la herramienta. El modo de movimiento deslizante correspondiente es coherente con los resultados del cálculo del coeficiente de Schmidt. Había granos nanocristalinos y desviaciones de la red en el área del subsuelo y estos daños formaron algunas zonas irregulares de distorsión de la red. La fase amorfa cubrió toda la superficie mecanizada y la profundidad de la dislocación estuvo cerca de la profundidad de la capa de distorsión de celosía.
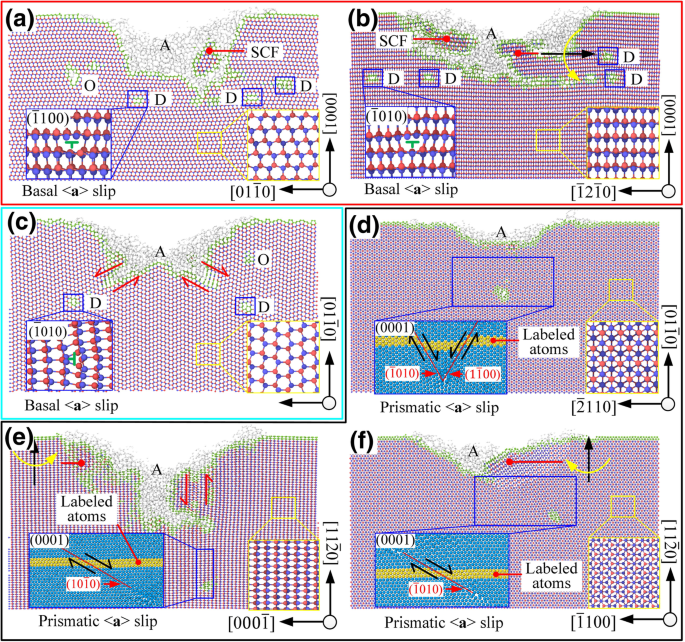
La sección transversal del área mecanizada, D es dislocación, A es una fase amorfa, SCF es una forma monocristalina, O es otro tipo de defecto, donde un - f son los modos de proceso correspondientes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) y \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente.
Cuando se selecciona \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), como el coeficiente de Schmidt de < basal un > deslizamiento es igual a 0, el basal < a > el deslizamiento no debería ocurrir en teoría. Pero el ángulo entre la dirección de carga \ (\ overset {\ rightharpoonup} {f_1} \) y la dirección de deslizamiento \ (\ left [11 \ overline {2} 0 \ right] \) era de solo 5,3 °. Bajo la acción de cizallamiento debido al movimiento relativo entre el área de contacto y el área sin contacto (ver Fig. 6c), la < a > el deslizamiento se activó antes del deslizamiento prismático en el modo de procesamiento de \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) y Ocurrió en ambos lados de la ranura en V. Bajo el modo de procesamiento de \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), los ángulos entre la dirección de carga \ (\ overset {\ rightharpoonup } {f_1} \) y las direcciones deslizantes \ (\ left [1 \ overline {2} 10 \ right] \) y \ (\ left [\ overline {1} \ overline {1} 20 \ right] \) fueron 24,7 ° y 35,3 °, respectivamente. La acción de cizallamiento no indujo un movimiento de deslizamiento del plano basal. El modo de movimiento de deslizamiento correspondiente es consistente con los resultados del cálculo del coeficiente de Schmidt. Como se muestra en la Fig. 6e, cuando se seleccionó \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), el sistema de deslizamiento \ (\ left [ 1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) tenía un coeficiente de Schmidt alto bajo la acción conjunta de \ (\ overset {\ rightharpoonup} {f_1} \) y \ (\ overset {\ rightharpoonup} {f_2} \), lo que inevitablemente daría como resultado una gran profundidad de la capa de daño del subsuelo. La distorsión de la red y la fase amorfa también existieron, pero a diferencia del mecanizado en el plano basal, la profundidad de dislocación fue significativamente mayor que la de la distorsión de la red. El sp 3 → sp 2 El comportamiento de transición ocurrió en la región del subsuelo.
Cuando la dirección de procesamiento era paralela a la c -Eje, debido al desgaste severo de la punta, el deslizamiento prismático causado por la extrusión hacia abajo fue el modo de movimiento de deslizamiento primario en la etapa estable de rayado. El modo de movimiento de deslizamiento correspondiente fue consistente con los resultados del cálculo del coeficiente de Schmidt. Cuando se seleccionó \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \), con la dirección de carga \ (\ overset {\ rightharpoonup} {f_2} \), los sistemas de deslizamiento \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) y \ (\ left [\ overline {1} \ overline {1} 20 \ right] / \ left (1 \ overline {1} 00 \ right) \) tenía el mismo coeficiente de Schmidt, se produjo un deslizamiento cruzado en las dos superficies de deslizamiento con un ángulo de 60 °, y luego, se produjo el efecto de fijación que obstaculizó el movimiento de deslizamiento . Por lo tanto, la profundidad máxima de daño subsuperficial SSD máx sería menor o igual que h t tan θ / 2 cuna α / 2, donde θ =101 ° es el ángulo teórico del nanogroove y α =60 ° es el ángulo entre el plano de deslizamiento \ (\ left (\ overline {1} 010 \ right) \) y \ (\ left (1 \ overline {1} 00 \ derecha) \). Cuando se seleccionó \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), los sistemas de deslizamiento \ (\ left [\ overline {2} 110 \ right] / \ left ( 0 \ overline {1} 10 \ right) \) y \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) también tenían el mismo coeficiente de Schmidt, pero el movimiento de deslizamiento se vio afectado por el desgaste irregular de la punta y solo se produjo el sistema de deslizamiento \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \).
En resumen, como se muestra en la Fig. 7, los daños en las regiones del subsuelo bajo diferentes condiciones de procesamiento fueron principalmente dislocaciones, distorsión de la red (torsión / deslizamiento relativo) y fase amorfa. La deformación del 6H-SiC fue causada principalmente por el movimiento de deslizamiento, la no cristalización de los materiales y la distorsión irregular de la red. Los principales modos de deformación por deslizamiento fueron el deslizamiento basal y el deslizamiento prismático, que están estrechamente relacionados con la superficie / dirección de procesamiento.
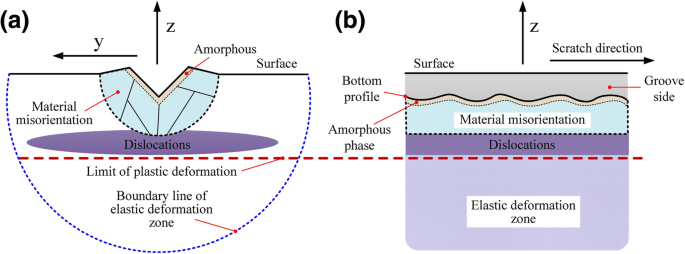
Distribución de la forma de daño superficial / subterráneo procesado. un xy sección transversal. b xz sección transversal
Comentarios finales
En este trabajo, se investigó el mecanismo de deformación y la maquinabilidad nanométrica del 6H-SiC bajo diferentes combinaciones de plano de cristal (superficie de mecanizado) / orientación del cristal (dirección de mecanizado) y se extraen las siguientes conclusiones:
- (1)
El mecanismo de deformación del 6H-SiC durante el proceso de rayado a nanoescala es principalmente el resultado de la combinación de transición de fase amorfa, distorsión de celosía y movimiento de deslizamiento de dislocación. La profundidad de la línea de dislocación determina la profundidad del daño subsuperficial en el área mecanizada de 6H-SiC.
- (2)
< a basal> deslizamiento y prismático < a > el movimiento de deslizamiento juega un papel dominante en la deformación por deslizamiento del 6H-SiC durante el proceso de rayado. Además del modo de procesamiento plano prismático / < a >, el movimiento de deslizamiento durante el proceso de rayado de 6H-SiC podría predecirse mediante el algoritmo de Schmidt.
- (3)
El modo de procesamiento \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) es propicio para lograr una alta tasa de eliminación y un bajo nivel de abrasión desgaste, que es apto para el mecanizado de la superficie 6H-SiC. El plano basal y c Los ejes son la cara y la dirección difíciles de mecanizar del 6H-SiC, que se pueden utilizar como referencia para el diseño de la herramienta de corte.
Disponibilidad de datos y materiales
Todos los datos generados o analizados durante este estudio se incluyen en este artículo.
Abreviaturas
- A :
-
Fase amorfa
- ABOP:
-
Potencial de orden de enlace analítico
- D :
-
Dislocación
- d :
-
Espesor de viruta no deformado
- GSF:
-
Energía de falla de apilamiento generalizada
- LAMMPS:
-
Simulador paralelo masivo atómico / molecular a gran escala
- MD:
-
Dinámica molecular
- MOSFET:
-
Transistor de efecto de campo semiconductor de óxido metálico
- NVE:
-
Número, volumen y energía
- O :
-
Otro tipo de defecto
- SCF:
-
Forma de monocristal
- SPDT:
-
Torneado de diamantes de un solo punto
- SSD:
-
Profundidad del daño subsuperficial
- SSD max :
-
Profundidad máxima de daño subsuperficial
Nanomateriales
- Desbarbado y desbarbado criogénico
- Fabricación y caracterización de nanoclips de ZnO mediante el proceso mediado por poliol
- Desarrollo y caracterización de compuestos de vitrocerámica que contienen Sr basados en hidroxiapatita biogénica
- Síntesis en un solo recipiente de nanopartículas de núcleo-capa de CoFe2O4 @ Ag monodispersas y su caracterización
- ¿Qué es la pulvimetalurgia? Definición y proceso
- ¿Qué es el mecanizado químico? - Trabajo y proceso
- ¿Qué es el mecanizado ultrasónico? - Trabajo y proceso
- ¿Qué es la soldadura por pulverización? - Proceso y técnicas
- Proceso de fabricación Significado y tipos
- Servicios de rectificado de superficies:proceso y precisión
- Proceso de laminación en frío y en caliente



