Propiedades de la fase geométrica en oscilaciones electromecánicas de resonadores de nanocables basados en nanotubos de carbono

Resumen

La fase geométrica es una evolución de fase adicional en la función de onda de las vibraciones que es potencialmente aplicable en una amplia gama de ciencia y tecnología. Las características de la fase geométrica en estado comprimido para un resonador de nanocables basado en nanotubos de carbono se han investigado mediante el método del operador invariante. La introducción de un operador invariante lineal, que es útil para tratar un complicado sistema hamiltoniano dependiente del tiempo, nos permitió derivar la fórmula analítica de la fase geométrica. Haciendo uso de esto, hemos analizado el comportamiento temporal de la fase geométrica a partir de ilustraciones relevantes. Se ha investigado la influencia de los parámetros de compresión en la evolución de la fase geométrica. La fase geométrica, en general, oscila y la envolvente de dicha oscilación aumenta con el tiempo. La tasa de aumento de la fase geométrica es grande cuando los parámetros, como la amplitud clásica de la oscilación, el factor de amortiguación y la amplitud de la fuerza impulsora, son grandes. Hemos confirmado un aumento muy brusco de la fase geométrica a lo largo del tiempo en el caso de que la frecuencia angular del sistema se acerque a la frecuencia angular de resonancia. Nuestro desarrollo con respecto a las características de la fase geométrica es crucial para comprender las características topológicas en las oscilaciones de nanocables.

Introducción

Las vibraciones mecánicas de los resonadores más pequeños, como los nanocables basados en nanotubos de carbono (basados en CNT) [1-3], los nanocables semiconductores [4], los grafenos [5] y las partículas levitadas [6], han sido un tema de investigación principal en la comunidad de la nanociencia durante más de una década. Se han realizado investigaciones activas sobre oscilaciones electromecánicas de resonadores de nanocables impulsados por una fuerza periódica externa, tanto en esferas teóricas como experimentales. En particular, los resonadores de nanocables basados en CNT han atraído un interés considerable como dispositivos mecánicos a nanoescala debido a su extraordinaria sensibilidad con factores de alta calidad a una pequeña perturbación del entorno. Los resonadores de nanocables suspendidos basados en CNT son candidatos prometedores para aparatos que miden una amplia gama de cantidades físicas, como ondas EM [2], fuerzas pequeñas [7], masas [8], temperaturas [9] y ruidos [10].

Se requieren análisis de la evolución de la fase cuántica en las oscilaciones de nanocables para dilucidar teóricamente las características subyacentes del sistema. Con respecto a los estados de vibración cuántica de los resonadores de nanocables basados en CNT [11], la fase geométrica [12], así como la fase dinámica habitual, emerge como una evolución complementaria de la fase. La fase geométrica [12] es una anholonómica de estado cuántico que puede ser aplicable en diversos campos de la física. Los análisis de la fase geométrica se pueden adoptar potencialmente para caracterizar las propiedades nano de los nanocables, como los perfiles de resonancia [13, 14], las vibraciones cuánticas fuertes [15, 16], los mecanismos de relajación de deformaciones [17, 18], la aparición de magnetoplasmones de Dirac [19] y la topología de las oscilaciones de Aharonov-Bohm [20].

El estudio de la fase geométrica asociada con la dinámica no adiabática puede proporcionar una idea de los sistemas nanomecánicos, que es necesaria para el avance de técnicas de simulación precisas [21]. La preparación, manipulación y detección de estados cuánticos son factores importantes en las tecnologías cuánticas. El objetivo de la presente investigación es arrojar luz sobre los comportamientos temporales de la fase geométrica que tiene lugar en los estados cuánticos de las oscilaciones de nanocables. Para comprender el mecanismo de las vibraciones de nanocables basadas en CNT, investigaremos la evolución temporal de la fase geométrica en el estado comprimido, que es un estado cuántico de tipo clásico como el estado coherente. El mérito del estado comprimido es que la incertidumbre de una cuadratura en ese estado se puede reducir sustancialmente a expensas de aumentar la incertidumbre de la otra cuadratura, mientras que tal modulación de la incertidumbre es imposible en el estado coherente. En particular, analizaremos los efectos de la resonancia sobre la fase geométrica. Debido a que la energía resonante es significativamente diferente de la energía del estado no resonante [22, 23], el comportamiento topológico de la función de onda no es trivial y puede desviarse considerablemente del que se encuentra en situaciones normales. También se analizará rigurosamente la influencia del cambio de parámetros físicos y los parámetros de compresión en la evolución de la fase geométrica. Las fases geométricas son omnipresentes en los sistemas dinámicos [24] y se pueden aplicar a varias tecnologías modernas, como la computación cuántica [25], interferometrías de intensidad [26], multitarea fotónica [27], protocolos de detección cuántica [28] y ondas. -medidas de estabilidad [29].

El hamiltoniano del sistema implica funciones de tiempo asociadas con la amortiguación del sistema y la fuerza impulsora externa. Por lo tanto, el sistema es una especie de sistemas hamiltonianos dependientes del tiempo (TDHS) de los cuales los problemas de la mecánica cuántica se han estudiado ampliamente hasta hace poco. La función de tiempo en el hamiltoniano de un TDHS no se puede separar de la función de variables canónicas en la mayoría de los casos, lo que hace que el método convencional de separación de variables para resolver la ecuación de Schrödinger no esté disponible. Un método alternativo poderoso desarrollado para superar esta dificultad es el método del operador invariante que ha sido introducido por Lewis y Riesenfeld [30, 31]. Este método es una herramienta matemática muy útil cuando derivamos soluciones cuánticas de un TDHS. Muchos problemas de la mecánica cuántica descritos por los TDHS se investigan con base en este método. Por ejemplo, incluyen la dispersión caótica de partículas [32], la propagación de la luz en medios que varían en el tiempo [33], el control de electrones impulsados atrapados [34] y la no clasicidad de los circuitos nanoelectrónicos cuánticos [35]. Existe una variedad de otros métodos para los tratamientos mecánicos cuánticos de los TDHS, que incluyen el método de transformación unitaria [36], el método algebraico de Lie [37] y el método de estimación hamiltoniano [38].

En cuanto a que el sistema es un TDHS, utilizamos el método del operador invariante para obtener soluciones cuánticas del sistema. Se introducirá un operador invariante lineal que se representa en términos del operador de aniquilación. Si bien los operadores de aniquilación y creación se representan en términos de tiempo debido a la dependencia del tiempo del sistema, tanto el estado coherente como el comprimido se pueden obtener utilizando estos operadores de escalera. La fase geométrica del sistema se evaluará analíticamente utilizando la función de onda en el estado comprimido. La evolución temporal de la fase geométrica se analizará en detalle sobre la base de sus ilustraciones representadas con diversas opciones de parámetros.

Métodos

Para investigar la fase geométrica, primero necesitamos configurar la ecuación clásica de movimiento de la punta del nanoalambre. Debido a que la fase geométrica aparece en la evolución de onda cuántica de un TDHS, es necesario derivar funciones de onda en un estado cuántico específico que manejamos. Consideraremos el estado comprimido como se menciona en la parte introductoria. Las funciones de onda en los diversos estados cuánticos de un TDHS, incluido el estado comprimido, se pueden obtener mediante el método del operador invariante.

La ecuación de movimiento para la amplitud dependiente del tiempo x para un modo de flexión de un nanotubo de carbono suspendido con una masa efectiva m viene dado por [1]

$$ \ ddot {x} + \ left (\ frac {\ omega_ {0}} {Q} + \ eta x ^ {2} \ right) \ dot {x} + \ left (\ omega_ {0} ^ { 2} + \ beta x ^ {2} \ right) x =f _ {\ mathrm {d}} \ cos (\ omega t), $$ (1)

donde ω ₀ es la frecuencia angular resonante, Q el factor de calidad, f _d la fuerza impulsora electrostática dividida por m , η el coeficiente de amortiguamiento no lineal, y β el parámetro Duffing. Supongamos por conveniencia que el desplazamiento de la punta es suficientemente pequeño en relación con la longitud del cable CNT. Entonces, podemos despreciar los términos no lineales en la ecuación. (1), que conduce a [2]

$$ \ ddot {x} + \ frac {\ omega_ {0}} {Q} \ dot {x} + \ omega_ {0} ^ {2} x =f _ {\ mathrm {d}} \ cos (\ omega t). $$ (2)

El hamiltoniano del sistema que produce la ecuación. (2) viene dado por

$$ \ hat {H} =e ^ {- \ gamma t} \ frac {\ hat {p} ^ {2}} {2m} + \ frac {1} {2} me ^ {\ gamma t} \ left [\ omega_ {0} ^ {2} \ hat {x} ^ {2} - 2f _ {\ mathrm {d}} \ cos (\ omega t) \ hat {x} \ right], $$ (3)

donde γ = ω ₀ / Q . La solución clásica de la ecuación. (2) está compuesto por una función complementaria X _c ( t ) y una solución particular X _p ( t ), que están dados por

$$ \ begin {array} {@ {} rcl @ {}} &&X_ {c} (t) =X_ {c, 0} e ^ {- \ gamma t / 2} \ cos (\ Omega t + \ varphi) , \ end {matriz} $$ (4) $$ \ begin {matriz} {@ {} rcl @ {}} &&X_ {p} (t) =X_ {p, 0} \ cos (\ omega t - \ delta), \ end {matriz} $$ (5)

donde X _{c , 0} es una constante, \ (\ Omega =\ sqrt {\ omega _ {0} ^ {2} - \ gamma ^ {2} / 4} \), φ es una fase arbitraria, y

$$ \ begin {array} {@ {} rcl @ {}} X_ {p, 0} &=&\ frac {f _ {\ mathrm {d}}} {\ sqrt {\ left (\ omega_ {0} ^ {2} - \ omega ^ {2} \ right) ^ {2} + \ gamma ^ {2} \ omega ^ {2}}}, \ end {matriz} $$ (6) $$ \ begin {matriz} {@ {} rcl @ {}} \ delta &=&\ tan ^ {- 1} \ frac {\ gamma \ omega} {\ omega_ {0} ^ {2} - \ omega ^ {2}}. \ end {matriz} $$ (7)

La solución clásica en el espacio del momento se da de manera similar, donde la función complementaria es \ (P_ {c} (t) =me ^ {\ gamma t} \ dot {X} _ {c} (t) \) y la solución particular es \ (P_ {p} (t) =me ^ {\ gamma t} \ dot {X} _ {p} (t) \). Para investigar la fase geométrica del sistema, primero necesitamos derivar soluciones cuánticas. Observe que el hamiltoniano del sistema dado en la ecuación. (3) depende explícitamente del tiempo. Para derivar soluciones cuánticas del sistema, usamos el método del operador invariante [30, 31], que es un método útil cuando tratamos un sistema que varía en el tiempo. Un operador invariante \ (\ hat {I} \) del sistema se puede derivar de la ecuación de Liouville-von Neumann, que viene dada por \ ({d \ hat {I}} / {dt} ={\ partial \ hat {I}} / {\ t parcial} + \ left [\ hat {I}, \ hat {H} \ right] / \ left (i \ hbar \ right) =0 \). Por lo tanto, a partir de una evaluación rigurosa después de insertar la ecuación. (3) en esta ecuación, tenemos un operador invariante lineal [34] de la forma

$$ \ hat {I} =\ hat {A} e ^ {i \ Omega t}, $$ (8)

donde \ (\ hat {A} \) es el operador de aniquilación dado por

$$ \ begin {alineado} \ hat {A} =&\ left (2 \ hbar m \ Omega \ right) ^ {- 1/2} \ left [m \ left (\ Omega + i \ frac {\ gamma} { 2} \ right) e ^ {\ gamma t / 2} \ left [\ hat {x} -X_ {p} (t) \ right] \ right. \\ &\ left. + Ie ^ {- \ gamma t / 2} \ left [\ hat {p} -P_ {p} (t) \ right] \! {\ vphantom {\ left (\ Omega + i \ frac {\ gamma} {2} \ right)}} \ right]. \ end {alineado} $$ (9)

El adjunto hermitiano de Eq. (9), \ (\ hat {A} ^ {\ dagger} \), es el operador de creación.

Podemos expresar la ecuación de valor propio de \ (\ hat {A} \) como

$$ \ hat {A} | A \ rangle =A | A \ rangle. $$ (10)

Al evaluar la ecuación anterior, tenemos la expresión del valor propio tal que

$$ A (t) =A (0) e ^ {- i \ Omega t}, $$ (11)

donde A (0) = A ₀ e ^{- i φ} con

$$ A_ {0} =\ left [m \ Omega / (2 \ hbar) \ right] ^ {1/2} X_ {c, 0}. $$ (12)

Mientras que el estado coherente | A 〉 Es el autoestado de \ (\ hat {A} \), el estado comprimido es el autoestado de un operador \ (\ hat {B} \) que viene dado por

$$ \ hat {B} =\ mu \ hat {A} + \ nu \ hat {A} ^ {\ dagger}, $$ (13)

donde μ y ν son variables complejas que producen la ecuación

$$ | \ mu | ^ {2} - | \ nu | ^ {2} =1. $$ (14)

Si escribimos la ecuación de valor propio de \ (\ hat {B} \) en la forma

$$ \ hat {B} | B \ rangle =B | B \ rangle, $$ (15)

| B 〉 Es el estado exprimido. Al resolver esta ecuación en el espacio de configuración, tenemos

$$ {\ begin {alineado} \ langle {x} | B \ rangle =&^ {4} \! \! \! \ sqrt {\ frac {m \ Omega e ^ {\ gamma t}} {\ hbar \ pi (\ mu- \ nu) (\ mu ^ {*} - \ nu ^ {*})}} \ exp \ left \ {- \ frac {1} {\ hbar (\ mu- \ nu)} \ left [\ frac {1} {2} me ^ {\ gamma t} \ left ({\ vphantom {\ frac {1} {2}}} (\ mu + \ nu) \ Omega \ right. \ right. \ right. \\ &\ left. + \ frac {i \ gamma} {2} (\ mu- \ nu) \ right) \ left [x-X_ {p} (t) \ right] ^ {2} - [iP_ { p} (t) (\ mu- \ nu) + \ left (2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2} \\ &\ left. \ left. \ times (\ mu A + \ nu A ^ {*})] \ left [x-X_ {p} (t) \ right] {\ vphantom {\ frac {1} {2} yo ^ {\ gamma t}}} \ right] - \ frac {| A | ^ {2} + A ^ {2}} {2 (\ mu- \ nu) (\ mu ^ {*} - \ nu ^ {*})} \derecho\}. \ end {alineado}} $$ (16)

Por tanto, la función de onda en el estado comprimido se ha obtenido como se indica en la ecuación. (dieciséis). Las características cuánticas del sistema pueden aclararse sobre la base de dicha descripción analítica de la función de onda. Para μ =1 y ν =0, ecuación. (16) se reduce a la función de onda en el estado coherente, que es el autoestado de la Ec. (10) en el espacio de configuración. La función de onda, Eq. (16), se utilizará en la siguiente sección para derivar la fase geométrica en el estado comprimido.

Resultados y discusión

Es bien sabido que la fase en la evolución de la onda cuántica involucra tanto la fase geométrica como la fase dinámica. La fase geométrica fue descubierta por primera vez por Berry en 1984 [12] para un sistema que evoluciona cíclicamente con un cambio adiabático. Según el teorema adiabático en mecánica cuántica, un autoestado instantáneo de un estado cuántico en una evolución cíclica en el espacio de parámetros permanecerá en el mismo estado más tarde, mientras que hay una acumulación adicional de la fase cuántica que es la fase Berry. Una generalización de la fase Berry de manera que incluya la evolución no adiabática, no cíclica y / o no unitaria del sistema cuántico es la fase geométrica.

La fase geométrica en el estado comprimido viene dada por

$$ \ gamma_ {G} (t) =\ int_ {0} ^ {t} \ langle B (t ') | i \ frac {\ parcial} {\ parcial t'} | B (t ') \ rangle dt' + \ gamma_ {G} (0). $$ (17)

La diferenciación de la función de onda con respecto al tiempo en el espacio de configuración se convierte en

$$ \ frac {\ parcial \ langle {x} | B \ rangle} {\ parcial t} \, =\, \ left \ {f_ {1} (t) \! \ left [x-X_ {p} ( t) \ derecha] ^ {2} \, + \, f_ {2} (t) \ izquierda [x \, - \, X_ {p} (t) \ derecha] \, + \, f_ {3} ( t) \ derecha \} \! \! \ langle {x} | B \ rangle, $$ (18)

donde

$$ f_ {1} (t) =- \ frac {m \ gamma e ^ {\ gamma t}} {2 \ hbar (\ mu- \ nu)} \ left ((\ mu + \ nu) \ Omega + \ frac {i \ gamma} {2} (\ mu- \ nu) \ right), $$ (19) $$ {\ begin {alineado} f_ {2} (t) &=\ frac {1} {\ hbar (\ mu- \ nu)} \ left [\ left ((\ mu + \ nu) \ Omega + \ frac {i \ gamma} {2} (\ mu- \ nu) \ right) P_ {p} (t) -ime ^ {\ gamma t} \ right. \\ &\ quad \ times \ left [\ omega_ {0} ^ {2} X_ {p} (t) - f _ {\ mathrm {d}} \ cos (\ omega t) \ right] (\ mu- \ nu) + \ left (2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2} \\ &\ quad \ left. \ times \ izquierda (\ frac {\ gamma} {2} \ izquierda (\ mu A + \ nu A ^ {*} \ derecha) -i \ Omega \ izquierda (\ mu A - \ nu A ^ {*} \ derecha) \ derecha) \ derecha], \\ \ end {alineado}} $$ (20) $$ {\ begin {alineado} f_ {3} (t) &\! =\ frac {\ gamma} {4} - \ frac {1} {\ hbar me ^ {\ gamma t} (\ mu- \ nu)} \ left [iP_ {p} (t) (\ mu- \ nu) + \ left (2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2} \ right. \\ &\ quad \ left. \ times \ left (\ mu A + \ nu A ^ {*} \ right) {\ vphantom {\ left ( 2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2}}} \ right] P_ {p} (t) + \ frac {i \ Omega A ^ {2}} {(\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)}. \ end {alineado}} $$ (21)

Evaluación adicional después de insertar la ecuación. (18) en la ecuación. (17) da

$$ {\ begin {alineado} \ gamma_ {G} (t) =&\ int_ {0} ^ {t} dt '\ left [A_ {0} ^ {2} \ left (\ frac {\ gamma ^ { 2}} {4 \ Omega} + \ Omega + g_ {1} \ sin \ left [2 \ left (\ Omega t '+ \ varphi \ right) \ right] + g_ {2} \ cos \ left [2 \ izquierda (\ Omega t '+ \ varphi \ right) \ right] \ right) \ right. \\ &\ left.-A_ {0} \ left [g_ {3} (t') \ sin \ left (\ Omega t '+ \ varphi \ right) + g_ {4} (t') \ cos \ left (\ Omega t '+ \ varphi \ right) \ right] + g_ {5} (t') {\ vphantom {\ frac {\ gamma ^ {2}} {4 \ Omega}}} \ right] + \ gamma_ {G} (0), \ end {alineado}} $$ (22)

donde

$$ \ begin {array} {* {20} l} g_ {1} ~ &=\ frac {\ gamma} {2} + \ frac {i \ Omega \ left (\ mu \ nu ^ {*} - \ mu ^ {*} \ nu \ right)} {(\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)}, \ end {matriz} $$ (23) $$ \ begin {array} {* {20} l} g_ {2} ~ &=\ frac {\ gamma ^ {2}} {4 \ Omega} + \ Omega \ frac {2 | \ nu | ^ {2 } - \ left (\ mu \ nu ^ {*} + \ mu ^ {*} \ nu \ right)} {(\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)}, \ end {matriz} $$ (24) $$ \ begin {matriz} {* {20} l} g_ {3} (t) &=\ left (\ frac {2 \ Omega} {m \ hbar e ^ {\ gamma t}} \ right) ^ {1/2} P_ {p} (t), \ end {matriz} $$ (25) $$ {\ begin {alineado} g_ {4} ( t) =\ frac {1} {\ sqrt {2 \ hbar \ Omega}} \ left (\ frac {\ gamma} {\ sqrt {me ^ {\ gamma t}}} P_ {p} (t) - 2 \ sqrt {me ^ {\ gamma t}} \ left [\ omega_ {0} ^ {2} X_ {p} (t) - f _ {\ mathrm {d}} \ cos (\ omega t) \ right] \ derecha), \ end {alineado}} $$ (26) $$ {\ begin {alineado} g_ {5} (t) &=\ frac {P_ {p} ^ {2} (t)} {\ hbar yo ^ {\ gamma t}} + \ frac {\ gamma ^ {2}} {8 \ Omega} \ left [2 | \ nu | ^ {2} - \ left (\ mu \ nu + \ mu ^ {*} \ nu ^ {*} \ right) +1 \ right] \\ &\ quad + \ frac {i \ gamma} {4 (\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {* } \ right)} \ left [| \ mu | ^ {2} \ left (\ nu ^ {2} - \ nu ^ {* 2} \ right) - | \ nu | ^ {2} \ lef t (\ mu ^ {2} - \ mu ^ {* 2} \ right) \ right. \\ &\ quad \ left. + (2 | \ nu | ^ {2} +1) \ left (\ mu \ nu ^ {*} - \ mu ^ {*} \ nu \ right) + (\ mu- \ mu ^ {*}) (\ nu- \ nu ^ {*}) \ right]. \ end {alineado}} $$ (27)

El último término en g ₅ que contiene ( μ - μ ^∗ ) ( ν - ν ^∗ ) es inadecuado como fase porque se trata de un número puramente imaginario. Por lo tanto, ahora eliminamos este término eligiendo al menos uno de μ y ν como valor real. Este remedio siempre se puede hacer sin pérdida de generalidad, porque solo la fase relativa entre μ y ν tiene un significado físico en lugar de sus fases absolutas.

A partir de la ejecución de la integración en Eq. (22), tenemos

$$ {\ begin {alineado} \ gamma_ {G} (t) &=A_ {0} ^ {2} \ left [\ left (\ frac {\ gamma ^ {2}} {4 \ Omega} + \ Omega \ right) t + \ frac {g_ {1}} {\ Omega} \ sin (\ Omega t + 2 \ varphi) \ sin (\ Omega t) + \ frac {g_ {2}} {\ Omega} \ cos (\ Omega t + 2 \ varphi) \ right. \\ &\ quad \ left. \ Times \ sin (\ Omega t) {\ vphantom {\ frac {\ gamma ^ {2}} {4 \ Omega}}} \ right] \! - A_ {0} \ left [\ left (\ frac {2m \ Omega} {\ hbar} \ right) ^ {1/2} \ omega X_ {p, 0} \ bar {g} _ {3} (t) + \ sqrt {\ frac {2m} {\ hbar \ Omega}} \ frac {1} {4 \ omega ^ {2} + \ gamma ^ {2}} \ bar {g} _ { 4} (t) \ right] \\ &\ quad + \ bar {g} _ {5} (t) + \ gamma_ {G} (0), \ end {alineado}} $$ (28)

donde \ (\ bar {g} _ {i} (t) ~ (i =3,4,5) \) están dados por

$$ \ bar {g} _ {i} (t) =G_ {i} (t) -G_ {i} (0), $$ (29)

con

$$ {\ begin {alineado} G_ {3} (\ tau) &=e ^ {\ gamma \ tau / 2} \ left (\ frac {1} {4 (\ Omega + \ omega) ^ {2} + \ gamma ^ {2}} \ left \ {2 (\ Omega + \ omega) \ sin [(\ Omega + \ omega) \ tau + \ varphi- \ delta] \ right. \ right. \\ &\ quad \ left. + \ gamma \ cos [(\ Omega + \ omega) \ tau + \ varphi- \ delta] \ right \} - \ frac {1} {4 (\ Omega- \ omega) ^ {2} + \ gamma ^ {2}} \ {2 (\ Omega- \ omega) \\ &\ quad \ left. \ Left. \ Times \ sin [(\ Omega- \ omega) \ tau \, + \, \ varphi \, + \, \ delta] \ ! + \ gamma \ cos [(\ Omega- \ omega) \ tau \, + \, \ varphi \, + \, \ delta] \ right \} {\ vphantom {\ frac {1} {4 (\ Omega + \ omega) ^ {2} + \ gamma ^ {2}}}} \ right), \\ \ end {alineado}} $$ (30) $$ {\ begin {alineado} G_ {4} (\ tau) &=e ^ {\ gamma \ tau / 2} \ left \ {X_ {p, 0} \ left \ {\ gamma \ omega [2 \ omega \ cos (\ omega \ tau- \ delta) - \ gamma \ sin ( \ omega \ tau- \ delta)] -2 \ omega_ {0} ^ {2} \ right. \ right. \\ &\ quad \ left. \ times [2 \ omega \ sin (\ omega \ tau- \ delta ) + \ gamma \ cos (\ omega \ tau- \ delta)] {\ vphantom {X_ {p, 0}}} \ right \} + 2f _ {\ mathrm {d}} [2 \ omega \ sin (\ omega \ tau) \\ &\ left. \ left. \ quad + \ gamma \ cos (\ omega \ tau) \ right] {\ vphantom {X_ {p, 0}}} \ right \}, \\ \ end {alineado }} $$ ( 31) $$ {\ begin {alineado} G_ {5} (\ tau) &=\ frac {m \ omega ^ {2}} {2 \ hbar} X_ {p, 0} ^ {2} \ frac {e ^ {\ gamma \ tau}} {\ gamma \ left (4 \ omega ^ {2} + \ gamma ^ {2} \ right)} \ left \ {\ gamma ^ {2} +4 \ omega ^ {2} - \ gamma ^ {2} \ cos [2 (\ omega \ tau - \ delta)] \ right. \\ &\ quad \ left.-2 \ gamma \ omega \ sin [2 (\ omega \ tau - \ delta )] {\ vphantom {\ gamma ^ {2} +4 \ omega ^ {2} - \ gamma ^ {2}}} \ right \} + \ frac {\ gamma ^ {2} \ tau} {8 \ Omega } \ left [2 | \ nu | ^ {2} - \ left (\ mu \ nu + \ mu ^ {*} \ nu ^ {*} \ right) +1 \ right] \\ &\ quad + \ frac {i \ gamma \ tau} {4 (\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)} \ left [| \ mu | ^ {2} \ left (\ nu ^ {2} - \ nu ^ {* 2} \ right) - | \ nu | ^ {2} \ left (\ mu ^ {2} - \ mu ^ {* 2} \ right) \ right. \\ &\ quad \ left. + \ left (2 | \ nu | ^ {2} +1 \ right) \ left (\ mu \ nu ^ {*} - \ mu ^ {*} \ nu \ right) \ right]. \ end {alineado}} $$ (32)

Por lo tanto, hemos evaluado la fase geométrica completa en el estado comprimido, que viene dada por la Ec. (28) con las Ecs. (23), (24) y (29) - (32).

La evolución en el tiempo de la fase geométrica se ha ilustrado en las Figs. 1, 2, 3 y 4. De la Fig. 1, vemos que la fase geométrica oscila y la envolvente de dicha oscilación aumenta con el tiempo. El aumento de la envolvente es mayor cuando A ₀ es largo. El patrón de oscilación se vuelve gradualmente irregular a medida que los valores de μ y ν aumento. Además, la amplitud de la oscilación aumenta a medida que pasa el tiempo.

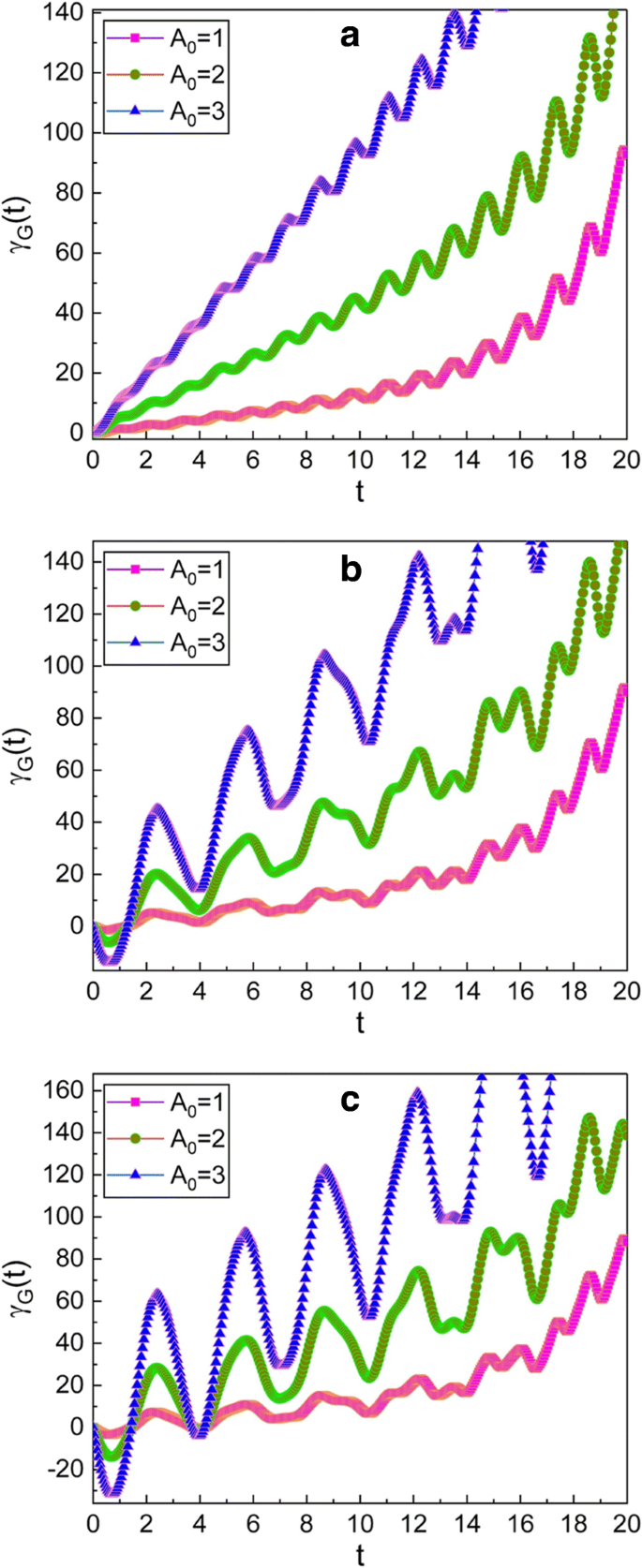
Evolución temporal de la fase geométrica para varios valores diferentes de A ₀ . Los valores de ( μ , ν ) utilizados en los gráficos son (1, 0) para a , (\ (\ sqrt {2} \), 1) para b y (\ (\ sqrt {3} \), \ (\ sqrt {2} \)) para c . Hemos utilizado m =1, ω ₀ =1, ω =5, γ =0.35, f _d =1, \ (\ hbar =1 \), φ =0 y γ _G (0) =0. La fase y todos los parámetros se consideran adimensionales por conveniencia, y esta convención también se aplicará a las figuras siguientes. Porque A ₀ se da en términos de la amplitud clásica X _{c , 0} de la función complementaria [ver Eq. (12)], podemos confirmar a partir de los gráficos que la fase geométrica es grande cuando la amplitud de oscilación es alta. También vemos que la fluctuación de γ _G ( t ) se vuelve grande a medida que los valores μ y ν aumentar bajo la condición dada en Eq. (14)

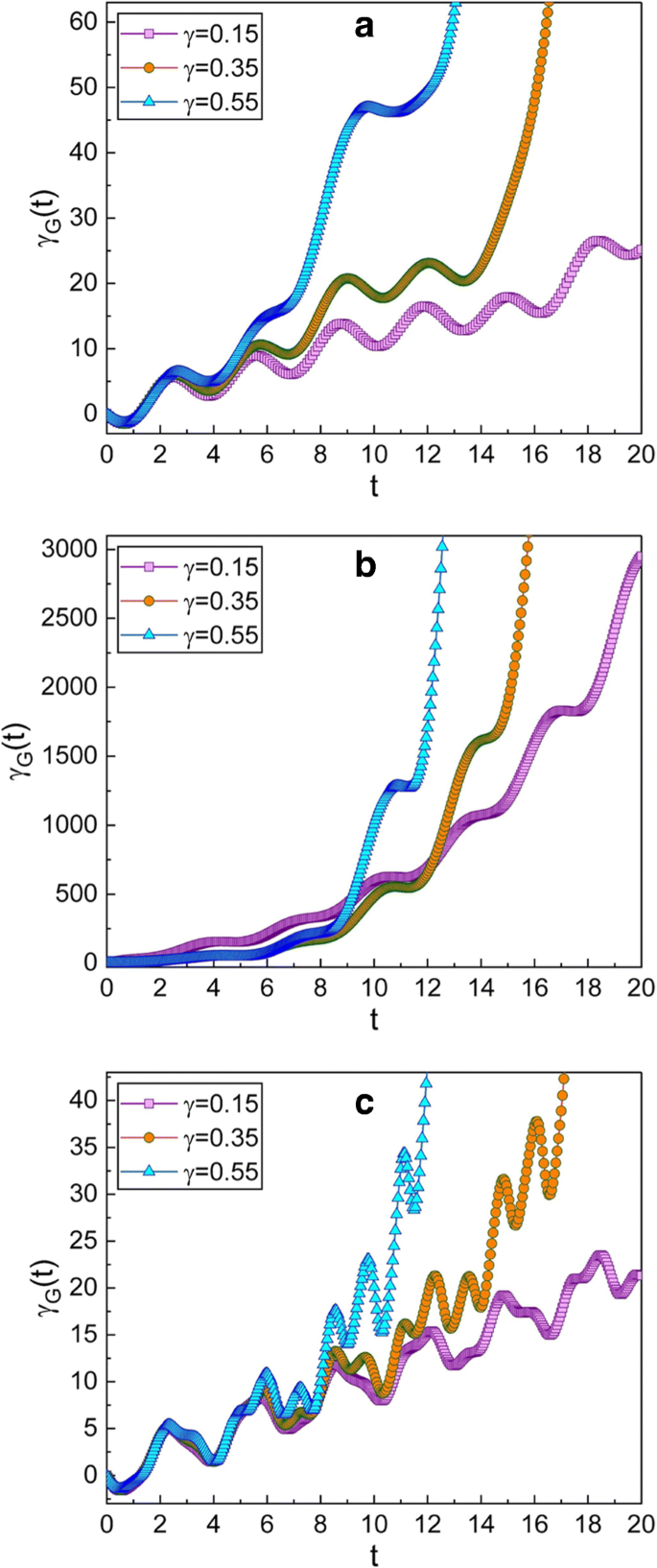
Evolución temporal de la fase geométrica para varios valores diferentes de γ . El valor de ω usado en los gráficos es 0.3 para a , 0,99 para b y 5 para c . Los parámetros de compresión elegidos aquí son \ (\ mu =\ sqrt {2} \) y ν =1; esta elección da q - estado exprimido en el momento inicial. Otras cantidades que hemos utilizado son m =1, ω ₀ =1, A ₀ =1, f _d =1, \ (\ hbar =1 \), φ =0 y γ _G (0) =0. Confirmamos que la fase geométrica es grande cuando el factor de amortiguamiento γ es grande en la mayoría de los casos, pero no en todos. La frecuencia del caso b está cerca de la frecuencia de resonancia, mientras que los de a y c están lejos del resonante. La fase geométrica del caso resonante ( b ) aumenta muy rápidamente con el tiempo

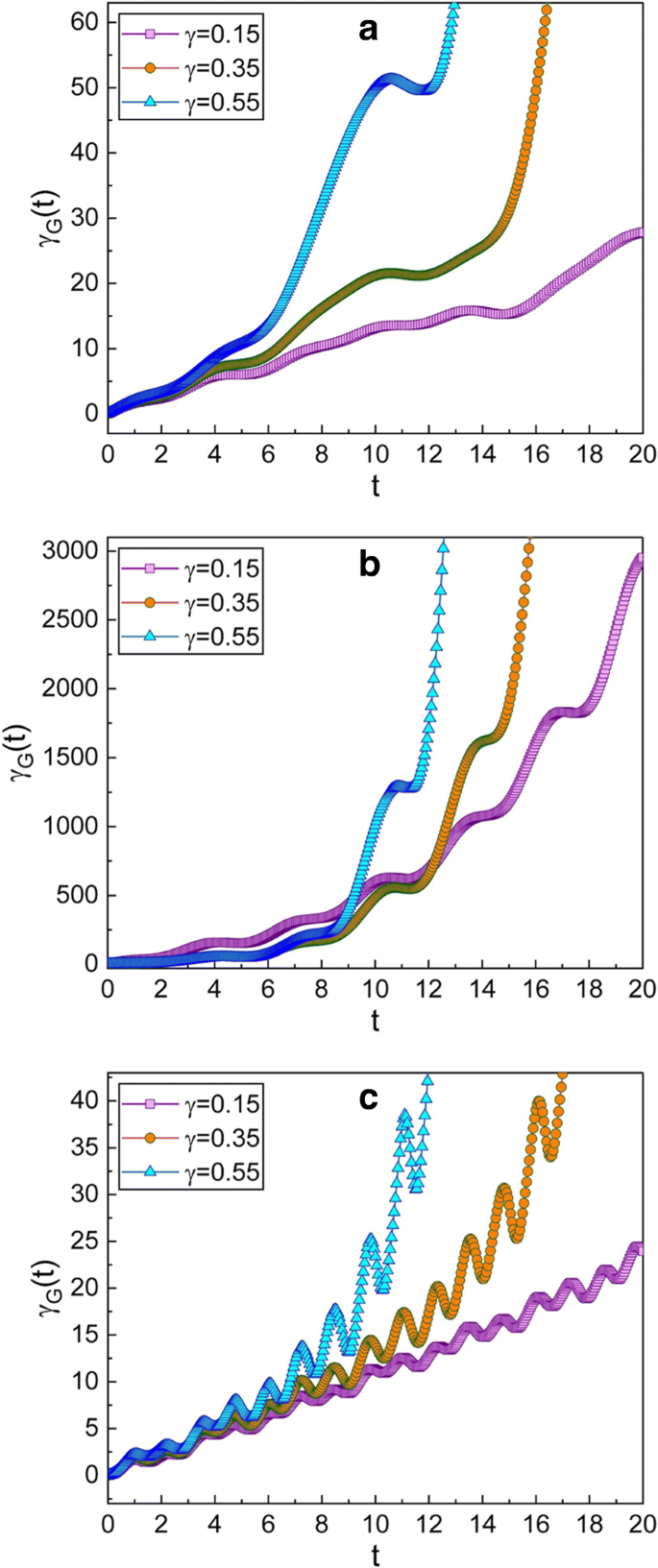
un - c Este gráfico es el mismo que el de la Fig.2, pero para el caso de que los parámetros de compresión elegidos sean \ (\ mu =\ sqrt {2} \) y ν =−1 que dan una p - estado exprimido en el momento inicial. Del hecho de que los gráficos generales en este caso no son tan diferentes de los correspondientes de la Fig.2, podemos confirmar que la evolución de γ _G ( t ) es casi irrelevante para los tipos de compresión siempre que los valores absolutos de μ y ν no cambie

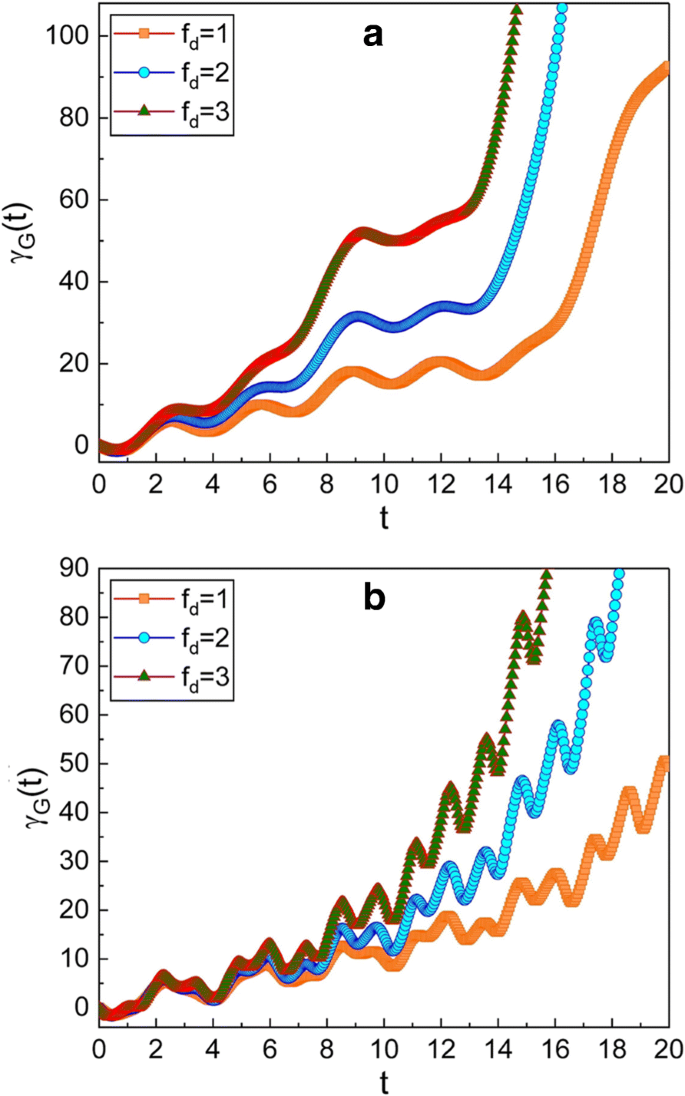
Evolución temporal de la fase geométrica para varios valores diferentes de f _d . El valor de ω usado en los gráficos es 0.3 para a y 5 para b . Hemos utilizado \ (\ mu =\ sqrt {2} \), ν =1, m =1, ω ₀ =1, γ =0.3, A ₀ =1, \ (\ hbar =1 \), φ =0 y γ _G (0) =0. Como la amplitud ( f _d ) de la fuerza impulsora aumenta, la fase geométrica se vuelve grande

Los efectos de compresión en el estado comprimido según el parámetro de compresión c donde c = μ / ν ha sido investigado en la ref. [39]. Según el análisis dado en la ref. [39] (ver Fig. 1 (a) en la ref. [39]), el estado comprimido ilustrado en la Fig. 2, que corresponde a \ (c =\ sqrt {2} \), es el q -exprimido en el momento inicial, mientras que el de la Fig. 3, que corresponde a \ (c =- \ sqrt {2} \), es el p -Estado exprimido en la misma situación. Comparando las Figs. 2 y 3 entre sí, podemos concluir que la fase geométrica en el q -exprimido es casi el mismo que en el p -estado comprimido.

Los efectos de γ sobre la evolución de la fase geométrica se puede confirmar a partir de las Figs. 2 y 3. La fase geométrica aumenta más rápidamente cuando γ es largo. Comparando las Figs. 2a y 3a con las Figs. 2c y 3c, podemos confirmar que la fase geométrica varía algo rápidamente cuando ω es mayor que la frecuencia angular de resonancia.

El comportamiento temporal de la fase geométrica en o cerca del estado resonante del sistema puede ser de gran interés [22, 23]. Las figuras 2b y 3b muestran que la fase geométrica aumenta muy rápidamente cuando ω está cerca de la frecuencia angular de resonancia. Esto significa que la función de onda en esta situación varía significativamente con el tiempo, porque la magnitud de la fase geométrica está relacionada con la variación en el tiempo de la función de onda. De hecho, la amplitud de la oscilación del cable aumenta notablemente en el estado de resonancia. Por cierto, las frecuencias angulares de resonancia de los resonadores de nanocables suspendidos basados en CNT no solo son altas, sino que también son ampliamente sintonizables con factores de muy alta calidad [3]. Por esta razón, los modos vibratorios del sistema se mantendrán durante mucho tiempo hasta que se amortigüen por completo [11].

La figura 4 muestra que la fase geométrica también se ve afectada por la amplitud de la fuerza impulsora f _d . Como f _d aumenta, el incremento de la fase geométrica en el tiempo es rápido.

Conclusión

Hemos investigado la fase geométrica en el estado comprimido para el sistema sobre la base de la dinámica cuántica con la ecuación de Schrödinger. Con respecto a la dependencia del tiempo del hamiltoniano que describe el sistema, se ha introducido el método del operador invariante, que es una herramienta potencial para derivar soluciones cuánticas en el caso en que el hamiltoniano se describe en términos de tiempo. Mediante este método se ha obtenido la fórmula analítica de la fase geométrica para la oscilación de nanocables basada en CNT.

Se ha realizado un análisis detallado de los efectos de fase, necesario para una comprensión teórica de las vibraciones mecánicas. Nuestro desarrollo de la fase geométrica es completamente cuántico con rigurosas evaluaciones matemáticas. La fase geométrica es sensible al cambio de parámetros mecánicos y presenta una oscilación en un gran número de casos. También se ha analizado la influencia de los parámetros de compresión en la evolución de la fase geométrica. Hemos confirmado un fuerte aumento de la acumulación de fase geométrica a lo largo del tiempo cerca de la frecuencia angular resonante.

Nuestros resultados ilustran el comportamiento temporal de la fase geométrica que aparece en la vibración de un nanoalambre basado en CNT. El análisis de la fase geométrica dado en este trabajo es importante para comprender no solo las características topológicas del sistema, sino también las vibraciones dinámicas de otros osciladores mecánicos basados en nanocables. En particular, hemos desarrollado propiedades de fase del estado resonante, cuya aclaración es necesaria en la aplicación del sistema en tecnologías de información cuántica y otras industrias de base cuántica [40]. El método y marco similar utilizado en esta investigación también se puede extender a otros nano sistemas, tales como resonadores superconductores Fabry-Perot [41], nano voladizos [42] y sistemas híbridos qubit-resonador-átomo [43].