Predicción del efecto Hall cuántico anómalo en MBi y MSb (M:Ti, Zr y Hf) Panales

Antecedentes

Los rigurosos esfuerzos de investigación se han centrado continuamente en la exploración de materiales 2D novedosos, como los aisladores Quantum Spin Hall (QSH). Estos nuevos materiales, también conocidos como aislantes topológicos bidimensionales (TI 2D) exhiben una propiedad única en la que los bordes poseen estados sin espacios con polarización de espín a pesar de que el sistema a granel es un aislante [1]. Los aisladores QSH muestran un transporte de carga / giro sin disipación, lo cual es muy importante en las aplicaciones de dispositivos espintrónicos [2]. Recientemente, se ha descubierto que la ruptura de la simetría de inversión de tiempo (TRS) en los aisladores QSH conduce a un sistema de efecto Hall anómalo cuántico (QAHE) en el que los estados de los bordes helicoidales se convierten en estados de los bordes quirales [3]. El transporte de carga sin disipación sin la necesidad de un campo magnético externo proporciona aplicaciones prometedoras en la espintrónica de bajo consumo de energía [4, 5] y ha alentado la búsqueda de más sistemas QAHE [6, 7]. Predeterminado por Haldane en 1988, QAHE solo se logró experimentalmente en 2013 mediante dopaje magnético de películas delgadas de aislantes topológicos [8]. Los estudios teóricos han sugerido que la fase de Hall anómala cuántica (QAH) se puede lograr rompiendo el TRS de un TI introduciendo ferromagnetismo e induciendo una transición de inversión de banda mediante fuertes efectos de acoplamiento espín-órbita (SOC) [9, 10]. Por lo tanto, los aisladores QSH son buenos materiales de partida para lograr QAHE. Varios estudios han predicho que las películas delgadas de los grupos IV (Sn) [11-13] y V (Bi, Sb) [6, 14-17] apoyan las fases QSH que también pueden lograrse mediante funcionalización química [17, 18]. Además de los elementos de los grupos IV y V, también se predijo que los panales [19-21] III-V apoyan la fase QSH tanto en los casos independientes como en los funcionalizados. Estos resultados allanaron el camino para encontrar fases de QAHE. Los estudios han demostrado que QAHE existía en películas delgadas de los grupos IV [22] y V [17, 18, 22] funcionalizados. Además, los cálculos de los primeros principios muestran QAHE en panales fluorados [23] y químicamente funcionalizados [24] III-V. Además, varios estudios teóricos han predicho que el dopaje con metales de transición en panales puede inducir fases de QAH [17, 25-27]. Esto se ha realizado experimentalmente mediante el dopaje con Cr y V [8, 28, 29]. Apoyado por el hallazgo de que los materiales en panal III-V son aislantes QSH [19] y la predicción teórica de que el dopaje de un material magnético puede inducir magnetismo [10], reemplazamos el elemento del grupo III con un metal de transición (M =Ti, Zr y Hf). Los carburos de metales de transición MC (M =Zr y Hf) [30] y los haluros de metales de transición MX (M =Zr y Hf) [31] son ​​también otra familia de materiales que se prevé que existan como aislantes QSH. Sin embargo, aún no se ha explorado su potencial para apoyar QAHE. Motivados por estos hallazgos, predecimos que las propiedades electrónicas de los pnictidos de metales de transición MPn (M =Ti, Zr y Hf; Pn =Sb y Bi) exhibirán la fase QAH. En este trabajo, empleamos cálculos de primeros principios para predecir la capacidad de los metales de transición (M =Ti, Zr y Hf) para inducir magnetismo intrínseco en panales Bi / Sb. Examinamos tanto casos pandeados como planos e identificamos los cambios de fase debidos a la deformación. Las fases de QAH se verifican calculando el número de Chern y observando la inversión de la banda.

Resultados y discusiones

Similar al panal Bi puro (con dos átomos en la celda unitaria) que puede adoptar estructuras planas y pandeadas, nuestro material se obtiene reemplazando la mitad de Bi por un metal de transición [por ejemplo, Ti, Zr y Hf] en la celda unitaria . La vista superior de M-Bi / Sb con una celda unitaria 1 × 1 delineada se muestra en la Fig. 1a, mientras que las vistas laterales de los panales M-Bi / Sb pandeados y planos se muestran en las Fig. 1b, c, respectivamente. La primera zona de Brillouin (BZ) correspondiente etiquetada con puntos de alta simetría se muestra en la Fig. 1d.

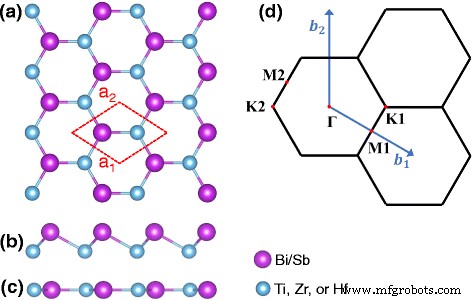
un Estructura cristalina de nido de abeja M-Sb / Bi. b , c Vistas laterales de estructuras pandeadas y planas, respectivamente. d La primera zona de Brillouin (BZ) con puntos de alta simetría

Estudiamos la estabilidad de los panales y el efecto de la tensión variando la constante de celosía y permitiendo que los átomos se relajen tanto para los casos pandeados como planos. A continuación, identificamos sus fases topológicas bajo diferentes cepas a través de los cálculos del número de Chern. El resultado se ilustra mediante un diagrama de fase como se presenta en la Fig. 2. Las curvas de energía para TiBi, ZrBi y HfBi se muestran en la Fig. 2a-c, respectivamente. Encontramos que los panales MBi poseen las fases planas y de pandeo bajo. A través de estas figuras, identificamos las constantes de la red de equilibrio para un análisis más detallado. La figura también muestra que MBi pandeado es la estructura energéticamente favorecida. Sin embargo, la mayoría de las fases de QAH se observan cuando se incrementa la deformación, lo que transforma el material de pandeo en panales planos. También debe tenerse en cuenta que las fases QAH se pueden observar en HfBi pandeado, pero solo dentro de un pequeño rango de constantes de celosía [ver Fig. 2c].

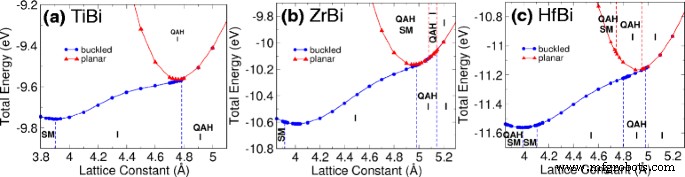
Diagrama de fases de a TiBi, b ZrBi y c HfBi que muestra la energía total en diferentes constantes de celosía. El diagrama se divide en varias regiones etiquetadas como QAH (fase de Hall anómala cuántica), I (aislante) y SM (semi-metálico). Los círculos azules y los triángulos rojos representan cajas abrochadas y planas, respectivamente

Las tablas 1 y 2 muestran las constantes reticulares de equilibrio para las estructuras M-Bi y M-Sb. También se indican la banda prohibida, el momento magnético, la fase y la clasificación del material asociados. QAHE está presente cuando el número de Chern calculado, C, es un número entero distinto de cero. La banda prohibida se calcula como la diferencia entre las bandas desocupadas más bajas y las ocupadas más altas. Nuestros cálculos muestran que la fase del aislante QAH se puede encontrar en TiBi y HfBi planar con brechas de banda de 15 y 7 meV, respectivamente. Además, la transición de fase se puede inducir en TiBi variando la distancia de pandeo [ver Fig. 3] e induciendo deformación en HfBi pandeado [Fig. 4]. En TiBi, encontramos que los cruces de bandas debido a la variación de la distancia de pandeo ocurren en los puntos de baja simetría mostrados en la Fig. 3d; mientras que en HfBi, observamos los dos cruces de banda (puntos críticos de transición) primero en K2 ( a =4.8 Å) y luego en K1 ( a =5.0 Å) debido a la deformación en la Fig. 4c, g.

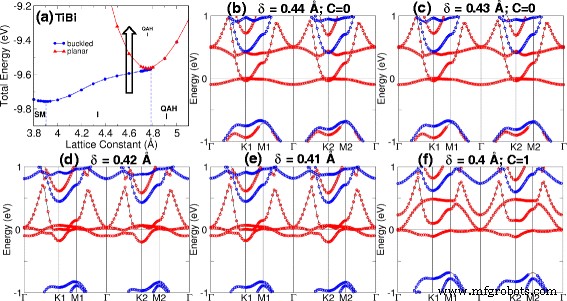
Transición de fase después de variar la distancia de pandeo. un Diagrama de fase de TiBi en a =4,6 Å. La flecha muestra el camino de la transición. b - f La transición de la estructura de la banda como la distancia de pandeo ( δ ) se redujo de 0,44 a 0,4 Å. La transición ocurre en δ =0,41 Å

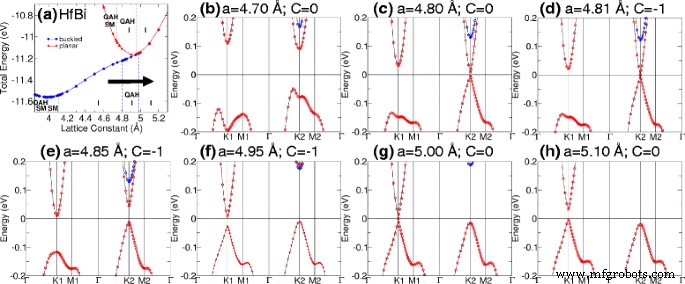
Transición de fase después de variar la constante de celosía. un Diagrama de fases de HfBi pandeado. La flecha muestra el camino de la transición. b - h La transición de la estructura de la banda como constante de celosía se incrementó de 4,7 a 5,1 Å

La Figura 5a, b muestra las estructuras de bandas electrónicas en las constantes de celosía de equilibrio para M-Bi y M-Sb en estructuras planas y pandeadas, respectivamente. Los círculos rojo y azul son las contribuciones de giro hacia arriba y hacia abajo, respectivamente. La fase QAH (con C =1) con la mayor banda prohibida es de 15 meV observado en TiBi plano. Planar HfBi también es un aislante QAH con una pequeña banda prohibida de 7 meV (con C =−1). Sin embargo, en una forma pandeada, HfBi es un semi-metal con un alto C =−3. Por otro lado, ZrBi, TiSb, ZrSb y ZrSb planos abrochados son aislantes triviales.

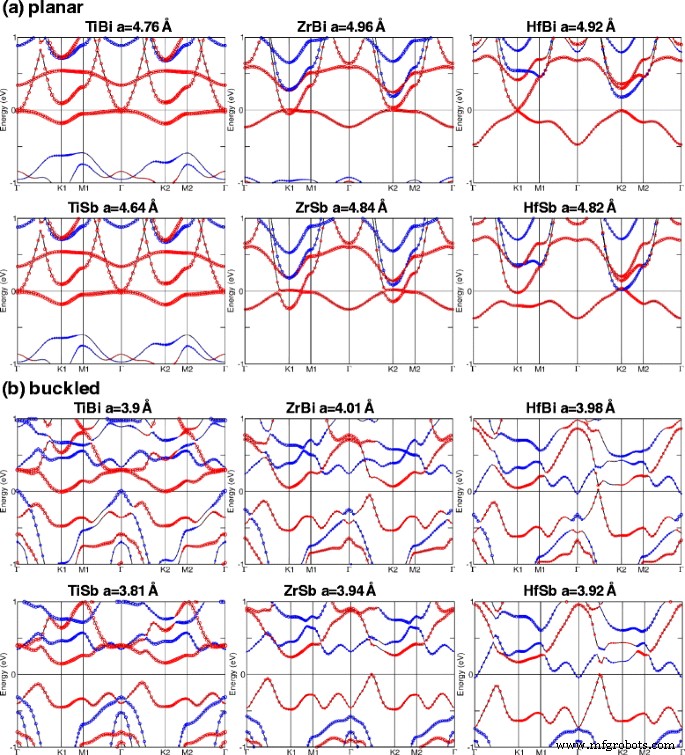
Estructuras de bandas electrónicas de M-Pn (M =Ti, Zr y Hf; Pn =Sb y Bi) en sus constantes de celosía de equilibrio para a planar y b casos abrochados. Las constantes de la red de equilibrio se dan por encima de la estructura de la banda. Los círculos rojos y azules indican + s _z y - s _z contribuciones, respectivamente

La naturaleza de QAHE se puede comprender mejor examinando los efectos del SOC en cálculos no magnéticos y ferromagnéticos. Para ello, elegimos TiBi planar (con a =4,76 Å) como ejemplo. Las estructuras de banda obtenidas en cálculos no magnéticos y ferromagnéticos con y sin SOC se muestran en la Fig. 6. Nuestros cálculos muestran que esta estructura tiene un momento magnético de 1.05 μ _B por unidad de celda que es principalmente aportada por átomos de Ti. En los cálculos no magnéticos, encontramos que el sistema es metálico [Fig. 6a, c]. Podemos observar en la Fig. 6b que se puede inducir un momento magnético neto debido al orden ferromagnético que está influenciado por el metal de transición, Ti. Además, el sistema ahora tiene estados de spin-up sin gap (líneas rojas) y estados de spin-down con gap, y aplicando SOC al cálculo ferromagnético, se obtiene un gap de 15 meV. Esto muestra que la inversión de la banda es inducida por SOC y la apertura de la brecha da como resultado QAHE.

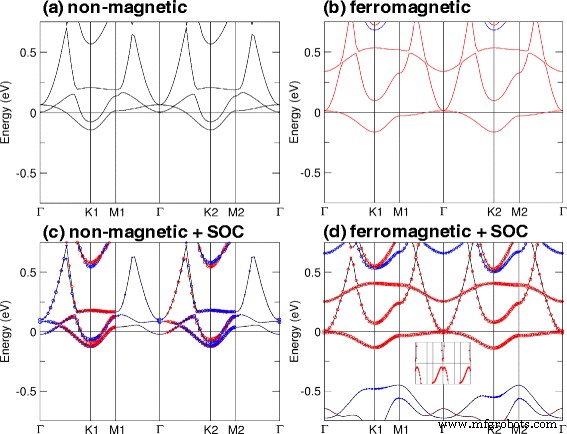
Estructuras de bandas electrónicas de película TiBi plana en a =4,76 Å para cálculos no magnéticos ( a ) sin SOC y ( c ) con SOC y cálculos ferromagnéticos ( b ) sin SOC y ( d ) con SOC. Los círculos rojos y azules indican + s _z y - s _z contribuciones, respectivamente, para ( c ) no magnético ( d cálculos ferromagnéticos) con SOC

Finalmente, inspeccionamos el espectro de la banda de borde del panal HfBi planar para detectar la presencia de estados de borde utilizando hamiltonianos de unión estrecha derivados a través de funciones de Wannier. Construimos cintas HfBi con bordes en zigzag y un ancho de 127 Å como se muestra en la Fig. 7. La figura también confirma la presencia de estados de borde indicados por y proporcionales al tamaño de los círculos rojo y azul que representan los bordes derecho e izquierdo, respectivamente. . Los estados de borde separados se deben a la asimetría de los bordes en zigzag derecho e izquierdo. También podemos observar un número impar de bandas de borde que cruzan el nivel de fermi. Encontramos que este número es el mismo que el valor absoluto del número de Chern, lo que confirma aún más la fase QAH en HfBi planar.

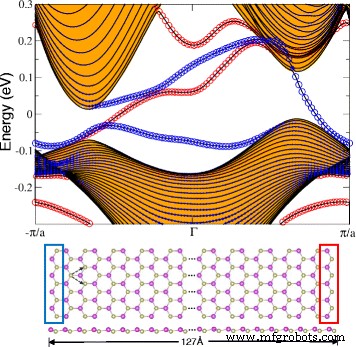
Estructura de banda a lo largo del borde de la nanocinta en zigzag de HfBi doblada con a =4,9 Å y el ancho de 127 Å. Los círculos azules (rojos) indican la contribución de los bordes izquierdo (derecho). Las bandas de volumen se indican mediante la región llena de naranja

Además, calculamos el espectro de fonones para cada sistema y notamos que estos sistemas poseían una frecuencia negativa. Por tanto, los sistemas antes mencionados necesitarían un sustrato para estabilizarse. También notamos que los cálculos antes mencionados se realizaron utilizando una celda unitaria uno por uno, y los materiales con configuración ferromagnética (FM) es el estado más estable. Sin embargo, para una supercélula más grande, encontramos que FM todavía tiene una energía menor que la configuración anti-ferromagnética (AFM) en los casos abrochados, mientras que las configuraciones FM y AFM están degeneradas en energía en los casos planos.

Conclusiones

Para resumir, nuestros cálculos de primeros principios predicen que el reemplazo de metales de transición (Ti, Zr y Hf) en películas alveolares Sb o Bi podría exhibir potencialmente la fase QAH. Aunque estos materiales son energéticamente más estables en su forma pandeada, transformarlos a una forma plana produce la fase QAH en un rango bastante razonable de constantes de celosía. Dicha fase también puede inducirse variando la distancia de pandeo y aplicando tensión como se debería en nuestros diagramas de fase calculados. Encontramos que las estructuras planas de TiBi y HfBi existen como aislantes QAH con una banda prohibida de 15 y 7 meV, respectivamente. Estos hallazgos ofrecen otra forma de realizar la fase QAH en materiales alveolares que podrían ser potencialmente útiles en aplicaciones espintrónicas.

Métodos / Experimental

Los cálculos de los primeros principios dentro del marco de la teoría funcional de la densidad (DFT) se realizaron utilizando el método de aproximación de gradiente generalizado (GGA) [32-36] y de onda aumentada de proyector (PAW) [37], tal como se implementó en la simulación Ab-Initio de Viena. Versión de paquete 5.3 (VASP) [38, 39]. El corte de energía cinética se fijó en 350 eV y las estructuras cristalinas se optimizaron hasta que las fuerzas residuales no fueran superiores a 5 × 10 ⁻³ eV / Å. El criterio de autoconsistencia para la convergencia se estableció en 10 ⁻⁶ eV para cálculos de estructuras electrónicas con o sin acoplamiento espín-órbita. Simulamos una película delgada insertando una capa de vacío de al menos 20 Å a lo largo de la z dirección en una zona de Brillouin 2D muestreada de cuadrículas Monkhorst-Pack de 24 × 24 × 1 centradas en gamma [40]. Calculamos las funciones de Wannier localizadas al máximo utilizando el paquete WANNIER90 [41] que luego se utilizaron para calcular los estados de los bordes. Las fases topológicas se identificaron calculando el número de Chern utilizando el paquete Z2Pack [42, 43] que utiliza una técnica que rastrea los centros de carga híbridos de Wannier.

Dependencia de la toxicidad de las nanopartículas en sus propiedades físicas y químicas Preparación de molienda de bolas en un solo paso de óxido de grafeno / CL-20 a nanoescala para una sensibilidad y un tamaño de partículas significativamente reducidos