Dependencia de la temperatura de picos divididos por espín en el enfoque transversal de electrones
Resumen
Presentamos los resultados experimentales de las mediciones de enfoque de electrones transversales realizadas utilizando GaAs de tipo n. En presencia de un pequeño campo magnético transversal (B ⊥ ), los electrones se enfocan desde el inyector al detector, lo que lleva a picos de enfoque periódicos en B ⊥ . Mostramos que los picos de enfoque impar exhiben una división, donde cada subpico representa una población de una rama de espín particular que emana del inyector. La dependencia de la temperatura revela que la división del pico está bien definida a baja temperatura, mientras que se difumina a alta temperatura, lo que indica que la polarización de espín impulsada por intercambio en el inyector es dominante a bajas temperaturas.
Antecedentes
El transporte de electrones a través de un sistema cuasi unidimensional (1D) realizado utilizando el gas de electrones bidimensionales (2DEG) formado en la interfaz de la heteroestructura GaAs / AlGaAs ha sido ampliamente estudiado. Un sistema 1D proporciona una plataforma excelente para imaginar no solo el sistema de mecánica cuántica sin interacción donde la cuantificación de la conductancia [1–3] está en las unidades de \ (n \ times \ frac {2e ^ {2}} {h} \ ), donde n =1,2,3 ... son diferentes sub-arenas de energía 1D, pero también un lugar para explorar la física de muchos cuerpos [4-9]. Recientemente, el progreso en la física del sistema 1D de muchos cuerpos ha ganado impulso debido a la predicción y demostración experimental de fases ricas en el sistema 1D de baja densidad que conducen a la cristalización incipiente de Wigner [6, 7, 10]. Además, el origen de la anomalía de conductancia 0,7 en el marco del sistema 1D de muchos cuerpos todavía se debate [11-15]. La anomalía 0.7 tiene dos características principales:primero, en presencia de un campo magnético en el plano, la anomalía 0.7 evoluciona hacia una meseta \ (0.5 \ times \ frac {2e ^ {2}} {h} \), lo que indica que está relacionado con el espín [4]; en segundo lugar, se encontró que la anomalía 0.7 se debilita (fortalece) con la disminución (aumento) de la temperatura [4]. Estas notables observaciones han llevado a un volumen de intentos teóricos y experimentales para sondear la polarización de espín intrínseca asociada con la anomalía 0.7; sin embargo, no existe un consenso como tal sobre el origen de esta anomalía [11-15]. Por lo tanto, para arrojar más luz sobre la anomalía 0.7, es esencial realizar una medición directa de la polarización de espín dentro de un canal 1D.
Se propuso un esquema basado en el enfoque transversal de electrones (TEF) para abordar la polarización de espín [16, 17] y se validó en GaAs de tipo p [18, 19] e InSb de tipo n [20]. Dentro de este esquema, la polarización de espín que surge de la interacción de intercambio se puede extraer de la asimetría de los dos subpicos del primer pico de enfoque. Recientemente, mostramos que la inyección de electrones 1D cuyos espines se han separado espacialmente se puede detectar en forma de una división en el primer pico de enfoque, donde los dos subpicos representan la población de estados de espín detectados [21]. En el presente trabajo, informamos la dependencia de la temperatura del primer pico de enfoque de división de espín y analizamos los resultados en función del espacio de espín presente entre las dos especies de espín.
Método
Los dispositivos estudiados en el presente trabajo se fabricaron a partir del gas de electrones bidimensionales de alta movilidad (2DEG) formado en la interfaz de GaAs / Al 0.33 Ga 0,67 Como heteroestructura. A 1,5 K, la densidad de electrones medida (movilidad) fue de 1,80 × 10 11 cm −2 (2,17 × 10 6 cm 2 V −1 s −1 ) por lo tanto, el camino libre medio es superior a 10 μ m, que es mucho mayor que la longitud de propagación del electrón. Los experimentos se realizaron en un refrigerador de dilución criogénica con una temperatura de rejilla de 20 mK utilizando la técnica estándar de bloqueo. El rango de medición de la dependencia de la temperatura fue de 20 mK a 1.8 K.
Resultados y discusión
La Figura 1 a muestra la configuración experimental junto con un espectro de enfoque típico obtenido con el dispositivo que se muestra en el recuadro. El dispositivo de enfoque está especialmente diseñado para que el inyector y el detector puedan controlarse por separado para evitar una posible intercomunicación entre ellos [21-23]. El cable cuántico utilizado para el inyector y el detector tiene un ancho (dirección de confinamiento) de 500 nm y una longitud (dirección de flujo de corriente) de 800 nm. Tanto el inyector como el detector muestran mesetas de conductancia bien definidas, como se muestra en la Fig. 1 b. Se dan más detalles sobre el dispositivo en el título de la Fig. 1.
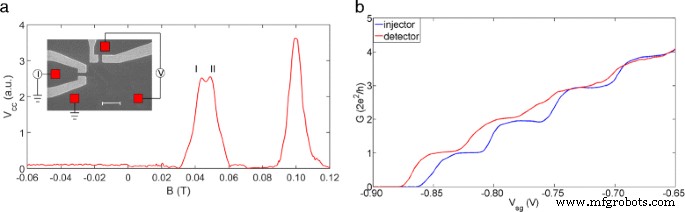
La configuración del experimento y las características del dispositivo. un Un gráfico representativo del enfoque transversal de electrones con el inyector y el detector configurados en G 0 (2e 2 / h). V cc es la caída de voltaje en el detector. Los picos de enfoque están bien definidos con un campo magnético positivo y la señal es insignificante con un campo magnético negativo. El primer pico muestra una división pronunciada. Los dos subpicos se han resaltado como pico I y pico II. El recuadro muestra una imagen SEM del dispositivo. La separación entre el inyector y el detector es de 1,5 μ metro. Los cuadrados rojos forman los contactos óhmicos, mientras que dos pares de puertas de color gris, izquierda y superior, forman el inyector y el detector, respectivamente. La barra de escala es 2 μ metro. b Características de conductancia del inyector y detector
Con un campo magnético negativo, la señal medida es casi cero porque los electrones se doblan en la dirección opuesta y, por lo tanto, pierden el detector. También es evidente que la oscilación de Shubnikov-de Haas y el efecto Hall cuántico no contribuyen a la observación. En presencia de un pequeño campo magnético transversal positivo (B ⊥ ) los electrones se enfocan desde el inyector al detector, lo que lleva a picos de enfoque periódicos en B ⊥ mientras que la señal detectada es insignificante en el extremo del campo magnético negativo. La periodicidad calculada de 60 mT usando la relación [23],
$$ B_ {foco} =\ frac {\ sqrt {2} \ hbar k_ {F}} {eL} $$ (1)está de acuerdo con el resultado experimental. Aquí, e es la carga elemental y \ (\ hbar \) es la constante de Planck reducida, L es la separación entre el inyector y el detector (en la geometría del dispositivo de enfoque de 90 °, esta es la separación a lo largo de la dirección diagonal). Además del pico de enfoque periódico que es una manifestación de la órbita del ciclotrón de electrones semiclásica, es interesante notar la división de los picos de enfoque impares. Se sugiere que esta división anómala de los picos de enfoque impares surge de la interacción espín-órbita (SOI) [16, 17] y se ha observado con éxito en el gas del agujero GaAs [18, 19] y el gas de electrones InSb [20]. Recientemente demostramos la división de picos de enfoque impares en n-GaAs [21] donde un cable cuántico más largo que posee electrones 1D parcialmente polarizados y separados espacialmente se usó para inyectar los electrones 1D polarizados en el régimen 2D y posteriormente medido a través del detector en el forma de una división en el primer pico de enfoque. Aquí, estamos interesados en investigar el efecto térmico en los estados de espín dentro del canal 1D a través del enfoque transversal de electrones. Observamos que la división se mancha cuando la energía térmica k B T excede 2 Δ E ( Δ E es la diferencia de energía entre las dos ramas de espín) de acuerdo con la predicción teórica [17].
Antes de discutir el efecto de dependencia de la temperatura, es importante comprender el mecanismo responsable de la división de picos observada. La figura 2 a, b muestra el perfil de potencial de las compuertas divididas que forman el inyector (par inferior) y el detector (par izquierdo). En presencia de SOI, las dos especies de espín siguen radios de ciclotrón diferentes como se muestra en la Fig. 2a, lo que da como resultado dos subpicos en el primer pico de enfoque. Sin embargo, la situación es diferente para el segundo pico de enfoque, donde está involucrada una dispersión en el límite del potencial electrostático creado por las puertas divididas, como se muestra en la Fig. 2 b. En este caso, un electrón de spin-up (flecha roja en las gráficas de color) sigue inicialmente un radio de ciclotrón más pequeño mientras que posee un radio más grande después de la dispersión [16, 17] y viceversa para el electrón de spin-down (flecha blanca) , por lo tanto, las dos especies de espín se vuelven a unir en el detector. El razonamiento subyacente para la división de picos se puede encontrar en el espacio k en la Fig. 2 c, d. Aquí, asumimos que la interacción espín-órbita es de tipo Rashba; sin embargo, el análisis también es válido para el efecto Dresselhaus a granel. Para el primer pico de enfoque (Fig.2 c), las dos especies de espín viajan desde (0, k y ) a (-k x , 0) a lo largo de diferentes superficies de Fermi. Para el segundo pico de enfoque (Fig. 2 d), el mismo argumento es válido antes de la dispersión; sin embargo, la cantidad de movimiento cambia de signo mientras que la orientación del giro se conserva después de la dispersión [16]. Por lo tanto, un electrón de spin-up (flechas rojas) que ocupa inicialmente la superficie interna de Fermi salta a la superficie externa de Fermi después de la dispersión para garantizar que tanto el signo del impulso como la orientación del giro estén en el orden correcto (el salto se resalta con la flecha azul gruesa en la Fig. 2 d) y viceversa para el electrón de spin-down. El radio del ciclotrón es proporcional al impulso, de modo que la alternancia en el radio del ciclotrón se produce en el espacio de coordenadas como consecuencia del salto entre dos superficies de Fermi, lo que conduce a un solo segundo pico de enfoque.
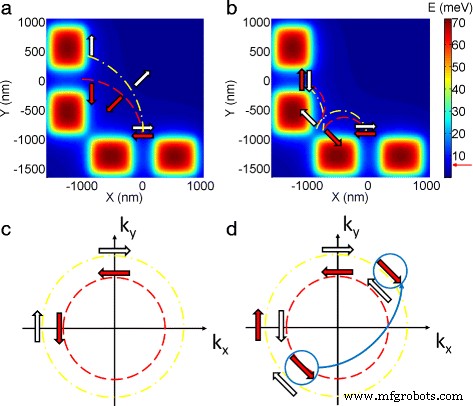
Mecanismo de división de picos. un , b División de picos en el espacio de coordenadas para el primer y segundo picos de enfoque, respectivamente. Las flechas rojas y blancas representan electrones de giro hacia arriba y hacia abajo, los bloques de colores representan el potencial electrostático y el trazo de trazo rojo es con un radio de ciclotrón más pequeño, mientras que el de puntos amarillos tiene un radio de ciclotrón más grande. c , d División de picos en el espacio k para el primer y segundo picos de enfoque, respectivamente. Los electrones viajan desde (0, k y ) a (-k x , 0) en sentido antihorario en el gráfico ( c ). En parcela ( d ), la flecha azul gruesa resalta la transición después de la reflexión en el límite del potencial electrostático formado entre el inyector y el detector
La Figura 3 a – c muestra la dependencia de la temperatura de los resultados de enfoque con el inyector configurado en 0.5G 0 , G 0 y 1.8G 0 , respectivamente, donde la temperatura de la red se incrementa de 20 mK (la temperatura del electrón está calibrada para estar alrededor de 70 mK) a 1.8 K, y la Fig. 3 d – f muestra el acercamiento de los datos en la Fig. 3 a – c , respectivamente. Para G i =0.5G 0 (Fig. 3 a) se observa un solo pico (ya que solo una subbanda de espín está ocupada), que se ensancha gradualmente a mayor temperatura. Además, el pico de enfoque se desplaza hacia el centro del espectro y se vuelve más simétrico a temperaturas más altas (ver el trazo inferior, T =1,8 K, figura 3 a, d). Esto puede deberse a una posible transición de electrones entre las dos subbandas de espín a una temperatura relativamente alta. En comparación, para G i = G 0 (Fig.3 b), los subpicos, cada uno de los cuales representa un estado de giro, están presentes desde 20 mK hasta 1.2 K. Sin embargo, la caída en el primer pico de enfoque que conduce a dos subpicos se difumina a 1.8 K ( Fig. 3 b, e). Con G i establecido en 1.8 G 0 (Fig. 3 c), la división no está bien resuelta y el subpico izquierdo (I) domina el espectro. Observamos que al aumentar la temperatura, el pico que reduje gradualmente en amplitud para dar como resultado un primer pico de enfoque asimétrico a 1.8 K. En InSb de tipo n, la división fue pronunciada incluso a 10 K, lo cual es consistente con el hecho de que el pico la división fue de alrededor de 60 mT, una indicación de un SOI fuerte en InSb [20], que es un orden más grande que la división máxima de 5,5 mT medida en el presente caso.
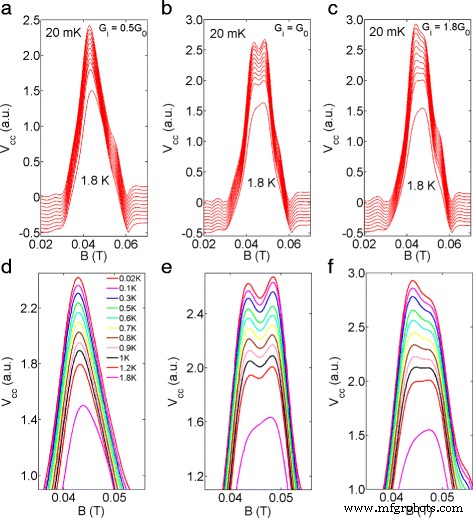
Dependencia de la temperatura de TEF. un - c El inyector se configuró en 0,5 G 0 , G 0 y 1.8G 0 , respectivamente. La temperatura de la red se incrementó de 20 mK (trazo superior) a 1,8 K (trazo inferior). Los datos se han compensado verticalmente para mayor claridad. d - f , acercamiento de los datos en ( a ) - ( c )
Para extraer el ancho y la amplitud del pico con precisión considerando que los dos subpicos pueden superponerse parcialmente entre sí, usamos dos picos de Lorentz para reconstruir los datos experimentales como se muestra en la Fig. 4a usando la relación,
$$ A (B) =\ sum \ limits_ {i =1,2} A_ {i} \ times \ frac {\ gamma_ {i} ^ {2}} {\ gamma_ {i} ^ {2} + (B -B_ {i}) ^ {2}} $$ (2)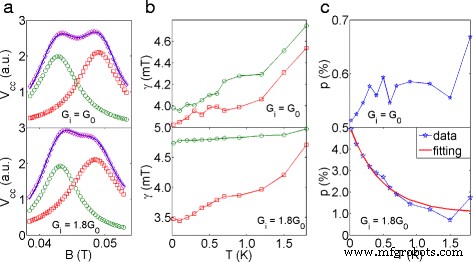
Análisis de los datos de dependencia de la temperatura. Los gráficos de la parte superior son para G i = G 0 , los de abajo son para G i =1.8 G 0 . un Reconstrucción del primer pico de enfoque con dos picos de Lorentz a 20 mK. La línea azul sólida son los datos experimentales, el marcador redondo verde es el ajuste para el pico I, el marcador cuadrado rojo es el ajuste para el pico II y el marcador de diamante magenta resalta el pico de enfoque reconstruido. b FHWM, γ en función de la temperatura:los subpicos se ensanchan al aumentar la temperatura en ambos casos. Los marcadores representan el mismo significado que en el gráfico ( a ). c La polarización medida con G i = G 0 fluctúa alrededor del 0,6 % . Por otro lado, la polarización medida con G i =1.8 G 0 sigue una caída exponencial
donde A i es la amplitud del pico i ( yo =1, 2 para el pico I y el pico II, respectivamente), γ i denota el ancho completo a la mitad del máximo (FWHM), y B i es el centro del pico. Se pueden extraer dos resultados notables del ajuste:primero, se ve en la Fig. 4 b que γ (consulte el título de la Fig.4 para obtener detalles sobre las trazas y símbolos que representan el pico I y el pico II) tanto para el pico I como para el pico II aumenta con el aumento de la temperatura independientemente de la conductancia del inyector, lo que indica que el ensanchamiento térmico de los subpicos evita la observación de división de picos a alta temperatura. Cabe señalar que el pico I para G i =1.8 G 0 es relativamente resistente a la temperatura en comparación con otros picos (ambos picos de G 0 y pico II de 1.8 G 0 ). En segundo lugar, la polarización de espín medida p \ (\ left (p =\ left | \ frac {A_ {1} -A_ {2}} {A1 + A_ {2}} \ right | \ right) \) con G i = G 0 fluctúa alrededor del 0,6 % y no muestra una dependencia explícita de la temperatura, lo que concuerda con el hecho de que la polarización del espín en la meseta de conductancia debe permanecer en 0 independientemente de la temperatura (Fig. 4 c, gráfico superior). Por otro lado, cuando G i está configurado en 1.8 G 0 , la polarización de espín extraída decae del 5 al 0,8 % (Fig. 4 d, gráfico inferior) siguiendo la relación [15],
$$ p =\ alpha exp \ left (- \ frac {k_ {B} T} {\ Delta E} \ right) + c $$ (3)donde α es un prefactor que representa la amplitud, k B es la constante de Boltzmann, Δ E es la diferencia de energía entre las dos ramas de espín y c explica el pequeño valor residual que surge de la incertidumbre en el experimento. Extrajimos el valor de Δ E estar alrededor de 0,041 meV (correspondiente a 0,5 K). La teoría [17] predice que la división debería persistir hasta k B T excede 2 Δ E (es decir, 1 K en nuestro caso), lo que concuerda razonablemente bien con nuestro resultado de que la división de picos es observable hasta 1,2 K.
Conclusión
En conclusión, mostramos la dependencia de la temperatura del enfoque transversal de electrones donde la contribución de los dos estados de espín se manifestó como dos subpicos en el primer pico de enfoque. Se observó que la división del pico está bien definida desde 20 mK hasta 1,2 K y, más allá de esta temperatura, la división del pico se extendió. Además, el pico de enfoque tiende a volverse más simétrico a temperaturas más altas, lo que indica un posible equilibrio entre las dos ramas de espín debido a la excitación térmica.
El trabajo está financiado por el Consejo de Investigación en Ingeniería y Ciencias Físicas (EPSRC), Reino Unido.
Nanomateriales



