Circuitos de resistencia-condensador en serie

En la última sección, aprendimos lo que sucedería en circuitos de CA simples de solo resistor y solo capacitor. Ahora combinaremos los dos componentes en forma de serie e investigaremos los efectos.

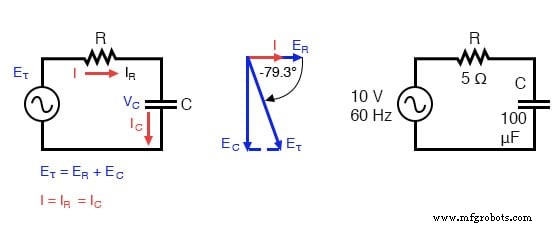
Circuito de condensadores en serie:el voltaje retrasa la corriente de 0 ° a 90 °.

Cálculo de impedancia

La resistencia ofrecerá 5 Ω de resistencia a la corriente CA independientemente de la frecuencia, mientras que el condensador ofrecerá 26,5258 Ω de reactancia a la corriente CA a 60 Hz.

Debido a que la resistencia del resistor es un número real (5 Ω ∠ 0 °, o 5 + j0 Ω), y la reactancia del capacitor es un número imaginario (26.5258 Ω ∠ -90 °, o 0 - j26.5258 Ω), el efecto combinado de los dos componentes será una oposición a la corriente igual a la suma compleja de los dos números.

El término para esta compleja oposición a la corriente es impedancia , su símbolo es Z, y también se expresa en la unidad de ohmios, al igual que la resistencia y la reactancia. En el ejemplo anterior, la impedancia total del circuito es:

La impedancia está relacionada con el voltaje y la corriente tal como cabría esperar, de manera similar a la resistencia en la Ley de Ohm:

De hecho, esta es una forma mucho más completa de la ley de Ohm que la que se enseñó en la electrónica de CC (E =IR), así como la impedancia es una expresión mucho más completa de oposición al flujo de electrones que la simple resistencia. Cualquier resistencia y reactancia, por separado o en combinación (serie / paralelo), puede y debe representarse como una sola impedancia.

Cálculo actual

Para calcular la corriente en el circuito anterior, primero debemos dar una referencia de ángulo de fase para la fuente de voltaje, que generalmente se supone que es cero. (Los ángulos de fase de impedancia resistiva y capacitiva son siempre 0 ° y -90 °, respectivamente, independientemente de los ángulos de fase dados para voltaje o corriente).

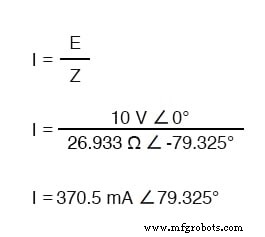
Al igual que con el circuito puramente capacitivo, la onda de corriente está liderando la onda de voltaje (de la fuente), aunque esta vez la diferencia es 79,325 ° en lugar de 90 ° completos.

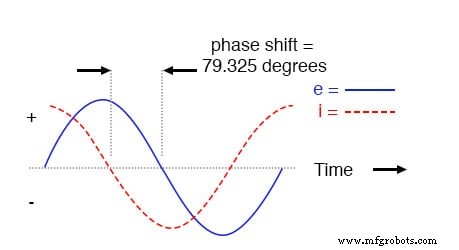
El voltaje retrasa la corriente (la corriente adelanta al voltaje) en un circuito R-C en serie.

Método de tabla

Como aprendimos en el capítulo de inductancia de CA, el método de “tabla” para organizar las cantidades de los circuitos es una herramienta muy útil para el análisis de CA al igual que lo es para el análisis de CC. Coloquemos las cifras conocidas de este circuito en serie en una tabla y continuemos el análisis con esta herramienta:

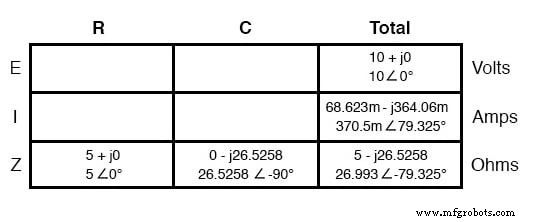
La corriente en un circuito en serie es compartida por igual por todos los componentes, por lo que las cifras colocadas en la columna "Total" para la corriente también se pueden distribuir a todas las demás columnas:

Continuando con nuestro análisis, podemos aplicar la Ley de Ohm (E =IR) verticalmente para determinar el voltaje a través del resistor y el capacitor:

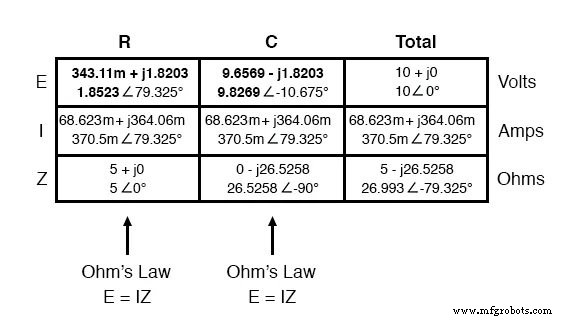
Observe cómo el voltaje a través de la resistencia tiene exactamente el mismo ángulo de fase que la corriente a través de él, lo que nos dice que E y yo estamos en fase (solo para la resistencia). El voltaje a través del capacitor tiene un ángulo de fase de -10.675 °, exactamente 90 ° menos que el ángulo de fase de la corriente del circuito. Esto nos dice que el voltaje y la corriente del capacitor todavía están desfasados ​​90 ° entre sí.

Cálculos con SPICE

Revisemos nuestros cálculos con SPICE:

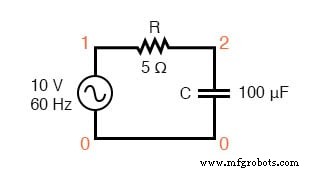
Circuito de especias:R-C.

 circuito CA r-c v1 1 0 ac 10 sin r1 1 2 5 c1 2 0 100u .ac lin 1 60 60 .imprimir ac v (1,2) v (2,0) i (v1) .print ac vp (1,2) vp (2,0) ip (v1) .fin frecuencia v (1,2) v (2) yo (v1) 6.000E + 01 1.852E + 00 9.827E + 00 3.705E-01 frecuencia vp (1,2) vp (2) ip (v1) 6.000E + 01 7.933E + 01 -1.067E + 01 -1.007E + 02 

Una vez más, SPICE imprime de manera confusa el ángulo de fase actual en un valor igual al ángulo de fase real más 180 ° (o menos 180 °).

Sin embargo, es muy sencillo corregir esta cifra y comprobar si nuestro trabajo es correcto. En este caso, la salida de -100,7 ° de SPICE para el ángulo de fase actual equivale a 79,3 ° positivo, que corresponde a nuestra cifra calculada previamente de 79,325 °.

Nuevamente, se debe enfatizar que las cifras calculadas correspondientes a las mediciones de voltaje y corriente en la vida real son aquellas en polar forma, no rectangular!

Por ejemplo, si realmente construyéramos este circuito resistor-capacitor en serie y midiéramos el voltaje a través del resistor, nuestro voltímetro indicaría 1.8523 voltios, no 343.11 milivoltios (rectangular real) o 1.8203 voltios (rectangular imaginaria).

Los instrumentos reales conectados a circuitos reales proporcionan indicaciones correspondientes a la longitud del vector (magnitud) de las cifras calculadas. Si bien la forma rectangular de la notación de números complejos es útil para realizar sumas y restas, es una forma de notación más abstracta que la polar, que por sí sola tiene correspondencia directa con las medidas verdaderas.

La impedancia (Z) de un circuito R-C en serie se puede calcular, dada la resistencia (R) y la reactancia capacitiva (X _C ). Dado que E =IR, E =IX _C , y E =IZ, la resistencia, la reactancia y la impedancia son proporcionales al voltaje, respectivamente. Por lo tanto, el diagrama de fasores de voltaje se puede reemplazar por un diagrama de impedancia similar.

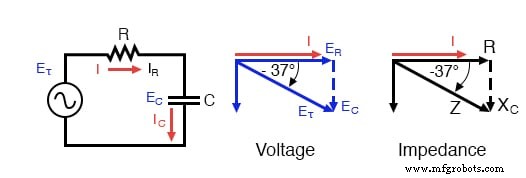
Serie:diagrama de fasor de impedancia del circuito R-C.

Ejemplo: Dado:Una resistencia de 40 Ω en serie con un capacitor de 88.42 microfaradios. Encuentre la impedancia a 60 hercios.

 XC =1 / (2πfC) XC =1 / (2π · 60 · 88,42 × 10-6) XC =30 Ω Z =R - jXC Z =40 - j30 | Z | =raíz cuadrada (402 + (-30) 2) =50 Ω ∠Z =arcotangente (-30/40) =-36,87 ° Z =40 - j30 =50∠-36,87 ° 

REVISAR:

• Impedancia es la medida total de oposición a la corriente eléctrica y es la suma compleja (vectorial) de la resistencia ("real") y la reactancia ("imaginaria").
• Las impedancias (Z) se gestionan como las resistencias (R) en el análisis de circuitos en serie:las impedancias en serie se suman para formar la impedancia total. ¡Solo asegúrese de realizar todos los cálculos en forma compleja (no escalar)! Z _Total1 + Z ₂ +. . . Z _n
• Tenga en cuenta que las impedancias siempre se suman en serie, independientemente del tipo de componentes que comprendan las impedancias. Es decir, la impedancia resistiva, la impedancia inductiva y la impedancia capacitiva deben tratarse de la misma manera matemáticamente.
• Una impedancia puramente resistiva siempre tendrá un ángulo de fase de exactamente 0 ° (Z _R =R Ω ∠ 0 °).
• Una impedancia puramente capacitiva siempre tendrá un ángulo de fase de exactamente -90 ° (Z _C =X _C Ω ∠ -90 °).
• Ley de Ohm para circuitos de CA:E =IZ; I =E / Z; Z =E / I
• Cuando las resistencias y los condensadores se mezclan en circuitos, la impedancia total tendrá un ángulo de fase entre 0 ° y -90 °.

HOJAS DE TRABAJO RELACIONADAS:

• Hoja de trabajo de circuitos de CA en serie y en paralelo