Flujo de agua de una sola fila a través de membranas nanoporosas bidimensionales
Resumen
Los avances recientes en el desarrollo de materiales bidimensionales (2D) han facilitado una amplia variedad de características químicas superficiales obtenidas al componer especies atómicas, funcionalización de poros, etc. El presente estudio se centró en cómo las características químicas como la hidrofilicidad afectan la velocidad de transporte de agua en membranas 2D hexagonales. La fuerza de la interacción entre la membrana y el agua se ajustó para cambiar la hidrofilia, y el poro subnanométrico se utilizó para investigar el flujo de una sola fila, que se sabe que retiene un excelente rechazo de la sal. Debido al comportamiento de deshumectación del poro hidrófobo, el flujo de agua fue cero o nominal por debajo del umbral de fuerza de interacción. Por encima del umbral de fuerza de interacción, el flujo de agua disminuyó con un aumento en la fuerza de interacción. A partir del potencial del análisis de fuerza media y los cálculos del coeficiente de difusión, se descubrió que la región proximal de la entrada del poro es el factor dominante que degrada el flujo de agua en el poro altamente hidrófilo. Además, la superioridad de las membranas 2D sobre las 3D parecía depender de la fuerza de la interacción. Los presentes hallazgos tendrán implicaciones en el diseño de membranas 2D para retener una alta tasa de filtración de agua.
Introducción
Se ha observado transporte de agua en una sola fila en nanoporos subnanométricos implicados en membranas sintéticas [1, 2] o membranas naturales [3, 4]. Estas formaciones de agua de una sola fila en poros subnanométricos obstaculizan eficazmente la translocación de iones al desarrollar una barrera de energía libre de deshidratación [5]. Después de encontrar tasas rápidas de flujo de agua y altas tasas de rechazo de sal en membranas de nanotubos de carbono (CNT) [2, 6], se han estudiado muchos otros factores, como la funcionalización del borde, la asignación de carga y las modificaciones de la superficie para comprender el mecanismo de transporte y aumentar la eficacia de las membranas [7,8,9,10]. Además, las membranas de óxido de grafeno se han utilizado con éxito para el tamizado de iones ajustando el espaciado entre capas de óxido de grafeno a la escala subnanométrica [11].
El descubrimiento de membranas bidimensionales (2D), iniciado por el grafeno [12], ha ganado una atención significativa en el campo de las membranas de filtración y desalinización [13]. Como resultado de su ancho de poro de un átomo de espesor, la pérdida de presión por fricción se puede minimizar teóricamente y se puede obtener un flujo de agua superior [14]. El grafeno nanoporoso de una sola capa se ha fabricado con éxito mediante el uso de un proceso de grabado con plasma de oxígeno, lo que permite controlar el tamaño de los poros [15, 16]. Se ha utilizado con éxito para membranas de desalinización al exhibir casi un 100% de rechazo de sal y un alto flujo de agua de hasta 10 6 g / m 2 s [16]. También se demuestra un alto rendimiento de desalinización mediante la realización de simulaciones de dinámica molecular (MD) [17]. Además, las membranas nanoporosas de grafeno exhibieron un tamizado molecular eficiente para la separación de gases [18, 19] y la separación de iones [15, 20].
Después de la síntesis exitosa de graphdiyne [21, 22], otros derivados del grafeno 2D como graphyne, graphone y graphane han atraído gran atención como una nueva clase de materiales 2D [23, 24]. Además, se han introducido modificaciones de la superficie que utilizan la funcionalización de poros o el dopaje químico para ampliar la funcionalidad de las membranas 2D. El dopaje con nitrógeno [25] o níquel [26] exhibió actividades catalíticas superiores. Se han incrustado éteres de corona en el nanoporo de grafeno para actividades de translocación de iones mecanosensibles [27] o translocaciones de iones selectivos [20, 28]. La funcionalización de nanoporos de grafeno utilizando nitrógeno piridínico, flúor o hidroxilo ha mostrado una mayor eficiencia de desalinización a partir de simulaciones de MD [29,30,31]. Con una porosidad naturalmente alta, graphyne-3 y graphyne-4 también demostraron ser candidatos potenciales para membranas de desalinización al demostrar una alta tasa de filtración de agua y tasa de rechazo de sal [32].
Además, materiales 2D avanzados como silicene [33], germanene [34, 35], nitruro de boro hexagonal (hBN) [36, 37] y estructuras orgánicas metálicas (MOF) [38] se han desarrollado y estudiado extensamente en los últimos años. . El desarrollo de materiales 2D se ha extendido a materiales Janus 2D estructuralmente asimétricos, como MoSSe [39, 40] e In 2 SSe [41]. Nuevos materiales 2D como MOF [42] y MoS 2 [43] han mostrado un rendimiento de desalinización eficiente utilizando simulaciones MD. En experimentos, se han sintetizado membranas MOF tan delgadas como 3 nm y se han probado para nanofiltración [44]. MoS 2 también se ha sintetizado y probado su eficacia de desalinización con un grosor de hasta 7 nm [45]. Ambos demostraron altas tasas de filtración de agua y tasas de rechazo de colorantes / sales. Se descubrió que el hBN 2D es superior a las membranas de grafeno al exhibir una mayor tasa de permeación de agua [46] de un estudio de MD.
Predecir la eficiencia de varias membranas 2D como membranas de filtración de agua requiere comprender el efecto de las propiedades químicas de la superficie en las tasas de transporte de agua. La hidrofilia de la superficie juega un papel crucial en la dinámica del agua en la interfaz [47]. En el presente estudio, la hidrofilia de la superficie se ajustó ajustando la fuerza de interacción entre la membrana y el agua y se investigó su efecto sobre el caudal de agua mediante simulaciones de MD. Para representar las membranas 2D monocapa, se seleccionó una estructura de grafeno hexagonal como estructura del modelo 2D. El flujo de agua de una sola fila a través de membranas 2D se comparó con el de las membranas tridimensionales (3D) donde las longitudes de translocación del agua corresponden a múltiples tamaños atómicos. Para representar las membranas 3D, se utilizó la estructura CNT con losas de grafeno como estructura del modelo 3D.
Métodos
Se obtuvieron membranas 2D y estructuras de membrana 3D a partir de la estructura geométrica de grafeno y nanotubos de carbono, como se muestra en la Fig. 1. Los nanoporos en membranas 2D se generaron eliminando átomos dentro de la región circular del centro del poro (designado como R2). El área de poro resultante tiene forma hexagonal donde la distancia entre los átomos más lejanos es de aproximadamente 7,52 Å. La estructura de la membrana 3D se obtuvo insertando la estructura (6,6) CNT entre dos placas de grafeno separadas 2,06 nm. Existía una ligera diferencia entre las áreas de poros de las membranas 3D y 2D. Se generó una estructura de membrana 2D adicional compuesta por un borde de CNT y una losa de grafeno para eliminar el efecto de la diferencia de tamaño de poro. La configuración se designa como R1. El radio de poro de la configuración R1 corresponde al radio de (6,6) CNT, que es 8.13 Å.
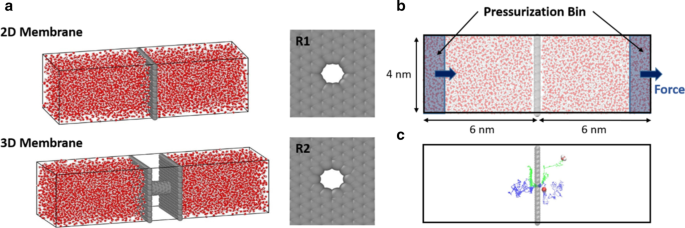
un Celdas de simulación con estructura de membrana 2D y 3D. R1 muestra una configuración de entrada de poros de la membrana 3D. Para la estructura de membrana 2D, se utilizaron las configuraciones de entrada R1 y R2. Las líneas de caja negra representan el límite periódico de las celdas de simulación. b Aplicación de fuerzas sobre moléculas de agua durante simulaciones de flujo de agua impulsadas por presión. c Trayectorias representativas de las moléculas de agua que atraviesan la membrana 2D
El tamaño plano de las membranas fue de 4,12 x 4,08 nm. El tamaño de la caja de simulación inicial fue 4.12 × 4.08 × 12 nm para simulaciones de membrana 2D y 4.12 × 4.08 × 14.06 nm para simulaciones de membrana 3D. Se aplicó una condición de límite periódica en el x , años y z direcciones junto con el cuadro de simulación, que se muestra en la Fig. 1. Las membranas se colocaron para que fueran perpendiculares a la z -dirección en el centro del cuadro de simulación ( z =6 nm). Se utilizó el modelo de agua SPC / E [48] para llenar el cuadro de simulación, ya que este modelo está de acuerdo con las propiedades de transporte experimentales como la difusividad [48, 49] y la viscosidad [50, 51]. El número total de moléculas de agua fue 6474. La interacción no ligada entre las moléculas de agua y la membrana se calculó mediante la interacción de Lennard Jones (LJ),
$$ {{V}} _ {\ rm LJ} =4 \ varepsilon \ left [{\ left (\ frac {\ sigma} {r} \ right)} ^ {12} - {\ left (\ frac {\ sigma} {r} \ right)} ^ {6} \ right] $$donde \ (\ varepsilon \) es la profundidad del pozo de potencial, \ (\ sigma \) es la distancia entre los átomos en la que el potencial es cero y r es la distancia entre átomos. En estas simulaciones, \ (\ sigma \) se fija en 0.33 nm, que es la media aritmética del parámetro de distancia de carbono y agua. La fuerza de interacción agua-membrana, \ (\ varepsilon, \) se cambia de 0.026 a 0.415 kcal / mol para ajustar la hidrofilia. Las fortalezas de interacción utilizadas en el presente estudio corresponden a 0.25 \ ({\ varepsilon} _ {0} \), 0.5 \ ({\ varepsilon} _ {0} \), \ ({\ varepsilon} _ {0} \) , 2 \ ({\ varepsilon} _ {0} \) y 4 \ ({\ varepsilon} _ {0} \), donde \ ({\ varepsilon} _ {0} \) es la fuerza de interacción LJ entre el carbono [52] y oxígeno [48].
Todas las simulaciones se realizaron utilizando el software GROMACS [53]. La integración de tiempo se realizó utilizando el algoritmo Leapfrog con un intervalo de tiempo de 1 fs. Se aplicó el termostato Nosè – Hoover [54] para mantener la temperatura a 300 K, con una constante de tiempo de 0,1 ps. El esquema de corte se utilizó para calcular la interacción LJ con la distancia de corte de 12 Å. Las interacciones electrostáticas de largo alcance se calcularon utilizando el método de malla de partículas de Ewald (PME) con un límite de espacio real de 12 Å y una cuadrícula de espacio recíproco de 1,2 Å. Durante las simulaciones de equilibrio inicial, la presión del agua normal a la membrana se ajustó a 1 bar aplicando el barostato Parrinello-Rahman [55]. Después de 1 ns de equilibrio NPT, el sistema se equilibró aún más utilizando el conjunto NVT durante 1 ns. Después de un total de 2 ns de equilibrio, se simuló el flujo impulsado por presión aplicando fuerza sobre las moléculas de agua que residen en el depósito de presurización [14, 56]. El depósito de presurización de 1 nm de longitud se encuentra al lado de la caja de simulación, como se muestra en la Fig. 1b. Las fuerzas externas que actúan sobre las moléculas de agua se calcularon mediante \ (f =\ Delta P / NA \), donde \ (\ Delta P \) es la diferencia de presión deseada a través de la membrana, N es el número de moléculas de agua en el depósito de presurización y A es el área de la membrana. Se sabe por la literatura anterior que este método es capaz de mantener muy bien la caída de presión deseada durante el curso de las simulaciones [14]. El flujo impulsado por presión se simuló durante 10 ns y los datos se recopilaron durante 9 ns después de la inicialización de 1 ns. Durante el transcurso de la simulación, las membranas se trataron como un material rígido.
Una vez realizada la simulación, se analizaron la estructura del agua y las propiedades de transporte. El coeficiente de difusión en la dirección axial de los poros se calculó mediante las relaciones de Einstein, que viene dada por
$$ {D} _ {z} =\ frac {1} {2} \ underset {t \ to \ infty} {\ mathrm {lim}} \ frac {\ langle {\ left | z \ left (t \ right ) -z (0) \ right |} ^ {2} \ rangle} {\ Delta t} $$El potencial de fuerza media (PMF) se calculó integrando las fuerzas que actúan sobre las moléculas de agua a través de las relaciones [57],
$$ \ Delta \ mathrm {PMF} =- {\ int} _ {{z} _ {0}} ^ {z} {\ rm d} {z} ^ {^ {\ prime}} \ langle F ({ z} ^ {^ {\ prime}}) \ rangle $$donde \ ({z} _ {0} \) es la ubicación del agua a granel. \ ({z} _ {0} \) =3 nm en el presente estudio. En el cálculo de ΔPMF y perfiles de coeficiente de difusión en z -dirección, se utilizaron contenedores cilíndricos con un radio de 3,8 Å a lo largo del eje del nanoporo.
Resultados y discusión
Flujo de agua
Durante la aplicación de la caída de presión a través de la membrana, se contó el número de moléculas de agua que se trasladaron a través de la membrana, como puede verse en la Fig. 2a, b. La Figura 2a, b representa el número de translocaciones de agua a través de las membranas 2D (R1) y 3D (R1), respectivamente. A partir de la pendiente de la translocación del agua frente al tiempo, se midió el flujo de agua promedio. En la Fig. 2c, se representó el flujo de agua medido con las fuerzas de interacción para las membranas 2D y 3D. A medida que aumenta la fuerza de interacción, el flujo de agua aumenta bruscamente hasta un flujo de agua máximo, y luego, disminuye monótonamente en todas las membranas. En membranas 2D, el flujo de agua de R1 fue ligeramente mayor que el de R2. La diferencia es el resultado de la región de acceso al agua algo más grande de R1.
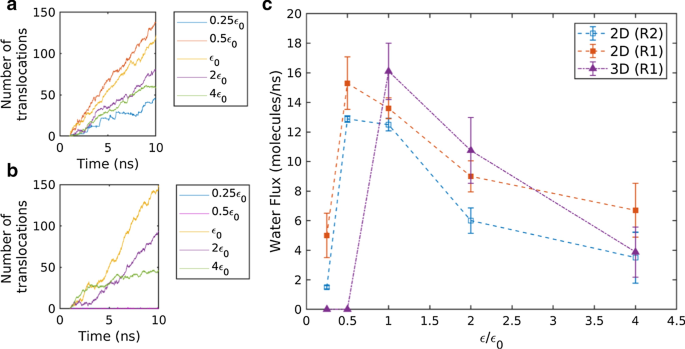
un Número de moléculas de agua translocadas con el tiempo en membranas 2D, b número de moléculas de agua translocadas con el tiempo en membranas 3D, c variación calculada del flujo de agua (número de moléculas de agua translocadas por ns) con la fuerza de interacción agua-membrana
El flujo de agua mínimo a la transición de flujo de agua máximo en la fuerza de interacción baja se debe a la transición de humectación-deshumectación de poros. En los nanoporos con un diámetro subnanométrico, las moléculas de agua están dispuestas como una cadena de una sola fila [1, 58], como puede verse en la Fig. 3e, f. El número de enlaces de hidrógeno de las moléculas de agua que forman una sola fila se reduce a aproximadamente uno y medio [59]. En la formación de la fila única, las energías de enlace de hidrógeno perdidas son parcialmente compensadas por la energía de interacción membrana-agua [1]. A una fuerza baja de interacción entre la membrana y el agua que representa el poro hidrofóbico, la interacción entre la membrana y el agua no proporciona suficiente compensación para formar la cadena de una sola fila. Este comportamiento de deshumectación se confirma tanto en las simulaciones impulsadas por la presión como en las de equilibrio, trazando el perfil de densidad y midiendo el número de ocupación (ver detalles en la sección "Densidad del agua" y la sección "Ocupación del agua en nanoporos").
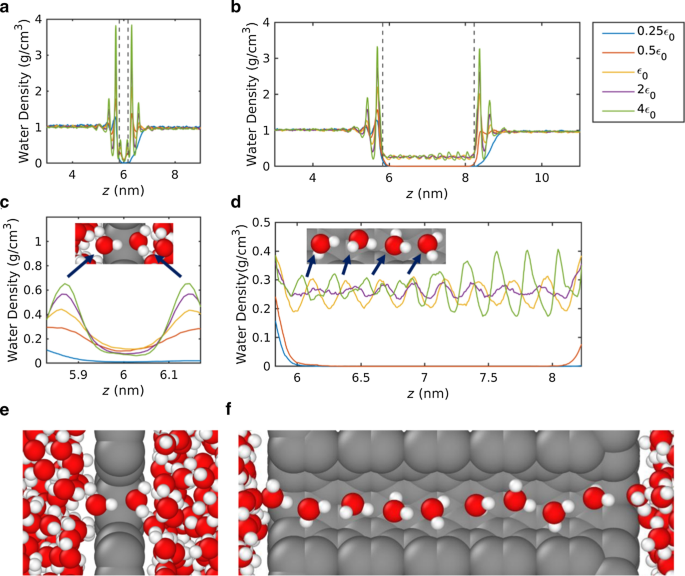
un - d Perfil de densidad del agua y e - f visualización de la formación de agua de una sola fila durante la MD. Densidad del agua a lo largo de la dirección axial del nanoporo para a Membranas 2D y b Membranas 3D. La densidad se midió en contenedores cilíndricos con un radio de poro accesible al agua. Perfil de densidad detallado dentro de la región de los poros para c Membrana 2D y d Membrana 3D. Configuración de un solo archivo dentro de la e Nanoporo 2D y f Nanoporo 3D
Las membranas 2D y 3D exhibieron diferencias en la fuerza de interacción umbral. La fuerza de interacción umbral de las membranas 3D fue mayor que la de las membranas 2D. Dentro del poro subnanométrico, una cadena parcial o moléculas de agua individuales son energéticamente desfavorables. Por lo tanto, la formación completa de la cadena dentro del poro es un requisito previo para la humectación del poro subnanométrico. Una cadena de longitud relativamente corta y baños de agua a granel ubicados muy cerca permiten humedecer las membranas 2D con una fuerza de interacción relativamente baja. Debido a tal diferencia en la fuerza de interacción del umbral, el flujo de agua de las membranas 2D fue mayor que el de la membrana 3D con fuerzas de interacción bajas (0.25 \ ({\ varepsilon} _ {0} \) y 0.5 \ ({\ varepsilon} _ {0} \)).
En el umbral de la fuerza de interacción que humedece los nanoporos, se alcanza el flujo de agua máximo. Entonces, el flujo de agua disminuye con el aumento de la fuerza de interacción. Se ha informado que las superficies hidrofóbicas promueven el deslizamiento de los límites y, posteriormente, mejoran el flujo de agua [60,61,62]. La hidrodinámica continua también gobierna el flujo de agua mejorado cuando se aplica la condición de límite de deslizamiento. La validez del mismo mecanismo en un flujo de una sola fila y la membrana 2D no está clara debido a las dimensiones subnanométricas en la dirección axial y radial de los poros. Para explicar la disminución del flujo de agua con el aumento de la hidrofilia, se investigaron la dinámica y la energía del agua (consulte las secciones "Difusividad del agua" y "Potencial de fuerza media"). Tenga en cuenta que la disminución del flujo de agua fue más significativa para las membranas 3D en comparación con las membranas 2D. Con una fuerza de interacción moderada (\ ({\ varepsilon} _ {0}, 2 {\ varepsilon} _ {0} \)), las membranas 3D son superiores a las membranas 2D, mientras que lo contrario es cierto con una fuerza de interacción alta (4 \ ( {\ varepsilon} _ {0}) \).
Densidad del agua
Los perfiles de densidad del agua a lo largo de la dirección axial de los poros se representan en la Fig. 3a – d. La densidad del agua se mide usando los contenedores cilíndricos con el radio de poro para acceder al perfil de densidad en la región de poro abierto. Las Figuras 3a yb representan el perfil de densidad del agua con membranas 2D y 3D, respectivamente, con la región de los poros indicada por las líneas discontinuas. El ancho de la región de los poros se define como el diámetro de van der Waals de los átomos de la membrana. Como el centro de los átomos de la membrana se encuentra en z =6 nm, las regiones de poros se definen como z =5,83–6,17 nm para membranas 2D y z =5,83–8,23 nm para membranas 3D. En la Fig. 3c, d, se muestra la densidad del agua dentro de la región de los poros.
En la región proximal de la entrada de los poros, se observan claramente picos y valles de densidad significativos, que representan una estructura de agua en capas. La estructura de agua en capas cerca de las paredes sólidas ha sido informada por MD [63] y estudios experimentales [64] anteriores. Como el radio de los poros es más pequeño que la distancia dentro de la cual actúan las interacciones de van der Waals (~ 1,2 nm), la estructura de agua en capas no desapareció a pesar de que el poro estaba abierto. Se observa a partir de las oscilaciones de densidad que la magnitud del pico de densidad aumenta con el aumento de la fuerza de interacción.
Los picos de densidad dentro de la región de los poros indican los sitios favorables de las moléculas de agua que forman la fila única. En los nanoporos 2D, dos picos de densidad indican que dos moléculas de agua forman un solo archivo estable. En nanoporos 3D, se observaron de ocho a nueve picos de densidad, lo que indica que se construyó una cadena de agua más larga (Fig. 3e, f). La densidad cero del agua dentro de la región de los poros indica que no penetran moléculas de agua a través de las membranas. En nanoporos 2D, la densidad del agua es cercana a cero con una fuerza de interacción de 0.25 \ ({\ varepsilon} _ {0} \); por lo tanto, el flujo de agua fue nominal para nanoporos 2D con una fuerza de interacción de 0.25 \ ({\ varepsilon} _ {0} \). En los nanoporos 3D, la densidad del agua es cero para fuerzas de interacción de 0.25 \ ({\ varepsilon} _ {0} \) y 0.5 \ ({\ varepsilon} _ {0} \), lo que significa que el flujo de agua se midió como cero para 3D nanoporos con esas fortalezas de interacción.
Ocupación de agua en nanoporos
La dinámica del agua en equilibrio también se investigó ejecutando simulaciones de equilibrio sin la diferencia de presión externa. Los números de ocupación de agua de los nanoporos se midieron contando la cantidad instantánea de moléculas de agua dentro de la región de los poros durante cada período de tiempo. La Figura 4a-l muestra el número de ocupación con el tiempo para las diversas fuerzas de interacción de las membranas 2D y 3D. Como se puede ver en la Fig. 4, la ocupación del agua demuestra la transición de los nanoporos en dos estados de llenado vacío de agua. Se sabe que esto es característico del agua de una sola fila, ya que el estado de llenado parcial (fila única rota) es energéticamente desfavorable [1]. Con una fuerza de interacción baja de 0.25 \ ({\ epsilon} _ {0} \), el estado vacío (ocupación de agua 0–1) está más poblado para las membranas 2D y 3D. Con esta fuerza, el número de ocupación promedio fue 0.37 para membranas 2D y 0.05 para membranas 3D. Con una fuerza de interacción de 0.5 \ ({\ epsilon} _ {0} \), el estado lleno (ocupación de agua 1–2) está más poblado para membranas 2D, mientras que el estado vacío todavía está poblado para membranas 3D. Con esta fuerza, el número medio de ocupación de agua fue 1,1 para las membranas 2D y 0,3 para las membranas 3D. Con una fuerza de interacción de \ ({\ epsilon} _ {0} \), el número de ocupación se completa con 8–10 para membranas 3D. Esto indica que las membranas 3D están llenas con una fuerza de interacción de \ ({\ epsilon} _ {0} \).
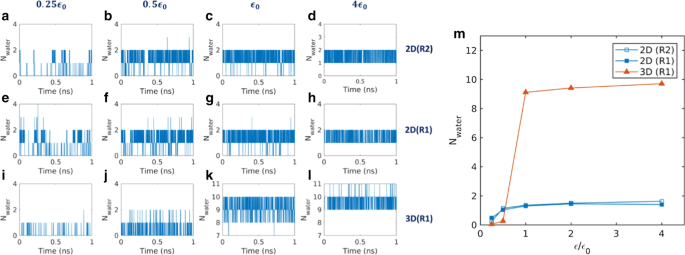
Número de ocupación de agua dentro del nanoporo para a - h 2D y i - l Membranas 3D. Las fuerzas de interacción membrana-agua son 0.25 \ ({\ epsilon} _ {0} \) para a , e y i , 0.5 \ ({\ epsilon} _ {0} \) para b , f y j , \ ({\ epsilon} _ {0} \) para c , g y k y 4 \ ({\ epsilon} _ {0} \) para d , h y l . Los números de ocupación promedio varían con la fuerza de la interacción ( m )
La variación del número de ocupación de agua promedio con la fuerza de interacción se muestra en la Fig. 4m. El comportamiento de transición de dos estados de llenado de vacío también se observó con la fuerza de interacción. Se observa claramente una transición brusca para las membranas 3D a medida que el número de ocupación salta de un número nominal a un número alto y luego aumenta ligeramente con el aumento de la fuerza de interacción. Se observa un comportamiento de transición similar en membranas 2D; sin embargo, las membranas 2D exhiben una transición moderada debido a la corta longitud de la cadena de una sola fila y al baño de agua a granel ubicado cerca, que gobiernan un estado de transición relativamente favorable.
El comportamiento de transición de los estados de llenado vacío (deshumectación-humectación) respalda la variación del flujo de agua con una fuerza de interacción baja. Por debajo del umbral de fuerza de interacción, el flujo de agua debido a la caída de presión aplicada fue cero o nominal. Con una fuerza de interacción de 0.5 \ ({\ epsilon} _ {0} \), el flujo de agua para la membrana 2D fue mucho mayor en comparación con la membrana 3D. Con esta fuerza de interacción, la membrana 2D está en estado de humectación, mientras que la membrana 3D está en estado de deshumectación. Por lo tanto, se puede concluir que la deshumectación del agua es responsable de las variaciones del flujo de agua con una fuerza de interacción baja. Desafortunadamente, la ocupación del agua no puede explicar la disminución del flujo de agua con una mayor fuerza de interacción.
Difusividad del agua
Para investigar más a fondo la dinámica del agua, se calcularon los coeficientes de difusión del agua a partir de simulaciones de equilibrio. En los perfiles de densidad, se observaron grandes oscilaciones en la región del poro proximal, lo que indica una estructura de agua en capas. La amplitud de la oscilación de la densidad aumentó con el aumento de la fuerza de interacción. Para tener en cuenta estos efectos estructurales, los coeficientes de difusión de agua en las regiones de entrada y proximidad de los poros se calcularon y se representaron en la Fig. 5a-e. La Figura 5a muestra coeficientes de difusión de moléculas de agua en diversas áreas, incluidas las regiones de proximidad y de entrada. Está claro que los coeficientes de difusión disminuyen con el aumento de la fuerza de interacción. Por lo tanto, se puede concluir que la disminución de las difusividades del agua contribuyó a la disminución del flujo de agua con el aumento de la fuerza de interacción por encima del umbral de fuerza de interacción.
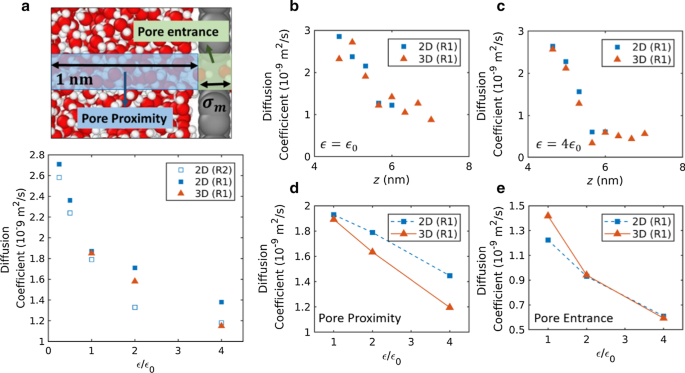
Coeficientes de difusión de agua en la proximidad de los poros y la región de entrada de los poros. La región de proximidad de los poros se define como la región cilíndrica con un radio de poro y 1 nm de longitud. La región de entrada de los poros se define como la región cilíndrica con un radio de poro y un diámetro de van der Waals. un Variaciones del coeficiente de difusión con la fuerza de interacción. Los coeficientes de difusión se miden en áreas, incluida la entrada de poros y la región de proximidad. b , c Perfil de coeficiente de difusión a lo largo de la dirección axial de los poros para una fuerza de interacción de b \ ({\ epsilon} _ {0} \) y c 4 \ ({\ epsilon} _ {0} \). d , e Variación del coeficiente de difusión con la fuerza de interacción en el d región de proximidad de poros y e región de entrada de poros
Los perfiles de los coeficientes de difusión en la dirección axial de los poros se muestran para una fuerza de interacción moderada (\ ({\ epsilon} _ {0} \)) y una fuerza de interacción alta (4 \ ({\ epsilon} _ {0} \)) en la Fig. 5b, c, respectivamente. En la Fig. 5b-e, se compara la misma configuración de poros (R1) para nanoporos 2D y 3D para eliminar cualquier efecto causado por la diferencia de configuración de poros. Se observó que los coeficientes de difusión disminuyeron gradualmente a partir de la difusividad total (~ 2.7 × 10 –9 m 2 / s [49]) mientras se acercaban a la entrada de los poros. La disminución del coeficiente de difusión puede ser consecuencia de una combinación del efecto de confinamiento de poros y el efecto de estratificación de agua. Es probable que la hidrofilia de la membrana reduzca el coeficiente de difusión mediante dos mecanismos diferentes, es decir, induciendo una estructura muy estratificada en la proximidad de los poros y aumentando la fuerza de fricción en la región de entrada de los poros. En cálculos separados del coeficiente de difusión en la proximidad de los poros y las regiones de entrada (ver Fig. 5d, e), los coeficientes de difusión disminuyeron con el aumento de la fuerza de interacción en ambas áreas.
Los coeficientes de difusión para las membranas 3D fueron ligeramente más altos o comparables a los de las membranas 2D en las regiones de entrada de los poros. Por el contrario, los coeficientes de difusión para las membranas 3D fueron más pequeños que los de las membranas 2D en la proximidad de los poros, y la diferencia es significativa en la fuerza de interacción alta (4 \ ({\ epsilon} _ {0} \)). En la simulación de flujo impulsado por presión, el flujo de agua a través de las membranas 3D exhibió una tasa de disminución más significativa con la fuerza de interacción en comparación con las membranas 2D. Esto resultó en un flujo de agua comparable o más alto para las membranas 3D con una fuerza de interacción moderada (\ ({\ epsilon} _ {0}, \) 2 \ ({\ epsilon} _ {0} \)), y un flujo de agua más alto para Membranas 2D con una alta fuerza de interacción (4 \ ({\ epsilon} _ {0} \)). Las difusividades en la proximidad de los poros parecen ser la causa principal de tal flujo de agua invertido con una alta fuerza de interacción.
Potencial de fuerza media
Para investigar más a fondo la superioridad de las membranas, que depende de la fuerza de interacción, se compararon los perfiles PMF 2D y 3D para la fuerza de interacción moderada (\ ({\ epsilon} _ {0}) \) y la fuerza de interacción alta (4 \ ({\ epsilon} _ {0} \)). Los perfiles de PMF de nanoporos 2D y 3D se comparan en la Fig. 6. El perfil de PMF muestra máximos locales, que representan la barrera de energía libre que las moléculas de agua deben superar para ser transportadas a través de las membranas. A partir de los perfiles de PMF, se identificaron dos barreras de energía de PMF importantes en la región de entrada de los poros ( z =6 nm) y la región de proximidad de los poros ( z \ (\ aprox \) 5,5 nm). Con una fuerza de interacción de \ ({\ epsilon} _ {0} \), la barrera de energía de proximidad no mostró una diferencia significativa entre 2 y 3D. Con una fuerza de interacción alta de 4 \ ({\ epsilon} _ {0} \), las barreras de energía en la proximidad aumentaron, pero con una magnitud mayor para las membranas 3D en comparación con las membranas 2D. Esto confirma que la proximidad de los poros es el factor principal para el flujo de agua invertido con una alta fuerza de interacción.
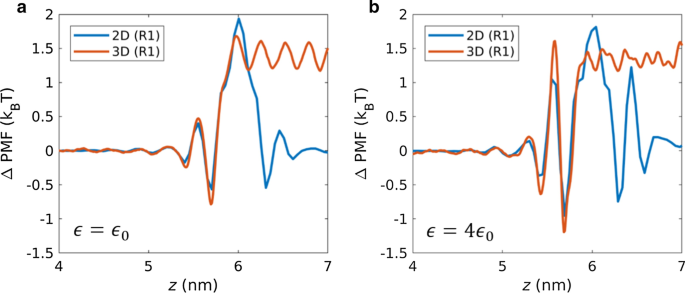
Perfiles PMF a lo largo de la dirección axial de los poros para una a fuerza de interacción moderada (\ ({\ epsilon} _ {0}) \) y b alta fuerza de interacción (\ (4 {\ epsilon} _ {0}) \)
Con el aumento en la fuerza de interacción (\ ({\ epsilon} _ {0} \) → \ (4 {\ epsilon} _ {0} \)), la barrera de energía de entrada de poros cambió de 1,94 a 1,82 para membranas 2D y 1,68 a 1,45 para membranas 3D. Hay una ligera disminución en la barrera de energía de entrada al aumentar la energía de interacción entre la membrana y el agua. Por otro lado, con un aumento en la fuerza de interacción (\ ({\ epsilon} _ {0} \) → \ (4 {\ epsilon} _ {0} \)), la barrera de energía de proximidad cambia de 0.4 a 1.05 para 2D membranas y 0,47 a 1,61 para membranas 3D. Desde el punto de vista energético, una disminución del flujo de agua con un aumento en la fuerza de interacción se debe predominantemente al aumento de la barrera de energía en la región del poro proximal. También está relacionado con la mayor reducción del flujo de agua para las membranas 3D, en comparación con las membranas 2D. La barrera de energía total para membranas 2D (2,34 k B T) es ligeramente superior a la de 3D (2,15 k B T) membranas cuando la interacción membrana-agua es moderada (\ ({\ epsilon} _ {0} \)). Debido al aumento significativo de la barrera de energía de proximidad para las membranas 3D, su barrera de energía total (3,06 k B T) es más alta que la de las membranas 2D (2,87 k B T) en el caso de una fuerza de interacción alta (4 \ ({\ epsilon} _ {0}) \). Por lo tanto, ΔPMF respalda cuantitativamente la superioridad de las membranas 2D con una fuerza de interacción alta (4 \ ({\ epsilon} _ {0}) \) y las membranas 3D con una fuerza de interacción moderada (\ ({\ epsilon} _ {0}) \).
Para el flujo de agua que no es de una sola lima a través de tamaños de poros más grandes, se presume que las membranas 2D son dominantes sobre las membranas 3D independientemente de la fuerza de interacción. El comportamiento de humectación-deshumectación con la fuerza de interacción se observó para las membranas de CNT con tamaños de poro más grandes de la literatura anterior [65]. La fuerza de interacción umbral disminuyó al aumentar el tamaño de los poros [65]. Debido a los depósitos de agua cercanos y la corta longitud de los poros, las membranas 2D exhibirán una fuerza de interacción de umbral más baja en comparación con las membranas 3D, lo que es consistente con los resultados para el flujo de una sola fila. Por lo tanto, es probable que las membranas 2D muestren un mayor flujo de agua a través de tamaños de poros más grandes en comparación con el de las membranas 3D cuando la fuerza de interacción es baja. Para una fuerza de interacción por encima del umbral, el flujo de agua a través de las membranas 2D aún puede ser mayor que el de las membranas 3D en comparación con el flujo de agua de una sola fila. La barrera de energía PMF en la proximidad de los poros no afectará tanto el flujo de agua, y las fricciones entre la pared de la membrana y la molécula de agua se convertirán en un factor dominante que afectará el flujo de agua. En la literatura anterior se ha informado de que el flujo de agua a través de las membranas de CNT aumenta con la disminución de la longitud de CNT para el flujo que no es de una sola fila [66, 67]. Además, para el flujo que no es de una sola fila, se observó un mayor flujo de agua a través de las membranas de grafeno en comparación con el de las membranas de CNT [14].
Conclusiones
In the present study, the effect of the membrane–water interaction strength on the single-file water flux was investigated. Due to the recent advances in two-dimensional membranes, hexagonal 2D membrane structures were considered and compared with the 3D tube type structure. The main observations are as follows:(1) water flux is zero or nominal below the threshold interaction strength, (2) the threshold interaction strength is lower for 2D membranes compared with 3D membranes, (3) water flux decreases with increase in interaction strength when the interaction strength is larger than the threshold interaction strength, and (4) the decrease in water flux was more significant for 3D membranes compared with 2D membranes.
The zero or nominal flux at a low interaction strength was due to the dewetting behavior, which was supported by the small occupation number and water density inside the pore. Above the threshold interaction strength wetting the pore, the water flux decreases with increase in interaction strength. The increase in the interaction strength resulted in an increased PMF energy barrier and decreased diffusion coefficients at the pore proximity, consequently reducing the water flux. In addition, the water structure and dynamics in the pore proximity were more affected by the interaction strength in the 3D membrane compared with that of the 2D membrane. It resulted in the higher reduction of water flux for 3D membranes, compared with the 2D membranes.
Due to the complicated single-file flux dependency on the interaction strength and membrane dimensions, the superiority of 2D membranes over 3D membranes appears to depend on the interaction strength. For a moderate interaction strength (l \({\epsilon }_{0}\),\({2\epsilon }_{0})\), the 3D membrane shows a slightly higher water flux compared with the 2D membranes. For a low (0.5\({\epsilon }_{0}\)) and high interaction strength (4\({\epsilon }_{0}\)), the 2D membrane shows a higher water flux than the 3D membranes. To conclude, the superiority of 2D membranes over 3D membranes depends on the membrane hydrophilicity due to the wetting–dewetting transition and diffusion dynamics in pore proximity. The present findings will be useful in the design and manipulation of 2D membranes to retain a high filtration flux.
Disponibilidad de datos y materiales
The datasets supporting the conclusions of this article are included within the article, and further information about the data is available from the corresponding author on reasonable request.
Abreviaturas
- 2D:
-
Dos dimensiones
- 3D:
-
Tridimensional
- CNT:
-
Nanotubos de carbono
- MD:
-
Dinámica molecular
- hBN:
-
Nitruro de boro hexagonal
- MOF:
-
Metal organic framework
- LJ:
-
Lennard–Jones
- PMF:
-
Potential of mean force
Nanomateriales
- Aspersor para césped
- Lavavajillas
- Pistola de agua
- Inodoro
- Boca de incendios
- Agua
- Champú
- Panel de yeso
- Los científicos de IBM miden la transferencia de calor a través de átomos individuales
- La nueva tecnología de filtración mejora la purificación de aguas residuales y la hace energéticamente eficiente
- ¿Qué es un Bibcock?



