Impedancia de superficie de estructuras híbridas de grafeno / metauperficies

Métodos

Impedancias para parches cuadrados y hojas de grafeno

En la figura 1a se presenta una estructura común de un absorbente de metasuperficie-grafeno. Este absorbente de estructura simple se puede fabricar fácilmente mediante micromecanizado de superficie. En esta configuración, una fina capa híbrida conductora de metasuperficie-grafeno y el plano de tierra metálico están separados por un sustrato dieléctrico como espaciador. La distancia al suelo es h . Para un parche cuadrado de tamaño pequeño en comparación con la longitud de onda (período de la matriz D ≪ λ ) y los parches están separados por ranuras estrechas (ancho de la ranura D - w ≪ D ), el modelo actual es válido. De acuerdo con la teoría de la línea de transmisión, se puede construir un modelo de circuito equivalente de la estructura absorbente (que se muestra en la Fig. 1b), que puede modelar la metasuperficie-grafeno. Una línea de transmisión, cortocircuito y la impedancia de la red Z _mg , respectivamente, modele la sección del sustrato dieléctrico, el plano de tierra y la impedancia de la superficie de la capa híbrida con patrón superior. Según la teoría de la línea de transmisión, la impedancia de entrada Z _en de este absorbedor se puede establecer de la siguiente manera:

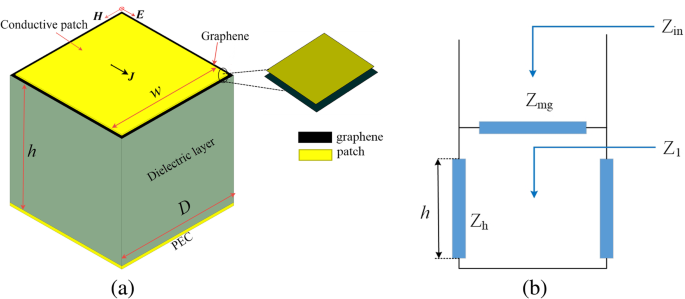
un Esquema de la celda unitaria absorbente de metasuperficie-grafeno. b Modelo de circuito equivalente local

Donde Z _h y k _zh son la impedancia de las capas de sustrato y la constante de propagación en esta región, respectivamente. Entonces, la absortividad a la incidencia normal se puede calcular mediante

Es obvio que la impedancia de la hoja de metasuperficie-grafeno se puede extraer del coeficiente de reflexión simulado. La relación entre el tamaño del parche conductor y el potencial químico μ _c se puede encontrar.

Impedancia para parches cuadrados

Cuando la onda plana es perpendicular a la metasuperficie, la matriz de parches planos actúa como una cuadrícula capacitiva (como se muestra en la Fig. 1a). Impedancia de superficie Z _m se puede ilustrar como las propiedades electromagnéticas de parches cuadrados que relacionan la intensidad de corriente promedio 〈 J 〉 Y la intensidad del campo eléctrico promedio 〈 E 〉 En el plano del parche:

En el caso de una impedancia de lámina resistiva pura con pérdidas Z _s (soy Z _s =0), con una incidencia normal, la impedancia equivalente del parche está representada por Z _m , y se puede expresar de la siguiente manera [9, 18]:

Donde \ ({\ eta} _ {\ mathrm {eff} =} \ sqrt {\ mu_0 / {\ varepsilon} _0 {\ varepsilon} _ {\ mathrm {eff}}} \) representa la impedancia de onda del host uniforme medio y D / w es el elemento geométrico. La permitividad relativa efectiva se puede aproximar como

Además, el parámetro de cuadrícula α para una matriz eléctricamente densa de parches idealmente conductores se puede escribir como

\ ({k} _ {\ mathrm {eff}} ={k} _0 \ sqrt {\ varepsilon _ {\ mathrm {eff}}} \) es el número de onda en el medio de host efectivo. En el espacio libre, μ ₀ , ε ₀ y k ₀ son la permeabilidad, la permitividad y el número de onda, respectivamente. Además, vale la pena señalar que la relación (4) es válida cuando la longitud de onda λ es mucho mayor que D .

De acuerdo con la ecuación (2), podemos encontrar que la impedancia equivalente no solo está determinada por la resistividad de la hoja de material, sino también por el período de la matriz D y ancho w de los parámetros de la estructura. Para verificar la certeza de tales fórmulas analíticas, los resultados obtenidos por las simulaciones de onda completa se presentan y comparan con las soluciones analíticas. La simulación discutida aquí se realizó utilizando el software Ansoft HFSS disponible comercialmente. Para obtener las características de reflexión de la celda unidad absorbente de meta-superficie-grafeno, se implementaron las condiciones de contorno periódicas y los puertos Floquet. Durante su simulación, la impedancia de la hoja resistiva pura con Z _s =35 Ω / sq se deposita sobre el sustrato con espesor h =20 μm, longitud D =20 μm, y la permitividad relativa de ε _r =3.2 (1 - j 0,045). Para extraer la impedancia del parche Z _m , según la relación entre la impedancia de entrada simulada Z _en y la impedancia de la superficie de la placa dieléctrica conectada a tierra Z _{g d} , la impedancia del parche de metasuperficie se puede expresar de la siguiente manera:

Donde Z _gd = jZ _d bronceado ( k _d h ), \ ({Z} _d =\ sqrt {\ mu_0 / {\ varepsilon} _0 {\ varepsilon} _r} \) es la impedancia característica de la losa, \ ({k} _d =\ omega \ sqrt {\ mu_0 {\ varepsilon} _0 {\ varepsilon} _r} \) es la constante de propagación ortogonal a la superficie del sustrato para el modo TEM.

Los resultados analíticos se verifican por comparación con los simulados basados ​​en el coeficiente de reflexión extraído, como se muestra en la Fig. 2. Las curvas negras muestran los resultados simulados mientras que las curvas rojas se calculan utilizando la expresión analítica propuesta. Aunque existe una pequeña diferencia entre los resultados simulados y las predicciones teóricas, esto se debe a la ecuación. (3) es una ecuación aproximada. La tendencia general es la misma. Por lo tanto, confirmando la validez y precisión de nuestra expresión analítica para este modelo.

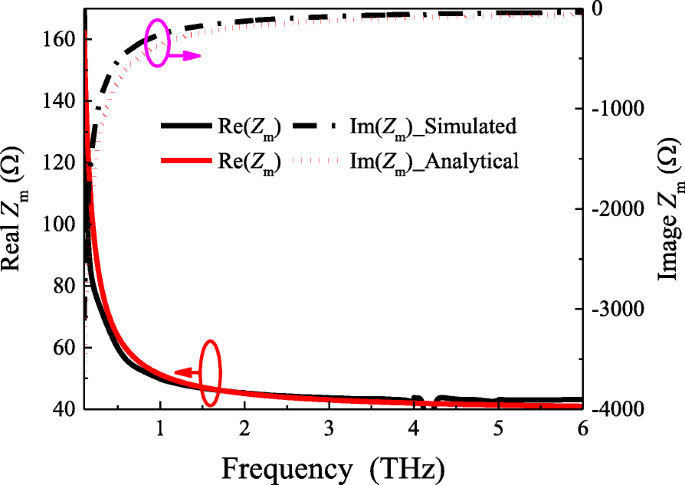
Impedancias de cuadrícula analíticas y simuladas de la matriz de parches con w =19 micras

Para investigar el efecto de los tamaños de parche en la impedancia Z _m y validar la efectividad de la fórmula (2), realizamos la simulación numérica adicional. La Figura 3 traza las partes real e imaginaria de la impedancia de la red Z _m para varios parámetros geométricos de la celda unitaria. De la Fig. 3a, se puede observar que las partes reales de la impedancia Z _m disminuye a medida que el parámetro w aumenta de 17 a 19,5 μm. De acuerdo con la Ec. 2, podemos encontrar que las partes reales de Z _m son inversamente proporcionales a la longitud del parche w . Sin embargo, las partes imaginarias muestran la tendencia opuesta como se muestra en las líneas de puntos (que se muestran en la Fig. 3b). Teniendo en cuenta las Ecs. (2) y (3), las partes imaginarias pueden estar dadas por

$$ w \ propto \ ln \ left (\ mathit {\ sin} \ frac {\ pi w} {2D} \ right) \ propto \ frac {1} {\ alpha} \ propto \ operatorname {Im} \ left ( {Z} _m \ right) $$ (8)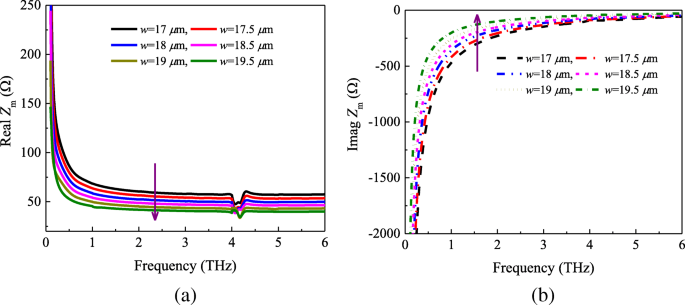

un Real y b parte imaginaria de la impedancia Z _m con diferentes tamaños del parche

De la relación (8), sabemos que cuando w aumenta de 17 a 19,5 μm, las partes imaginarias de la impedancia Z _m aumentará.

Impedancia para hojas de grafeno

El grafeno puede verse como una superficie infinitesimalmente delgada. Cuando no hay polarización magnetostática externa ni dispersión espacial, la conductividad superficial σ _g , se puede calcular con [29]

$$ {\ sigma} _ {\ mathrm {g}} =\ frac {j {e} ^ 2 {k} _BT} {\ pi {\ mathrm {\ hslash}} ^ 2 \ left (\ omega + j / \ tau \ right)} \ left [\ frac {\ mu_c} {k_BT} +2 \ ln \ left ({e} ^ {- {\ mu} _c / {k} _BT} +1 \ right) \ right] + \ frac {j {e} ^ 2} {4 \ pi \ mathrm {\ hslash}} \ ln \ left [\ frac {2 \ left | {\ mu} _c \ right | - \ left (\ omega + j / \ tau \ right) \ mathrm {\ hslash}} {2 \ left | {\ mu} _c \ right | + \ left (\ omega + j / \ tau \ right) \ mathrm {\ hslash}} \ right] $$ (9)

Donde ℏ es la constante de Planck reducida, e es la carga de un electrón, k _B es la constante de Boltzmann, mientras que μ _c , ω , τ y T son el potencial químico, la frecuencia angular, el tiempo de relajación y la temperatura, respectivamente. Aquí, asumimos T =300 K y τ =0,1 ps a lo largo de este estudio. La impedancia de la hoja de grafeno se puede calcular como

$$ {Z} _g \ left ({\ mu} _c \ right) =1 / {\ sigma} _g ={R} _g \ left ({\ mu} _c \ right) + j {X} _g \ left ( {\ mu} _c \ right) $$ (10)

Donde R _g y X _g son la resistencia superficial y la reactancia.

La impedancia de la hoja de grafeno se calcula de acuerdo con las Ecs. (9) y (10). La figura 4 indica los componentes reales e imaginarios de la impedancia de la superficie frente a la química μ _c . Podemos encontrar que la resistencia de la superficie y la reactancia disminuyen continuamente al aumentar μ _c . Además, las partes reales de la resistencia de la superficie de la hoja de grafeno se mantienen casi sin cambios en el rango de 0,2 a 6 THz cuando el potencial químico se fija en un cierto valor.

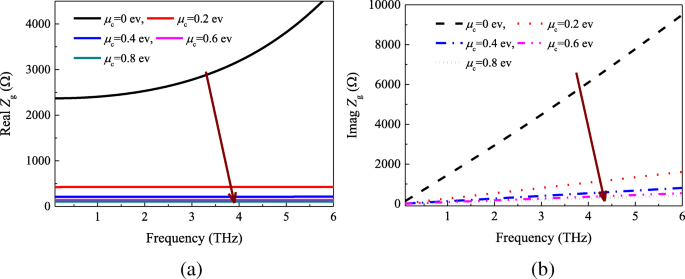
un Real y b partes imaginarias de la impedancia de la superficie en función de la frecuencia y el potencial químico

Resultados y discusión

En el caso de un parche cuadrado en una hoja de grafeno, se debe determinar la impedancia de la superficie para esta estructura híbrida. En la literatura anterior [8, 30,31,32,33,34,35,36,37], la impedancia total en la superficie de esta estructura híbrida Z _mg es igual a la combinación en paralelo de la impedancia del parche cuadrado Z _m y la impedancia de la hoja de grafeno Z _g , es decir, Z _mg = Z _m ∥ Z _g . Sin embargo, a través de nuestra simulación y cálculo, se encuentra que esta relación no es válida. Para verificar la autenticidad, simulamos una unidad absorbente de metasuperficie-grafeno que se muestra en la Fig. 1a, luego recuperamos la impedancia de la superficie de la película de acuerdo con la Eq (1). La Figura 5 muestra los valores analíticos y simulados de la parte real e imaginaria de Z _mg a diferentes potenciales químicos con w =19 μm.

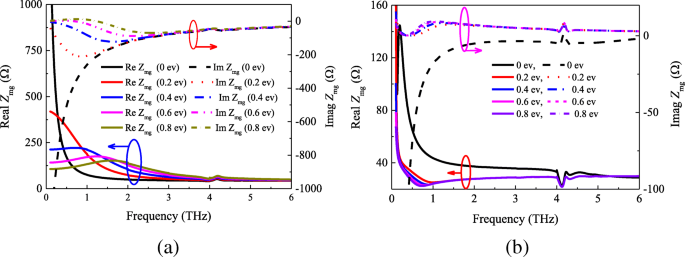
Impedancia de película de meta-superficie-grafeno Z _mg con diferentes potenciales químicos. un Analítica y b resultados simulados

De la Fig. 5a, b, se puede ver que existen grandes diferencias entre los resultados analíticos y simulados. La Figura 5a muestra que la parte real de los resultados analíticos se concentró principalmente entre 40 y 500 Ω, y la parte imaginaria de la impedancia efectiva oscila entre - 210 y 0 Ω. Sin embargo, de acuerdo con la Fig. 5b, podemos encontrar que los valores de la parte real de impedancia de 20 a 140 Ω, y la parte imaginaria se acercan a 0 al aumentar μ _c de 0 a 0,8 ev. Sin embargo, los resultados analíticos y simulados muestran la misma tendencia de que la impedancia tenderá a ser estable al aumentar la frecuencia. La razón es que las impedancias de la hoja de grafeno y el parche cuadrado se vuelven más pequeñas cuando aumenta la frecuencia. Es de destacar que, comparando la impedancia de la película de metasuperficie-grafeno a 0 ev con los otros resultados, la impedancia Z _mg es bastante diferente. Esto se debe a que los valores de la impedancia de la hoja de grafeno a 0 ev son bastante diferentes del potencial químico más alto (visto en la Fig. 4).

Por lo tanto, podemos sacar las siguientes conclusiones a partir de la impedancia calculada y simulada en la Fig. 5. Primero, la impedancia de la superficie de la película de metasuperficie-grafeno Z _mg no es estrictamente igual a la combinación paralela de Z _m y Z _g . Sin embargo, en segundo lugar, existe una cierta relación entre ellos. Para demostrar estas conclusiones, primero simulamos la estructura del absorbente que se muestra en la Fig. 1 con diferentes tamaños de parche. El coeficiente de reflexión del absorbedor de metasuperficie-grafeno con el potencial químico μ _c =0.4 ev se muestra en la Fig. 6. De acuerdo con la teoría y el modelo de la línea de transmisión, la impedancia Z _mg Puede ser obtenido. La Figura 7 muestra los componentes reales e imaginarios de la impedancia recuperada Z _mg con diferentes tamaños de parche. Según la Fig. 7a, se puede ver que la parte real de la película de metasuperficie-grafeno disminuye al principio a medida que la longitud del parche w aumenta de 17 μm a 19,5 μm. Sin embargo, se encuentra la tendencia opuesta cuando la frecuencia es superior a 0,31 THz. Por otro lado, la Fig. 7b indica que la tendencia de la parte imaginaria es la misma que la de la primera mitad de la Fig. 7a. Además, comparando las Figs. 4 y 5a, encontramos que había una situación similar en las Figs. 3 y 7. También prueba directamente las conclusiones anteriores.

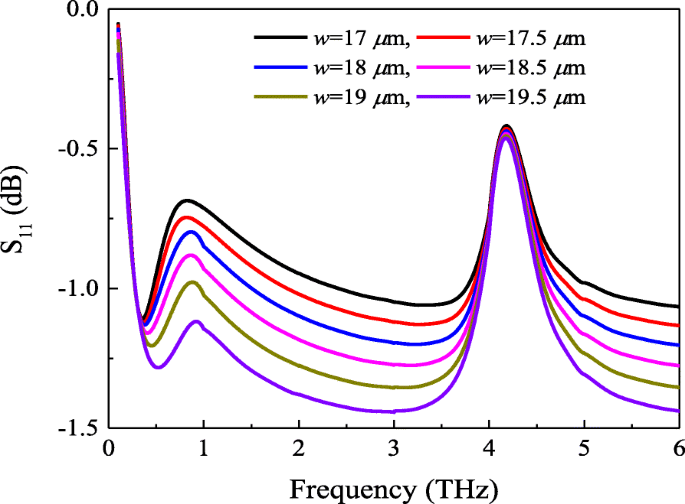
Coeficiente de reflexión del absorbedor de metasuperficie-grafeno con el potencial químico μ _c =0,4 ev

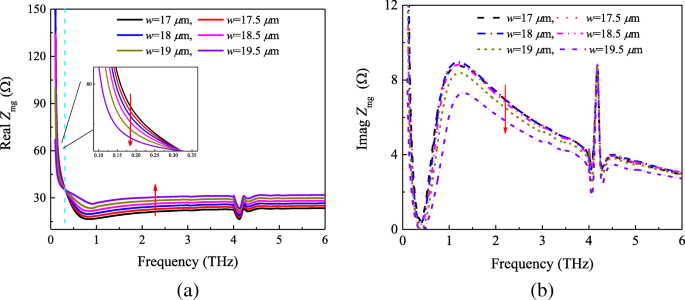
Impedancia de película de meta-superficie-grafeno Z _mg recuperado de S -parámetros con potencial químico μ _c =0,4 ev. un Real y b partes imaginarias

Para explorar más a fondo los orígenes físicos de la resistencia de la superficie en función del tamaño del parche, se investigan las distribuciones de corriente superficial de la película de metasuperficie-grafeno en incidencia normal a 3 THz. La Figura 8 muestra la variación en la intensidad de la corriente para w =17, 18 y 19 μm con el potencial químico μ _c =0.4ev. El color representa la intensidad del campo. Obviamente, a medida que aumenta el tamaño, la magnitud de la corriente superficial disminuye. Teniendo en cuenta la ecuación. 3 y la Fig. 7a, cuando la intensidad del campo eléctrico es un valor fijo en 3 THz, la impedancia de la película de metasuperficie-grafeno puede estar dada por

$$ {Z} _ {mg} \ propto w \ propto \ frac {1} {J} \ kern0.5em \ left (f> 0.32 \ \ mathrm {THz} \ right) $$ (11)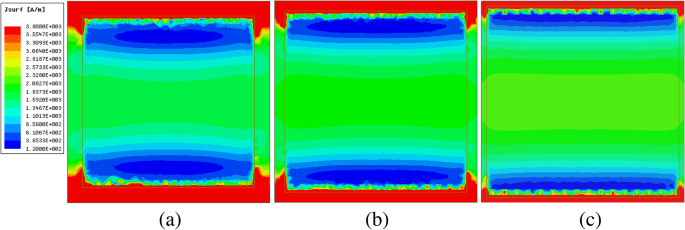

Magnitud de la corriente superficial con diferentes tamaños de parche pero a la misma frecuencia. un w =17 micras, b w =18 μm y c w =19 micras

De la relación (11), podemos encontrar que la longitud del parche es inversamente proporcional a la magnitud de la corriente superficial J . Se puede observar claramente la concordancia cualitativa entre los resultados simulados y teóricos. Para analizar cuantificablemente este fenómeno físico, el valor integral de la distribución de corriente superficial en la película de metasuperficie-grafeno se calcula utilizando la calculadora de campos HFSS, y los valores son 1.10e-6, 1.07e-6 y 1.04e-6 A , respectivamente. Estos resultados son consistentes con la Fig. 8.

Conclusiones

En resumen, para la película delgada de metasuperficie-grafeno en frecuencia THz, se investigaron las impedancias superficiales fundamentales y efectivas. Se derivaron y verificaron fórmulas analíticas para calcular la impedancia de un parche cuadrado. En cuanto a la estructura híbrida de metasuperficie-grafeno, los resultados simulados basados ​​en el coeficiente de reflexión extraído se compararon con los resultados analíticos obtenidos de la combinación paralela del parche cuadrado y las impedancias de la hoja de grafeno. Se realizó un análisis adicional al discutir el efecto del tamaño del parche sobre la impedancia efectiva. Además, las relaciones entre el tamaño del parche y la impedancia de la película se explicaron cualitativa y cuantificativamente trazando e integrando la corriente superficial. Este método de análisis se puede ampliar para estudiar el problema de impedancia con otras dos capas conductoras diferentes. Además, la simulación numérica extensiva, así como la optimización analítica de capas compuestas para aplicaciones especialmente aplicadas a la antena y al absorbedor, pueden evitarse mediante nuestro análisis realizado en este trabajo.

Abreviaturas

HFSS:

Simulación de estructura de alta frecuencia

TEM:

Electromagnético transversal

THz:

Terahercios

Uso de nanopartículas magnéticas cargadas positivamente para capturar bacterias a concentraciones ultrabajas Entrega de ARNip catiónico basado en micelas para una terapia génica eficaz contra el cáncer de colon